Myron G. Best. Igneous and metamorphic 2003 Blackwell Science

Подождите немного. Документ загружается.

UNDAMENTAL

UESTIONS

ONSIDERED IN

HIS

HAPTER

1. How are crystal-melt equilibria portrayed in phase

diagrams?

2. What do phase diagrams tell about crystallization

and melting in magma-rock systems as intensive

variables change?

3. How are chemical variations created in evolving

melts and in associated crystalline products during

crystallization of magmas?

4. How do stabilities of major rock-forming minerals

depend on intensive variables in magmas?

INTRODUCTION

Knowledge of the nature of chemical interactions be-

tween coexisting melt and crystals in magmas as inten-

sive parameters change is essential to an understanding

of how magmas are generated from solid rock at their

sources, how magmas evolve and crystallize during as-

cent and cooling, and how the composition of an ig-

neous rock can provide information on these parame-

ters. This chapter deals with equilibrium relations

between major rock-forming minerals and their associ-

ated melts in simple model and more complex multi-

component systems under controlled conditions. Such

equilibria indicate what is possible and impossible in

real magmas and serve as guides for their behavior.

Crystal-melt equilibria are represented in phase dia-

grams that have been determined in the laboratory for

hundreds of systems of a wide range of composition at

crustal and upper mantle pressures and temperatures.

Useful summaries and discussions of phase diagrams

and crystal-melt equilibria can be found in Ernst

(1976), Morse (1980), and Hess (1989).

5.1 PHASE DIAGRAMS

Phase diagrams were introduced in Section 3.3 as

graphical models that portray states of stable equilib-

rium in terms of the intensive variables P, T, and X.

Though not explicitly shown, any phase diagram im-

plies the following (Figure 3.7):

1. A stable state represented in a stability ﬁeld has the

lowest possible Gibbs free energy or chemical po-

tential for the values of the intensive variables de-

lineating the ﬁeld.

2. A boundary line between stability ﬁelds of differ-

ent phases is the locus of points representing in-

tensive parameters for which the phases are in

equilibrium.

Because of experimental constraints and the limita-

tions of a two-dimensional page of paper, phase dia-

grams generally portray only two variables, either P-T,

P-X, or T-X. Three or more variables can be repre-

sented in special projections.

5.1.1 Phase Rule

A useful formulation that aids in the interpretation of

phase diagrams is the phase rule, which provides an in-

ventory of the number of phases, components, and de-

grees of freedom in a system at equilibrium. For deﬁn-

itions and examples of phases refer to Sections 3.3 and

Figure 4.1 and for components Section 3.4.1. The de-

grees of freedom, or the variance, of a system is the

number of independent intensive variables that must be

speciﬁed to characterize the state of equilibrium fully.

CHAPTER

Crystal-Melt

Equilibria in

Magmatic Systems

A phase rule can easily be formulated for a system

of only one component, C  1, such as the silica sys-

tem shown in P-T space in Figure 5.1. In this one-

component system, as in most two-dimensional phase

diagrams, the areas, lines, and points have special sig-

niﬁcance and meaning, as follows:

1. Stability ﬁelds are areas over which a phase or as-

semblage of phases is stable.

2. Equilibrium boundary lines lie between stability

ﬁelds and represent values of intensive variables

where phases in adjacent stability ﬁelds coexist

stably.

3. Triple points are where equilibrium boundary lines

meet. All phases in adjacent stability ﬁelds coexist

in equilibrium.

Note the descending dimensionality—2, 1, and 0—of

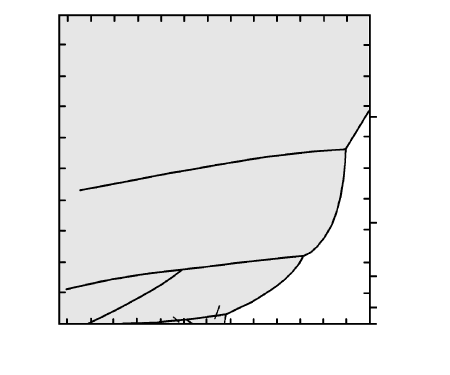
these three geometric elements. In Figure 5.1, one crys-

talline phase, such as -quartz, has the lowest possible

Gibbs free energy of any polymorph for the range of P

and T within its labeled ﬁeld. In this one-phase ﬁeld of

-quartz, both P and T can be varied independently

over a range of values without affecting the state of

equilibrium or the stability of -quartz. Therefore, in

this one-phase stability ﬁeld the state of equilibrium is

divariant, or has two degrees of freedom, F  2. Al-

though stable throughout this ﬁeld, the properties of

the -quartz, such as its exact density, vary slightly with

respect to P and T. Along any boundary line between

their individual stability ﬁelds, two phases, say, liquid

and coesite, are in equilibrium. Their free energies are

equal. Only one variable, P or T, may be independently

changed along a boundary line representing the equi-

librium between the two phases. In selecting an arbi-

trary value for P, say, 60 kbar, there is no freedom in

what T may be: It is 2650°C. For the free choice of the

value of one intensive variable, P, then, T is uniquely

ﬁxed, or vice versa. This equilibrium is univariant, or

the degrees of freedom, F  1. Where three phases co-

exist in equilibrium at a triple point, say, at just over

2400°C and about 44 kbar, where liquid, coesite, and

-quartz coexist, the equilibrium is invariant: there are

no degrees of freedom F  0; there is no freedom in

either P or T; they are unique for the three-phase equi-

librium of liquid, coesite, and -quartz. In summary, it

appears the phase rule for a one-component system is

F  3 where  is the number of phases present;

for each additional phase coexisting in equilibrium, the

variance of the system decreases by 1.

In formulating a phase rule for multicomponent sys-

tems at equilibrium, we ﬁrst take an inventory of the

number of possible variables. These are generally P, T,

and X. If other factors inﬂuence states of equilibrium,

they must be added to the list. The composition of each

equilibrium phase is denoted by the mole fractions of

its components, X

, X

. . . (Section 3.4.1). But

as the sum of these mole fractions is 1, we actually only

have (C  1) independent mole fractions as variables

for each phase, where C is the number of components.

So, if the total number of phases is , then the total

number of compositional variables is (C  1). There-

fore, the overall total number of possible variables in

the system at equilibrium is 2 (C  1), where the

2 represents P and T.

We next consider how many relations or equations

exist to evaluate the 2 (C  1) variables in the sys-

tem. At equilibrium, the chemical potential of a partic-

ular component, i, must be the same in every phase,

a, b, c, . . . in the system in which the component oc-

curs, or





 ···

and similarly for component j





 ···

and so on, for each component. Hence, for each com-

ponent there are 1 equations, and for the entire

system, C(1) equations. These C(1) equations

reduce the number of total variables so that the vari-

ance of the system, that is, the difference between the

number of possible variables and the equations deﬁn-

ing them, is

5.1 F  [2 (C  1)]  [C(1)] or

F  2  C 

This is the Gibbs phase rule. For a one-component

system the phase rule becomes F  2  1 3 

, as earlier. Remember that the number 2 in the phase

rule refers to the variables P and T. If P (or T ) is ﬁxed,

or constant, then the phase rule becomes F  1 

C , and if both P and T are ﬁxed, then F  C .

88 Igneous and Metamorphic Petrology

400 800 1200

1600

2000 2400 2800

P (GPa = 10 kbar)

T (°C)

100

200

400

Depth (km)

Stishovite

Coesite

Cristobalite

Tridymite

LIQUID

-Quartz

5.1 One-component silica phase diagram. Stability ﬁelds of crys-

talline polymorphs are shaded. (Redrawn from Swamy et al.,

1994.)

The phase rule tells us the maximum number of in-

tensive variables, F, that may independently vary with-

out changing the number of phases, , in a system of C

components at equilibrium. A knowledge of the phases

present at equilibrium is necessary to determine C and

to apply the rule, from which the variance can then be

determined. For example, as a result of the metastable

persistence of some phase into the stability ﬁeld of an-

other phase or phase assemblage, or of the new growth

of a metastable phase where it shouldn’t form, the

phase rule might be F  0. This negative variance re-

ﬂects an excess number of phases in the system and in-

dicates a state of disequilibrium.

5.2 MELTING OF A PURE MINERAL

AND POLYMORPHISM

5.2.1 Volatile-Free Equilibria

Additional useful concepts can be learned from the

one-component silica phase diagram (Figure 5.1). The

melting curve is equivalent to the freezing or crystal-

lization curve if T is decreasing; this curve lies between

the two ﬁelds where the liquid and crystals are in a state

of dynamic equilibrium. This means, that for any com-

bination of P and T along the curve, atoms are orga-

nizing from the liquid into crystals at the same rate that

other atoms from dissolving crystals are being added to

liquid. On this curve, there can be any proportion of the

two phases—a bit of liquid and lots of coesite, or vice

versa; provided they coexist in any proportion, equilib-

rium prevails. This suggests that the melting line is like

the buffer curves in Figures 3.13 and 3.14. Provided

phases coexist as indicated in the reaction represented

by the line, that is, crystals  melt in Figure 5.1, or

hematite  magnetite  O

in Figure 3.14, the equi-

librium is univariant. There is only one degree of free-

dom among the intensive variables; choose some T and

the other variable along the other axis of the diagram is

uniquely determined.

Qualitatively, we can predict how a state of equilib-

rium will shift if P or T changes by applying Le Chate-

lier’s principle and noting the inequalities in molar vol-

umes and entropies, as explained in Section 3.3.1.

States of smaller molar volume are more stable at

higher P and the more disordered states of higher en-

tropy are more stable at higher T. Slopes of equilibrium

boundary lines in P-T space can be determined from

the Clapeyron equation (3.13).

Silica polymorphs are widespread in the crust of the

Earth and provide insight into pressure of crystalliza-

tion. Tridymite and cristobalite are restricted to low-P,

high-T volcanic environments. Only rarely is the high-

P silica polymorph coesite found in crustal rocks, but it,

as well as stishovite, can occur in silica-rich meteorite-

impact rocks where transitory high P prevailed.

P in the mantle is adequate to stabilize coesite and

stishovite, but the low silica activity in most mantle sys-

tems precludes crystallization of any silica polymorph.

5.2.2 Melting of a Pure Mineral

in the Presence of Volatiles

Volatiles, especially water, are virtually always present

in magmatic systems and can have a profound impact

on their phase relations, including how they melt.

NaAISi

-H

O System. The system has served as a

model of granitic magmas since the 1930s. Without wa-

ter, dry albite melts along a positively sloping line in

P-T space (Figures 5.2 and 3.8). Melting shifts to higher

T at higher P as predicted from Le Chatelier’s principle

and the Clapeyron equation (3.13).

Addition of water to the system so it is water-

saturated drastically lowers the T of melting by as

much as 300°C at 2 kbar and 500°C at 10 kbar, com-

pared to that of the dry system (Figure 5.2). Addition

of water to the melt lowers the activity of the albite

Crystal-Melt Equilibria in Magmatic Systems

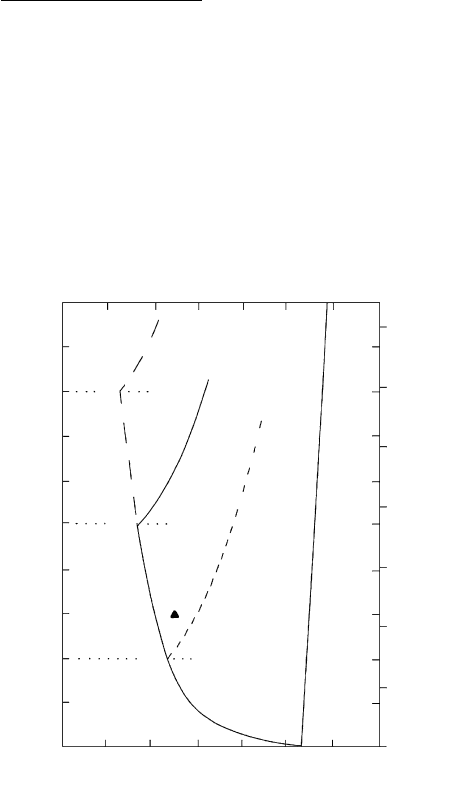
600 800 1000 1200

T (°C)

Depth (km)

MELT

WATER

2 kbar

Ab Water-free melting curve

Water-undersaturated

melting curve P

kbar

8 kbar

Water-saturated melting curve

P = P

ALBITE + WATER

P (kbar)

5.2 Melting of albite plagioclase with and without water. In a

dry, water-free system the virtually straight melting line (line

labeled Ab/L) has a steep positive slope. In contrast, the

melting curve in a hydrous NaAlSi

system in which

 5 kbar has a negative slope where water-saturated up

to 5 kbar and then turns to a positive slope in the water-

undersaturated region above 5 kbar where P

 P. For a

NaAlSi

-H

O system in which P

 8 kbar the nega-

tively sloping water-saturated melting curve (long-dashed line)

extends up to P  8 kbar at which pressure it turns positive.

The water-undersaturated part of the melting curve in a hy-

drous system in which P

 2 kbar is shown by the short-

dashed line. (Redrawn from Burnham and Davis, 1974;

Boettcher et al., 1982.)

component, but this reduction can be compensated by

reducing the T until ﬁnally the activity becomes unity

and albite crystallizes. A similiar depression of the

freezing T of water occurs when ethylene glycol, or an-

tifreeze, is added to it, a phenomenon familiar to any

owner of an automobile who wants to prevent water in

the radiator from freezing in cold climates. Another ex-

ample is the depression of the freezing T of seawater,

relative to pure water, because of the dissolved salt. But

dilution cannot be the complete explanation, as can be

appreciated from the following data. At 2 kbar, a water-

saturated NaAlSi

melt contains about 6.4 wt.%

O, which is equivalent to about 20 mole % H

O be-

cause of the large difference in the weight per mole

of water and albite. In contrast, addition of 6.4 wt.%

SiO

to NaAlSi

lowers the melting T only 20°C at

2 kbar (Burnham, 1979). Therefore, the more substan-

tial freezing point depression due to addition of water

is related to the way it dissolves in a melt, breaking

Si-O polymers.

The depression of the water-saturated melting curve

at increasing P is a general phenomenon in silicate min-

eral systems.

Figure 5.2 shows the effects of decompression on an

ascending water-saturated melt. For example, a water-

saturated melt (ﬁlled triangle) at 3 kbar and 850°C will

track along an adiabatic decompression curve, experi-

encing only a slight drop in T. The system will become

crystalline at P  2 kbar.

Suppose there is only sufﬁcient water to saturate the

melt at, say, 5 kbar. In this system, the water pressure,

 5 kbar, and so for P  5 kbar the system is

water-undersaturated and the melting curve will track

off on a positive slope in Figure 5.2.

The depression of the melting T resulting from dis-

solved CO

is substantially less than that of water at the

same P because of its lower solubility in the melt. A

mixture of H

O and CO

, however, depresses the

ﬂuid-saturated melt curve signiﬁcantly. Dissolved ﬂuo-

rine depresses the melting T more than CO

because of

its greater solubility in the melt.

5.3 PHASE RELATIONS IN

BINARY SYSTEMS

In a one-component phase diagram, two relevant in-

tensive variables—P and T—can be conveniently rep-

resented on a two-dimensional sheet of paper. The

compositions of all phases are ﬁxed; there is no varia-

tion in their composition. In two-component, or binary

(and more complex), systems a choice must be made as

to which of the intensive variables to hold constant in

representing equilibria in two dimensions. Virtually all

phases in rock-forming systems have variable composi-

tion so most binary diagrams portray the proportions

of two components, either on a weight or a mole basis,

along the horizontal axis. The vertical axis can be P,

with T ﬁxed in an isothermal P-X diagram, or it can be

T, with P ﬁxed in an isobaric T-X diagram. For a com-

plete understanding of the system, more than one of

these diagrams has to be examined or special projec-

tion devices employed.

5.3.1 Basic Concepts: CaMgSi

(Di)-CaAl

(An) System at P  1 atm

The binary CaMgSi

-CaAl

system was one of

the ﬁrst elucidated, in 1915, by N. L. Bowen. It serves

a twofold purpose: ﬁrst, as an introduction to reading

binary phase diagrams; second, as a demonstration of

some basic concepts of crystal-melt equilibrium in a

simple model “basalt” magma in which plagioclase

and pyroxene crystallize. For brevity, the CaMgSi

component is sometimes designated as Di and the

CaAl

component as An. In this binary system,

the chemical formulae of the two components are the

same as the chemical formulae of crystalline phases.

However, in many systems, formulae of phases are dif-

ferent from formulae of the components.

Crystallization and Liquidus Relations. This binary iso-

baric T-X diagram can be introduced by means of the

concept of freezing (melting) point depression as an-

other component is added. In Figure 5.3, T

is the

90 Igneous and Metamorphic Petrology

Special Interest Box 5.1 N.L. Bowen, pioneer

experimental petrologist

It has been said that “just as modern biology

would be unthinkable without the overarching ge-

nius of Darwin, modern igneous petrology would

be unthinkable without the overarching genius of

Norman Levi Bowen” (Young, 1998, p. 253). Bowen

not only attacked many of the core problems in

petrology but did so decades ahead of anyone else

and with such insight that subsequent investigations

have only built upon his pioneering work. Added to

his experimental acumen was a gift for ﬂuency in

writing that enabled him to broadcast the results of

a new discipline in a way that almost any geologist

could understand. His 1928 book, The evolution of

the igneous rocks, served as the fundamental text-

book for half a century and is still widely used.

His determinations of fundamental phase equilibria

in the plagioclase, pseudobasalt, and granite sys-

tems are described in this chapter. Other contribu-

tions and the debates they generated are referred to

in subsequent chapters. The biography by Young

(1998) is especially interesting, not only about

Bowen, but about igneous petrology in general for

Bowen occupied a central position in this discipline

for much of the ﬁrst half of the 20th century.

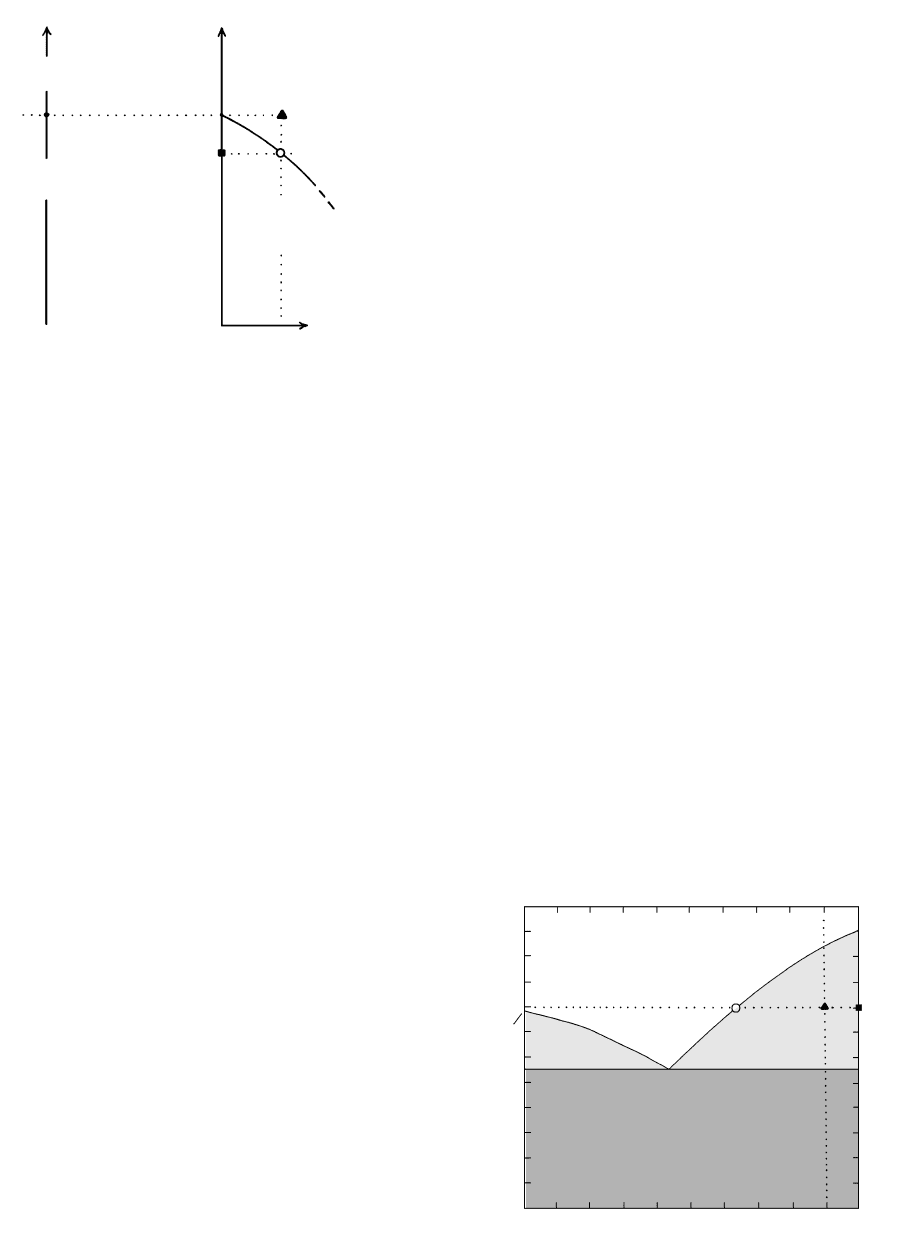
freezing or crystallization T of a pure CaMgSi

melt

(or melting T of pure crystals of diopside) in a one-

component system. Suppose at T

, where melt (liquid)

and diopside crystals coexist in equilibrium, another

component, which does not form a solid solution with

diopside, such as CaAl

, is added to and dis-

solved in the melt. This dilutes the melt in the origi-

nal single component, CaMgSi

, and depresses the

freezing T of the now-two-component liquid to, for

example, T

. With the T of the system still at T

the

diopside crystals have dissolved into the melt and the

system consists only of the two-component melt (rep-

resented by the ﬁlled triangle in Figure 5.3). At T

the

melt (represented by an open circle), which is in equi-

librium with crystals of pure diopside (ﬁlled square),

contains all of the added component, CaAl

, plus

some additional CaMgSi

. Adding still more of the

second component depresses the freezing T still lower

as the composition of the melt shifts farther to the right

along the downward inclined dashed line. This line

representing the locus of depressed freezing (melting)

T points as more of the second component is added to

the melt is called the liquidus.

Figure 5.3 is a part of the left-hand side of Figure

5.4, which is the complete T-X phase diagram of the

CaMgSi

-CaAl

system at a ﬁxed P  1 atm.

On the vertical T axis on the left side of Figure 5.4 is

the freezing T of a pure CaMgSi

melt at 1392°C

and on the right T axis is the freezing T of pure

CaAl

melt at 1553°C. Between these two pure

end members, melts of mixtures of the two compo-

nents freeze at declining temperatures, as indicated by

the two oppositely sloping liquidus line segments that

merge at point E, called the eutectic point. Mixtures of

the two components are completely liquid (a crystal-

free melt) at temperatures above the liquidus; this is a

second meaning of this term.

To understand more of the vast amount of informa-

tion in this binary diagram, especially in the two-phase

ﬁelds of liquid  diopside and liquid  anorthite, it is

necessary to get acquainted with some special lines and

another rule. An isopleth is a line of constant composi-

tion in terms of the components in the diagram. In Fig-

ure 5.4, it is a vertical line drawn, for example, at An

that represents 90 wt.% of CaAl

and 10 wt.% of

CaMgSi

. An isothermal line, or isotherm, is a line

of constant T; it is a horizontal line drawn, for example,

at 1400°C. The intersection of these two lines is a point

(ﬁlled triangle) representing the T (1400°C) and bulk

chemical composition (An

) of a system that consists

of two phases—liquid (melt) and pure anorthite crys-

tals. But what is the composition of the liquid, and

what is the modal proportion of liquid and crystals? To

answer these questions, note that the isotherm inter-

sects the liquidus line at a point, designated L and

shown by an open circle, and also intersects an isopleth

through pure An at a point, designated S (for solid) and

shown by a ﬁlled square. The line segment of the

isotherm connecting points L and S is called a tie line;

it connects two stably coexisting phases at points rep-

resenting their compositions in terms of the system

components. Point S obviously is equivalent to the

composition of anorthite crystals, CaAl

. Point L

represents the composition of the coexisting melt at

1400°C, found by drawing a vertical isopleth through

point L to the base of the diagram and reading An

Thus, the liquidus is the locus of points representing

the composition of liquid coexisting with a solid phase

(or phases) at a particular T; this is a third meaning of

the term. The compositions of crystals and liquid just

determined are analogous to the mineralogical compo-

sition of a rock.

Crystal-Melt Equilibria in Magmatic Systems

CaMgSi

CRYSTALS

LIQUID

CRYSTALS

+ LIQUID

Additional

component

CaMgSi

Liquidus

5.3 Depression of the melting T of diopside due to addition of an-

other component to the system.

1000

1274

1392

1400

1600

1200

20 40 60 80 100

T (°C)

1553°

CaMgSi

wt. % CaAl

P = l atm

Isotherm

LIQUID

L +

Diopside

L + Anorthite

Diopside + Anorthite

crystals

Isopleth

5.4 Binary system CaMgSi

(Di)-CaAl

(An) at 1 atm. Dia-

gram is simpliﬁed from Yoder (1976), who discusses com-

plications due to the fact that the pyroxene is not pure

CaMgSi

but contains Al in solid solution.

What about the modal composition, or the propor-

tion of the two phases, in the system posed as the sec-

ond question? This is solved by using the lever rule,

which can be formulated as follows: The isothermal tie

line passing through the bulk composition point (ﬁlled

triangle) has end points S and L, representing coexist-

ing solid and liquid phases at 1400°C, respectively.

Imagine this tie line to be a mechanical lever carrying

masses S and L and resting on a fulcrum, the ﬁlled tri-

angle, in Figure 5.5. For equilibrium (as on a balanced

“teeter-totter” in a children’s playground), the weight

fraction of the solids, S, multiplied by their lever arm,

y, must equal the weight fraction of liquid, L, multi-

plied by its lever arm, x, or Sy  Lx. But as S  L  1,

Sy  (1  S)x  x  Sx or

5.2 S 



(y 



which is the lever rule. Thus, we measure in Figure 5.4

the distances x and y, say, in millimeters, and calculate

the ratio, in this case 0.72, which is the weight fraction

or proportion of solids, anorthite crystals, in the system

at 1400°C whose bulk chemical composition is An

This fraction multiplied by 100 is the weight percent-

age (wt.%) crystals, 72%; the remaining 28 wt.% is

melt. To prevent possible confusion, note that in this

example the bulk composition point lies closer to the

solids (crystals) point, S, than it does to the liquid

point, L; accordingly, there is a greater proportion of

crystals than liquid.

An instructive exercise is to track the crystallization

of a melt, say An

, from above the liquidus. As the

melt cools, the ﬁrst crystals, of pure anorthite, appear

at 1520°C. As T decreases, and equilibrium prevails,

more anorthite precipitates, accordingly driving the co-

existing remaining residual liquid down the liquidus

toward more Di-rich compositions. These increasingly

more Di-rich residual liquid compositions together

with changing modal proportions of liquid and anor-

thite crystals can be tracked by drawing a series of

isothermal tie lines, dropping isopleths to the composi-

tion axis from the liquid composition end point of the

tie line that lies on the liquidus, and applying the lever

rule to determine the modes. At 1274°C, as more heat

is withdrawn form the system, its T remains ﬁxed at

this eutectic temperature T

, until all of the liquid of

eutectic composition, E, has crystallized to pure anor-

thite and diopside in 90/10 weight ratio.

Figure 5.6 shows thermal relations in the cooling

system above and below T

. The T in the system drops

continuously as heat is lost where T  T

. But, at T



1274°C, no change in T occurs during further loss of

heat from the system because of the compensating con-

tribution of the latent heat, or enthalpy, of crystalliza-

tion of diopside (H

, Figure 3.3) and of anorthite,

H

. Only after all of the melt has been crystallized

into the diopside and anorthite and their latent heats

dissipated can T once again fall.

The eutectic point, E, is the only invariant point in

the isobaric binary diagram. For ﬁxed P, from the

phase rule, F  1  C    1  2  3  0. This

means that every intensive variable in the system is

ﬁxed at this point: P (given as 1 atm), T (1274°C), and

the composition of all three coexisting phases, melt

 An

(Di

) and pure crystals of anorthite and

diopside. This unique eutectic point lies at the juncture

of four stability ﬁelds:

1. Liquid

2. Diopside  anorthite, below an isothermal hori-

zontal line at 1274°C

3. Liquid  diopside, a crudely triangular ﬁeld on the

Di-rich side of the diagram

4. Liquid  anorthite, another crudely triangular ﬁeld

on the An-rich side of the diagram

92 Igneous and Metamorphic Petrology

5.5 Lever rule. See text for explanation.

+ ∆H

∆H

+ ∆H

+ C

1274

1520

T (°C)

Time

5.6 Hypothetical cooling history (T-time relations) for a model

magma An

in the binary system CaMgSi

-CaAl

los-

ing heat to its surroundings. Compare Figure 3.3. The time

rate of cooling (loss of thermal energy) of the magma is as-

sumed to be constant, that is, heat loss is proportional to time.

The crystal-free melt falls relatively rapidly in temperature

above the liquidus (T  1520°C) because only its speciﬁc heat,

, must be dissipated. During its excursion through the two-

phase region (T  1520  1274°C), the crystallizing magma

cools more slowly because the latent heat of crystallization (the

enthalpy of melting, H

) must also ﬂow out of the system.

At the eutectic T, 1274°C, the invariant system remains ﬁxed

in T for a period as the latent heat of crystallization of both

anorthite and diopside is dissipated into the surroundings. In

well-insulated, intrusive natural magma systems, the latent

heat is dissipated very slowly and therefore crystallization

takes a long time.

In the isobaric one-phase ﬁeld consisting only of

melt above the liquidus, divariant equilibria prevails,

F  1  C 1  2  1  2. Two degrees of free-

dom means that T and X must both be speciﬁed in or-

der to know all about the system: that is, to ﬁx a point

in the ﬁeld by an intersecting isopleth and isotherm.

In the isobaric two-phase ﬁelds of the binary system,

univariant equilibrium prevails, F  1  2  2  1.

For example, if anorthite  liquid are stable in a sys-

tem, speciﬁcation of one variable, say T, uniquely ﬁxes

the composition of the liquid, the only other intensive

variable. Modal proportions of phases do not constrain

intensive variables in equilibria, but chemical composi-

tions of coexisting phases do. This important principle is

the basis of mineral geothermometers and geobarome-

ters discussed in Sections 3.5.5, 5.8 and 16.11.3.

The fourth and ﬁnal signiﬁcance of the liquidus is

that it is a saturation line. At a T of, say, 1350°C in Fig-

ure 5.4, melts whose compositions lie between An

and An

are unsaturated in any crystalline phase: No

crystals coexist with these melts because their concen-

trations have not exceeded their solubility (activities

1). However, melts more enriched in CaAl

than An

are oversaturated in this component, and

accordingly crystals of anorthite coexist at equilibrium

with these melts.

The CaMgSi

-CaAl

system serves as a

very simpliﬁed model of how basaltic magmas crystal-

lize. Magmas with relatively large concentrations of

CaAl

precipitate a calcic plagioclase as the liq-

uidus phase, the ﬁrst crystalline phase to appear at the

liquidus with decreasing T from a wholly liquid state.

After a calcic plagioclase has grown over a range of T,

a diopside-rich pyroxene then co-precipitates at the eu-

tectic. Such basaltic magmas would be expected to

contain high-T phenocrysts of plagioclase in a ﬁner ma-

trix that includes pyroxene. Basaltic magmas that con-

tain more CaMgSi

have pyroxene phenocrysts and

plagioclase only occurs in the matrix.

Melting and Solidus Relations

Melting accompanying

increasing T is the reverse of crystallization, provided

equilibrium is maintained.

A perhaps unexpected result of heating an aggregate

of diopside and anorthite crystals, in any modal propor-

tion, is that melting occurs at the same T  1274°C, the

eutectic temperature, and yields the same unique com-

position melt, An

(Di

), the eutectic composition.

This unique melting at the eutectic point for any anor-

thite-diopside “rock” can be visualized by drawing a

series of horizontal isotherms at increasing T in the

anorthite  diopside stability ﬁeld. No melting occurs

until the T  T

 1274°C. In this binary system, this

1274°C isotherm is a solidus, at all temperatures below

which any mixture of the components consists only of

crystalline solids, provided equilibrium prevails.

Although any proportion of diopside and anorthite

crystals begins to melt at 1274°C, and the composition

of the ﬁrst “drop” of melt is An

; continued melting at

higher T follows one of two paths. Model “rocks” that

contain more than 42 wt.% anorthite crystals cannot

rise in T above 1274°C until all of the diopside in the

rock has melted. Input heat is absorbed in the latent

heat of melting of diopside, H

, at constant T (com-

pare Figure 5.6). Slightly above 1274°C only crystals of

anorthite remain unmelted, and these are in equilib-

rium with a liquid that is just slightly more enriched in

CaAl

than the eutectic composition. After the

diopside is completely melted, more heat added to the

system simply results in an increase in T proportional

to the heat capacity of the system of melt plus anor-

thite. As T increases, and if equilibrium prevails, an in-

creasing amount of anorthite dissolves in the melt, in-

creasing the concentration of CaAl

in the liquid.

These changing liquid compositions and modal pro-

portions of melt and anorthite crystals can be tracked

by drawing a series of isothermal tie lines, dropping

isopleths to the composition axis from the liquid com-

position end point of the tie line that lies on the liq-

uidus, and applying the lever rule to determine the

modes. Finally, at 1520°C, the An

bulk-composition

isopleth intersects the liquidus, the proportion of solids

in the system by the lever rule is now zero, or melting

is complete. The system is entirely liquid at T 

1520°C.

5.3.2 Mg

SiO

-SiO

System at 1 atm

The phase diagram (Figure 5.8) of this simple, yet sig-

niﬁcant system, elucidated by Bowen and Anderson

(1914), has a eutectic point, E, similar to that in the

CaMgSi

-CaAl

system. Melts lying between

about 61 and 70 wt.% silica crystallize in similar man-

ner to melts in that system. The Mg

SiO

-SiO

sys-

tem provides valuable insight about magma genera-

tion and evolution and is especially important in

demonstrating phase incompatibility, reaction rela-

tion, contrasts between equilibrium and fractional

crystallization, incongruent melting, and liquid immis-

cibility.

Phase Incompatibility. Countless observations of mag-

matic rocks indicate that certain minerals never oc-

cur together, except in rare accidental circumstances.

There can be two reasons for this. Because of the way

natural magmas originate and evolve, minerals that

typically precipitate at highest temperatures from the

least-evolved systems are seldom, if ever, found to co-

exist with minerals that precipitate at lowest tempera-

tures from highly evolved magmas. For this reason,

high-T forsterite and low-T albite are unlikely associ-

ates, even though they can coexist stably. In contrast,

nepheline-quartz and forsterite-quartz are pairs of

Crystal-Melt Equilibria in Magmatic Systems

94 Igneous and Metamorphic Petrology

with G

crystals

, that is, at the melting T of pure diopside

crystals. At T

the tangent relation described holds

for both components. As T decreases below T

the

two tangent points converge and ﬁnally at T  T

there is only one tangent because 

is the same in

all three phases and a different value of 

is the

same in all three phases.

Advanced Topic Box 5.2 G-T-X sections for

the binary system CaMgSi

(Di)-CaAl

(An) at 1 atm

It may be recalled from Section 3.3 that a phase

diagram portraying stable equilibria in terms of T

and X or any other combination of intensive vari-

ables implies a minimum of the Gibbs free energy, G,

or chemical potential for the stable phases. Thus, the

P-T diagram in Figure 3.6 indicates which phases are

stable as a function of P and T from the G-P-T dia-

gram in Figure 3.7. Similarly, the binary T-X diagram

for the CaMgSi

-CaAl

system in Figure 5.4

indicates which phases are stable as a function of

T and X from the sequence of G-X diagrams at dif-

ferent temperatures in Figure 5.7. This ﬁgure is

presented here to emphasize that stable phases and

phase assemblages have minimal free energies or

chemical potentials, even though they are not explic-

itly shown in a phase diagram plotted in terms of in-

tensive variables. The presentation here follows An-

derson (1996).

In Figure 5.7, the G of a physical mixture of di-

opside and anorthite crystals with no mutual solid

solubility is simply a straight line between G

and

. On the other hand, G for any solution, whether

liquid silicate (melt) or solid crystals, is a convex-

downward curve, or loop (Figure 3.11). Because

dG/dT  S, the G straight line representing the

mix of crystals and the G loop representing liquid

both move upward to greater G with decreasing T,

but the G loop moves more, for a given increment

in T, because the entropy of a liquid is greater. At

above the liquidus, liquid of any composition be-

tween the two end-member components CaMgSi

(Di) and CaAl

(An) has a lesser G than a

mixture of diopside and anorthite crystals; hence,

the liquid is more stable and the crystal mix is

metastable. At T

below the solidus, the opposite is

true. At T

, G for both liquid and crystals has in-

creased, but more for the liquid, so that the G of

liquid CaAl

has become greater than that of

anorthite crystals, but the G of liquid CaMgSi

remains less than that of diopside crystals. From

Figure 3.11, the tangent to the free energy curve for a

solution intercepts the An vertical axes at the chemi-

cal potential of the An component in the solution,



liquid



crystals

. This equality means that the melt

on the liquidus at T  T

in the T-X phase diagram

is in equilibrium with crystals of pure anorthite. As

T decreases below T

, that tangent point slides along

the loop toward greater Di concentrations because

the loop is rising relative to the G

crystals

, and at some

T  T

but  T

the left end of the loop coincides

CaMgSi

CaAl

Solid mix

Liquid

Solid mix

and anorthite crystals

Mixture of diopside

G-X section at T

T-X section at

fixed P

5.7 Sequence of G-X sections for the binary system CaMgSi

(Di)-CaAl

(An) at 1 atm. Top ﬁve frames are G-X sec-

tions for ﬁve temperatures. Lowest frame is the T-X section

(Figure 5.4). (From Anderson, 1996.)

minerals that are thermodynamically unstable. Rare

magmatic rocks might contain both magnesian olivine

and quartz, but one or both will likely be corroded, or

partially resorbed, indicating a state of disequilibrium

that was frozen into the rock. The Mg

SiO

-SiO

sys-

tem conﬁrms that forsterite and quartz cannot coexist

in equilibrium at 1 atm (or at any P, for that matter) but

react to form more stable, intermediate composition

enstatite.

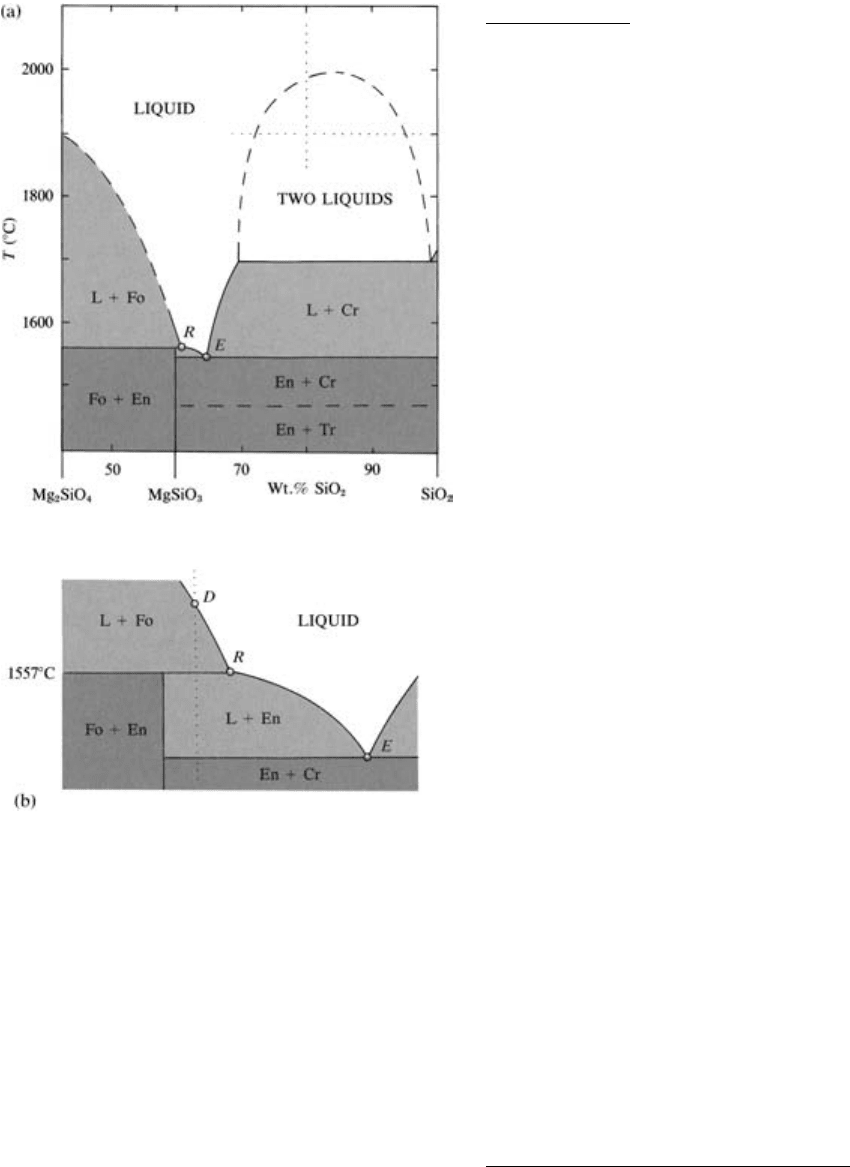
Reaction Relation. Consider the crystallization behav-

ior of a melt cooling from 1900°C and containing

50 wt.% silica, a concentration found in basalts. The

50 wt.% isopleth intersects the liquidus at about

1815°C, at which T forsterite crystals begin to precipi-

tate. After further cooling to 1558°C, the system con-

sists, at equlibrium, of about 60 wt.% forsterite crystals

and 40 wt.% melt, from the lever rule. At 1556°C, the

system is below the solidus and consists of about

58 wt.% forsterite crystals and 42 wt.% enstatite crys-

tals. At 1557°C, there are stably coexisting forsterite,

enstatite, and a liquid, R, slightly more silica-rich

(about 61 wt.%) than enstatite crystals (59.85 wt.%).

To explain the disappearance of 2 wt.% forsterite be-

tween 1558°C and 1556°C, these crystals must be re-

sorbed, or dissolved into the melt, R, at 1557°C ac-

cording to the reaction

5.3 Mg

SiO

 SiO

 2MgSiO

 latent heat

forsterite in melt enstatite

This is an example of a reaction relation in which crys-

tals of one composition react with melt of another com-

position yielding crystals of a third composition.

At 1557°C, the isobaric equilibrium in this binary

system of the three phases—forsterite, enstatite, and

liquid R—is invariant. Point R on the liquidus is called

a peritectic.

Crystallization of a melt which contains 59.85 wt.%

silica and 40.15 wt.% MgO—the composition of

enstatite—further illustrates what happens in crystal-

melt equilibria at the peritectic reaction point, R. As this

unique melt cools, forsterite begins to crystallize at

about 1600°C and continues to precipitate until at

1557°C it is resorbed into the melt R, yielding at 1558°C

only enstatite as the sole ﬁnal phase in the cooling sys-

tem. The system is “stuck” isothermally at 1557°C

until all of the forsterite and melt are consumed in the

reaction to produce enstatite before the T of the system

can decrease as heat is continually withdrawn from

it. Note the thermal similarity with eutectic behavior

(Figure 5.6).

Reaction relations of the sort just described are uni-

versal in natural magmas and are a factor contributing

to the great compositional diversity of magmatic rocks

(Figure 2.4). The following paragraphs begin to ex-

plain how and why this is so.

Equilibrium versus Fractional Crystallization. Magmas

crystallize in some manner between two ideal end

members:

1. Perfect equilibrium crystallization, in which crys-

tals continually react and reequilibrate completely

with melt as P-T-X conditions change. Crystal-melt

reaction relations are reversible at any point in the

process.

Crystal-Melt Equilibria in Magmatic Systems

5.8 Binary system Mg

SiO

-SiO

at 1 atm. Stability ﬁelds that con-

tain melt (silicate liquid) plus a crystalline phase are lightly

shaded; stability ﬁelds that contain two crystalline phases are

shaded dark. Proportions of the silica component along the

bottom of the diagram are with respect to the binary system

MgO-SiO

, of which this is a part. Fo, forsterite; En, enstatite;

Cr, cristobalite; Tr, tridymite; L, liquid. Pure forsterite con-

tains 42.7 wt.% SiO

enstatite 59.85, point R about 61, and

point E about 65. Lower part of the ﬁgure is an enlarged and

slightly distorted region of the phase diagram in the vicinity of

the peritectic reaction point, R. (Redrawn from Bowen and

Anderson, 1914.)

2. Perfect fractional crystallization, in which crystals

are immediately isolated, removed, or fractionated

from the melt as soon as they form so that no crys-

tal-melt reaction relation occurs as P-T-X condi-

tions change. Reactions are irreversible.

Perfect equilibrium crystallization obviously has

stringent requirements. At any particular set of values

of intensive variables, each phase must be homoge-

neous and uniform in composition; the melt must

everywhere be exactly the same composition. Rates of

changes in intensive variables must be slower than the

slowest kinetic process so the magma can keep up with

the changes. Changes in intensive variables can be re-

versed at any time and a former state of equilibrium in-

volving unique melt and crystal compositions can be

restored or recovered. There can be no physical sepa-

ration of phases. The total composition of the system

cannot change; the initial composition of the system

must be maintained, so it is strictly a closed system.

Every part communicates with every other part. This

ideal reversible process of equilibrium crystallization

may only be approached, rarely, in deep plutonic

systems that cool very slowly. The examples given pre-

viously of crystallization along the 50 and 59.85 wt.%

silica isopleths described equilibrium crystallization.

Fractional crystallization is quite different. It is real-

ized to varying degrees in virtually all magmas because

reaction relations between crystals and melt are incom-

plete as a result of sluggish kinetics. In the extreme,

ideal case, no reactions whatsoever occur between liq-

uid and crystals, once they have precipitated, during

changing states of the system. To prevent reaction there

must be a separation, isolation, or fractionation of melt

from crystals. This fractionation can occur in one of

three ways, or by combinations thereof:

1. It can occur by physically separating whole crystals

and liquid as a result of differences in their densit-

ies or other dynamic processes in magmas.

2. Crystals and melt simply do not react because the

kinetics are too slow. In the ever-present contest be-

tween changing intensive variables in magma sys-

tems and kinetically controlled equilibration be-

tween phases, the latter loses.

3. Fractionation can occur by growing an armoring or

protective layer of another composition on the ini-

tial crystal, thereby effectively separating it from

the liquid and precluding any reaction between

them. This is a common and widespread means of

fractionating crystals from coexisting melt in nat-

ural magmas. In a fractionating basaltic magma,

modeled by the Mg

SiO

-SiO

system, stable en-

statite might form at the interface between melt and

forsterite, creating a reaction rim on the metastable

forsterite at the peritectic. This overgrowth can de-

velop during relatively rapid changes in intensive

variables so the magma system “tries to catch up”

by precipitating the new stable phase before the

metastable crystals have been eliminated by reac-

tion with the melt.

Fractional crystallization can be illustrated by a

thought experiment using the Mg

SiO

-SiO

system.

Consider again a melt that contains 50 wt.% silica (Fig-

ure 5.8). At 1815°C, forsterite crystals begin to precip-

itate, but are immediately isolated or fractionated—by

either 1. or 2.—from the liquid. In effect, the bulk

composition of the system is all melt more silica-rich

than 50 wt.% as the system has no “memory” of its ini-

tial composition. Further cooling results in further pre-

cipitation of forsterite, which is immediately isolated

from the enclosing melt. Eventually, as fractionation

continues, the residual melt—which may be consid-

ered to be the whole system that has “forgotten” about

its previously precipitated crystals—reaches the peri-

tectic, R, at 1557°C. Here, fractionation might be ac-

complished by forming reaction rims of stable enstatite

around previously precipitated forsterite crystals as T

decreases. Continued cooling results in further precip-

itation of enstatite, which is fractionated from the sys-

tem. Ultimately, the residual melt reaches the eutectic,

E, at 1543°C, where enstatite and cristobalite (the sil-

ica polymorph that is stable at this T) coprecipitate.

Crystallization is complete.

Important contrasts between equilibrium and frac-

tional crystallization are immediately apparent, as fol-

lows:

1. For this particular composition (50 wt.% silica),

the residual fractionated melt was not all consumed

at the peritectic as it was in equilibrium crystalliza-

tion.

2. The range of temperatures over which fractionation

occurred is greater than that of equilibrium crystal-

lization.

3. The compositional path of evolving residual melts

portrayed on a variation diagram, the liquid line of

descent, has a more extended range in a fractionat-

ing system than does the path deﬁned by successive

melts during equilibrium crystallization (Figure

5.9). However, by either mode of crystallization,

residual melts after some crystallization has oc-

curred in the Mg

SiO

-SiO

system are enriched in

SiO

and depleted in MgO relative to the initial

melts. This same liquid line of descent—depletion

in MgO and enrichment in SiO

—typiﬁes many

natural crystallizing multicomponent magmas.

4. The crystalline products of fractional crystallization

are also more extended in their range of composi-

tions than those that develop by equilibrium

crystallization (Figure 5.9). The ﬁnal crystalline

product created by closed system equilibrium crys-

tallization—forsterite plus enstatite—occurs in a

96 Igneous and Metamorphic Petrology