Никишкин В.А., Малахов А.Н., Максюков Н.И. Высшая математика
Подождите немного. Документ загружается.


Пусть частная производная ),...,(
1 m
i
xx
x
u
∂
∂
функции u=f(x
1
,...,x
m
) существует в
каждой точке некоторого множества {M}, т.е. представляет собой функцию
переменных x
1
, ..., x
m
.
Если эта функция имеет частную производную по переменной х
k
в
некоторой точке М
0
, то она называется второй частной производной функции f(x
1
,
..., x
m
) по переменным x
i
и x
k
и обозначается
. ,
2
ki
xx
ik
f
xx
u
′′
∂∂
∂
Совершенно аналогично определяются и последующие частные
производные функции f.
Таким образом,
=
−−
−
121121
......
1
iii
n
iiiii
n
xxx
u
xxxxx
u
nnnn
∂∂∂
∂
∂
∂
∂∂∂∂
∂
Если не все индексы i
1
, ..., i
n
совпадают между собой, то частная
производная называется смешанной.
Вычисляются частные производные по тем же правилам, что и
обыкновенные производные. Необходимо только следить при каждом
дифференцировании, чтобы все переменные, кроме одной, считались
постоянными.
Пример 1.
y
x
e=u Вычислить все частные производные второго порядка.
−
⋅⋅=
2
;
1
y
x
e
y
u
y
e
x
u
y
x
y
x
∂
∂
∂
∂
232
2
1
y
e
y
x
e
y
x
e
xy
u
xyx
u
y
x
y
x
y
x
⋅−
−
⋅=
−
⋅=
=
∂
∂
∂
∂
∂
∂
∂∂
∂
(Здесь y = const)
−
⋅+
−
⋅=
⋅=
=
23
2
11
y
e
y
x
e
y
e
yx
u
yxy
u
y
x
y
x
y
x
∂
∂
∂
∂
∂
∂
∂∂
∂
(Здесь х = const)
22
22
11
y
e
y
e
xx
u
xx
u
xx
u
y
x
y
x
⋅=
⋅=
=≡
∂
∂
∂
∂
∂
∂
∂
∂
∂∂
∂
(Здесь y = const)
34
2
22
22
2
y
x
e
y
x
e
y
x
e
yy
u
yy
u
yy
u
y
x
y
x
y
x
⋅+⋅=
−
⋅=
=≡
∂
∂
∂
∂
∂
∂
∂
∂
∂∂
∂
(Здесь х = const)
Замечание. В этом примере
xy
u
yx
u
∂∂
∂
∂∂
∂
22
= . Равенство смешанных производных
будет иметь место не всегда, а при выполнении некоторых условий; а именно,
справедлива следующая теорема.
Теорема. Пусть функция u=f(x
1
, ..., x
m
) определена в открытой m - мерной
области D и имеет в этой области всевозможные частные производные n-го

порядка, причем все эти производные непрерывны в D. Тогда значение любой к-
ой смешанной производной не зависит от того порядка, в котором производятся
последовательные дифференцирования.
В подавляющем большинстве конкретных задач условия теоремы выполняются, и
смешанную производную можно вычислять, не обращая внимания на порядок
последовательных дифференцирований.
9.7.2. Дифференциалы высших порядков
Пусть в некоторой области задана дифференцируемая функция
u=f(x
1
, ..., x
m
), тогда в каждой точке этой области определен дифференциал
m
m
dx
x
u
dx
x
u
du
∂
∂
∂
∂
++= ...
1
1
Здесь частные производные являются функциями от x
1
, ..., x
m
. Если
существуют непрерывные частные производные второго порядка для u, то du
будет иметь непрерывные частные производные по x
1
, ..., x
m
. Будем считать, что
dx
1
, ..., dx
m
постоянны, тогда можно определить дифференциал от первого
дифференциала:
m
m
m
m
dx
x
u
ddx
x
u
ddx
x
u
dx
x
u
ddud
++
=
++=
∂
∂
∂
∂
∂
∂
∂
∂
......)(
1
1
1
1
При вычислении дифференциалов от частных производных будем считать,
что dx
1
, ..., dx
m
имеют те же самые значения, что и в исходном дифференциале du.
mm
mmm
m
m
dxdx
x
u
dx
xx
u
dx
xx
u
dxdx
xx
u
dx
xx
u
dx
x
u
dud
++++
+
+++=
2
2
2
2
2
1
1
2
1
1
2
2
21
2
1
2
1
2
...
......)(
∂
∂
∂∂
∂
∂∂
∂
∂∂
∂
∂∂
∂
∂
∂
Полученное таким образом выражение мы назовем дифференциалом
второго порядка функции u
mm
mm
m
m
m
m
dxdx
xx
u
dxdx
xx
u
dxdx
xx
u
dxdx
xx
u
dx
x
u
dx
x
u
ud
1
1
2
32
32
2
1
1
2
21
21
2
2
2
2
2
1
2
1
2
2
2...22
...2)(...)(
−
−
++++
++++=
∂∂
∂
∂∂
∂
∂∂
∂
∂∂
∂
∂
∂
∂
∂
Точно так же мы определим и последующие дифференциалы функции u с
помощью равенства
)(
1
uddud
kk −
=
Пример 1. z = x
2
y
3
Найти d
2
z
.)(662)(2)(2)(
6 ;6 ;2 ;3 ;2
22232
2
22
2
2
2
2
2
2
2
2
2
3
2
2
223
dyyxVxydxdydxydy
y
z
dxdy
yx
z
dx
x
z
zd
yx
y
z
xy
yx
z
y
x
z
yx
y
z
xy
x
z
++⋅+=++=
===⋅==
∂
∂
∂∂
∂
∂
∂
∂
∂
∂∂
∂
∂
∂
∂
∂
∂
∂
Развернутые выражения для дифференциалов высших порядков довольно
громоздкие. Однако, символически они записываются очень компактно. Запишем
дифференциал в символической форме.
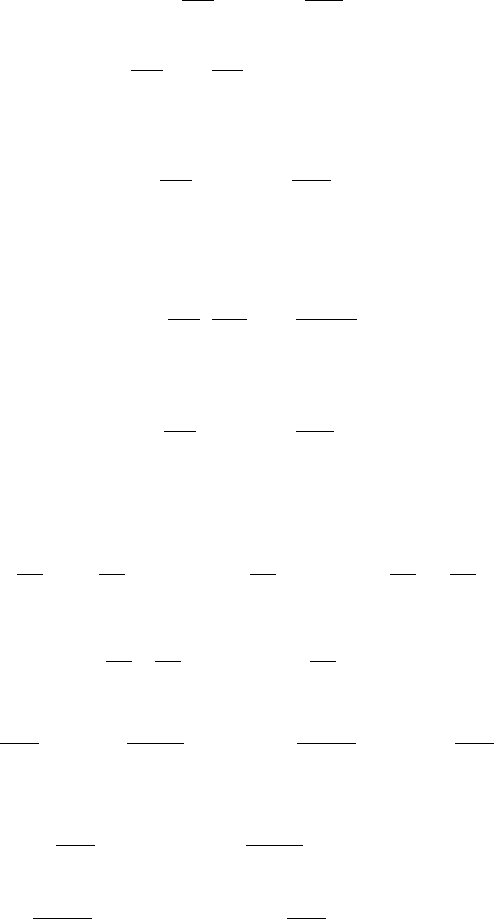
udx
x
dx
x
du
m
m
++=
∂
∂
∂
∂
...
1
1
(u вносим в скобки и считаем
ii
x
u
u
x
∂
∂
∂
∂
≡⋅ и получаем обычное выражение для du).
Тогда
uxd
x
dx
x
ud
m
m
⋅
⋅++⋅=
2
1
1
2
...
∂
∂
∂
∂
.
Здесь выражение в скобках возводится по обычным правилам в квадрат и
затем считаем, что
jiji
xx
u
u
xx
∂∂
∂
∂
∂
∂
∂
2
≡⋅⋅
Выражение для дифференциала порядка
к принимает вид:
udx
x
dx
x
ud
k
m
m
k
⋅
⋅++⋅=
∂
∂
∂
∂
...
1
1
.
Пример 2. z = x
2
y
3
Вычислить d
3
z
3
3
3
2
2
3
2
2
3
3
3
3
3
3
2
2
2
2
3
3
3
3
)()(3)(3)(
)()(3
)(3)(
dy
y
z
dydx
yx
z
dydx
yx
z
dx
x
z
zdy
y
dydx
yx
dydx
yx
dx
x
zdy
y
dx
x
zd
∂
∂
∂∂
∂
∂∂
∂
∂
∂
∂
∂
∂
∂
∂
∂
∂
∂
∂
∂
∂
∂
∂
∂
∂
∂
+++=
=⋅
+
+
+
+
=⋅
⋅+⋅=
На основе примера 1 получаем
.6)6( ;12)6(
;6)6( ;0)2(
22
3
3
2
2
3
22
2
3
3
3
3
xyx
y
z
xyxy
yx
z
yxy
yx
z
y
x
z
yy
xx
=
′
==
′
=
=
′
==
′
=
∂
∂
∂∂
∂
∂∂
∂
∂
∂
Отсюда
322223
)(6)(123)(63 dyxdyxydxdydxyzd +⋅+⋅= .
Замечание. Дифференциалы высших порядков, вообще говоря, не обладают
свойством инвариантности их формы. Это имеет место уже для функций одной
переменной. Однако, если x
1
, ..., x
m
являются линейными функциями
переменных t
1
, ..., t
k
, то высшие дифференциалы можно вычислять по тем же
самым формулам, которые мы только что рассмотрели. При этом, если
ik
k
iii
ttx
βαα
+++=
)(
1
)1(
... (
i
α
(
- константы),
i
k
i
βα
,,...,
)()1
то
(i = 1,...,m).
k
k
iii
dtdtdx
)(
1
)1(
...
αα
++=
В частности, если все x
i
зависят от одной переменной t, то в формулы для
дифференциалов надо подставлять
dx dt
ii
α
=
.
Это обстоятельство используется при доказательстве формулы Тейлора.
9.8. Формула Тейлора
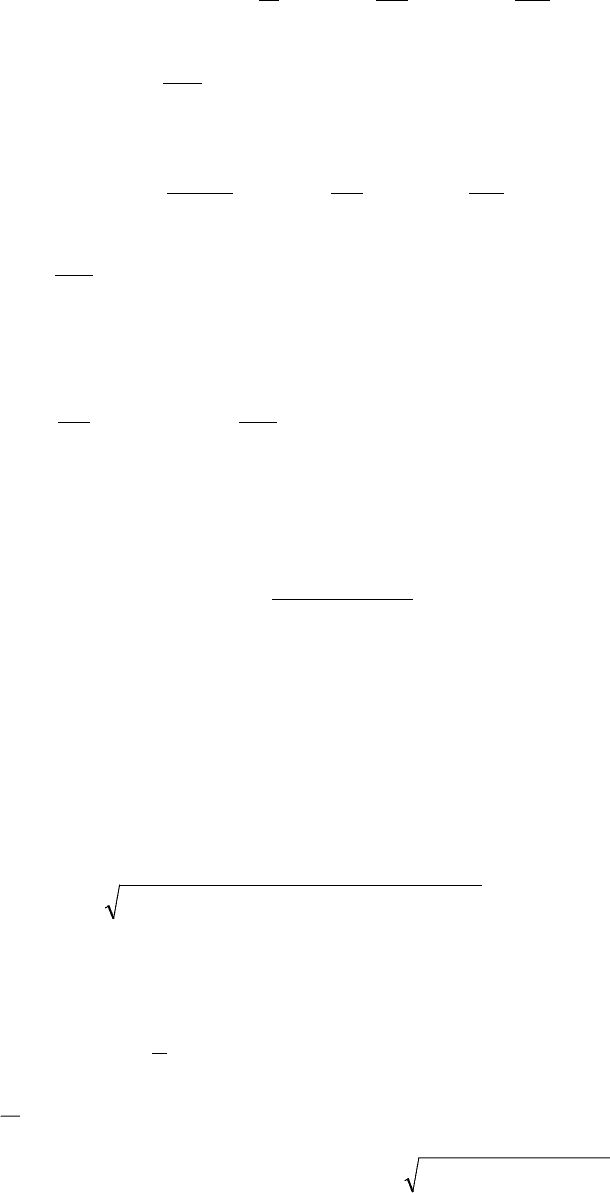
Пусть функция f(x
1
, ..., x
m
) задан и n+1 раз дифференцируема в некоторой
окрестности точки М
0
( ), тогда для всех точек М(х
00
1
,...,
m
xx
1
,...,х
m
) из этой
окрестности справедлива формула
),,..,(),...,()(
...)()(
!
1
),...,(),...,(
11
00
1
0
1
2
0
22
1
0
11
00
11
mnm
k
m
mm
n
k
mm
xxRxxf
x
xx
x
xx
x
xx
k
xxfxxf
+
=
+
−+
+−+−+=
∑
∂
∂
∂
∂
∂
∂
где
,10 )),(),...,(()(
...)()(
)!1(
1
),...,(
000
11
0
1
1
0
2
0
22
1
0
1111
<<−+−+⋅
−+
+−+−
+
=
+
+
θθθ
∂
∂
∂
∂
∂
∂
mmm
n
m
mm
mn
xxxxxxf
x
xx
x
xx
x
xx
n
xxR
где
θ зависит, вообще говоря, от М(х
1
,...,х
m
).
Заметим, что в принятых нами символических обозначениях
),,...,(),...,()(...)(
00
1
00
1
0
1
0
11
m
k
m
k
m
mm
xxfdxxf
x
xx
x
xx =
−++−
∂
∂
∂
∂
причем
. )(,..., ,
00
222
0
111
mmm
xxdxxxdxxxdx −=−=−=
Таким образом, формула Тейлора может быть записана более компактно:
,),...,(
!
),...,(
),...,(),...,(
1
11
00
1
00
11
∑
=
+
++=
n
k
mn
m
k
mm
xxR
k
xxfd
xxfxxf
где
))(),...,((),...,(
000
11
0
1
1
11
mmm
n
mn
xxxxxxfdxxR −+−+=
+
+
θθ
.
Замечание 1. При более слабых предположениях, а именно, если f(x
1
,...,x
m
)
дифференцируема (n-1) раз в окрестности т.М
0
и n раз в самой точке М
0
, для
остаточного члена в формуле Тейлора R
n+1
(x
1
,...,x
m
) справедливо представление
R
n+1
(x
1
,...,x
m
) = 0(ρ
n
) (форма Пеано), где
2020
22
20
11
)(...)()(
mm
xxxxxx −++−+−=
ρ
Замечание 2. В случае двух переменных (u=f(x,y)) формула Тейлора второго
порядка в развернутом виде записывается следующим образом:
+
−⋅
′
+−⋅
′
+= )(),()(),(
!1
1
),(),(
00000000
yyyxfxxyxfyxfyxf
yx
.)()( ),(0)(),(
)()(),(2)(),(
!2
1
2
0
2
0
22
000
0000
2
000
yyxx‹ŠŒyyyxf
yyxxyxfxxyxf
yy
xyxx
−+−=+
−⋅
″
+
+−⋅−⋅
″
+−⋅
″
+
ρρ
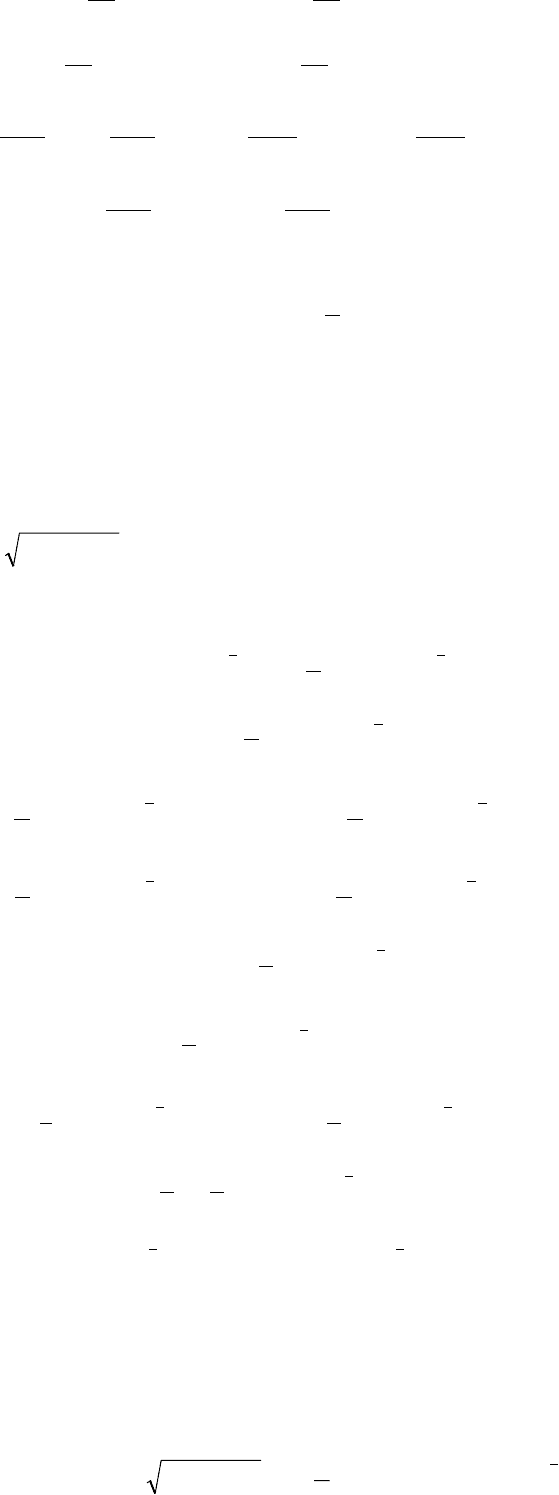
Пример 1. Разложить по формуле Тейлора второго порядка в окрестности т. (1,1)
функцию f(x,y) = x
3
- 3xy
3
+ xy - y
2
+ 6x - y + 1
(
())
()
22
22
222
2
2
2
2
2
2
2
2
2
2
2
2
2
32
)1()1(0
)1(10)1)(1(8)1(3)1(11)1(74
)1()1(0)1(20
)1()1(82)1(6
2
1
)1(11)1(74),(
;41161131)1,1(
;20218)1,1( ;218
;819)1,1( ;19 ;6)1,1( ;6
;111219)1,1( ;129
;76133)1,1( ;633
−+−+
+−−−−−−+−−−+=
=−+−⋅+−⋅−
−−⋅−⋅⋅−−⋅+−⋅−−⋅+=
=+−+−+−=
−=−−=−−=
−=+−=+−===
−=−−+−=−−+−=
=++−=++−=
yx
yyxxyx
yxy
yxxyxyxf
f
y
f
xy
y
f
yx
f
y
yx
f
x
f
x
x
f
y
f
yxxy
y
f
x
f
yyx
x
f
∂
∂
∂
∂
∂∂
∂
∂∂
∂
∂
∂
∂
∂
∂
∂
∂
∂
∂
∂
∂
∂
Пример 2. Разложить по формуле Маклорена до членов третьего порядка
функцию
22
1 yxu −−= (по формуле Тейлора с центром в т.М
0
(0,0)).
Последовательно находим дифференциалы функции u до третьего порядка
включительно.
);22()1(
2
1
;)1(),(
2
1
22
2
1
22
ydyxdxyxduyxyxu −−−−=−−=
−
).)(2)(2()1(
2
1
)22()1(
4
1
)22()1(
2
1
)22()1(
2
1
)22()1(
2
1
)(
22
2
1
222
2
3
22
2
1
22
2
1
22
2
1
222
dydxyxydyxdxyx
ydyxdxdyxydyxdxyxd
ydyxdxyxddudud
−−−−+−−−−−=
=−−−−+−−⋅
−−=
=
−−−−==
−−
−−
−
()
()
()
.)()()()1(3)()1(3
)(2)(2)22()1(
2
1
2
1
)(2)(2
)22(2)1(
4
1
)22()1(
8
3
))(2)(2()1(
2
1
)22()1(
4
1
)(
22
2
3
223
2
5
22
22
2
3
2222
2
3
223
2
5
22
22
2
1
22
2
2
3
2223
dydxydyxdxyxydyxdxyx
dydxydyxdxyxdydx
ydyxdxyxydyxdxyx
dydxyxd
ydyxdxyxduddud
++−−−+−−−=
=−−−−−−⋅
−⋅+−−⋅
⋅−−⋅−−−−−−−=
=
−−−−+
+
−−−−−==
−−
−
−−
−
−
Полагая здесь x=y=0, dx=x, dy=y, получаем
u(0,0)=1; du(0,0)=0; d
2
u(0,0)= -(x
2
+y
2
); d
3
u=0
и
u(x,y)
+++−=−−≡
2
3
222222
)(0)(
2
1
11 yxyxyx
.
9.9. Неявные функции
Пусть задано уравнение f(x,y)=0, где f - дифференцируемая функция
переменных х и у. Возникает вопрос о том, при каких условиях это
функциональное уравнение однозначно разрешимо относительно у, т.е.
однозначно определяет явную функцию y=
ϕ(x), и следующий вопрос о том, при
каких условиях эта явная функция непрерывна и дифференцируема.
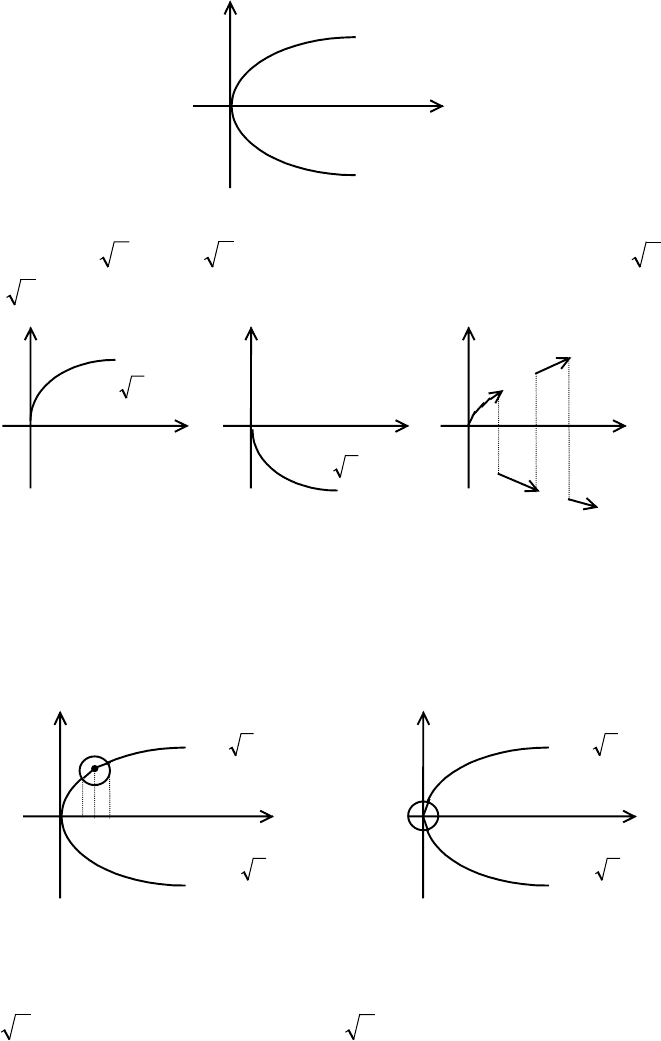
Трудность этих вопросов видна уже на простейшем примере уравнения y
2
-
x = 0. Это уравнение
y
y
2
= x
0 x
определяет при х
≥0 бесконечно много явных функций.
Например,
xyxy −=+= , и любая функция, равная + x для одних
значений х, и - x для других значений.
y y y
y =
x
0 x 0 x 0 x
y=-
x
Вопрос 1. При каких условиях существует единственная явная функция
удовлетворяющая уравнению y
2
= x. Фиксируем точку N
0
(x
0
,y
0
) на кривой y
2
-x=0,
отличную от начала координат.
Очевидно, что часть кривой, лежащая в достаточно малой окрестности
точки N
0
, однозначно проектируется на ось Ох.
y y
yx=
yx=
N
0
(x
0
,y
0
)
0 [ x
0
x N
1
(0,0) x
yx=−
yx=−
Аналитически это означает, что если рассматривать функцию f(x,y)=y
2
- x
только в этой достаточно малой окрестности точки N
0
, то уравнение f(x,y)=0
однозначно разрешимо относительно у и определяет единственную явную
функцию
xy += для у
0
>0 (см. рис.) и xy −= для у
0
<0.
Если мы теперь рассмотрим точку N
1
(0,0), то часть кривой
y
2
-x=0 не однозначно проектируется на ось ОХ (см. рис.). Аналитически это
означает, что если рассматривать функцию f(x,y)=y
2
-x в любой окрестности т.
N
1
(0,0), то уравнение f(x,y)=y
2
-x=0 не является однозначно разрешимым
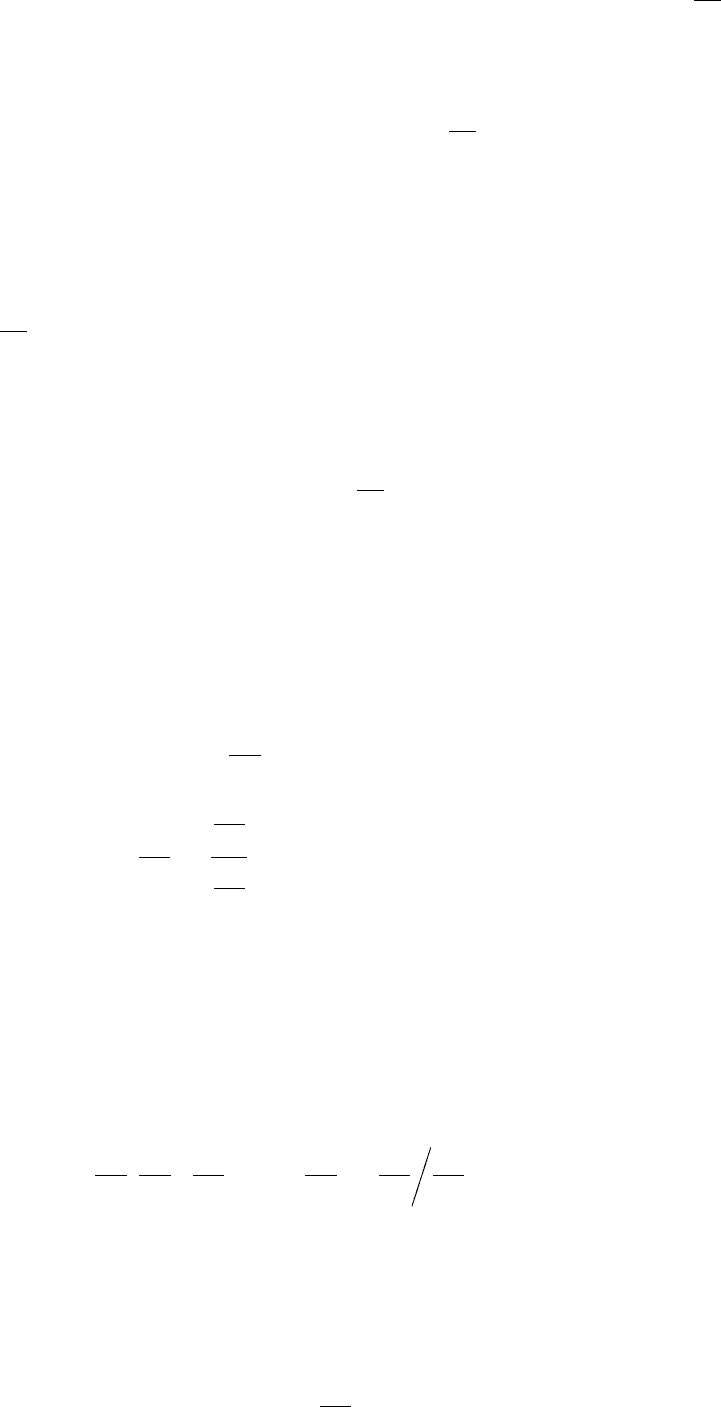
относительно у. Заметим, что в этой точке N
1
(0,0) частная производная y
y
f
2=
∂
∂
функции f(x,y)=y
2
-x обращается в нуль. В общем случае это обстоятельство имеет
принципиальное значение: для однозначной разрешимости уравнения f(x,y)=0 в
окрестности т. (х
0
,у
0
) относительно у требуется, чтобы 0),(
00
≠yx
y
f
∂
∂
.
В случае, когда рассматривается уравнение вида F(u, x
1
, ..., x
m
)=0, имеют
место те же трудности, что и в случае одной переменной: для однозначной
разрешимости этого уравнения относительно u нужно рассматривать функцию
F(u, x
1
, ..., x
m
) в окрестности точки (для которой , и
требовать, чтобы
),...,,(
00
100
m
xxuN 0),...,,(
00
10
=
m
xxuF
0≠
u
f
∂
∂
в т. N
0
.
Формулировка теоремы о неявной функции имеет вид.
Теорема. Пусть функция F(u, x
1
, ..., x
m
) дифференцируема в некоторой
окрестности точки
, причем
100
100
),...,,(
+
∈
m
m
RxxuN 0)(
0
≠N
u
f
∂
∂
и . Тогда
для любого достаточно малого
ε>0 существует такая окрестность точки
, в которой определена (единственная) функция u=u(x
0),...,,(
00
10
=
m
xxuF
m
m
RxxM ∈),...,(
00
10
1
, ..., x
m
)
удовлетворяющая условию
u-u
0
<ε и являющаяся решением уравнения F(u, x
1
,
..., x
m
)=0.
Эта функция u=u(x
1
, ..., x
m
) непрерывна и дифференцируема в окрестности т. М
0
(см. [4] (гл. 14, п.1, стр. 663)).
Замечание 1. Частные производные
i
x
u
∂
∂
вычисляются по формулам
u
F
x
F
x
u
i
i
∂
∂
∂
∂
∂
∂
−= (i = 1, ..., m).
Эти формулы получаются следующим образом: подставим неявную
функцию u=u(x
1
, ..., x
m
) в уравнение F(u, x
1
, ..., x
m
)=0
получим
F(u(x
1
, ..., x
m
), x
1
, ..., x
m
)=0.
Это равенство является тождеством по x
1
, ..., x
m
. Вычислим частные
производные от обеих частей этого равенства по x
i
, используя теорему о
производной сложной функции,
u
F
x
F
x
u
x
F
x
u
u
F
i
iii
∂
∂
∂
∂
∂
∂
∂
∂
∂
∂
∂
∂
−=⇒=+⋅ 0
Аналогично можно найти и высшие k-е производные неявной функции, если
функция F(u, x
1
, ..., x
m
) дифференцируема k раз.
Пример 1. Найти частные производные функции z, заданной неявно:
F
≡ z
3
+ x
5
+ y
5
- 2xyz + 2x - 4 = 0.
Уравнение разрешимо относительно z, если
0≠
z
F
∂
∂
, т.е. 3z
2
- 2xy ≠ 0.
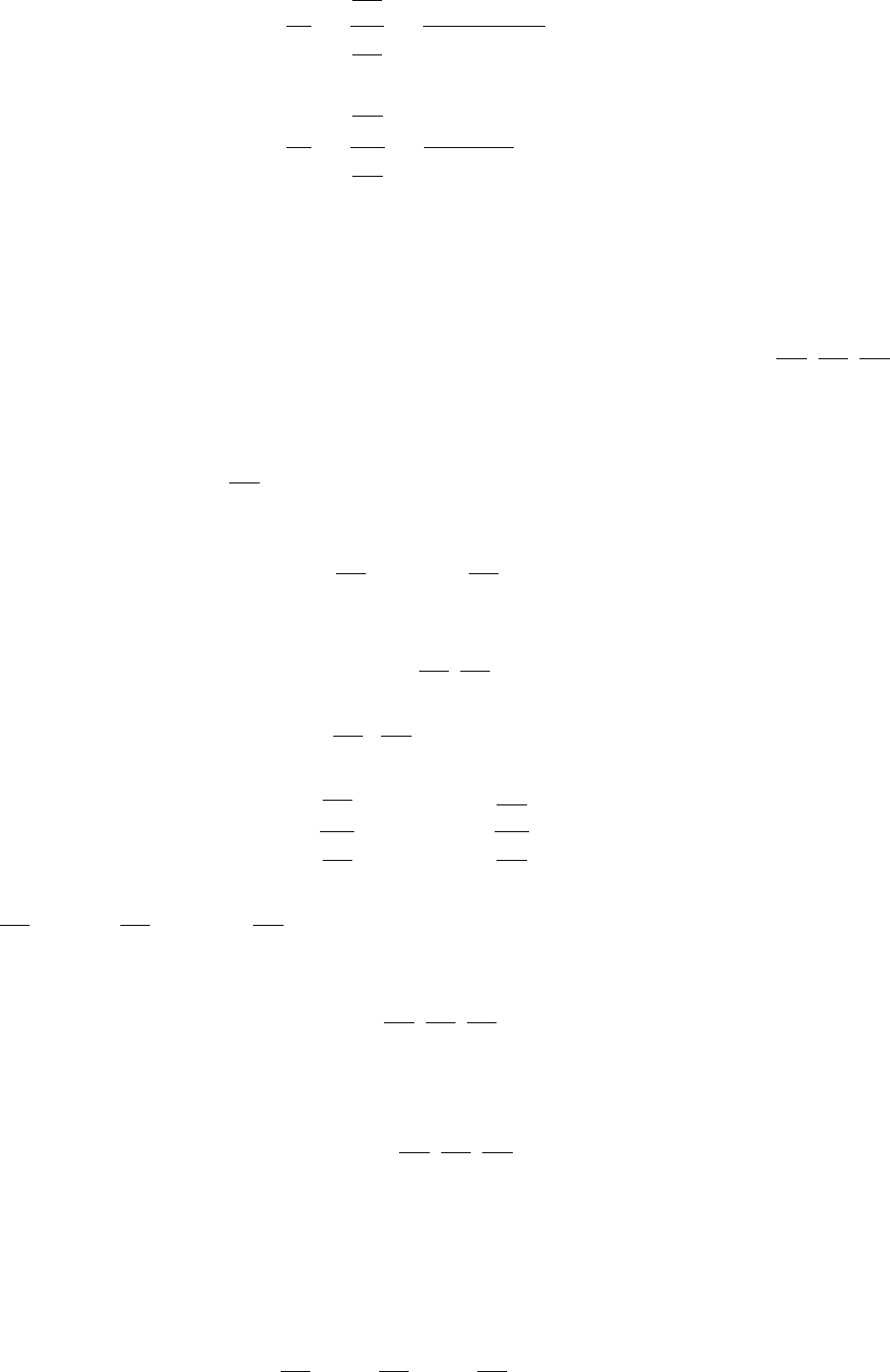
.
23
25
;
23
225
2
4
2
4
xyz
xzy
z
F
y
F
y
z
xyz
yzx
z
F
x
F
x
z
−
−
−=−=
−
+−
−=−=
∂
∂
∂
∂
∂
∂
∂
∂
∂
∂
∂
∂
Теорема о неявной функции имеет следующие геометрические приложения:
Пусть задана поверхность уравнением F(x,y,z)=0.
Требуется написать уравнение касательной плоскости к этой поверхности и
вычислить координаты нормального вектора к этой поверхности в некоторой
точке (x
0
,y
0
,z
0
). Предположим, что одна из частных производных
z
F
y
F
x
F
∂
∂
∂
∂
∂
∂
,,
отлична от нуля в этой точке. Это значит, что одна из переменных может быть
выражена как функция двух других.
Пусть, например,
0≠
x
F
∂
∂
, тогда x = ϕ(y,z), а для такой функции, уравнение
касательной плоскости имеет вид
).()(
000
zz
z
yy
y
xx −⋅+−⋅=−
∂
∂ϕ
∂
∂ϕ
Нормальный вектор имеет координаты:
−=
zy
n
∂
∂ϕ
∂
∂ϕ
;;1
r
Подставляя сюда выражения для
zy
∂
∂ϕ
∂
∂ϕ
, , получим
),()(
000
zz
x
F
z
F
yy
x
F
y
F
xx −⋅
−+−⋅
−=−
∂
∂
∂
∂
∂
∂
∂
∂
или
0)()()(
000
=−⋅+−⋅+−⋅ zz
z
F
yy
y
F
››
x
F
∂
∂
∂
∂
∂
∂
, а в качестве нормального вектора к
поверхности можем взять следующий:
=
z
F
y
F
x
F
n
∂
∂
∂
∂
∂
∂
;;
1
r
Замечание: Если рассматривать поверхность уровня F(x,y,z)=C функции
u=F(x,y,z), то мы получим, что
≡
z
F
y
F
x
F
gradu
∂
∂
∂
∂
∂
∂
;; ортогонален поверхности
уровня.
Пример 2. Дана поверхность x
2
+4y
2
+2z
2
= 7. Написать уравнения касательных
плоскостей к этой поверхности, которые параллельны плоскости x+y+z=1
Здесь F(x,y,z) = x
2
+4y
2
+2z
2
- 7,
z
z
F
y
y
F
x
x
F
4 ;8 ;2 ===
∂
∂
∂
∂
∂
∂
.
Нормальный вектор к поверхности имеет координаты
{}
zyxn 4,8,2=
r

он должен быть коллинеарен нормальному вектору к заданной плоскости, т.е.
вектору {1,1,1}.
Отсюда
1
4
1
8
1
2 zyx
==
Решив систему уравнений
, находим координаты точек касания
==
=++
zyx
zyx
482
724
222
−−−
1;
2
1
;2 1;
2
1
;2
.
Касательные плоскости имеют уравнения:
.05,3 ;0)1(4)
2
1
(4)2(4
05,3 ;0)1(4)
2
1
(4)2(4
=+++=+−+−+−
=−++=−+−+−
zyxzyx
zyxzyx
9.10. Экстремум функции нескольких переменных
Определение 1. Пусть функция f(x
1
, ..., x
m
) определена на множестве
{}
.
Внутренняя точка
называется точкой локального максимума
(минимума), если существует такая окрестность U(M
m
RM ⊂
{}
MxxM
m
∈),...,(
00
10
0
) точки М
0
, что для всех
М(х
1
, ..., х
m
) ∈ U(M
0
) выполняется неравенство f(M) ≤ f(M
0
) [f(M) ≥ f(M
0
)].
Определение 2. Точка М
0
локального максимума или локального минимума
называется точкой локального экстремума.
Теорема (Необходимое условие локального экстремума). Пусть функция f(x
1
, ...,
x
m
) определена в некоторой окрестности т. , дифференцируема в точке
М
),...,(
10
m
xxM
00
0
, и имеет в этой точке локальный экстремум, тогда все частные производные
первого порядка функции f в т. М
0
равны нулю:
).0)( ( 0)(...)(
000
1
==== MdfèëèM
x
f
M
x
f
m
∂
∂
∂
∂
Доказательство: Докажем, что
0)(
0
1
=M
x
f
∂
∂
. Если точка является
локальным экстремумом функции f(x
),...,(
00
10
m
xxM
0
1
x
1
, ..., x
m
), то, очевидно, точка является
точкой локального экстремума функции
одной переменной x),...,,
21
m
xx(xf
00
1
. По
теореме Ферма получаем (см. рис. 1)
.0
),...,,(
)(
0
11
1
00
21
0
1
==
=xx
m
dx
xxxdf
M
x
f
∂
∂
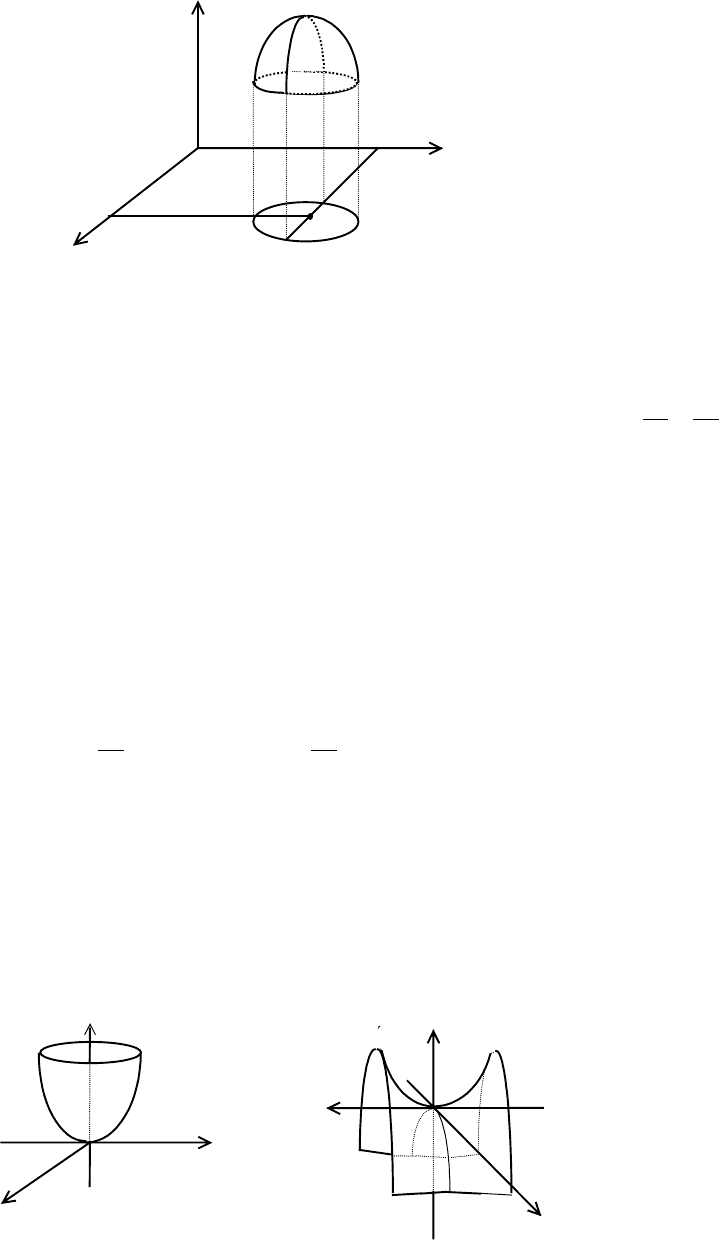
u
x
2
0
2
x
1
0
x
1
M
0
( x
1
0
, x
2
0
)
x
Рис.1
Пример 1. Найдем точки экстремума функции z = x
2
+ y
2
. Точки экстремума в
силу доказанного находятся среди тех, для которых
0==
y
z
x
z
∂
∂
∂
∂
,
т.е.
. Система имеет единственное решение (0,0). Убедимся, что в этой
точке действительно функция имеет экстремум. Для этого заметим, что в т. (0,0)
z=0, во всех других точках z=x
=
=
02
02
y
x
2
+y
2
>0. Поэтому точка (0,0) является не только
точкой локального минимума (но и “глобального” минимума) (см. рис.2).
Пример 2. Исследуем точки экстремума функции z=x
2
-y
2
.
Поступая аналогично предыдущему случаю, находим
02 == x
x
z
∂
∂
; 02 =−= y
y
z
∂
∂
.
Решение (0,0), т.е. если функция z=x
2
-y
2
имеет экстремум, то он может быть
только в этой точке.
Исследуем, имеет ли функция z=x
2
-y
2
в точке (0,0) локальный экстремум. В
т. (0,0) z=0. Однако здесь при у=0 и любых х
≠0 z=x
2
>0, а при х=0 и любом у≠0 z=-
у
2
<0. Поэтому точка (0,0) не является точкой локального экстремума функции
z=x
2
-y
2
вообще не имеет точек экстремума.
(см. рис.3).
z z
x
0 y
x y
Рис.2 Рис.3
Точки, в которых обращаются в нуль все частные производные первого
порядка функции f(x
1
, ..., x
m
), называются стационарными точками этой функции.
Примеры 1 и 2 показывают, что в каждой стационарной точке требуется
дополнительное исследование на экстремум, т.е. нужны достаточные условия
экстремума.
Прежде, чем их сформулировать, напомним некоторые сведения из теории
квадратичных форм:
