Никишкин В.А., Малахов А.Н., Максюков Н.И. Высшая математика
Подождите немного. Документ загружается.

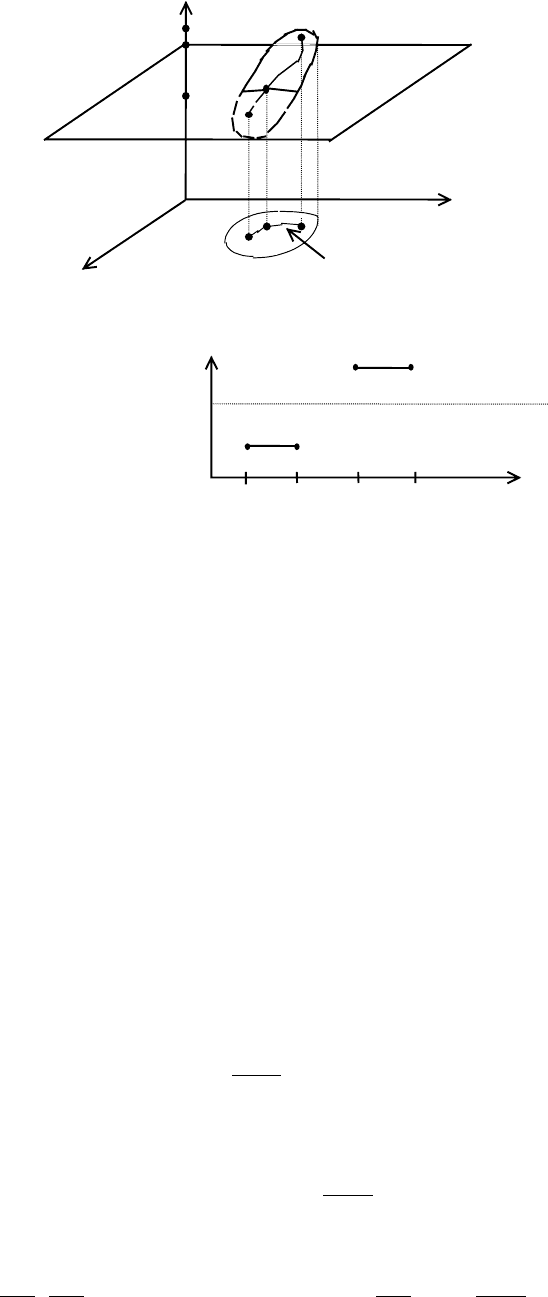
Теорема. Пусть функция u=f(M) непрерывна на связном множестве {M}. Тогда
для любых точек А, В
∈{M} и для любой кривой, L, соединяющей эти точки и
лежащей в {M}, найдется точка на этой кривой, в которой функция принимает
любое заданное промежуточное значение между f(A) и f(B).
u
f(B)
C
f(A)
≤
C
≤
f(B)
f(A)
K
∈
L, f(K)=C
y
A B
x L
K
Условие связности существенно уже в одномерном случае:
u
c
5. Теоремы Вейерштрасса.
Теорема 1. Функция, непрерывная на ограниченном замкнутом множестве,
ограничена на этом множестве.
Теорема 2. Функция, непрерывная на ограниченном замкнутом множестве,
достигает на этом множестве своих точных верхней и нижней граней. Для
неограниченных или не замкнутых множеств эти утверждения неверны уже в
одномерном случае.
9.6. Дифференцируемость функций нескольких переменных
9.6.1. Частные производные функции нескольких переменных
Пусть М(х
1
, х
2
, ..., х
m
) внутренняя точка области определения функции
u=f(x
1
, ..., x
m
). Пусть ∆x
k
- приращение k-ой координаты в данной фиксированной
т.М, ему соответствует частное приращение функции
∆x
k
u ≡ f(x
1
, ..., x
k-1
, x
k
+∆x
k
, x
k+1
, ..., x
m
) - f(x
1
, ..., x
m
).
Рассмотрим отношение
k
k
x
ux
∆
∆
, которое зависит от ∆x
k
и определено при всех
достаточно малых
∆x
k
, отличных от нуля.
Определение 1. Если существует
k
k
x
x
ux
∆
∆
→∆ 0
lim , то он называется частной производной
функции u=f(x
1
, ..., x
m
) в т. М(x
1
, ..., x
m
) по аргументу x
k
и обозначается одним из
символов:
k
x
f , , ,
′′
k
x
kk
u
x
f
x
u
∂
∂
∂
∂
. Таким образом,
k
k
x
k
x
ux
x
u
∆
∆
=
→∆ 0
lim
∂
∂
.
Замечание. Так как изменяется только x
k
+ ∆x
k
, т.е. k-я координата аргумента
функции f, то частная производная
k
x
u
∂
∂
является обыкновенной производной
функции f как функции только k-й переменной (при фиксированных остальных
переменных). Это позволяет вычислить частные производные по одной из
переменных по обычным формулам дифференцирования, если зафиксировать все
остальные переменные.
Пример 1. u = x
2
+ 3xy - y
x
u
∂
∂
вычисляем при условии, что y = const
yx
x
u
32 +=
∂
∂
y
u
∂
∂
вычисляем при условии, что x = const
13 −= x
y
u
∂
∂
Пример 2.
22
yx
eu
−
=
)2(
22
xe
x
u
yx
+⋅=
−
∂
∂
(при фиксированном у применима обычная теорема о
производной сложной функции)
Аналогично
)2(
22
ye
y
u
yx
−⋅=
−
∂
∂
Выясним теперь, насколько полную информацию дают частные
производные функции в данной точке о поведении функции в окрестности этой
точки.
Сразу отметим, что частные производные в т.М
0
могут дать информацию о
поведении функции только на прямых, проходящих через т.М
0
и параллельных
координатным осям.
М
0
Конечно, этой информации совсем не достаточно, чтобы судить о
поведении функции в целой окрестности т.М
0
(и, в частности, на других лучах,
проходящих через т.М
0
).
Пример 3. Функции
==
≠+
+
=
.0 ïðè 0
0 ïðè
44
44
22
yx
yx
yx
yx
u
показывает, что частные
производные ее
0
0
0
0)(
0)(
lim
)0,()0,(
lim
44
22
44
22
00
)0,(
=
∆
+
⋅
−
+∆+
⋅∆+
=
∆
−∆+
=
→∆→∆
x
x
x
xx
xx
x
xuxxu
x
u
xx
x
∂
∂
(аналогично
0
),0(
≡
y
y
u
∂
∂
)

существуют и обращаются в нуль не только в т. (0,0), но и всюду на
координатных осях, а сама функция не имеет в т. (0,0) предела (см. тему 4).
Заметим, что в одномерном случае из существования производной следовала
непрерывность функции.
Таким образом, мы приходим к необходимости ввести более сильное
условие, чем существование частных производных, чтобы оно было аналогом
дифференцируемости функции одной переменной. Это условие должно быть
связано с полным приращением функции в точке.
9.6.2. Дифференцируемость функции нескольких переменных
Определение 2. Функция u=f(x
1
, ..., x
m
) называется дифференцируемой в точке
M(x
1
, ..., x
m
), если ее полное приращение в этой точке может быть представлено в
виде
f(x
1
+∆x
1
, ..., x
m
+∆x
m
) - f(x
1
, ..., x
m
) ≡
≡ ∆u = A
1
∆x
1
+ A
2
∆x
2
+ ... + A
m
∆x
m
+ α
1
∆x
1
+ ... + α
m
∆x
m
,
где А
1
, А
2
, ..., А
m
- некоторое, не зависящие от ∆x
1
, ..., ∆x
m
, числа,
а
α
1
, α
2
, ..., α
m
- бесконечно малые при ∆x
1
→0, ..., ∆x
m
→0 функции, равные 0 при
∆x
1
=∆x
2
=...=∆x
m
=0.
Если положить
22
1
...
m
xx ∆++∆=
ρ
, то условие дифференцируемости может
быть записано в виде:
∆u = A
1
∆x
1
+ A
2
∆x
2
+ ... + A
m
∆x
m
+ 0(ρ) (1)
Оба представления эквивалентны и означают, что приращение функции
представимо в виде линейной части (по ∆x
1
, ..., ∆x
m
) и членов более высокого
порядка (по
∆x
1
, ..., ∆x
m
или ρ).
Теорема 1. Если функция u=f(x
1
, ..., x
m
) дифференцируема в точке
M(x
1
, ..., x
m
), то в этой точке существуют частные производные по всем
аргументам, причем
i
i
A
x
u
=
∂
∂
, где А
i
определяются из условия
дифференцируемости.
Доказательство: Положим в условии дифференцируемости все приращения,
кроме
∆x
k
, равными нулю, тогда для частного приращения справедливо
представление
∆x
k
u = A
k
∆x
k
+ α
k
⋅∆x
k
Отсюда
kk
k
k
A
x
ux
α
+=
∆
∆
и т.к. α
k
→ 0 при ∆x
k
→ 0, то
k
kk
k
x
A
x
u
x
ux
k
==
∆
∆
=
→∆
∂
∂
0
lim .
Следствие. Условие дифференцируемости функции в данной точке можно
записать в виде:
)(0...
1
1
ρ
∂
∂
∂
∂
+∆=++∆=∆
m
m
x
x
u
x
x
u
u
Замечание 1. Существование частных производных в точке не достаточно для
дифференцируемости функции в этой точке.
Пример 4.
5
xyu =
0
000)0,0(
lim
)0,0()0,0(
lim)0,0(
5
5
00
=
∆
⋅−⋅∆+
=
∆
−∆+
=
′
→∆→∆
x
x
x
uxu
u
xx
x
0
00)0(0
lim
)0,0()0;0(
lim)0,0(
5
5
00
=
∆
⋅−∆+⋅
=
∆
−∆+
=
′
→∆→∆
y
y
y
uyu
u
yy
y
Покажем, что эта функция не дифференцируема в т. (0,0). Этого следует
ожидать, т.к. порядок приращения функции в нуле равен
5
2
(
5
yx ∆⋅∆=u ), а в
условии дифференцируемости требуется, чтобы порядок приращения был не
ниже первого.
Предположим, что приращение функции представляется в виде
∆u = 0⋅∆x + 0⋅∆y + 0(ρ)
Это означает, что
)(0
5
ρ
=∆⋅∆ yx ;
22
)()( yx ∆+∆=
ρ
т.е. должно выполняться условие
0
)()(
lim
22
5
0,0
=
∆+∆
∆⋅∆
→∆→∆
yx
yx
yx
Положив
∆x = ∆y, получим
∞=∆=
∆
∆
=
∆+∆
∆⋅∆
−
→∆→∆
∆=∆
→∆
→∆
5
3
0
2
5
2
0
22
5
0
0
2
1
lim
)(2
)(
lim
)()(
lim x
x
x
yx
yx
xx
yx
y
x
Отсюда следует, что
5
yx ∆⋅∆ не является 0(ρ), т.е. функция не является
дифференцируемой в нуле.
Замечание 2. Из дифференцируемости функции в точке следует ее
непрерывность в этой точке. Действительно, из представления (1) следует,
что
. 0lim
0
...
0
1
=∆
→∆
→∆
x
m
x
x
Обратное неверно даже в одномерном случае.
В предыдущем примере функция не является дифференцируемой, но
является непрерывной. Действительно
()
0
22
5
1
2
5
1
22
5
1
5
→
=
∆+∆
≤∆⋅∆=∆⋅∆
ρ
yx
yxyx
при 0→
ρ
.
Здесь использовано неравенство
2
22
ba
ab
+
≤
, которое, очевидно, следует из
неравенства (а-b)
2
≥ 0.
9.6.3. Достаточное условие дифференцируемости
Пусть функция u = f(x
1
, ..., x
m
) имеет частные производные по всем
аргументам в некоторой окрестности точки
, и эти частные
производные непрерывны в самой точке М
),...,(
00
10
m
xxM
0
, тогда эта функция дифференцируема
в т. М
0
. Принимая утверждение без доказательства, мы только отметим, что здесь
частные производные рассматриваются как функции m переменных
i
x
f
∂
∂
(x
1
, ..., x
m
)

в окрестности точки М
0
, причем эти функции непрерывны по совокупности
переменных в т. М
0
(и противоречия с примером 3 этой темы нет).
9.6.4. Геометрический смысл условия дифференцируемости функции двух
переменных u=f(x,y)
Определение 1. Касательной плоскостью к графику функции u=f(x,y) в точке (х
0
,
y
0
, f(x
0
,y
0
)) называется такая плоскость, что разность ее апликаты и значения
функции f(x,y) является величиной, бесконечно малой по сравнению с
ρ при ρ→0,
где
2
0
2
0
)()( yyxx −+−=
ρ
Пусть u
0
= f(x
0
,y
0
), u = f(x,y), тогда условие дифференцируемости в т. (x
0
,y
0
)
этой функции записывается в виде
u - u
0
= A(x-x
0
)+B(y-y
0
)+0(ρ),
или
u = u
0
+ A(x-x
0
)+B(y-y
0
)+0(ρ).
Рассмотрим следующую плоскость
U-u
0
= A(x-x
0
) + B(y-y
0
)
(U - откладывается на той же оси Оz, что и u), тогда ее апликата U определяется
равенством
U = u
0
+ A(x-x
0
) + B(y-y
0
),
и разность
U-u = u
0
+ A(x-x
0
) + B(y-y
0
) - (u
0
+A(x-x
0
) + B(y-y
0
) + 0(ρ)) = 0(ρ).
Таким образом, если функция u=f(x,y) дифференцируема в т. (x
0
,y
0
), то
график этой функции в соответствующей точке (x
0
,y
0
, f(x
0
,y
0
)) имеет касательную
плоскость, задаваемую уравнением
z - f(x
0
,y
0
) = )(),()(),(
000000
yyyx
x
f
xxyx
x
f
−⋅+−⋅
∂
∂
∂
∂
Из аналитической геометрии известно, что нормальный вектор к этой
касательной плоскости имеет координаты
−1);,();,(
0000
yx
y
f
yx
x
f
∂
∂
∂
∂
.
Уравнения нормали к касательной плоскости в т. (x
0
,y
0
, f(x
0
,y
0
)) имеют вид:
1
),(
),(),(
00
00
0
00
0
−
−
=
−
=
− yxfz
yx
y
f
yy
yx
x
f
xx
∂
∂
∂
∂
Замечание. Касательная плоскость может быть определена также следующим
эквивалентным образом.
Определение 2. Плоскость П, проходящая через точку N
0
поверхности,
называется касательной плоскостью в этой точке, если угол между этой
плоскостью и секущей, проходящей через точку N
0
и любую точку N
1
поверхности, стремится к нулю, когда точка N
1
стремится к N
0
.
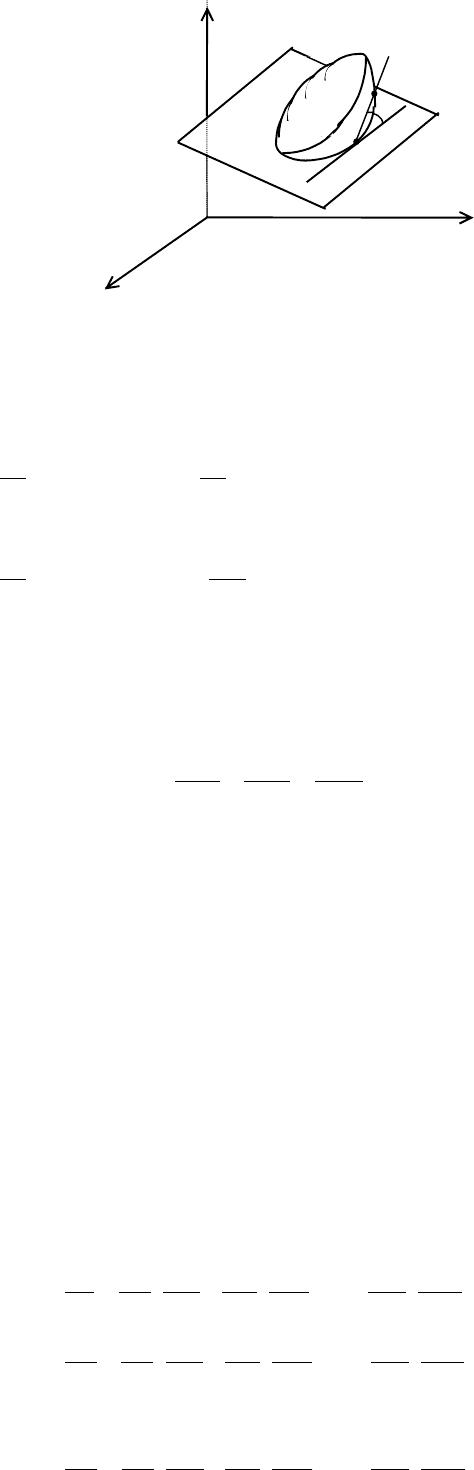
z
N
1
П
N
0
y
x
Пример 1. Дана функция z = 2x
2
- 3xy + 4y
2
- 2x + y
и точка (1,1). Написать уравнение касательной плоскости в соответствующей
точке графика этой функции, а также уравнения нормали.
6183)1,1( 183
.2)1,1( ;
1234)1,1( 234
=++−=++−=
=
−=−−=−−=
—
z
yx
y
z
z
x
z
yx
x
z
∂
∂
∂
∂
∂
∂
∂
∂
Уравнение касательной плоскости
z - 2 = -1
⋅(x-1) + 6⋅(y-1)
Уравнение нормали к графику функции в той же точке имеют вид:
1
2
6
1
1
1
−
−
=
−
=
−
−
zyx
9.6.5. Дифференцирование сложной функции
Пусть функция u = f(x
1
, ..., x
m
) и система функций
=
=
),...,(
...
),...,(
1
111
kmm
k
ttx
ttx
ϕ
ϕ
определяют сложную функцию, тогда справедлива следующая
Теорема. Пусть функции ϕ
i
(t
1
, ..., t
k
) (i = 1, ..., m) дифференцируемы в точке
, а функция u = f(x),...,(
00
10
k
ttA
,...,,(
0
2
0
10
xxM
((
11
tfu
ϕ
=
1
, ..., x
m
) дифференцируема в соответствующей точке
, где . Тогда сложная функция
дифференцируема в точке А
)
0
m
x
,...,
k
t
),...,(
00
1
0
kii
ttx
ϕ
=
)),...,(),...,
1 km
tt
ϕ
0
. Для частных
производных в т. А
0
справедливы следующие формулы:
,...
...
...
...
2
2
1
1
22
2
22
1
12
11
2
21
1
11
k
m
mkkk
m
m
m
m
tx
u
tx
u
tx
u
t
u
tx
u
tx
u
tx
u
t
u
tx
u
tx
u
tx
u
t
u
∂
∂ϕ
∂
∂
∂
∂ϕ
∂
∂
∂
∂ϕ
∂
∂
∂
∂
∂
∂ϕ
∂
∂
∂
∂ϕ
∂
∂
∂
∂ϕ
∂
∂
∂
∂
∂
∂ϕ
∂
∂
∂
∂ϕ
∂
∂
∂
∂ϕ
∂
∂
∂
∂
⋅++⋅+⋅=
⋅++⋅+⋅=
⋅++⋅+⋅=
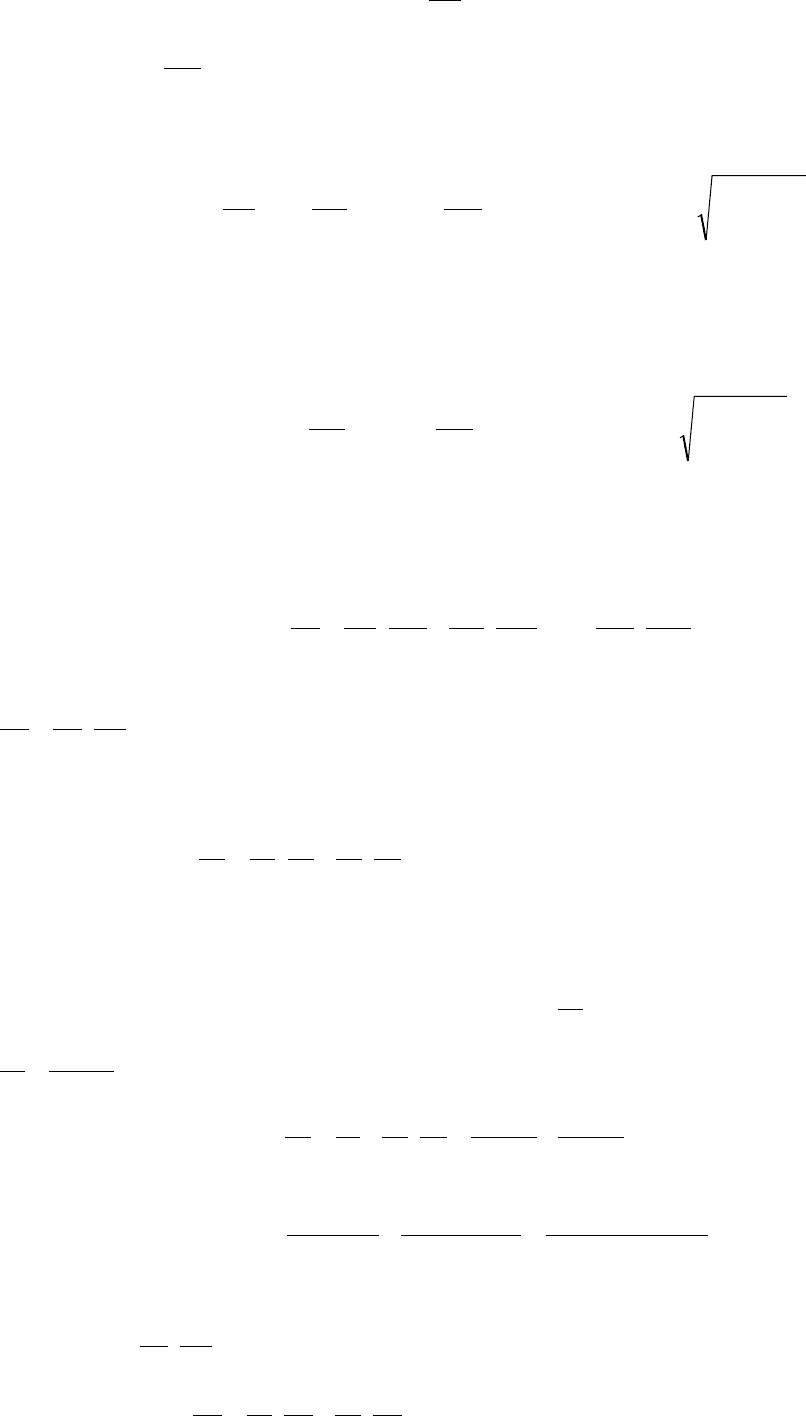
в которых частные производные ),...,1( mi
x
u
i
=
∂
∂
берутся в точке М
0
, а частные
производные
),...,1;,...,1( ksmi
t
s
i
==
∂
∂ϕ
берутся в точке А
0
.
Идея доказательства такая же, как и в одномерном случае.
В условие дифференцируемости внешней функции
),(0...
2
2
1
1
ρ
∂
∂
∂
∂
∂
∂
+∆++∆+∆=∆
m
m
x
x
u
x
x
u
x
x
u
u где ,)(
1
2
∑
=
∆=
m
i
i
x
ρ
подставляются не произвольные приращения переменных
∆x
1
, ..., ∆x
m
, а
приращения функции
),...,1( ),...,(
1
mitt
ki
=
ϕ
, соответствующие приращениям
аргументов
∆t
1
, ..., ∆t
k
. Эти приращения представимы в виде (следует из условия
дифференцируемости функций
)m,...,1)(,...,(
1
itt
ki
=
ϕ
)
),(0...
1
1
δ
∂
∂ϕ
∂
∂ϕ
ϕ
+∆++∆=∆=∆
k
k
ii
ii
t
t
t
t
x где .)(
1
2
∑
=
∆=
k
s
s
t
δ
Выделяя затем линейную часть
∆u относительно ∆t
1
, ..., ∆t
k
, мы получаем
выражения для частных производных сложной функции.
Заметим, что в случае, когда х
1
, ..., х
m
зависят только от одной переменной t,
производная по t сложной функции (обыкновенная) вычисляется по формуле
dt
d
x
u
dt
d
x
u
dt
d
x
u
dt
du
m
m
ϕ
∂
∂
ϕ
∂
∂
ϕ
∂
∂
⋅++⋅+⋅= ...
2
2
1
1
и если, кроме того, f зависит от одной переменной х, то формула принимает вид:
dt
d
dx
du
dt
du
ϕ
⋅= , т.е. совпадает с формулой для одномерного случая.
Пример 1.
, где x=cost, y=sint.
yx
ez
−
=
2
=⋅−⋅+−⋅⋅=⋅+⋅=
−−
tetxe
dt
dy
y
z
dt
dx
x
z
dt
dz
yxyx
cos)1()sin(2
22
∂
∂
∂
∂
здесь вместо х и у надо поставить их выражения через t
[]
[
]
1sin2coscos)sin(cos2
sincossincos
22
+−=−−=
−−
ttettte
tttt
.
Пример 2. , где x=sint. Вычислить )ln(
32
xtz +=
t
z
∂
∂
.
t
xtt
z
2
1
32
⋅
+
=
∂
∂
(Здесь t и x считаются независимыми переменными)
=⋅
+
+
+
=⋅+= t
xt
x
xt
t
dt
dx
x
z
t
z
dt
dz
cos
32
32
2
32
∂
∂
∂
∂
(Здесь вместо х необходимо подставить его выражение через t)
.
sin
cossin32
sin
cossin3
sin
2
32
2
32
2
32
tt
ttt
tt
tt
tt
t
+
⋅+
=
+
⋅
+
+
=
Пример 3. z = x
2
- y
2
, где x=t
1
⋅t
2
, y=t
1
-t .
2
2
Вычислить
.,
21
t
z
t
z
∂
∂
∂
∂
.222
)(221)2(2
1
2
2
2
21
2
212212
111
tttt
tttttytx
t
y
y
z
t
x
x
z
t
z
−+=
=−−⋅=⋅−+⋅=⋅+⋅=
∂
∂
∂
∂
∂
∂
∂
∂
∂
∂

.442
)(42)2()2(2
3
2212
2
1
2
21212121
222
ttttt
tttttttytx
t
y
y
z
t
x
x
z
t
z
−+=
=−+⋅=−⋅−+⋅=⋅+⋅=
∂
∂
∂
∂
∂
∂
∂
∂
∂
∂
9.6.6. Дифференциал функции нескольких переменных
Дифференциал функции нескольких переменных определяется как
линейная (относительно приращений аргументов) часть приращения
дифференцируемой функции
m
m
dx
x
u
dx
x
u
du
∂
∂
∂
∂
++= ...
1
1
,
где dx
i
≡ ∆x
i
(i=1, ..., m), если x
1
, ..., x
m
- независимые переменные.
Как и в случае одной переменной первый дифференциал обладает
свойством инвариантности его формы, т.е. выражение для первого
дифференциала имеет тот же вид и в случае, когда х
1
, ..., х
m
являются функциями
некоторых переменных t
1
, ..., t
k
. Свойство инвариантности формы первого
дифференциала позволяет установить следующие формулы
2
)(
)(
)( )(
v
dvuduv
v
u
d
duvdvuvud
dvduvud
constcducucd
⋅−⋅
=
⋅+⋅=⋅
±=±
=
⋅
=
⋅
Например, для дифференциала произведения рассуждаем следующим
образом. Рассмотрим функцию
ω = u⋅v двух переменных u, v. Дифференциал этой
функции равен
,dv
v
du
u
d ⋅+⋅=
∂
∂ω
∂
∂ω
ω
но
, u
v
v
u
=⋅=
∂
∂ω
∂
∂ω
следовательно,
d
ω = v⋅du + u⋅dv.
Пример 1.
u . Найти полный дифференциал функции
zy
x
−
=
2
dz
z
u
dy
y
u
dx
x
u
du
∂
∂
∂
∂
∂
∂
++=
(
)
()
()
)1(ln
2ln
)(
22
22
22
12
−⋅⋅=
′
=
⋅⋅=
′
=
⋅−=
′
=
−−
−−
−−−
xxx
z
u
yxxx
y
u
xzyx
x
u
zy
z
zy
zy
y
zy
zy
x
zy
∂
∂
∂
∂
∂
∂
Таким образом,
dzxxydyxxdxxzydu
zyzyzy
⋅⋅−⋅⋅+⋅−=
−−−−
ln2ln)(
222
12
Пример 2.
, где x=cost, y=t
yx
ez
+
=
2
2
. Вычислить дифференциал сложной функции.
Воспользуемся инвариантностью формы первого дифференциала
dy
y
z
dx
x
z
dz
∂
∂
∂
∂
+=

Здесь
.)2sin2(2)sin(cos2
2 ;1
sin ;cos22
22
cos2222
222
222
coscos
cos
cos
dtttetdtedtttedz
dttdyee
y
z
dttdxtexe
x
z
tt
tttt
ttyx
ttyx
−=⋅+−⋅=
⋅==⋅=
⋅−=⋅=⋅=
+
++
++
++
∂
∂
∂
∂
9.6.7. Производная по направлению. Градиент
Пусть задана функция двух переменных u=f(x,y) (для большего числа
переменных все аналогично), которая определена в окрестности т. (x
0
,y
0
) и
дифференцируема в этой точке. Мы будем рассматривать нашу функцию на
лучах, проходящих через т. (x
0
,y
0
). Луч задается начальной точкой и
направляющим единичным вектором
{
}
β
α
cos;cos
=
e
r
,
его параметрические уравнения имеют вид:
[
)
⋅+=
=+∞∈
⋅+=
β
αβ
α
cos
)sin(cos ,0
cos
0
0
tyy
t
txx
Подставляя эти выражения вместо аргументов функции u=f(x,y), мы
получим функцию одной переменной u(t): u = f(x
0
+ t⋅cosα, y
0
+ t⋅cosβ).
Если
0=
′
tt
u существует, то эту производную
0=t
dt
du
мы назовем производной
функции u=f(x,y) в точке (x
0
,y
0
) в направлении вектора (обозначение e
r
e
u
r
∂
∂
).
Используя формулы для производных сложной функции, получаем (для точки
t=0)
.cos),(cos),(),(
),(
)cos;cos(
000000
00
00
β
∂
∂
α
∂
∂
∂
∂
∂
∂
β
α
∂
∂
⋅+⋅=⋅+
+⋅=
⋅
+
⋅+
=
yx
y
f
yx
x
f
dt
dy
yx
y
f
dt
dx
yx
x
f
dt
tytxdf
e
u
r
Если ввести в рассмотрение вектор
),();,(
0000
yx
y
f
yx
x
f
∂
∂
∂
∂
e
r
(обозначаемый
gradu), то выражение для производной в направлении вектора
, можно записать
в виде
),( gradue
e
u
r
r
=
∂
∂
или
()
graduegradu
e
u
,cos
r
r
⋅=
∂
∂
Меняя направление вектора
e
r
, мы будем получать различные значения
e
u
r
∂
∂
.
В частности:
1)
0=
e
u
r
∂
∂
, если e ⊥gradu ((
r
e
r
,gradu) = 0).
2)
gradu
e
u
=
r
∂
∂
, если
gradu
gradu
=
r
e
, и это значение является наибольшим из возможных
((
e ,gradu) принимает наибольшее значение).
r
3)
gradu
e
u
−=
r
∂
∂
, если
gradu
gradu
−=
r
e
((e
r
,gradu) принимает наименьшее значение).
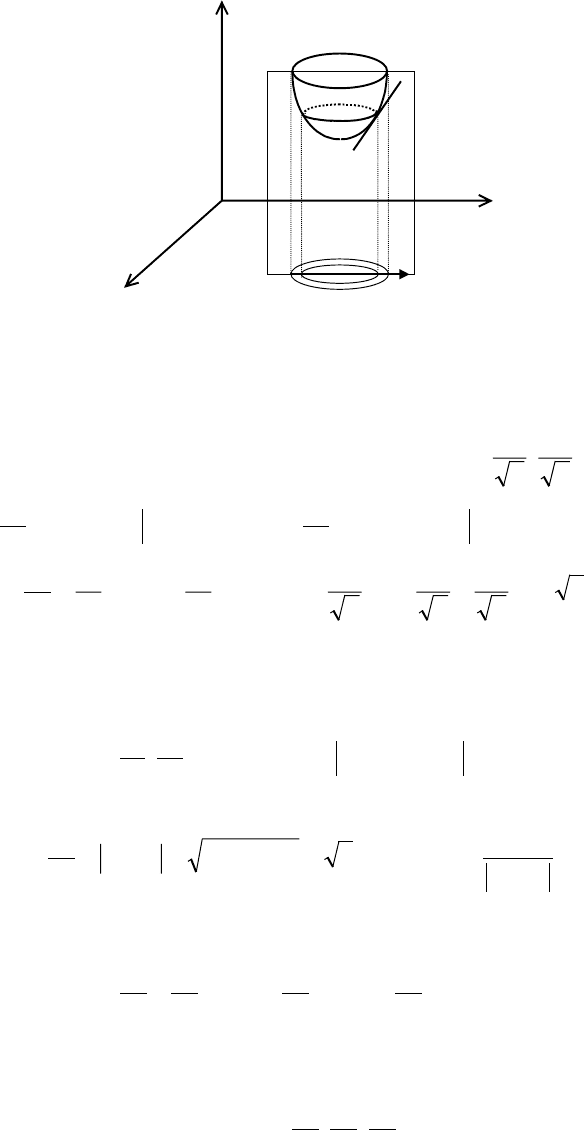
Таким образом, gradu определяет направление, в котором скорость
возрастания функции является наибольшей.
u
u=f(x,y)
gradu
x
y
Пример 1. Найти производную функции z = x
2
y
3
в точке (1,2) в направлении
вектора, составляющего с положительным направлением оси Ох угол 45
0
.
Координаты вектора
e имеют вид
r
{}
==
2
1
;
2
1
sin;cos
αα
e
r
12433)2,1( ;16822)2,1(
)2,1(
22
)2,1(
3
=⋅=⋅==⋅== yx
y
z
xy
x
z
∂
∂
∂
∂
219
2
38
2
1
12
2
1
16sincos ==⋅+⋅=⋅+⋅=
α
∂
∂
α
∂
∂
∂
∂
y
z
x
z
e
z
r
Пример 2. Найти grad(x
2
- y) в точке (1,1) и вычислить производную функции в
направлении градиента в этой точке
{}{}
1;21;2)( ;;
)1,1()1,1(
2
−=−=−
= xyxgrad
y
z
x
z
gradz
∂
∂
∂
∂
.
Производная функции в направлении градиента равна модулю градиента.
5)1(2
22
=−+== gradz
e
z
r
∂
∂
; где
gradu
gradu
e =
r
.
В трехмерном случае
γ
∂
∂
β
∂
∂
α
∂
∂
∂
∂
coscoscos ⋅+⋅+⋅=
z
f
y
f
x
f
e
f
r
,
r
где cos
α, cosβ, cosγ - направляющие косинусы вектора e .
Соответственно,
.;;
=
z
f
y
f
x
f
gradu
∂
∂
∂
∂
∂
∂
9.7. Частные производные и дифференциалы высших порядков функций
нескольких переменных
9.7.1. Частные производные высших порядков
