Никишкин В.А., Малахов А.Н., Максюков Н.И. Высшая математика
Подождите немного. Документ загружается.

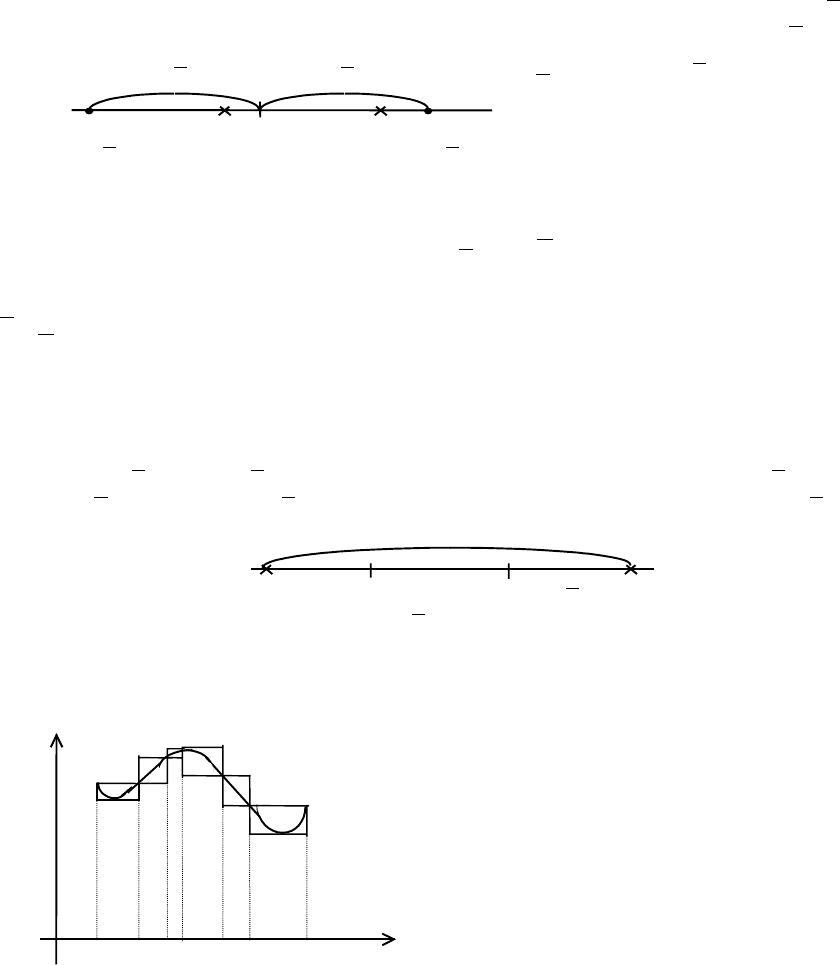
Теорема (о необходимом и достаточном условии квадрируемости плоской
фигуры). Для того, чтобы плоская фигура Q была квадрируемой, необходимо и
достаточно, чтобы для любого положительного числа
ε можно было указать такой
описанный вокруг фигуры Q многоугольник и такой вписанный в фигуру Q
многоугольник, разность S
d
-S
i
площадей которых была бы меньше ε, S
d
-S
i
<ε
Доказательство. Необходимость. Пусть фигура Q квадрируема, т.е. P =P =Р.
ε
2
ε
2
P −
ε
2
S
i
P S
d
P +
ε
2
Так как
{}
i
SsupP = и
{
}
d
SinfP = , то для любого
ε>0 можно указать такой
вписанный в фигуру Q
многоугольник, площадь
S
i
которого удовлетворяет неравенству
2
SP
i
ε
<− (3) и такой описанный около
фигуры Q многоугольник, площадь S
d
которого удовлетворяет неравенству
2
PS
d
ε
<− (4).
Складывая неравенства (3) и (4) получим S
d
-S
i
<ε.
Достаточность. Пусть S
d
и S
i
площади многоугольников, для которых S
d
-S
i
<ε и
так как S
i
≤P ≤P ≤ S
d
, то P -P <ε. Так как ε - произвольное число, то P =P и фигура
квадрируема.
S
i
{}
sup S P
i
=
{}
inf S P
d
=
S
d
Теорема доказана.
Площадь криволинейной трапеции.
y
a=x
0
x
1
x
2
x
n
=b x
Рассмотрим криволинейную
трапецию - фигуру, ограниченную
графиком непрерывной и
неотрицательной функции f(x),
заданной на сегменте [a,b],
ординатами, проведенными в
точках а и b и отрезком оси Ох
между точками а и b. Докажем
теорему.
Теорема. Криволинейная трапеция представляет собой квадрируемую фигуру,
площадь Р которой может быть вычислена по формуле
∫
=
b
a
dx)x(fP
Доказательство. Так как функция f(x)∈C[a,b], то эта функция интегрируема на
этом сегменте, поэтому
()
(
)
[
]
ε
ε
<
−
∃
>∀ sS:T0 , где S и s - верхняя и нижняя суммы
разбиения Т соответственно.
S=S
d
и s=S
i
, где S
d
и S
i
- площади ступенчатых многоугольников, причем
многоугольник площади S
d
содержит криволинейную трапецию, а площади S
i
-
содержится в ней. Поскольку S
d
-S
i
<ε, то из теоремы о необходимом и
достаточном условии квадрируемости плоской фигуры вытекает, что
криволинейная трапеция квадрируема. Поскольку
∫
==
→∆→∆
b
a
00
dx)x(fslimSlim
и Sps
≤
≤
, то
p
.
∫
=
b
a
dx)x(f
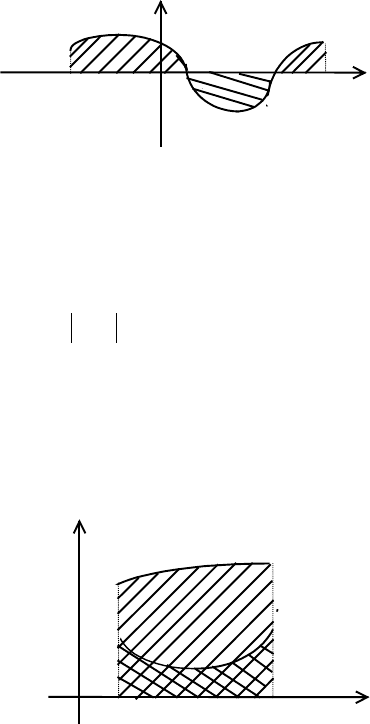
Замечание 1. Если функция f(x) непрерывна и знакопеременна на сегменте
y
+ +
a c — d b x
[a,b], то определенный интеграл
будет давать алгебраическую
сумму площадей, заключенных
между осью Ох, графиком функции
f(x) и
∫
b
a
dx)x(f
ординатами x=a, x=b. При этом площади над осью Ох будут получаться с
положительным знаком, а под осью Ох с отрицательным.
Для того, чтобы получить сумму этих площадей в обычном смысле, нужно
вычислить
∫
b
a
dx)x(f
. Так, сумма заштрихованных на рисунке площадей равна
∫∫∫
+−
b
d
d
c
c
a
dx)x(fdx)x(fdx)x(f
Замечание 2. Площадь, заключенная между двумя кривыми:
y
y
2
=f
2
(x)
y
1
=f
1
(x)
a b x
y
1
=f
1
(x), y
2
=f
2
(x) и двумя
ординатами: х=а, х=b в том
случае, когда одна кривая
лежит над другой, т.е.
f
2
(x)≥f
1
(x) на сегменте [a,b]
выражается интегралом.
[]
∫
−=
b
a
12
dx)x(f)x(fP
Если обе кривые лежат над осью Ох, то из чертежа видно, что
[]
∫∫∫
−=−=
b
a
12
b
a
1
b
a
2
dx)x(f)x(fdx)x(fdx)x(fP
В общем случае, если кривые как угодно расположены относительно оси
Ох, можно прийти к разобранному, если передвинуть ось Ох насколько вниз,
чтобы обе кривые оказались над осью Ох. В этом случае к обеим функциям f
2
(x) и
f
1
(x) прибавляется одно и то же постоянное слагаемое, причем разность f
2
(x)-f
1
(x)
остается без изменения.
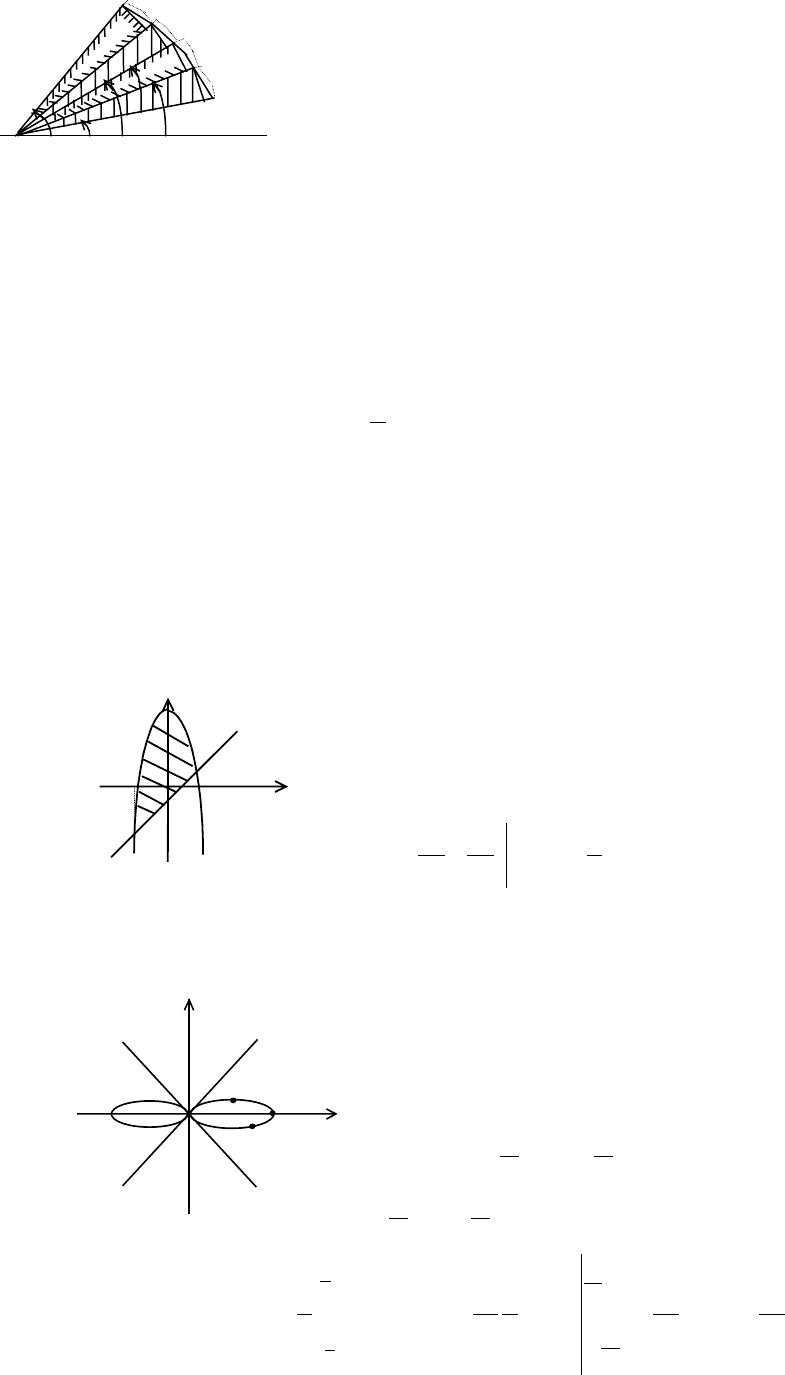
Площадь плоской фигуры в полярных координатах.
∆
Q
i
β
Q
i
Q
i-1
α
Пусть кривая L задана в полярной системе
координат уравнением r=r(
θ),θ∈[α,β]. Будем
считать, что r(
θ) непрерывна и
неотрицательна на сегменте [
α,β].
Криволинейным сектором называется
плоская фигура, ограниченная кривой L и
двумя лучами, составляющими с полярной
осью углы
α и β. Сформулируем без
доказательства следующую теорему.
Теорема. Криволинейный сектор представляет собой квадрируемую фигуру,
площадь которой может быть вычислена по формуле
∫
=
β
α
θθ
d)(r
2
1
P
2
Примеры.
1. Найти площадь фигуры, заключенной между кривыми y=5-x
2
и
y=x-1. Решая совместно уравнения
, получим
−=
−=
1xy
x5y
2
5
-3 2 x
.
1y
2x
;
4y
3x
2
2
1
1
=
=
−=
−=
Следовательно,
()
()
[]
()
6
5
20
3
2
3
x
2
x
x6
dxxx6dx1xx5P
32
2
3
2
2
3
2
=
−
−−=
=−−=−−−=
∫∫
−−
2. Найти площадь фигуры, ограниченной одним лепестком кривой
(лемниската).
ϕρ
2cosa
22
=
A
B
0 C
Правая часть уравнения данной
кривой неотрицательна при тех
значениях
ϕ, для которых cos2ϕ≥0,
поэтому первый лепесток лежит в
угле, где
2
2
2
π
ϕ
π
≤≤− , т.е.
44
π
ϕ
π
≤≤− .
Следовательно,
=
−
==
∫
−
4
4
2sin
2
1
2
a
d2cosa
2
1
P
2
4
4
2
OABC
π
π
ϕϕϕ
π
π
2
a
)11(
4
a
22
=+
7.12. Объем тела вращения
Вычисление объема тела сводится также к вычислению определенного интеграла.
Пусть рассматриваемое тело Е получается от вращения данной кривой y=f(x),
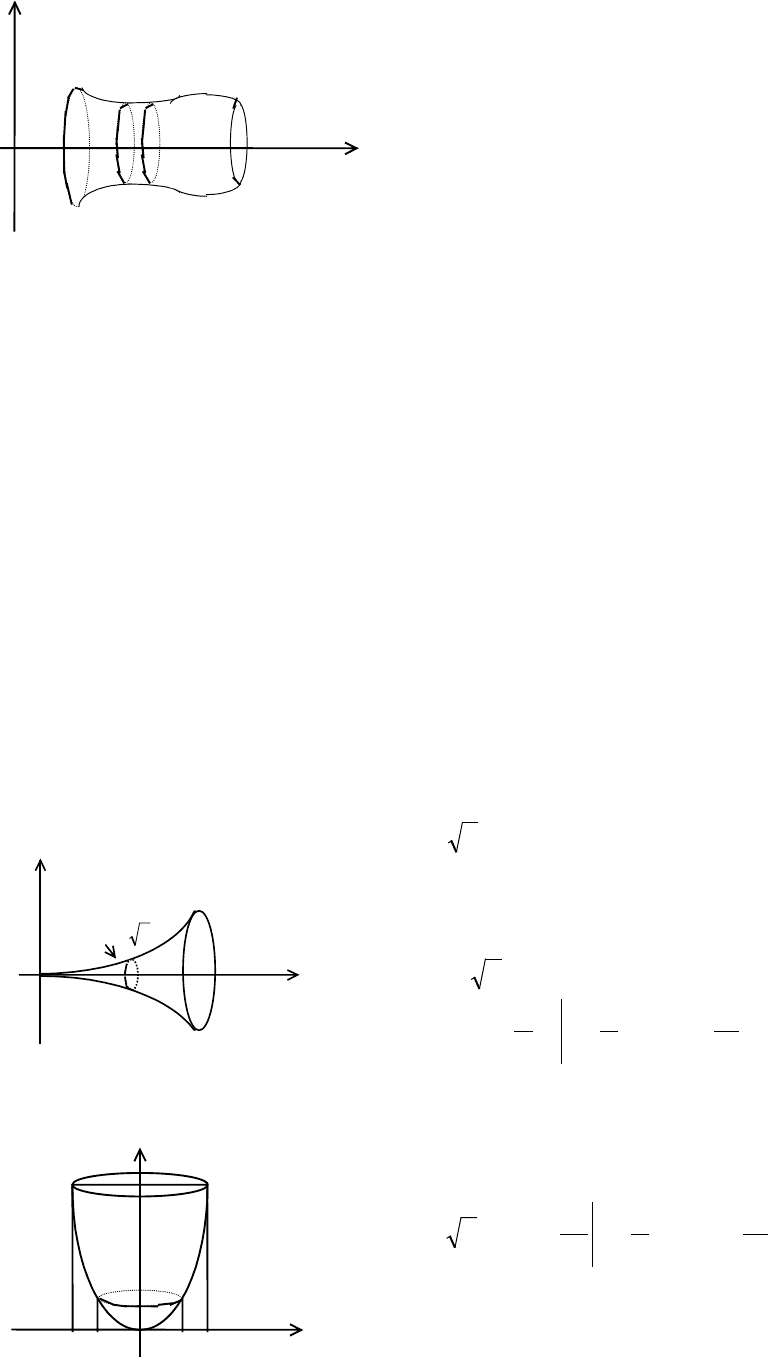
заданной на сегменте [a,b], вокруг оси Ох. Обозначим через V объем данного
тела. Разобьем тело поперечными сечениями, перпендикулярными к оси Ох,
начиная от х=а и кончая х=b.
y
∆
E
a b
x
0
x
0
+
∆
x x
Очевидно поперечные сечения -
круги радиуса у. Рассмотрим один
из элементов
∆Е, образованный
сечениями с абсциссами х и х+
∆х.
Будем считать, что
∆х достаточно
мало и заменим объем тела
∆Е
объемом прямого цилиндра, высота
которого
∆х, а площадь ос-
нованияS(x)=
Πf
2
(x) и, следовательно, для объема V тела получим приближенное
выражение
(суммирование берется по всем элементам, на которые
наше тело разбито поперечными сечениями). При переходе к пределу, когда
число элементов беспредельно возрастает и наибольшее из
∆х→0, написанная
сумма превращается в определенный интеграл, который дает точное значение
объема V,
∑
∆≈ x)x(SV
∫
=
b
a
2
dx)x(fV
π
.
Итак, приходим к следующей теореме.
Теорема. Объем тела, получаемого при вращении вокруг оси Ох кривой y=f(x),
заключенный между ординатами х=а и х=b, выражается формулой
∫∫
==
b
a
2
b
a
2
dx)x(fdxyV
ππ
Пример. Вычислить объем тела, образованного вращением вокруг осей Ох и Оу
фигуры, ограниченной ветвью параболы
yx = и отрезком 1≤у≤4 оси координат.
y
xy=
1 2 x
Рис.1
y
4
1
Рис.2
1. Вычислим объем V тела
образованного вращением параболы
вокруг оси Ох. (см. рис.1).
Так как
yx = , то y=x
2
π
ππ
π
5
31
)132(
5
1
2
x
5
dxxV
5
2
1
4
=−==
∫
2. Если V
1
- объем тела, образованного
вращением параболы вокруг оси Оу
(см. рис.2)
()
π
π
ππ
2
15
)116(
2
1
4
2
y
dyyV
2
4
1
2
1
=−===
∫
8. Обобщение понятия определенного интеграла. Несобственные интегралы
Введенное ранее понятие определенного интеграла не пригодно для
неограниченной функции и для случая, когда подынтегральная функция не
ограничена. Рассмотрим некоторые возможные обобщения понятия
определенного интеграла.
8.1. Несобственные интегралы с бесконечными пределами интегрирования
Будем предполагать, что функция f(x) непрерывна на полупрямой
∞
+
≤
x
a , тогда
она непрерывна на любом отрезке [a,b], где b>a и, следовательно, существует
интеграл
∫
b
a
f(x)dx
.
Этот интеграл является функцией своего верхнего предела в
,
определенной на промежутке
∫
=
b
a
f(x)dxbF )(
+
∞
<
≤
ba . Если при
+
∞→b
∫
+∞
a
F(b) стремится к
конечному пределу, то этот предел обозначают
и называют
несобственным интегралом по бесконечному промежутку (от а до бесконечности)
от функции f(x). Таким образом, по определению
f(x)dx
∫∫
+∞→
+∞
=
b
a
b
a
dxxff(x)dx )(lim
,
если этот предел существует и конечен. В этом случае принято говорить, что
несобственный интеграл
существует или сходится.
∫
+∞
a
f(x)dx
В противном случае: если предел не существует или предел бесконечен, то
символу
никакого словесного числового смысла не приписывают и,
называя его снова несобственным интегралом, говорят, что этот несобственный
интеграл существует или расходится.
∫
∞
a
f(x)dx
Аналогичным образом для функции f(x), непрерывной на полупрямой
bx
≤
<
∞
−
,
определяется несобственный интеграл .
∫
∞−
b
f(x)dx
При этом
, если этот предел существует и конечен.
∫∫
−∞→
∞−
=
b
a
a
b
dxxff(x)dx )(lim
Для функции f(x), непрерывной на всей числовой оси, несобственный интеграл
определяется равенством:
∫∫∫
+∞
∞−
+∞
∞−
+=
c
c
dxxfdxxff(x)dx )()(
,
где с – любое число, а каждый из интегралов в правой части равенства сходится.
При этом несобственный интеграл
называется сходящимся. (Его
∫
+∞
∞−
f(x)dx
величина, очевидно, не зависит от числа с). Если хотя бы один из интегралов
и расходится, то несобственный интеграл
называется расходящимся.
∫
∞+
c
f(x)dx
∫
+∞
c
f(x)dx
∫
f(x)dx
∫
+∞
∞−
f(x)dx
0
-Y
lim
1
2
x
dx
b
=
+
∞
→
=
+
∞
→
∫
lim
1
0
2
x
xdx
b
Из сделанных выше определений сходящихся несобственных интегралов с
бесконечными пределами интегрирования следует, что эти интегралы являются не
пределами интегральных сумм, а пределами определенных интегралов с
переменными верхними или нижними пределами при стремлении этих пределов к
бесконечности.
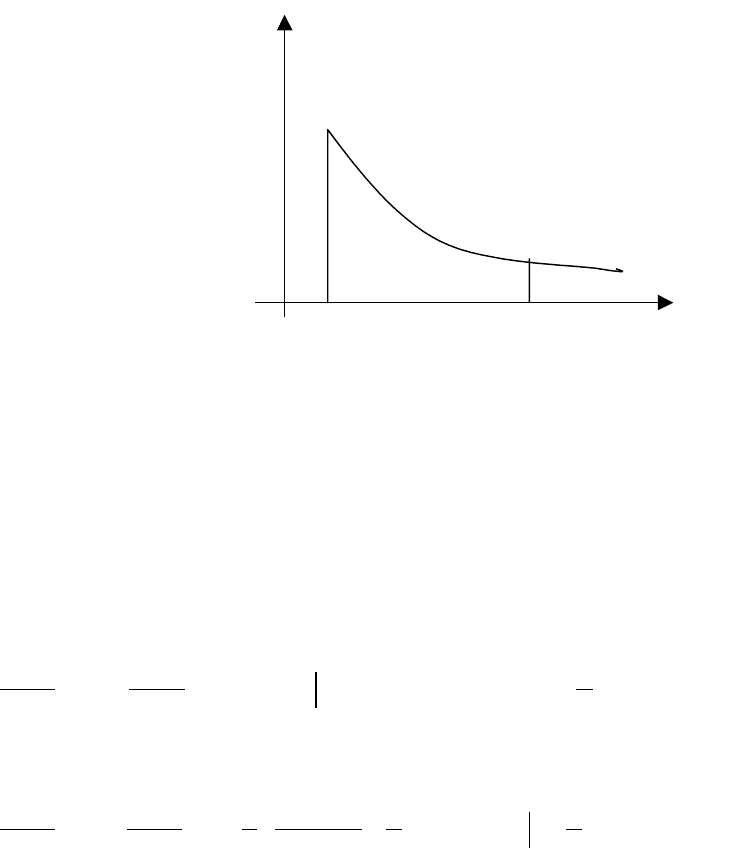
Если функция f(x) непрерывна и неотрицательна на бесконечном промежутке
[a,+
∞), то численно равен площади криволинейной трапеции,
ограниченной снизу отрезком [a,b] оси OX, сверху кривой y=f(x), слева и справа -
прямыми x=a и x=b. При возрастании b прямая x=b, ограничивающая эту
криволинейную трапецию, движется направо.
b
a
В случае, если при этом несобственный интеграл
сходится, его
величину естественно принять за площадь бесконечной полосы, ограниченной
снизу осью ОХ, сверху – графиком функции y=f(x), слева – прямой х=а (рис.).
∫
+∞
a
f(x)dx
а
b
X
y=f(x)
Аналогичные рассуждения имеют место и для интегралов вида:
∫
∞−
b
f(x)dx
и .
∫
+∞
∞−
f(x)dx
Несобственные интегралы с бесконечными пределами иногда называют
несобственными интегралами первого рода.
Рассмотрим несколько примеров несобственных интегралов первого рода:
Пример 1.
()
2
0limlim
1
00
0
2
π
arctgarctgb
arctgx
x
dx
b
b
b
b
=−==
+
+∞→∞→=∞
∫∫
.
Пример 2.
∞=−+=+=
+
+
=
+
∞→∞→∞→∞
∫∫
)1ln)1(ln(
lim
2
1
)1(ln
lim
2
1
1
)1(
2
1
lim
1
2
0
2
2
2
0
2
bx
x
xd
x
xdx
b
b
bb
b
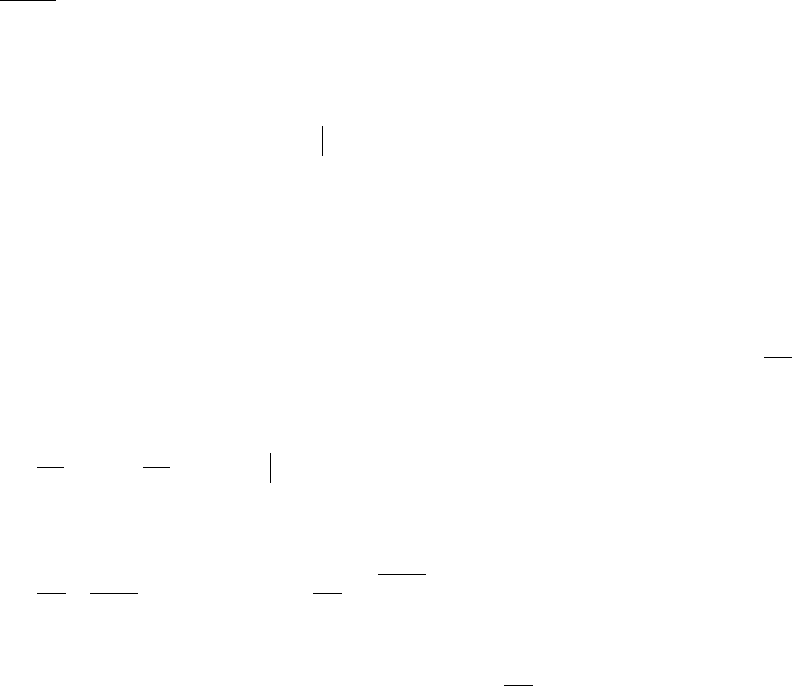
∫
∞
+
0
2
1 x
xdx
- расходится.
Пример 3.
)0sin(sin
lim
sin
lim
cos
lim
cos
0
00
−===
∞→∞→∞→
+∞
∫∫
bxxdxxdx
b
b
b
b
b
∫
∞
0
cos xdx
- этот предел не существует, значит
- расходится.
Пример 4.
Исследуем на сходимость интеграл, зависящий от параметра р:
∫
∞
1
p
x
dx
.
1. Если , то имеем: 1=p
()
∞=−===
+∞→+∞→
∞
+∞→
∫∫
1lnlnlimlnlimlim
1
11
bx
x
dx
x
dx
b
b
b
b
b
- интеграл расходится.
2. Если , то для любого b>0 имеем: 1≠p
()
1
1
1
1
1
−
−
=
−
∫
p
b
p
b
px
dx
и
<∞
>
−
=
∫
+∞→
1ð åñëè ,
1ð åñëè,
1
1
lim
1
p
x
dx
b
p
b
Таким образом, несобственный интеграл
∫
∞
1
p
x
dx
сходится при р>1 и расходится при
. 1≤p
Некоторые свойства несобственных интегралов
Приведем без доказательства свойства несобственных интегралов первого рода.
1. Пусть f(x) – непрерывна на полупрямой
[
)
+
∞,a , тогда интегралы и
а
∫
+∞
a
dxxf )(
∫
+∞
1
)(
a
dxxf
1
>a, ведут себя одинаково относительно сходимости.
2. Если
сходится и равен S, то интеграл , где с – произвольное
число, также сходится и равен
∫
+∞
a
dxxf )(
∫
+∞
a
dxxcf )(
Sc
×
.
3. Если интегралы
и сходится и соответственно равны S
∫
+∞
a
dxxf )(
1
− xfx ()(
21
∫
+∞
a
dxxf )(
2
dx
1
и S
2
,
то интеграл
также сходится и равен S
∫
+∞
a
f ))(
1
+S
2
.
Критерий Коши
Для сходимости интеграла необходимо и достаточно, чтобы для любого
ε>0 можно указать А=А(ε), такое, что для любых R' и R'', больших А, выполняется
неравенство:
∫
+∞
a
dxxf )(
ε
<
∫
``
`
)(
R
R
dxxf
Необходимое условие сходимости несобственных интегралов
Если интеграл
сходится, то его частные интегралы ограничены, то есть
существует такое число М>0, что для всех b>a выполняется неравенство
∫
+∞
a
dxxf )(
Mdxxf
b
a
<
∫
)(
Это утверждение непосредственно вытекает из существования конечного предела
частных интегралов при
b . ∞→
Таким образом, если частные интегралы не ограничены, то несобственный
интеграл расходится. Если же частные интегралы ограничены, то о сходимости
несобственного интеграла еще ничего сказать нельзя: в одних случаях интеграл
может сходиться, а в других – расходиться.
Например, у несобственного интеграла
частные интегралы
∫
+∞
0
cos xdx
bxxdx
b
b
sinsincos
0
0
==
∫
+∞→b
∫
+∞
0
cos xdx
ограничены, но они не имеют предела при (так как sin
b при
не имеет предела) и, следовательно, несобственный интеграл
- расходится.
+∞→b
Несобственные интегралы от неотрицательных функций
Если подынтегральная функция f(x) на полупрямой
[
)
+∞,a непрерывна и
неотрицательна, то ограниченность частных интегралов является необходимым и
достаточным условием сходимости интеграла
.
∫
+∞
a
dxxf )(
Признак сравнения несобственных интегралов
Если функции f(x) и g(x) непрерывны на полупрямой
[
)
+
∞,a и удовлетворяют на
нем условию
)()(0 xgxf
≤
≤ , то из сходимости интеграла
∫
+∞
a
dxxg )(
(1)
следует сходимость интеграла
∫
+∞
a
dxxf )(
(2),

и обратно: из расходимости интеграла (2) следует расходимость интеграла (1).
Следствие:
Если f(x) и g(x) – непрерывные функции на полупрямой
[
)
+
∞,a и R
xg
xf
x
=
+∞→
)(
)(
lim
)( dxxg
(где
R – действительное число: 0<R<
∞), то интегралы и сходятся
или расходятся одновременно.
∫
+∞
0
(xf )dx
∫
+∞
0
Абсолютная и условная сходимость несобственных интегралов
Определение. Пусть f(x) – произвольная непрерывная на полупрямой
[
)
+
∞,a
функция, необязательно знакопостоянная. Интеграл
называется
абсолютной сходящимся, если сходится интеграл
∫
+∞
a
dxxf )(
∫
+∞
a
dxxf )(
.
Теорема. Если сходится интеграл
∫
+∞
a
dxxf )(
, то сходится и интеграл .
∫
+∞
a
dxxf )(
Отметим, что сходимость несобственного интеграла от знакопеременной функции
не влечет за собой его абсолютной сходимости, а для интегралов от
знакопостоянных функций их сходимоти интеграла следует его абсолютная
сходимость.
Например, интеграл
dx
x
x
a
∫
+∞
sin
(a>0) сходится, а интеграл
dx
x
x
a
∫
+∞
sin
расходится, то
есть интеграл
dx
x
x
a
∫
+∞
sin
не является абсолютно сходящимся. (Такие интегралы
называют условно сходящимися).
Интеграл
dx
x
x
a
∫
+∞
2
sin
(a>0) сходится абсолютно, так как
22
1sin
xx
x
≤ , и интеграл
∫
+∞
a
x
dx
сходится.
8.2. Несобственные интегралы от неограниченных функций
Пусть теперь функция f(x) задана на полуинтервале [a,b). Точку b будем называть
особой, если функция f(x) не ограничена на [a,b), но ограничена на любом [a;b-
α]⊂[a,b). Будем также предполагать, что на любом таком сегменте функция f(x)
интегрируема.
В наших предположениях на [a;b-
α] задана функция аргумента α .
∫
−
=
α
α
b
a
dxxfF )()(
Исследуем вопрос о правом предельном значении функции F(x) в точке α=0, то
есть вопрос о существовании предела:
∫
−
+→
α
α
b
a
dxxf )(lim
0
.

При этом для обозначения этого выражения будем использовать обозначение:
. В дальнейшем этот символ будем называть несобственным интегралом
второго рода от функции f(x) по полуинтервалу [a;b). Если указанный предел
существует, интервал будем называть сходящимся, если предел не существует
или равен
∞, то интеграл будем называть расходящимся.
∫
b
a
f(x)dx
Аналогично для функции f(x), непрерывной на полуинтервале (a;b) и
неограниченной вблизи а, вводится понятие несобственного интеграла
.
∫
b
a
f(x)dx
Полагают, что
, если этот предел существует и конечен.
∫∫
+
+→
=
b
a
b
a
dxxff(x)dx
α
α
)(lim
0
Несобственный интеграл от функции f(x), непрерывной на интервале (a;b) и
неограниченной вблизи его концов а и b, определяется равенством:
∫∫∫
+=
b
ñ
ñ
a
b
a
f(x)dxf(x)dxf(x)dx
,
где с – любая точка интервала (a;b), если каждый из несобственных интегралов
и сходится. При этом несобственный называется
сходящимся, его величина не зависит от выбора числа с. если хотя бы один из
интегралов
и расходится, то несобственный интеграл
называют расходящимся.
∫
ñ
a
f(x)dx
∫
b
ñ
f(x)dx
∫
ñ
a
f(x)dx
∫
b
a
f(x)dx
∫
b
ñ
f(x)dx
∫
b
a
f(x)dx
Пусть теперь функция f(x) непрерывна на отрезке [a;b] всюду, кроме
некоторой точки с, a<c<b, и не ограничена вблизи с.
Несобственный интеграл
определяется равенством
, если каждый из интегралов в правой части равенства
сходится. Если хотя бы один из этих интегралов расходится, то несобственный
интеграл
называется расходящимся.
∫
b
a
f(x)dx
∫∫∫
+=
b
ñ
ñ
a
b
a
f(x)dxf(x)dxf(x)dx
∫
b
a
f(x)dx
Аналогично определяется несобственный интеграл по отрезку [a;b] от
функции, непрерывной на нем всюду, кроме конечного числа точек, и
неограниченной вблизи этих точек.
Рассмотрим несколько примеров несобственных интегралов второго рода.
Пример 1.
∫
1
0
p
x
dx
, где р>0.
Это несобственный интеграл второго рода, так как
p
x
y
1
=
, где р>0, –
неограниченная на (0;1) функция:
+∞=
+→
p
x
x
1
lim
0
.
