Останкова Л.А., Шевченко Н.Ю. Аналіз, моделювання та управління економічними ризиками

Подождите немного. Документ загружается.

Аналіз, моделювання та управління економічними ризиками

Чисельні оцінки

Задача полягає у співвідношенні системі оцінки одного числа.

Для її вирішення використовується експертиза Е1:

ȍ = E

;

= E

;

L — експерти ізольовані;

Q — зворотний зв’язок відсутній;

∑

)...,,(

(79)

Результуюча оцінка знаходиться за формулою середньозва-

женого значення, де

),1( Ni

— вагові коефіцієнти експертів.

При відсутності інформації про компетентність експертів можна

вважати

),1( Ni =

. Ступенем погодженості думок експертів

в експертизі Е1 є дисперсія

∑

−

)(

, (80)

де

— оцінка i-го експерта;

a — результуюча оцінка.

Експертиза Е2, яка є модифікацією експертизи Е1 для підви-

щення точності оцінювання, характеризується параметрами:

= E

Останкова Л. А., Шевченко Н. Ю.

∑

Nii

NNN

xxx

xxxxxxxxx

321

332211

321

),,...,,,,,,,(

γγγ

(81)

Інші параметри ті ж, що й у експертизі Е1. Ступінь погодже-

ності методу оцінками визначається виразом

∑

−

)(

σα

, (82)

де Į

— середня оцінка i-го експерта,

413

/)(

γσ

aa −=

;

— ступінь невпевненості експерта у власній відповіді.

В експертизі Е2

iii

aaa

321

інтерпретуються як оптимістична,

найбільш ймовірна та песимістична оцінки i-го експерта відпо-

відно. Коефіцієнти

визначаються емпірично. За однією

методикою Ȗ

= 1, Ȗ

= 4, Ȗ

= 1, Ȗ

= 36, за іншою Ȗ

= 3, Ȗ

= 0, Ȗ

= 2,

= 25 (за другою методикою

γγ

, оскільки там вважається, що

особа схильна занижувати оцінки).

В експертизах Е1 та Е2 можна визначити статистичну значу-

щість отриманих результатів. Маючи ймовірність помилки

пом

вказується інтервал, в який величина оцінки потрапляє із ймо-

вірністю 1 – P

пом

Δ+≤≤Δ− aaa

; (83)

вважається, що величина a розподілена нормально з центром

та дисперсією (82). Тоді

Nt /

=Δ

, де величина t має розподіл

Стьюдента з

1−N

ступенів вільності. Її визначають за таблицями

Стьюдента, маючи величину P

пом

Приклад 1. Десять експертів з однаковими ваговими коефіцієн-

тами

)10,1(1 i

оцінюють величину T. Від них отримані наступні

оцінки:

Аналіз, моделювання та управління економічними ризиками

1234 5678910

20, 24, 22, 37,T 40, 35, 28, 31, 21, 25,5TTTT TTTTT==========

Значення

(за формулою 79) дорівнює 28,35. Дисперсія

(за формулою 80) дорівнює 45,3; ı = 6,73.

Маючи ймовірність помилки P

пом

= 0,05, за таблицями роз-

поділу Стьюдента визначаємо величину

t: ступенів вільності 9;

262,2=t

8,4=Δ

. Таким чином, оцінювана величина з ймовірністю

0,95 знаходиться в інтервалі [23,5; 33,2].

Використання методу Дельфі для чисельної оцінки у вигляді

експертизи Е3 має вигляд:

ȍ = E

;

⎭

⎬

⎫

⎩

⎨

⎧

≥=∈=Ω

∑

0,1

iike

zzkEz

; (84)

L — експерти ізольовані;

Q — експертам надана медіана q

(86), діапазон квантилів (87)

та обґрунтування оцінок, які виходять за даний діапазон.

Відображення ĳ задається наступним чином: увесь інтервал

припустимих значень величини, яка оцінюється, ділиться на

інтервалів

tt ...,,

; експерт оцінює ймовірність знаходження ве-

личини, яка оцінюється, в кожному з інтервалів; за результатами

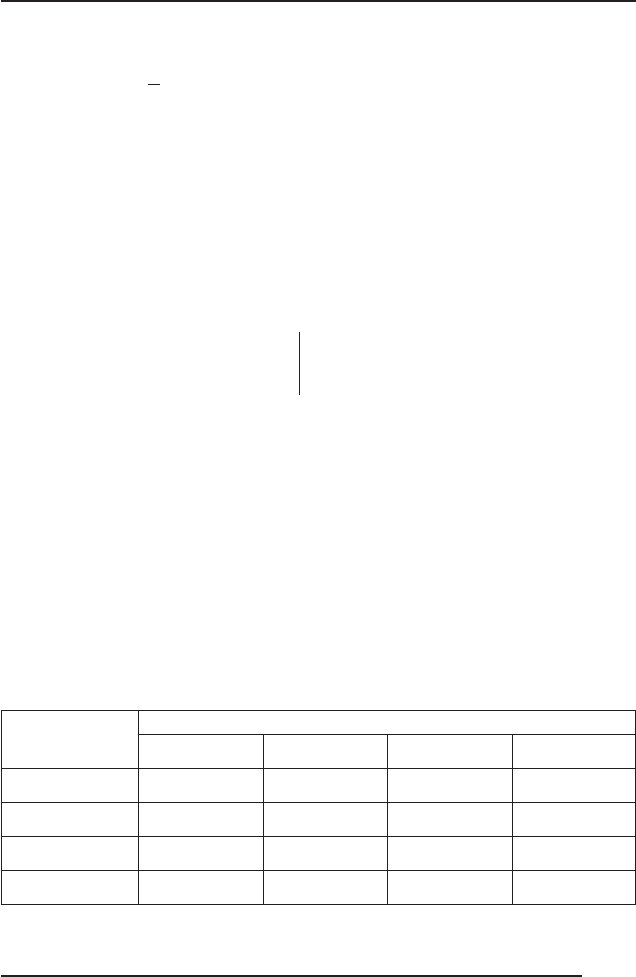
їх оцінок складається табл. 6, де p

— оцінка ймовірності знахо-

дження величини, яка оцінюється в j-му інтервалі, що надана i-м

експертом.

Таблиця 6

Експерти

Інтервали

12…

…

… …………

…

Останкова Л. А., Шевченко Н. Ю.

На основі даної таблиці визначається думка експертів про зна-

ходження величини, яка оцінюється, у кожному з інтервалів

t :

∑

iij

()

kj ,1= (85)

Результуючою оцінкою

))(...,),((

1 eNe

CC ΩΩ

є медіана отри-

маного розподілу

, що визначається з умови:

5,0)(

=≤ qTP

. (86)

Крім

розраховується діапазон квантилів:

qqq −=Δ

, (87)

де P(T  q

) = 0,75; P(T  q

) = 0,25. Емпірично встановлено, що

процедуру можна припиняти, якщо діапазон квантилів зменшу-

ється у 1,6 раза порівняно з попереднім.

Ранжирування

Жорстке ранжирування полягає у тому, щоб поставити у від-

повідність системі одну перестановку. Визначимо експертизу Е4:

Ω — множина всіх перестановок;

Ω=Ω

;

L — експерти ізольовані;

Q — зворотний зв’язок відсутній.

Відображення ĳ задається наступним чином: результати опи-

тування експертів зводяться у табл. 7.

Аналіз, моделювання та управління економічними ризиками

Таблиця 7

Експерти

Об’єкти

12…

…

… …………

…

∑

рангів

…

i-му рядку стоять ранги, надані i-м експертом об’єктам ран-

жирування. У (N +1)-му рядку знаходяться суми рангів за всіма

експертами для певного об’єкта. Всі n об’єктів упорядковані від-

повідно до величини r

, яка визначається за формулою

sjs

. (88)

На перше місце ставиться об’єкт, у якого r

мінімальне, і так

далі.

Ступінь узгодженості думок експертів визначається за допо-

могою коефіцієнта конкордації

Розглянемо два випадки: а) ранжирування всіх експертів спів-

падають, якщо кожний об’єкт отримав від усіх експертів однаковий

ранг, який для

j-го об’єкта складає r

/N; б) повна неузгодженість

думок експертів, тобто протилежність оцінок ранжирування, які

надаються експертами. Виходячи із (88) маємо:

∑∑∑∑∑

=== ==

⎟

⎠

⎞

⎜

⎝

⎛

ijiji

rrr

111 11

(89)

Сума рангів, які надаються кожним експертом (тобто вираз

в дужках у (89)), завжди дорівнює

2/)1( +nn

. Тому



nNnr

2/)1(

Останкова Л. А., Шевченко Н. Ю.

За середній ранг приймають величину



isri

nNnrr

2/)1(/

, (90)

а за ступінь узгодженості думок — суму квадратів відхилень

від середнього значення r

Коефіцієнтом конкордації

для випадку жорсткого ранжи-

рування, тобто відсутності рівних рангів при ранжируванні кож-

ного експерта, називається величина

)nn(N

)1n(N

r12





, (91)

де

n — кількість об’єктів, N — кількість експертів.

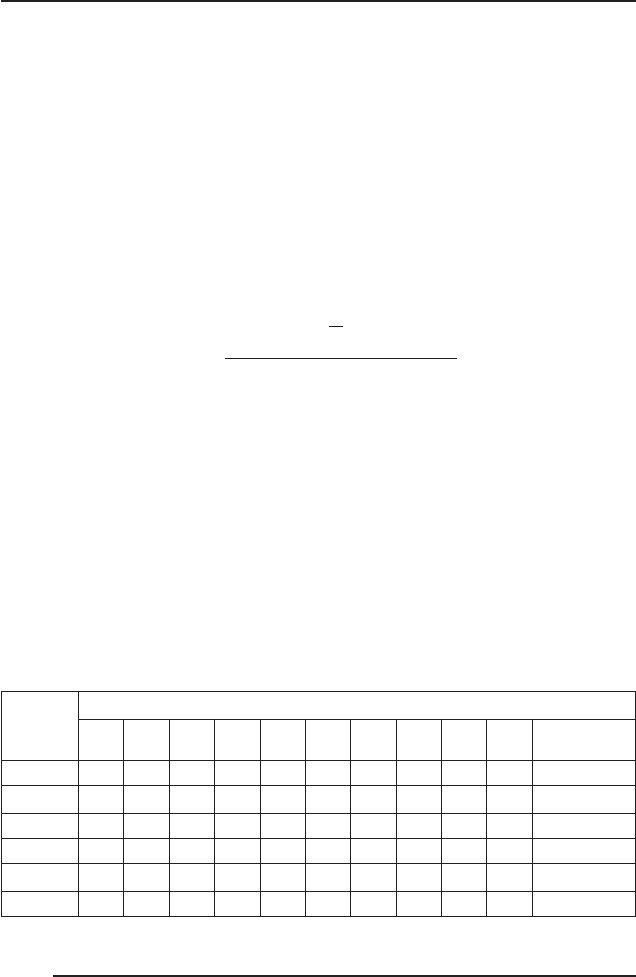
Приклад 2. Нехай проводиться експертиза оцінки технологіч-

ного процесу. Існує перелік із шести ознак, які впливають на про-

цес, десять експертів здійснювали ранжирування цих ознак за важ-

ливістю. Результати їх нової роботи наведені у табл. 8. Розрахуємо

коефіцієнт конкордації. Суми рангів відповідно до (88) дорівню-

ють:

= 52, r

= 46, r

= 19, r

= 27, r

= 21, r

= 45. Із (90) знаходимо

i sr

= 35. Підставляючи знайдені величини у (91), отримаємо W =

0,690

Таблиця 8

Озна-

ки

Номер експерта

12345678910

1 6466566616 52

2 3554655454 46

3 2121133222 19

4 4233322341 27

5 1315211133 21

6 5642444565 45

Аналіз, моделювання та управління економічними ризиками

Нежорстке ранжирування полягає у тому, щоб поставити

у відповідність системі нежорстке ранжирування (вектор з певними

властивостями). При цьому деякі об’єкти можуть бути рівноцінни-

ми. Їм приписуються однакові ранги. Так, якщо об’єкти поділяють

місця 4–5, то кожний із них отримує ранг 4,5.

Експертиза Е5 для нежорсткого ранжирування відрізняється

від експертизи Е4 тільки множиною

Ω .

Коефіцієнт конкордації для нежорсткого ранжирування ви-

значається формулою:

¦¦





)tt(N)nn(N

)1n(N

r12

, (92)

де

— кількість груп рівних рангів, введених i-м експертом;

— кількість дрібних рангів в j-й групі, введених i-м експер-

том.

Статистичну значущість ранжирування перевіряють, обира-

ючи імовірність помилки P

пом

. Вважають, що величина

WnN )1( −

має

-розподіл з (n – 1) ступенем вільності. За P

пом

за спеціальними

таблицями знаходять табличне значення W

. Якщо коефіцієнт W,

отриманий при реалізації експертизи, більший чи дорівнює W

то отримане ранжирування вважають статистично значущим.

Приклад 3. Визначимо статистичну значущість прикладу 2.

Нехай необхідно, щоб ймовірність помилки, тобто ймовірність того,

що отримане ранжирування є випадковим,

пом

= 0,01. Визна-

чимо величину N = (n – 1) W = 10 · 5 · 0,69 = 34,5. Із таблиць роз-

поділу

для числа ступеня вільності, що дорівнює 5, знаходимо

086,15)5(

01,0

, що відповідає табличному значенню величини N

= (n – 1) W

. Знайдене значення, яке дорівнює 34,5, більше таблич-

ного, тобто отримане ранжирування статистично значуще.

Вище малося на увазі, що експерти мають рівну компетент-

ність. Однак якщо компетентність експертів різна і може бути оці-

нена деяким числом, то формули (88)– (92) потребують уточнення.

Нехай компетентність

j-го експерта оцінюється додатною ве-

личиною

(вага експерта). Будемо вважати ці величини

Останкова Л. А., Шевченко Н. Ю.

нормованими

⎟

⎠

⎞

⎜

⎝

⎛

∑

. Суму рангів r

об’єктів будемо розрахову-

вати за формулою

∑

jiji

. Коефіцієнт конкордації з урахуван-

ням компетентності експертів визначається за формулою (92). Пе-

ревірку статистичної значущості здійснюють аналогічно

(перевіряють значущість погодженості думок експертів).

Метод парних порівнянь для нежорсткого ранжирування. Екс-

периментально встановлено, що великою складністю для експерта

є побудова ранжирування на основі одночасного обліку декількох

різних ознак, за якими оцінюються об’єкти. У цих випадках екс-

перти вирішують задачі попарного порівняння.

Визначимо експертизу Е6 для вирішення задачі нежорсткого

ранжирування:

ȍ — множина всіх перестанов;

— множина всіх матриць A = (a

де

)n,1ji(0a),ji(1aa,1,0a

z 

; (93)

L — експерти ізольовані;

Q — зворотний зв’язок відсутній.

Відображення

ĳ задається наступним чином: визначають

матрицю

AaA

)(

, де

)(

— оцінка j-го експерта.

Знаходять величини

iss

nsaa

),1(

. Об’єкти упорядковують

відповідно до величини a

. Об’єкти з мінімальним a

отримують ранг

1 і т. ін.

У методі парних порівнянь кожний з експертів здійснює

порівнянь, тобто порівнює кожний об’єкт один з одним. Результат

порівняння

j-го експерта представляється матрицею розміру

nn ×

, де 1=

a , коли на думку експерта i-му об’єкту надається

перевага у порівнянні з

k-м. Для будь-якої пари об’єктів

>< qp,

Аналіз, моделювання та управління економічними ризиками

надається перевага p у порівнянні з q, і навпаки. Це й відобража-

ється умовами (93)

за визначенням.

Матриця A

, подана j-м експертом

Nj ,1=

, є матрицею деяко-

го бінарного відношення, яке називається відношенням наданих

переваг експерта.

Коефіцієнтом сумісності думок експертів називається вели-

чина

124/( ),

124/( 4),

dn n

⎧

−−

⎪

⎨

−−

⎪

⎩

де d — кількість циклів довжини 3. Величину v можна викорис-

товувати в якості оцінки компетентності експерта при експертизах

типу Е6.

Рангова кореляція

Нехай

><><

jjii ...,,,...,,

— два нежорстких ранжируван-

ня. Припустимо, що



!



;,1

,,1

,,0

iiɹɤɳɨ

(95)

аналогічно визначимо величини d

для другого ранжирування.

Коефіцієнтом рангової кореляції Кендалла називається величина

2/)1(



¦¦

stst

. (96)

Розрахувавши коефіцієнт

Ĳ, оцінимо значущість зв’язку між

ранжируваннями. Для цього позначимо чисельник (96) через S.

Якщо зафіксувати одне ранжирування та розглядати всі n! інших

якщо n парне;

якщо n непарне;

(94)

Останкова Л. А., Шевченко Н. Ю.

жорстких ранжирувань, можна знайти частоту всіх можливих

значень

S. При n > 10 розподіл S наближається до нормального

із середньоквадратичним відхиленням

18/)52)(1(  nnn

. При

n  10 розподіл S можна знайти у спеціальних таблицях.

У загальному випадку, якщо величина S набуває значення S

чи

більш маловірогідне, то гіпотеза про незалежність ранжирування

відкидається. Якщо

{}

Pr ³SS p=<

, то отриманий коефіцієнт Ĳ

вважається значущим. Величину p

задають як рівень значущості;

порівнюють розраховане значення

S з табличним для даного рівня

значущості p

1.6.6. Побудова узагальненої оцінки

при обробці експертами інформації

Висувається гіпотеза H

про те, що експерти є досить точни-

ми вимірниками, на основі підтвердження якої можна виявити

можливі формулювання в експертній групі. Ступінь погодженості

експертних оцінок виражається за допомогою коефіцієнта пого-

дженості. Розглянемо алгоритми побудови узагальненої оцінки

при частковій модифікації експертиз Е1-Е6.

Постановка завдання

Маємо m об’єктів та d експертів, побудована матриця резуль-

татів ранжирування наявних об’єктів даними експертами з еле-

ментами r

, де r

— ранг, привласнений j-м експертом i-му об’єкту.

Необхідно визначити ступінь погодженості експертних оцінок.

Алгоритм рішення

1. Розраховується сума рангів за кожним рядком:

iji

, (97)