Останкова Л.А., Шевченко Н.Ю. Аналіз, моделювання та управління економічними ризиками

Подождите немного. Документ загружается.

Аналіз, моделювання та управління економічними ризиками

Повна невизначеність — такий вид невизначеності, що

характеризується близькою до нуля прогностичністю подій:

0lim =

→

, (1)

де

— імовірність настання події;

t — час;

n — кінцевий час прогнозування події.

Висновок: таким чином, в умовах повної невизначеності

суб’єкти господарської діяльності повністю не мають можливості

яким би то не було способом прогнозувати як перспективу свого

власного розвитку, так і ринку в цілому.

Повна визначеність характеризується близькою до 1 прогнос-

тичністю події:

1lim =

→

(2)

Висновок: повна визначеність дає можливість суб’єктам

господарської діяльності зі 100%-ною імовірністю прогнозувати

не тільки свою стратегію на ринку, але і його тенденції розвитку.

Часткова невизначеність характеризується імовірністю настан-

ня події, а отже, й ступенем її прогностичності в межах від 0 до 1:

1lim0 ≤≤

→nt

(3)

Часткова невизначеність для суб’єктів господарської діяльнос-

ті має конкретний практичний характер, на відміну від першого

та другого видів, які являють собою теоретичне припущення щодо

можливостей господарських суб’єктів.

Причини виникнення невизначеності

1. Недетермінованість процесів і, як наслідок, відсутність

можливості повного пророкування й прогнозування даних.

2. Відсутність повної інформації або її суб’єктивного аналізу

при плануванні поведінки (об’єкта) суб’єкта.

3. Вплив суб’єктивних факторів на результати проведених до-

сліджень (рівень кваліфікації працівників, які проводять аналіз,

величина тимчасового простору аналізованого періоду).

Останкова Л. А., Шевченко Н. Ю.

Виходячи з цього у процесі оцінки невизначеності й кількісного

визначення рівня ризику використовують імовірнісні розрахунки.

1.1.4. Системний аналіз економічного

ризику

Аналіз ризику — це методологія, за допомогою якої невизна-

ченість, властива найважливішим техніко-економічним показ-

никам (норма доходу, чиста приведена вартість), аналізується й

розглядається в контексті майбутніх періодів для оцінки впливу

ризику на відповідні результати.

Комплексний аналіз ризику містить:

— якісний аналіз ризику, тобто виявлення факторів ризику,

областей ризику, ідентифікація всіх можливих ризиків;

— формування системи кількісних показників рівня ризику;

— кількісний аналіз ризику, тобто чисельне визначення сту-

пеня окремих ризиків та ризику даного проекту в цілому;

— моделювання та прогнозування ризику;

— управління ризиком з метою зниження його впливу.

Системний підхід заснований на необхідності розглядати всі

явища та процеси в їх взаємозалежності, з урахуванням впливу

один на одного та зворотного зв’язку.

1.2. Застосування теорії корисності

в керуванні економічними ризиками

1.1.1. Основні визначення концепції

корисності [5–6]

Корисність W — певне число, яке приписується індивідом

кожному можливому результату. Корисність виражає ступінь за-

доволення, яке одержує суб’єкт у результаті споживання товару

або послуги.

Аналіз, моделювання та управління економічними ризиками

Функція корисності (функція Неймана-Моргенштерна)

U/W — показує корисність, яку приписує особа, яка приймає рі-

шення (ОПР), кожному можливому результату залежно від став-

лення до ризику.

Очікувана корисність події — сума добутків імовірностей ви-

никнення даної події (р

) на значення корисності (W

) її:

∑

(4)

Вибір ОПР (особи, яка приймає рішення) в умовах ризику фор-

малізується за допомогою поняття втрати, при цьому ОПР виявляє

свої індивідуальні смаки й схильність до ризику. Рішення її може

бути знайдене на основі наступного алгоритму:

— привласнюються довільні значення корисності виграшу

для кращого й гіршого наслідків, причому гіршому із на-

слідків ставиться у відповідність менше значення корис-

ності;

— гравцеві надається вибір: одержати певну гарантовану суму

W, що знаходиться в інтервалі між гіршим (s) і кращим (S)

значеннями виграшів

SWs <<

; взяти участь у грі (лоте-

реї), тобто одержати з імовірністю (1-р) найбільшу грошову

суму S і з імовірністю р одержати найменшу грошову суму

s, при цьому імовірність варто змінювати (зменшувати або

підвищувати) доти, доки ОПР не стане байдужою до вибору

між гарантованою сумою й грою.

Функція корисності має вигляд:

() (1- ) ( )WpUs pUS=+

, (5)

де р — задана імовірність.

Безумовний грошовий еквівалент (БГЕ) — максимальна сума

грошей, яку ОПР готовий заплатити за участь у грі (лотереї), або

мінімальна сума грошей, за якої він готовий відмовитися від гри.

Очікувана грошова оцінка (ОГО) — середній виграш у грі.

Висновок. Якщо БГЕ = ОГО

⇒ ОПР — об’єктивіст. Якщо

БГЕzОГО ⇒ ОПР — суб’єктивіст (якщо БГЕ>ОГО ⇒ ОПР —

схильний до ризику; якщо БГЕ<ОГО ⇒ ОПР — не схильний

до ризику).

Останкова Л. А., Шевченко Н. Ю.

Детермінований еквівалент лотереї

— це гарантована сума



, отримання якої еквівалентне участі в лотереї, тобто

Lx ≈



Отже,



визначається із рівняння:

)()],([)(

xMUuxɱɢxUMxU





. (6)

Особу, яка приймає рішення, називають не схильною до ри-

зику, якщо для неї більш пріоритетною є можливість отримати

гарантовано сподіваний виграш у лотереї, ніж брати в ній участь.

Премія за ризик — це сума, якою суб’єкт ризику згоден знехту-

вати із середнього виграшу за те, щоб уникнути ризику, пов’язаного

з лотереєю.

Страхова сума — величина детермінованого еквіваленту із

протилежним знаком.

Приклад. Гранична корисність зменшується з 15 одиниць,

якщо доход зростає від 0 до 1000 грн, до 10 одиниць, якщо доход

збільшується від 1000 грн до 2000 грн, та до 5 одиниць, якщо доход

зростає з 2000 до 3000 грн (рис. 1).

Припустимо, що людина з такою функцією корисності має до-

ход 1500 грн і оцінює нове місце роботи, яке пов’язане з ризиком.

Доход на новому місці роботи може бути більшим вдвічі, тобто

3000 грн, або менше на 500 грн, кожна альтернатива має ймовір-

ність

0,5p =

. Що має вчинити людина? Яке місце роботи слід об-

рати?

Із рис. 1 знаходимо, що корисність на старому місці роботи

складає 20 одиниць. Рівень корисності, що відповідає доходам

у 1000 грн, складає 15 одиниць, а рівень корисності, пов’язаний з

доходами у 3000 грн, дорівнює 30 одиниць.

Аналіз, моделювання та управління економічними ризиками

)(xU

1000 2000 3000 4000 5000

15 25 30 35

Рис. 1. Функція корисності особи, яка несхильна до ризику

Використовуючи формулу для розрахунку сподіваної корис-

ності, маємо:

11 2 2

[ ] ( ) ( ) 0,5 (1000) 0,5 (3000) 0,5 15 0,5 30 22,5UMU PUx PUx U U== + = + =⋅+⋅=

од.

Отже, нове місце роботи, яке пов’язане з ризиком, є більш прі-

оритетним, бо сподівана корисність

22,5U =

одиниць більша, ніж

корисність, пов’язана з тновим місцем роботи, яка становить лише

20 одиниць.

Отже, цій особі слід прийняти рішення про перехід на нове

місце роботи, хоча воно й пов’язане з ризиком.

Підрахуємо також винагороду за ризик

)(x

. Ми вже знаємо,

що сподівана корисність у 22,5 одиниць досягається при переході

на нове місце роботи. Сподіваний доход

)]([

при цьому складає

2000 грн Але, як видно з рис. 1, рівень корисності в 22,5 одиниць

може бути досягнутий, якщо стабільний доход цієї особи, тобто

детермінований еквівалент



, буде дорівнювати 1750 грн.

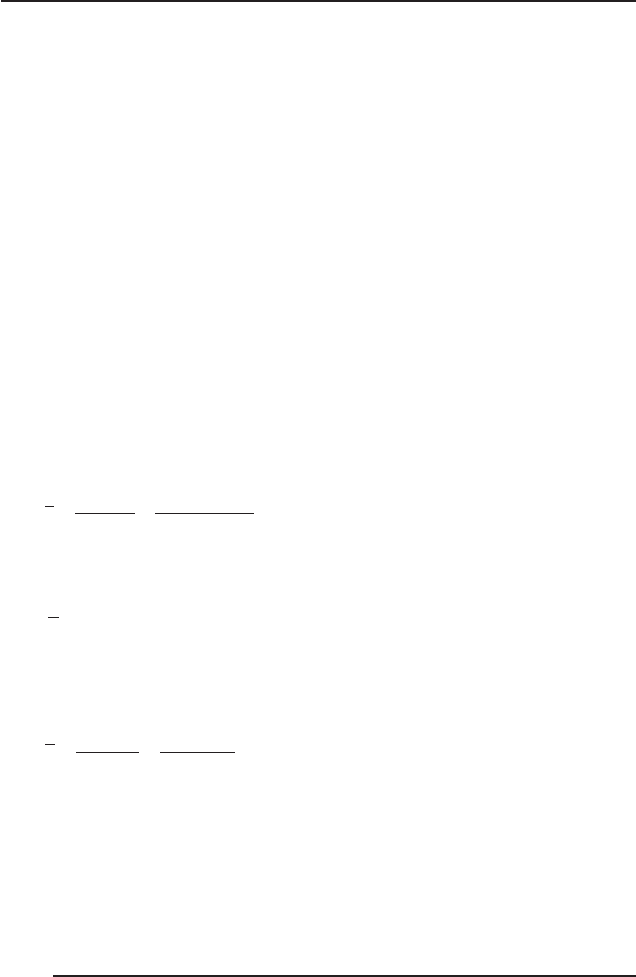
Останкова Л. А., Шевченко Н. Ю.

Премію за ризик визначають наступним чином:

xxMx



 )]([)(

25017502000)( =−=x

грн

Отже, 250 грн складає, власне, той розмір доходу, яким особа

готова знехтувати, вважаючи пріоритетнішою роботу з доходом

у 1750 грн, аніж з ризикованим.

Приклад. Особа, функція корисності якої зображена на рис. 1,

має декілька альтернативних варіантів, обираючи місце роботи.

Перше місце роботи пов’язане зі стабільним доходом у 2000 грн,

друге — з ризиком: мати доход у 3000 грн з імовірністю

0,5p =

, чи

доход у 1000 грн Третє місце роботи також пов’язане з ризиком:

мати доход 5000 грн з імовірністю

0,5p =

чи не мати ніякого до-

ходу. Яке місце роботи обрати даній особі?

На першому місці роботи зі стабільним доходом у 2000 грн осо-

ба має корисність доходу 25 одиниць.

При обранні другого місця роботи середній доход складає:

2000

10003000

грн і дорівнює доходові на першо-

му місці роботи.

Корисність при цьому дорівнює:

[ ] 0,5 (3000) 0,5 (1000) 0,5 30 0,5 15 22,5UMU U U== + =⋅+⋅=

од.

При обранні третього місця роботи сподіваний доход складає

2500 грн:

2500

05000

грн

Корисність при цьому складає:

Аналіз, моделювання та управління економічними ризиками

[ ] 0,5 (5000) 0,5 (0) 0,5 35 0,5 0 17,5UMU U U== + =⋅+⋅=

од.

Обираємо максимальну корисність:

{}

max 25;22,5;17,5 25=

од.

Отже, з трьох місць роботи слід обрати перше, де корисність

максимальна і доход стабільний.

1.2.2. Графік функції корисності

[2, 5–6, 13, 26]

Позначимо U (X) — корисність грошової суми

з точки зору

індивіда, тоді принциповий вид функції корисності має вигляд,

вказаний на рис. 2 [2, 5–6, 26].

Головна властивість графіка — опуклість, тобто приріст корис-

ності грошей зменшується зі збільшенням їхньої кількості.

Принцип Неймана — Моргенштерна. Індивід буде робити так,

щоб максимізувати очікуване значення корисності [13, 26].

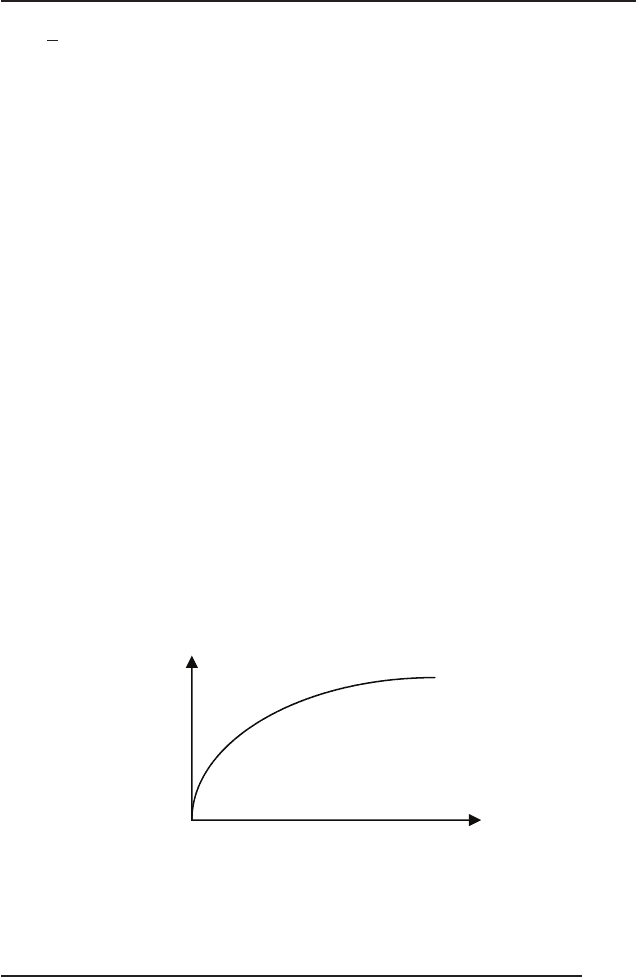
ОПР схильний до ризику тоді і тільки тоді, коли функція ко-

рисності має вигляд

0(x)U >

′′

(рис. 3).

)(xU

Рис. 2. Графічне зображення корисності

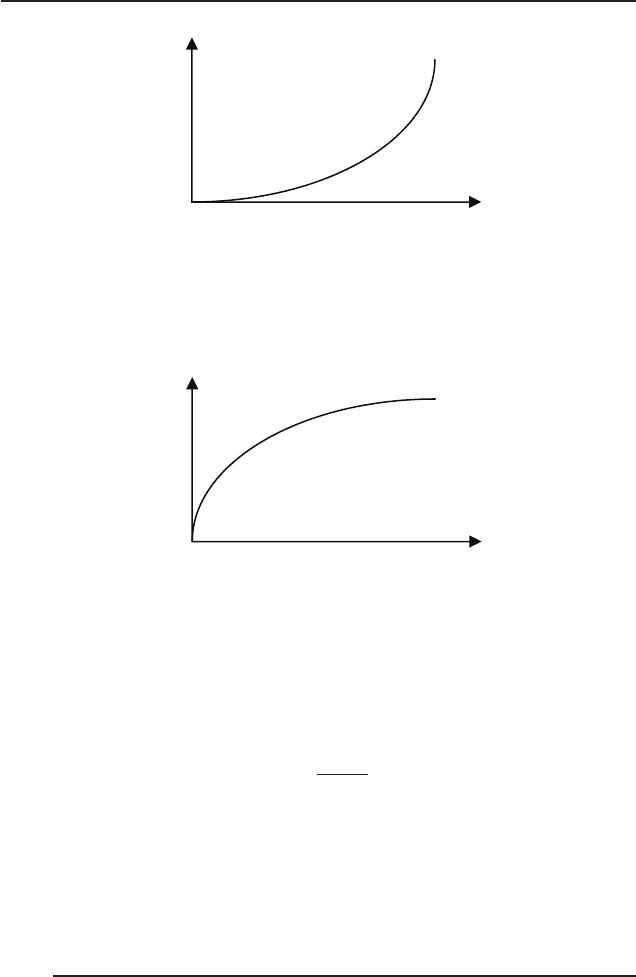
Останкова Л. А., Шевченко Н. Ю.

)(xU

Рис. 3. Функція корисності

0(x)U >

′′

ОПР несхильний до ризику тоді і тільки тоді, коли

0(x)U <

′′

(рис. 4).

)(xU

Рис. 4. Функція корисності

0(x)U <

′′

ОПР байдужий до ризику, тоді і тільки тоді, коли функція ко-

рисності лінійна, а графік функції — пряма лінія.

Для характеристики ставлення до ризику застосовується функ-

ція несхильності до ризику, що будується на основі функції корис-

ності і має вигляд:

()

′′

′

За допомогою даної функції можна дати найбільш повну ха-

рактеристику ставлення ОПР до ризику (табл. 1).

Аналіз, моделювання та управління економічними ризиками

Таблиця 1. Основні варіанти поведінки ОПР

Характеристики r (x) Ставлення до ризику ОПР

1. r > 0, Ě > 0

Зростаюча несхильність до ри-

зику

2. r > 0,

Ě < 0

Несхильність до ризику, що

зменшується

3. r > 0,

Ě = 0 (r = const > 0)

Постійна несхильність до ри-

зику

4. r < 0, Ě > 0

Схильність до ризику, що змен-

шується

5. r

< 0, Ě < 0

Зростаюча схильність до ризи-

ку

6. r < 0, Ě = 0 (r = const < 0)

Постійна схильність до ризику

= 0

Нейтральне ставлення до ри-

зику

1.2.3. Основні функції корисності [13, 26]

Основні функції корисності використовуються для вивчення,

аналізу та оцінки поведінки суб’єктів ризику:

0)(bbx;aU(x) !

— функція, що відображає нейтраль-

ність до ризику.

U(x) log (x b); (x –b, a 1)=+>>

— функція, що виражає

убутну несхильність до ризику.

-cx

U(x) –e ; (c 0)=>

— постійна несхильність до ризику.

U(x) –e ; (c 0)=>

— постійна схильність до ризику.

U(x) a bx–cx ; (c 0; x )

=+ > <

— зростаюча несхильність

до ризику.

U(x) –x ; (x 0)=<

— зростаюча схильність до ризику.

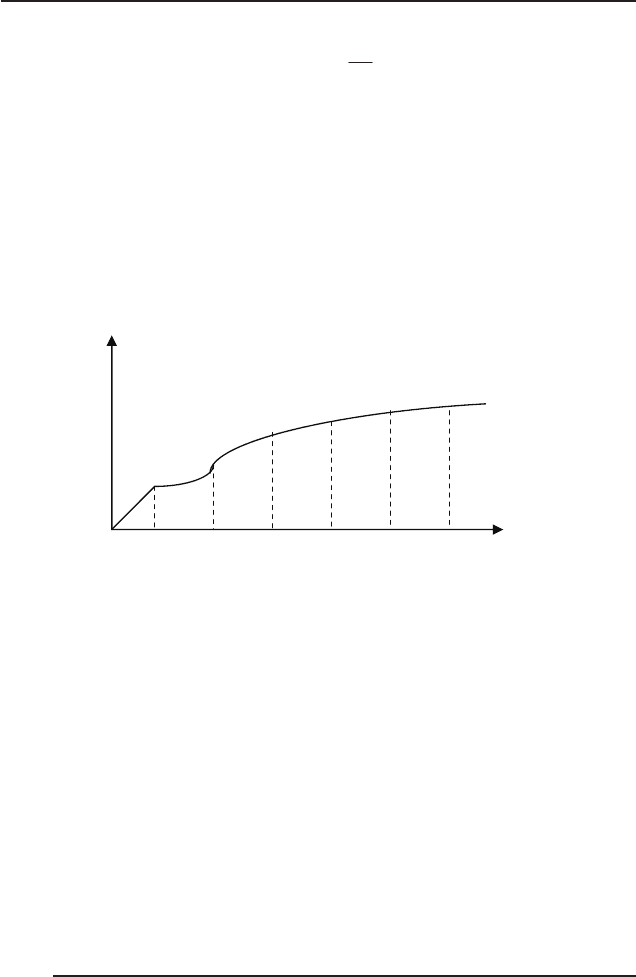
Останкова Л. А., Шевченко Н. Ю.

)

x0;(c;cxbxa

(x)

!!

— убутна схильність до ри-

зику.

8. Функція з інтервальною нейтральністю до ризику, що дозво-

ляє з будь-яким ступенем точності апроксимувати будь-яку функ-

цію корисності. Дану функцію зручно задавати графічно (рис. 5).

Одним із основних видів функції корисності, що характеризує

фінансову поведінку людей, є функція

lnxU(x) =

, тобто корис-

ність нескінченно малого виграшу прямо пропорційна цьому вигра-

шу й обернено пропорційна грошовій сумі, якою гравець володіє.

U(x) ]x[0;x

 - ɧɟɣɬɪɚɥɶɧɟ ɫɬɚɜɥɟɧɧɹ ɞɨ ɪɢɡɢɤɭ

0 ɯ

Рис. 5. Функція корисності з інтервальною нейтральністю

до ризику ОПР

Отже, якщо корисність описується функцією

lnxU(x) =

то втрати більш відчутні, ніж виграш.

1.2.4. Дерево рішень у контексті концепції

корисності [8]

Дерево рішень — графічне зображення послідовностей рішень

і стану середовища із зазначенням відповідних ймовірностей і ви-

грашів для будь-яких комбінацій, альтернатив (дій) та станів се-

редовища [8].