Patrick F. Dunn, Measurement, Data Analysis, and Sensor Fundamentals for Engineering and Science, 2nd Edition

Подождите немного. Документ загружается.

386 Measurement and Data Analysis for Engineering and Science

y(t)dt,

y(t) cos



2πnt



dt n = 1, 2, . . . , ∞,

(10.7)

and

y(t) sin



2πnt



dt n = 1, 2, . . . , ∞. (10.8)

Fourier analysis of a discrete signal is accomplished by replacing the follow-

ing in Equations 10.6 and 10.8:

1. The integrals over t in Equation 10.8 by summations over δt.

2. Continuous time t by discrete time rδt, where r = 1, 2, . . . , N.

3. T = Nδt, where N is an even number.

4. n from 1 to ∞ with k from 0 to N/2.

In doing so, A

becomes a

, where

Nδt

r=1

y(rδt) cos



2πkrδt

Nδt



δt

r=1

y(rδt) cos



2πkr



k = 0, 1, . . . ,

. (10.9)

Likewise,

r=1

y(rδt) sin



2πkr



k = 1, 2, . . . ,

− 1 (10.10)

and

r=1

+ b

. (10.11)

Note that k represents the discrete frequency and r the discrete sample

point. Each discrete sample point can contribute to a discrete frequency.

Every sample point’s contribution to a particular discrete frequency is in-

cluded by summing over all sample points at that frequency. This yields the

corresponding discrete expression for y(t),

Signal Analysis 387

y(rδt) =

(N/2)−1

k=1



cos



2πrk



+ b

sin



2πrk



N/2

cos(πr). (10.12)

The last term corresponds to f

max

= f

. The equations for a

and b

comprise the discrete Fourier transform or DFT of y(rδt). The equation

y(rδt) is the discrete Fourier series.

A computer program or M-ﬁle can be written to perform the DFT, which

would include the following steps:

1. Fix k.

2. Evaluate 2πrk/N for all r.

3. Compute cos[2πrk/N] and sin[2πrk/N ].

4. Compute y(rδt) cos[2πrk/N] and y(rδt) sin[2πrk/N].

5. Sum these values from r = 1 to N to give a

and b

as given in Equations

10.9 and 10.10.

6. Repeat for next k

7. After completing for all k, determine c

using Equation 10.11.

This method involves N

real multiply-add operations.

Alternatively, the DFT can be written using complex notation. Using the

Fourier coeﬃcient deﬁnitions in Equation 10.8, and introducing Y

, which

was called C

in Chapter 9, gives

− i

. (10.13)

This leads to

(t) =

y(t)



cos



2πnt



− i sin



2πnt



y(t) exp[−i(2πnt/T )]dt. (10.14)

By making the appropriate substitutions for T , δt, and n in Equation 10.14,

the discrete Fourier transform in complex form becomes

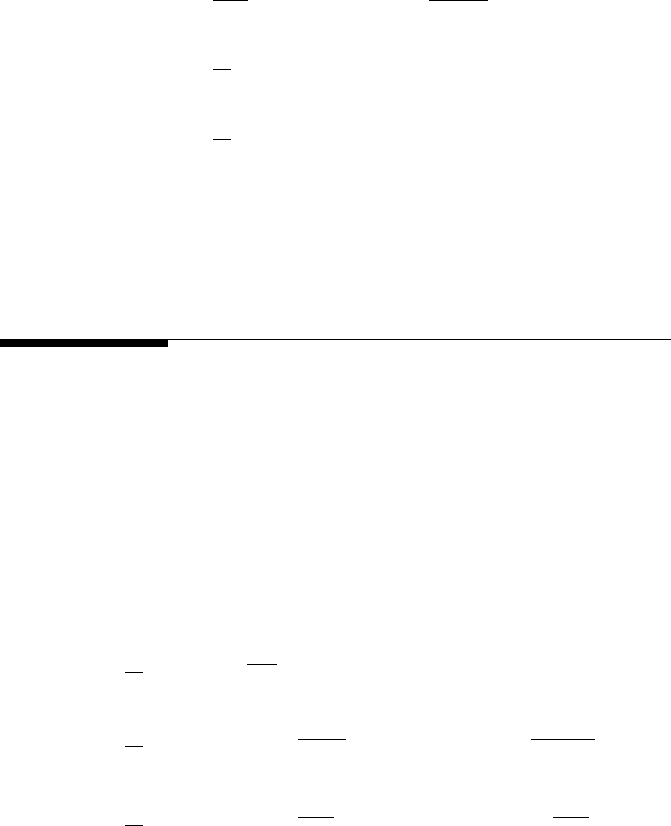
388 Measurement and Data Analysis for Engineering and Science

Nδt

r=1

y(rδt) exp



−i



2πkrδt

Nδt



r=1

y(rδt) exp[−i(2πkr/N)]

r=1

exp[−i(2πkr/N)]. (10.15)

Again, k represents the discrete frequency and r represents the discrete

sample point. This method requires N

complex multiplications. Note also

that 2πrk/N can be replaced by 2πrf

δt because f

= k/T = k/(N δt).

10.5 Fast Fourier Transform

The fast Fourier transform, or FFT, is a speciﬁc type of DFT that is

computationally faster than the original DFT. Danielson and Lanczos pro-

duced one such FFT algorithm in 1942. Cooley and Turkey developed the

most frequently used one in the mid-1960’s. Danielson and Lanczos showed

that a DFT of length N can be rewritten as the sum of two DFTs, each of

length N/2, one coming from the even-numbered points of the original N,

the other from the odd-numbered points [3]. Equation 10.15 can be rear-

ranged to conform to this format as

N−1

r=0

−i

(

2πrk

)

(10.16)







(N/2)−1

r=0

−i

[

2π(2r)k

]

(N/2)−1

r=0

2r+1

−i

[

2π(2r+1)k

]













(N/2)−1

r=0

−i

[

2πrk

(N/2)

]

+ W

(N/2)−1

r=0

2r+1

−i

[

2πrk

(N/2)

]







where W

≡ e

−i[2πk/N]

. Equation 10.17 can be written in a more condensed

form, Y

= Y

even

+ W

odd

, where Y

even

is the kth component of the

DFT of length N/2 formed from the even-numbered y

values and Y

odd

the kth component of the DFT of length N/2 formed from the odd-numbered

values. This approach can be applied successively until the last transforms

Signal Analysis 389

FIGURE 10.6

DFT sequence for N = 8.

FIGURE 10.7

DFT sequence for N = 8 showing bit reversal.

have only one term each. At that point, the DFT of the term equals the term

itself, where Y

(for k = 0, r = 0, N = 1) = (1/1) y

−i·0

= y

= Y

The sequence of the computational breakdown for N = 8 is displayed

in Figure 10.6. Symmetry is maintained when N = 2

. Here Y

xxx

are the

DFTs of length one. They equal the values of the discrete sample points,

y(rδt). For a given N, the particular y

values can be related to a pattern

of e’s and o’s in the sequence. By reversing the pattern of e’s and o’s (with

e = 0 and o = 1), the value of k in binary is obtained. This is called bit

reversal. This process is illustrated in Figure 10.7. The speed of this FFT is

∼ O(N log

N) vs O(N

) for the DFT, which is approximately 40 000 times

faster than the original DFT!

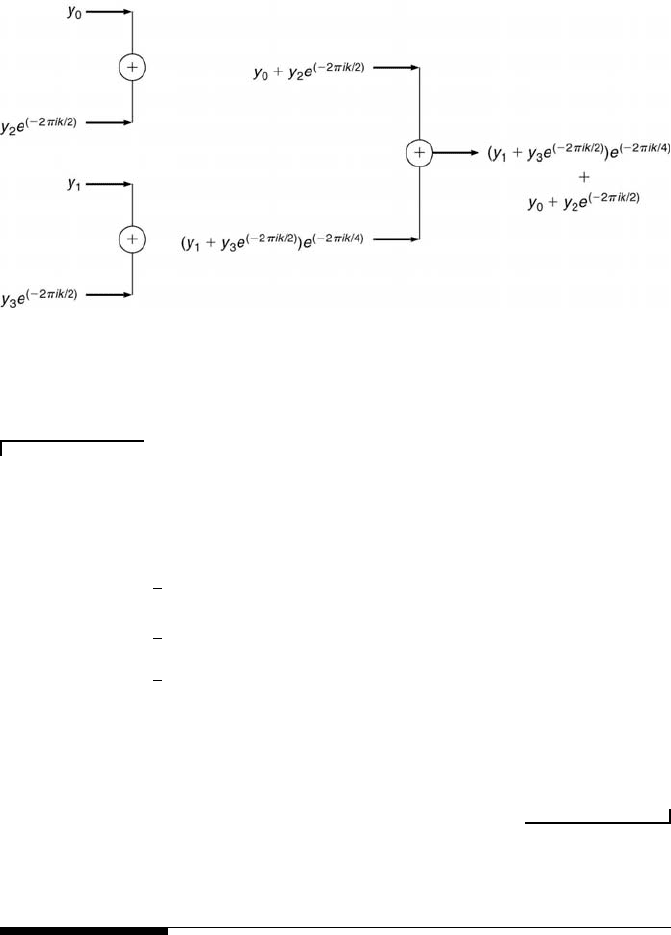
390 Measurement and Data Analysis for Engineering and Science

FIGURE 10.8

More eﬃcient DFT sequence for N = 4.

Example Problem 10.3

Statement: For the case of N = 4, determine the four DFT terms y

, y

and

for r = 0, . . . , N − 1.

Solution: Direct implementation of Equation 10.17 yields

r=0

−i(2πrk/4)

+ y

−i(2πk/4)

+ y

−i(2π2k/4)

+ y

−i(2π3k/4)

+ y

−i(2πk/2)

+ e

−i(2πk/4)

+ y

−i(2πk/2)

Thus, the DFT could be performed computationally faster in the sequence, as

illustrated in Figure 10.8, by starting with the even (y

and y

) and odd (y

and y

)

pairs.

10.6 Amplitude Ambiguity

Amplitude ambiguity also arises when the sample time period, T

, is not

an integer multiple of the fundamental period of the signal. If the signal

has more than one period or is aperiodic, this will complicate matters. For

complex periodic signals, T

must be equal to the least common integer

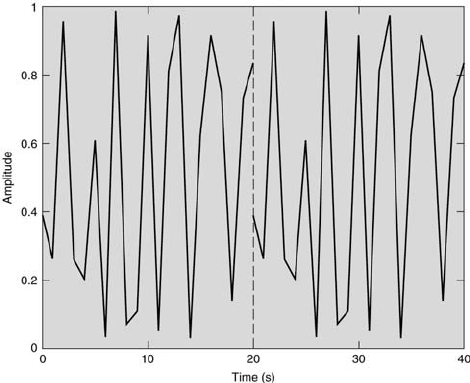
Signal Analysis 391

FIGURE 10.9

Two repeated segments of the same random signal.

multiple of all frequencies contained in the signal. For aperiodic signals,

theoretically must be inﬁnite. Practically, ﬁnite records of length T

are

considered and windowing must be used to minimize the eﬀect of amplitude

ambiguity. Application of the DFT or FFT to an aperiodic signal implicitly

assumes that the signal is inﬁnite in length and formed by repeating the

signal of length T

an inﬁnite number of times. This leads to discontinuities

in the amplitude that occur at each integer multiple of T

, as shown in

Figure 10.9 at the time equal to 20 s. These discontinuities are step-like,

which introduce false amplitudes that decrease around the main frequencies

similar to those observed in the Fourier transform of a step function (see

Chapter 9).

Thus, the amplitudes of simple or complex periodic waveforms will be

accurately represented in the DFT when f

> 2f

max

and T

= mT

, where

m = 1, 2, ...,. T

is the fundamental period (= 1/f

) and T

the total sample

period (= Nδt = N/f

), which implies that N = m(f

). If the latter con-

dition is not met, leakage will occur in the DFT, appearing as amplitudes

at f

spilling over into other adjacent frequencies. Further, for DFT compu-

tations to be fast, N must be set equal to 2

, which yields 2

= m(f

where m and N are positive integers. These conditions are summarized as

follows:

1. Set f

max

= f

⇒ f

= 2f

max

, assuming that f

and f

max

are known.

2. Find a suitable N by the steps:

(a) Choose a value for m, keeping m ≥ 10).

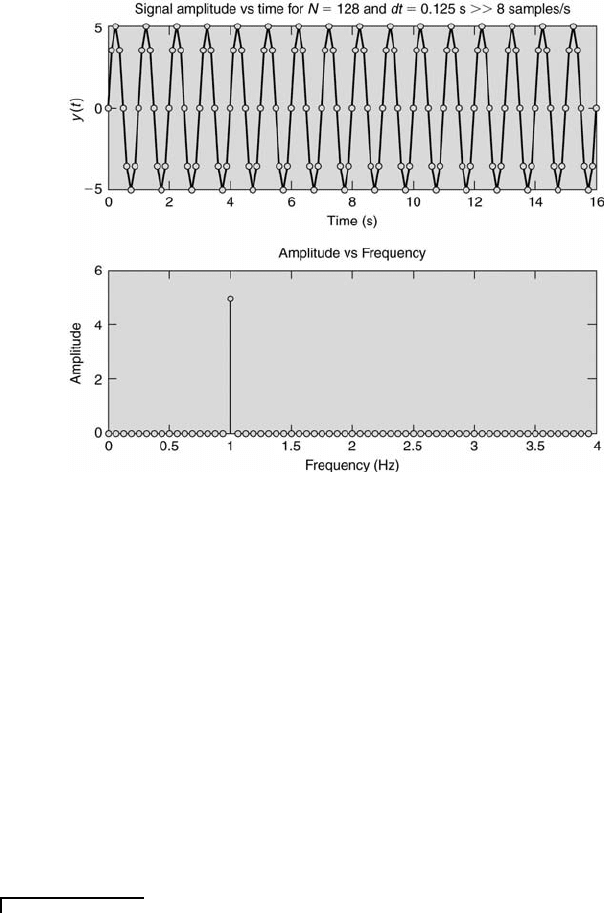
392 Measurement and Data Analysis for Engineering and Science

FIGURE 10.10

Signal and frequency spectrum with dt = 0.125 s.

(b) Is there an integer solution for M, where 2

= m(f

(d) If not, iterate until an integer M is found. Thus, N = 2

and

= Nδt.

For aperiodic and nondeterministic waveforms, the frequency resolution δf

(= 1/Nδt) is varied until leakage is minimized. Sometimes, all frequencies

are not known. In that case, to avoid leakage, windowing must be used.

The following example illustrates the eﬀect of sampling rate on the result-

ing amplitude-frequency spectrum in terms of either aliasing or amplitude

ambiguity.

Example Problem 10.4

Statement: Convert the analog voltage, E(t) = 5 sin(2πt) mV, into a discrete time

signal. Speciﬁcally, using sample time increments of (a) 0.125 s, (b) 0.30 s, and (c)

0.75 s, plot each series as a function of time over at least one period. Discuss apparent

diﬀerences between the discrete representation of the analog signal. Also, compute the

DFT for each of the three discrete signals. Discuss apparent diﬀerences. Use a data set

of 128 points.

Solution:

y(t) = 5 sin(2πt) ⇒ f = 1 Hz.

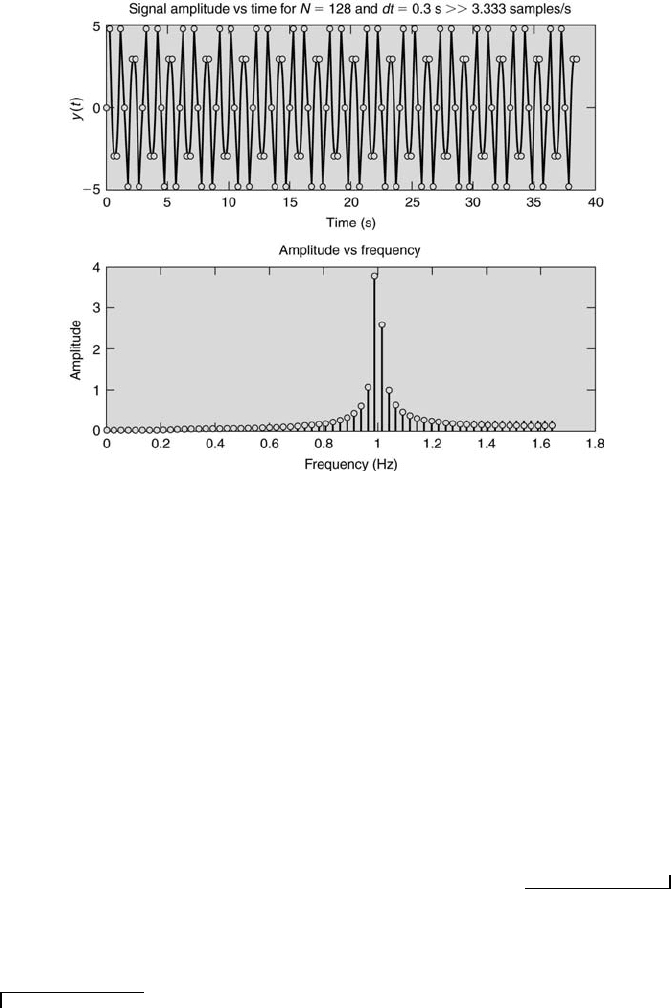
Signal Analysis 393

FIGURE 10.11

Signal and frequency spectrum with dt = 0.3 s.

Aliasing will not occur when f

(= 1/dt) > 2f (f = 1 Hz). Amplitude ambiguity

will not occur when T = mT

⇒ m = f Ndt (m : integer).

For part (a) f

> 2f and m = (1)(128)(.125) = 16 ⇒ no aliasing or amplitude

ambiguity. The result is shown in Figure 10.10, which was presented previously to

illustrate the FFT.

For part (b) f

> 2f ⇒ no aliasing, and m = (1)(128)(0.3) = 38.4 ⇒ amplitude

ambiguity will occur. This is displayed in Figure 10.11. The amplitude, however, is less

than the actual amplitude (here it is less than 4). Around that frequency the amplitude

appears to leak into adjacent frequencies.

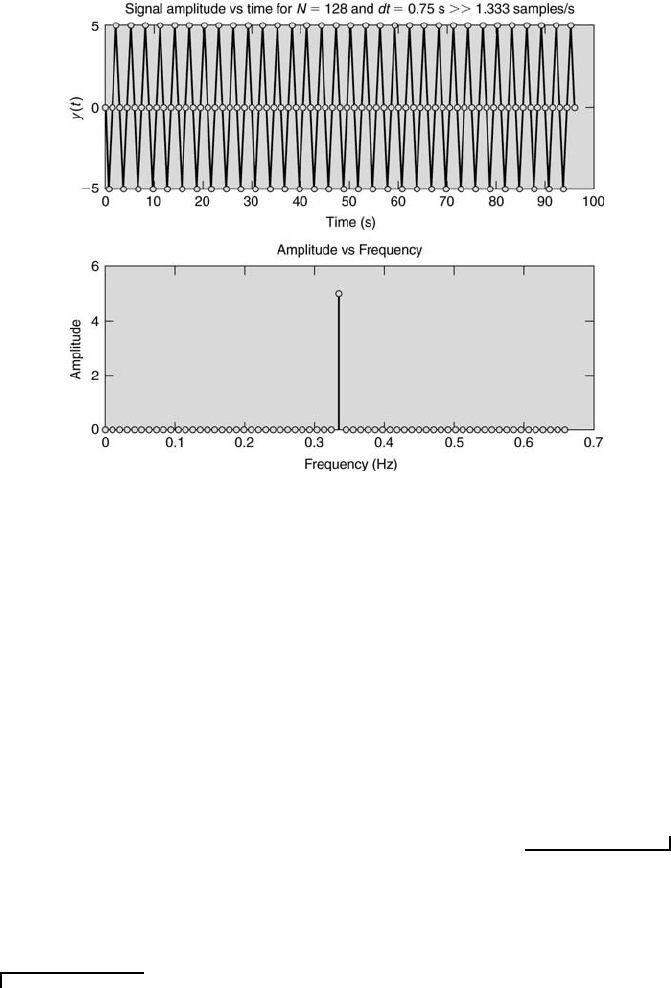
For part (c) f

< 2f ⇒ aliasing will occur, and m = (1)(128)(0.75) = 96 ⇒ no

amplitude ambiguity will be present. This is shown in Figure 10.12. The aliased fre-

quency can be determined using the aforementioned folding-diagram procedure. Here,

= 4/3, f

= 2/3, and f = 1. This leads to k = 3/2, which implies k

= 1/2 using

the folding diagram. Thus, f

= (1/2)(2/3) = 1/3 Hz.

Now consider an example where both aliasing and amplitude ambiguity

can occur simultaneously.

Example Problem 10.5

Statement: Compute the DFT for the discrete time signal that results from sam-

pling the analog signal, T (t) = 2 sin(4πt)

◦

C, at sample rates of 3 Hz and 8 Hz. Use a

data set of 128 points. Discuss and compare your results.

394 Measurement and Data Analysis for Engineering and Science

FIGURE 10.12

Signal and frequency spectrum with dt = 0.75 s.

Solution:

T (t) = 2 sin(4πt) ⇒ 2 Hz.

For the sample rate of 3 Hz, f

= 2f ⇒ aliasing will occur and m = (1)(128)(1/3) =

42.67 ⇒ amplitude ambiguity will be present. The results are presented in Figure 10.14.

The aliased frequency occurs where the amplitude is maximum, at 1 Hz. This can

be determined using the aforementioned folding-diagram procedure. Here, f

= 3,

= 3/2, and f = 2. This leads to k = 4/3, which implies k

= 2/3 using the folding

diagram. Thus, f

= (2/3)(3/2) = 1. Also, note the distortion of the signal’s time

record that occurs because of the low sampling rate.

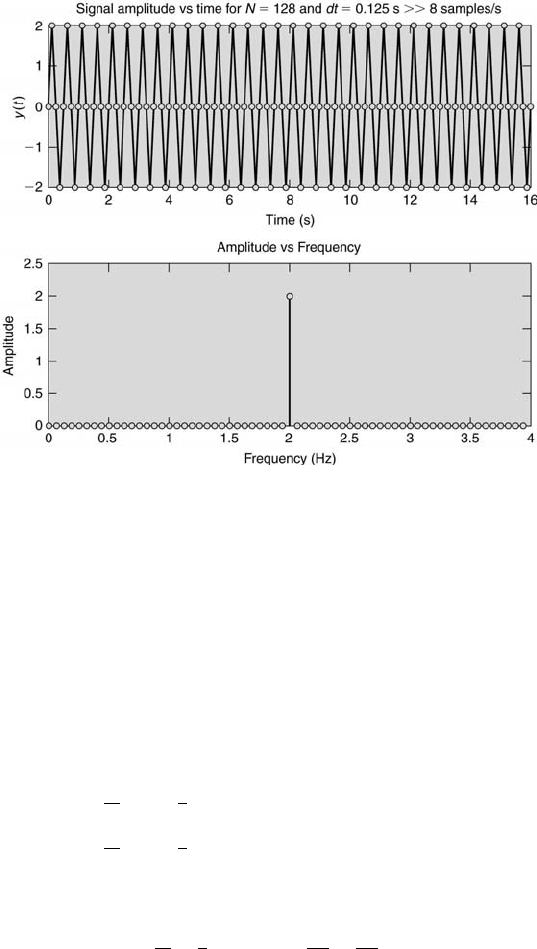
When the sampling rate is increased to 8 Hz, f

> 2f ⇒ no aliasing occurs.

Also m = (1)(128)(0.125) = 16 ⇒ no amplitude ambiguity occurs. This is shown in

Figure 10.13, which is the correct spectrum.

Analysis becomes more complicated when more than one frequency is

present in the signal. Next, consider an example that involves a signal con-

taining two frequencies.

Example Problem 10.6

Statement: Consider the signal y(t) = 3.61 sin(4πt + 0.59) + 5 sin(8πt). Plot y(t)

versus time and the resulting frequency spectrum for the following cases and discuss

what is observed with respect to aliasing and amplitude ambiguity:

Signal Analysis 395

FIGURE 10.13

Signal and frequency spectrum with dt = 0.125 s.

(i) N = 100, f

= 50

(ii) N = 20, f

= 10

(iii) N = 10, f

= 5

(iv) N = 96, f

= 5

(v) N = 96, f

= 10

Solution: y(t) = 3.61 sin(4πt + 0.59) + 5 sin(8πt). So, f

= 2 Hz and f

= 4 Hz,

which implies that f

max

= 4 Hz. If f

= 5 samples/s,

= 2.5 > 2 ⇒ no aliasing, and

= 1.25 < 2 ⇒ aliasing will occur.

To where will the 4 Hz component be aliased?

= 2.5 Hz ⇒

2.5

= 1.6.

Using the folding diagram 1.6f

is folded down to 0.4f

= (0.4)(2.5) = 1 Hz. That is,

the 4 Hz component appears as a 1 Hz component.

But what about amplitude ambiguity? T

= 1/f

= 1/2 s, and T

= 1/f

= 1/4 s.

The total sample period, T , must contain integer multiples of both T

and T

so as not

to have amplitude ambiguity in both components. This can be easily met by having

T = mT

= m/2 s (since T

= T

/2). In essence, the least common integer multiple