Patrick F. Dunn, Measurement, Data Analysis, and Sensor Fundamentals for Engineering and Science, 2nd Edition

Подождите немного. Документ загружается.

376 Measurement and Data Analysis for Engineering and Science

13. Consider the signal

y (t) = A cos (ω

t) + A cos (ω

t) ,

where ω

= 56/500 rad/hr and ω

is 8 % greater in magnitude than ω

(a) What is the period of the corresponding slow beat in minutes (the

formal deﬁnition of slow beat)? (b) What is the period at which the slow

beat manifests itself in the output signal in minutes?

14. The following problems use the data ﬁle signal.dat that contains two

columns of data, each with 5000 rows (the ﬁrst column is the measured

velocity in m/s, and the second column is the sample time in s). The

velocities were measured behind an obstruction that contained several

cables of diﬀerent diameters. The data was taken over a period of 5 s

at a sample rate of 1 kHz (1000 samples/s). Assume that the sample

rate was fast enough such that the sampled signal represents the actual

signal in terms of its amplitude and frequency. The following M-ﬁles may

be useful: propintime.m and sstol.m. Write a program or spreadsheet

for this problem. (a) Plot the velocities versus time for the ﬁrst 250 ms

using points (dots) for each data point. (b) Plot the running mean and

running rms versus time. (c) Determine the times at which the running

mean and also the running rms for them to remain within 1 %, 2 %, 3

%, and 4 % of their ﬁnal values. Note that there will be diﬀerent times

for each running value for each percent tolerance.

15. Determine the rms of one period of a square wave in which y(t) = 0

from t = 0 to t = 0.5 and y(t) = 2 from t > 0.5 to t = 1.0.

Bibliography

[1] Merriam-Webster OnLine Collegiate Dictionary at http://www.m-

w.com/.

[2] Bendat, J.S. and A.G. Piersol. 1986. Random Data: Analysis and Mea-

surement Procedures. 2nd ed. New York: John Wiley and Sons.

[3] Oppenheim, A.V. and A.S. Willsky. 1997. Signals & Systems. 2nd ed.

New Jersey: Prentice Hall.

377

This page intentionally left blank

Signal Analysis

CONTENTS

10.1 Chapter Overview . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 379

10.2 Digital Sampling . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 380

10.3 Aliasing . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 382

10.4 Discrete Fourier Transform . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 385

10.5 Fast Fourier Transform . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 388

10.6 Amplitude Ambiguity . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 390

10.7 *Windowing . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 399

10.8 Problem Topic Summary . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 403

10.9 Review Problems . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 403

10.10 Homework Problems . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 403

For even the most stupid of men, by some instinct of nature, by himself and

without any instruction (which is a remarkable thing), is convinced that the

more observations have been made, the less danger there is of wandering

from one’s goal.

Jacob Bernoulli. 1713. Ars Conjectandi.

10.1 Chapter Overview

Today, most data is acquired and stored digitally. This format is advan-

tageous because of relatively rapid acquisition rates and minimal storage

requirements. Digital data acquisition, however, introduces errors. Fortu-

nately, these can be minimized with some foresight. So, how are signal ac-

quisition and analysis done digitally? What errors are introduced? How can

these errors be minimized such that the acquired information truly repre-

sents that of the process under investigation? Such questions are addressed

and answered in this chapter.

379

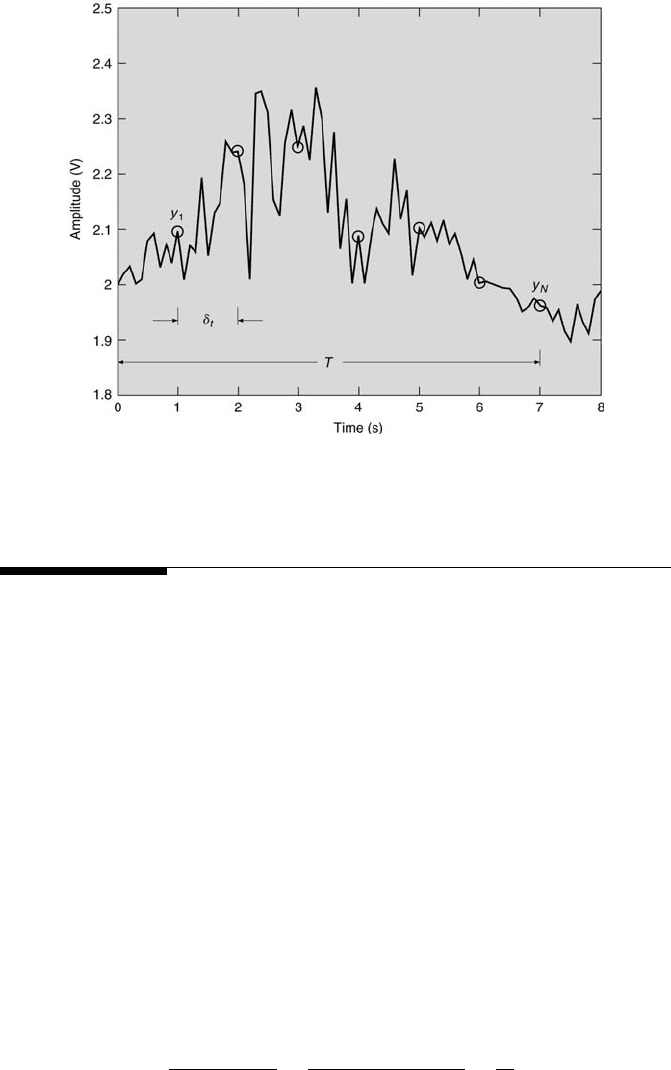
380 Measurement and Data Analysis for Engineering and Science

FIGURE 10.1

Discrete sampling of an analog signal.

10.2 Digital Sampling

Consider the analog signal, y(t), shown in Figure 10.1 as a solid curve. This

signal is sampled digitally over a period of T seconds at a rate of one sample

every δt seconds. The resulting discrete signal, y(rδt), is comprised of the

analog signal’s amplitude values y

through y

at the times rδt, where

r = 1, 2, ..., N for N samples. The discrete signal is represented by circles in

Figure 10.1. The accurate representation of the analog signal by the discrete

signal depends upon a number of factors. These include, at a minimum, the

frequency content of y(t), the time-record length of the signal, T = Nδt,

and the frequency at which the signal is sampled, f

= 1/δt = N/T .

Further assume that the signal contains frequencies ranging from 0 to

W Hz, which implies that the signal’s bandwidth is from 0 to W Hz.

The minimum resolvable frequency, f

min

, will be 1/T = 1/(Nδt). If the

sampling rate is chosen such that f

= 2W , then, as will be seen shortly,

the maximum resolvable frequency, f

max

, will be W = 1/(2δt). Thus, the

number of discrete frequencies, N

, that can be resolved from f

min

to f

max

will be

max

− f

min

δf

1/(2δt) − 1/(Nδt)

1/(Nδt)

− 1. (10.1)

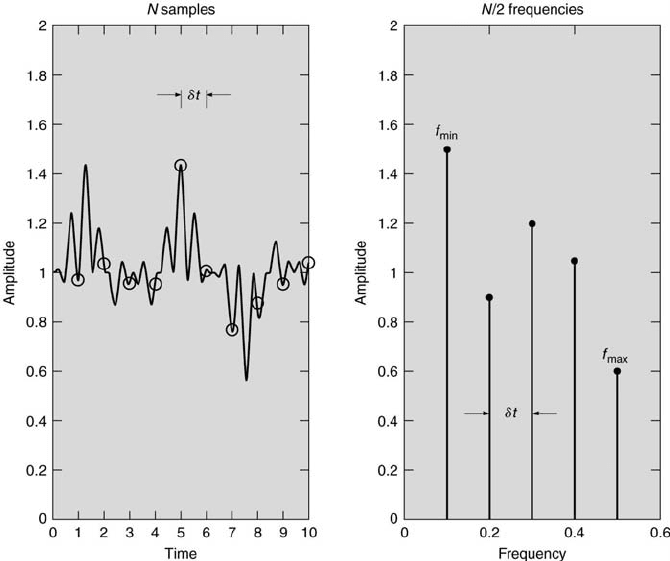
Signal Analysis 381

FIGURE 10.2

Amplitude-time-frequency mapping.

This implies that there will be N/2 discrete frequencies from f

min

to and

including f

max

. This process is illustrated in Figure 10.2.

Situations arise which introduce errors into the acquired information. For

example, if the sampling frequency is too low, the discrete signal will contain

false or alias amplitudes at lower frequencies, which is termed aliasing.

Further, if the total sample period is not an integer multiple of all of the

signal’s contributory periods, amplitude ambiguity will result. That is,

false or ambiguous amplitudes will occur at frequencies that are immediately

adjacent to the actual frequency. Thus, by not using the correct sampling

frequency and sampling period, incorrect amplitudes and frequencies result.

This, obviously, is undesirable.

How can these problems be avoided? Signal aliasing can be eliminated

simply by choosing a sampling frequency, f

, equal to at least twice the

highest frequency, f

max

, contained in the signal. However, it is diﬃcult to

avoid amplitude ambiguity. Its eﬀect only can be minimized. This is accom-

382 Measurement and Data Analysis for Engineering and Science

FIGURE 10.3

Frequency map to illustrate aliasing.

plished by reducing the magnitude of the signal at the beginning and the

end of the sample period through a process called windowing.

To fully understand each of these eﬀects, the discrete version of the

Fourier transform must be considered. This transform yields the amplitude-

frequency spectrum of the discrete data. The spectrum can be determined

for the discrete representation of a known periodic signal, which best illus-

trates the eﬀects of aliasing and amplitude ambiguity.

10.3 Aliasing

Ambiguities arise in the digitized signal’s frequency content whenever the

analog signal is not sampled at a high enough rate. Shannon’s sampling

theorem basically states that for aliasing not to occur, the signal should be

sampled at a frequency which is greater than twice the maximum frequency

contained in the signal, which often is termed the maximum frequency of

interest. That is, f

> 2f

max

. At the sampling frequency f

= 2f

max

, f

max

also is known as the Nyquist frequency, f

. So, f

= 2f

To illustrate analytically how aliasing occurs, consider the two signals

(t) = cos(2πf

t) and y

(t) = cos(2πf

t), in which f

is chosen subject

to two conditions: [1] f

= 2mf

± f

with m = 1, 2, ..., and [2] f

> f

These conditions yield speciﬁc f

frequencies above the Nyquist frequency,

all of which alias down to the frequency f

. The resulting frequencies are

displayed on the frequency map shown in Figure 10.3.

Assume that these two periodic signals are sampled at δt time incre-

ments, r times. Then

(t) = cos(2πf

t) becomes y

(rδt) = cos(2πrf

), (10.2)

and

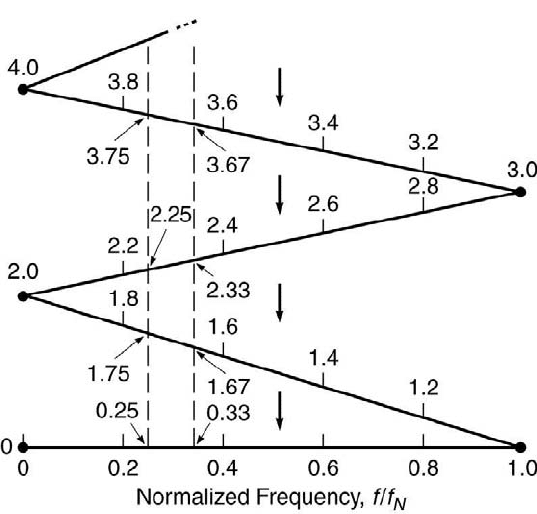
Signal Analysis 383

FIGURE 10.4

The folding diagram.

(t) = cos(2πf

t) becomes y

(rδt) = cos(2πrf

). (10.3)

Further reduction of Equation 10.3 reveals that

(rδt) = cos(2πr[2mf

± f

]/f

)

= cos(2πrm ± 2πrf

)

= cos(2πr(m ± f

))

= cos(2πrf

)

= y

(rδt). (10.4)

Thus, the sampled signal y

(rδt) will be identical to the sampled signal

(rδt), and the frequencies f

and f

will be indistinguishable. In other

words, all of the signal content at the f

frequencies will appear at the f

frequency. Their amplitudes will combine in quadrature with the signal’s

original amplitude at frequency f

, thereby producing a false amplitude at

frequency f

When aliasing occurs, the higher f

frequencies can be said to fold into

the lower frequency f

. This mapping of the f

frequencies into f

is illus-

384 Measurement and Data Analysis for Engineering and Science

trated by the folding diagram, as shown in Figure 10.4. The frequency, f

into which a frequency f is folded, assuming f > f

, is identiﬁed as follows:

1. Determine k, where k = f/f

. Note that f

= f

max

= f

/2.

2. Find the value k

that k folds into, where k

occurs on the bottom line

(0 ≤ k

≤ 1).

3. Calculate f

, where f

= k

The following example illustrates aliasing.

Example Problem 10.1

Statement: Assume that there is an analog signal whose highest frequency of in-

terest is 200 Hz (=f

), although there may be frequencies higher than that contained

in the signal. According to the sampling theorem, the sampling frequency must be set

at f

> 400 Hz for the digitized signal to accurately represent any signal content at

and below 200 Hz. However, the signal content above 200 Hz will be aliased. At what

frequency will an arbitrary aliased frequency appear?

Solution: According to the folding diagram, for example, the f

frequencies of

350 (1.75f

), 450 (2.25f

), 750 (3.75f

), and 850 (4.25f

), all will map into

= 50 Hz (0.25f

). Likewise, other frequencies greater than f

will map down

to frequencies less than f

. A frequency of 334 Hz will map down to 67 Hz, and so

forth.

Thus, for aliasing of a signal not to occur and for the digitized signal not

to be contaminated by unwanted higher-frequency content, f

ﬁrst must be

identiﬁed and then set such that f

> 2f

. Second, a ﬁlter must be used

to eliminate all frequency content in the signal above f

. In an experiment,

this can be accomplished readily by ﬁltering the signal with an anti-alias

(low-pass) ﬁlter prior to sampling, with the ﬁlter cut oﬀ set at f

Example Problem 10.2

Statement: The signal y(t) = sin(2π10t) is sampled at 12 Hz. Will the signal be

aliased and, if so, to what frequency?

Solution: Here f = 10 Hz. For signal aliasing not to occur, the signal should be

sampled at a frequency that is at least twice the maximum frequency of interest. For

this case, the required sampling frequency would be higher than 20 Hz. Because the

signal actually is sampled at only 12 Hz, aliasing will occur. If f

= 12 Hz, then f

= 6

Hz, which is one-half of the sampling frequency. Thus, k = f /f

= 10/6 = 1.67.

This gives k

= 0.33, which implies that f

= 0.33f

= (0.33)(6) = 2 Hz. So, the

aliased signal will appear as a sine wave with a frequency of 2 Hz. This is illustrated

in Figure 10.5.

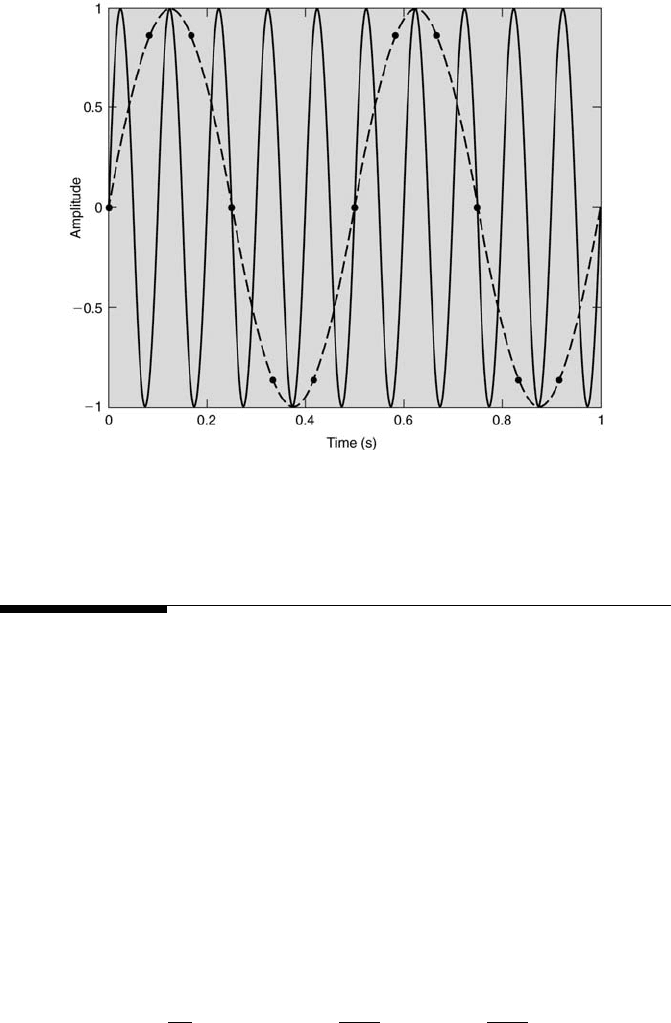
Signal Analysis 385

FIGURE 10.5

Aliasing of y(t) = sin(2π10t) (solid curve is y(t); dashed curve is aliased signal

from sampling at 12 Hz).

10.4 Discrete Fourier Transform

The discrete Fourier transform is a method used to obtain the frequency

content of a signal by implementing the discrete version of the Fourier trans-

form. A more detailed discussion of the discrete and fast Fourier transforms

is presented in [2].

Consider a sample of the signal y(t) with a ﬁnite record length, T , which

is its fundamental period. This signal is sampled N times at δt increments of

time. N values of the signal are obtained, y

= y(rδt), where r = 1, 2, ..., N.

The discrete signal becomes

y(rδt) = y(t) ·

δ(t − rδt). (10.5)

The impulse function,

δ, is deﬁned such that

δ(0) = 1 and

δ(6= 0) = 0.

Now recall the Fourier series representation of y(t),

y(t) =

∞

n=1



cos



2πnt



+ B

sin



2πnt



, (10.6)

with the Fourier coeﬃcients given by