Patrick F. Dunn, Measurement, Data Analysis, and Sensor Fundamentals for Engineering and Science, 2nd Edition
Подождите немного. Документ загружается.


356 Measurement and Data Analysis for Engineering and Science
FIGURE 9.8
Even and odd functions.
2. y(t) has a finite average value.
3. y(t) has a finite number of relative maxima and minima within the
period T .
If these conditions are met, then the series converges to y(t) at the values of
t where y(t) is continuous and converges to the mean of y(t
+
) and y(t
−
) at
a finite discontinuity. Fortunately, these conditions hold for most situations.
Recall that a periodic function with period T satisfies y(t + T ) = y(t) for
all t. It follows that if y(t) is an integrable periodic function with a period
T , then the integral of y(t) over any interval of length T has the same value.
Hence, the limits from −T /2 to T /2 of the Fourier coefficient integrals can
be replaced by, for example, from 0 to T or from −T/4 to 3T /4. Changing
these limits sometimes simplifies the integration procedure.
The process of arriving at the Fourier coefficients also can be simplified
by examining whether the integrands are either even or odd functions. Ex-
ample even and odd functions are shown in Figure 9.8. If y(t) is an even
function, where it is symmetric about the y-axis, then g(x) = g(−x). Thus,
Z
T
−T
g(x)dx = 2
Z
T
0
g(x)dx. (9.28)
The cosine is an even function. Likewise, if y(t) is an odd function, where
it is symmetric about the origin, then g(x) = −g(−x). So,

Signal Characteristics 357
Z
T
−T
g(x)dx = 0. (9.29)
The sine is an odd function. Other properties of even and odd functions
include the following:
1. The sum, difference, product, or quotient of two even functions is even.
2. The sum or difference of two odd functions is odd.
3. The product or quotient of two odd functions is even.
4. The product or quotient of an even function and an odd function is odd.
5. The sum or difference of an even function and an odd function is neither
even nor odd, unless one of the functions is identically zero.
6. A general function can be decomposed into a sum of even plus odd
functions.
From these properties, Equation 9.24 and the Fourier coefficient equa-
tions, it follows that, when y(t) is an even periodic function, B
n
= 0 and
y(t) has the Fourier series
y(t) =
A
0
2
+
∞
X
n=1
A
n
cos
2πnt
T
. (9.30)
This is called the Fourier cosine series. Further, when y(t) is an odd
periodic function, A
0
= A
n
= 0 and y(t) has the Fourier series
y(t) =
∞
X
n=1
B
n
sin
2πnt
T
. (9.31)
This is called the Fourier sine series.
Example Problem 9.3
Statement: Find the frequency spectrum of the step function
y(t) =
−A −π ≤ t < 0
+A 0 ≤ t < π
Solution: This is an odd function, therefore A
0
= A
n
= 0.
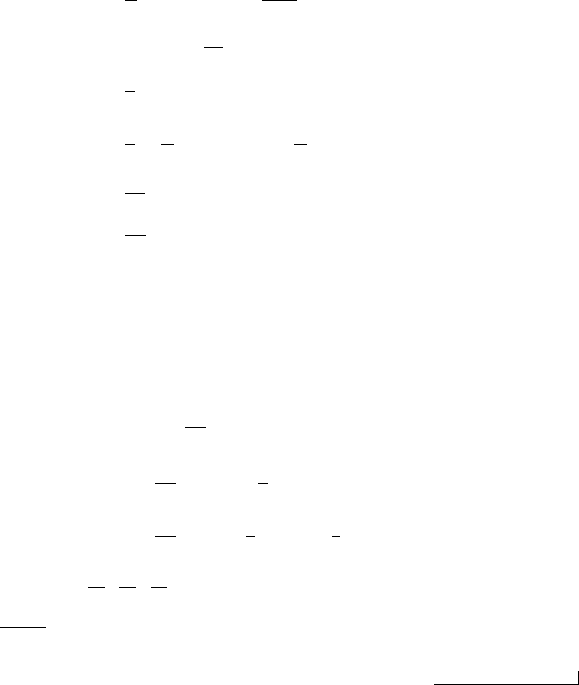
358 Measurement and Data Analysis for Engineering and Science
B
n
=
2
T
Z
T /2
−T /2
y(t) sin
2πnt
T
dt
note : ω =
2π
T
where T = 2π
=
1
π
Z
0
−π
(−A) sin(nt)dt +
Z
π
0
(A) sin(nt)dt
=
1
π
"
A
n
cos(nt)
0
−π
−
A
n
cos(nt)
π
0
#
=
A
nπ
{1 − cos(−nπ) − cos(nπ) + 1}
=
2A
nπ
[1 − cos(nπ)]
= 4A/nπ for n odd
= 0 for n even.
Note that B
n
involves only n and constants.
⇒ y(t) =
∞
X
n=1
B
n
sin(nt)
=
∞
X
n=1
2A
nπ
[1 − cos(nπ)] sin(nt)
=
4A
π
∞
X
n=1,3,5,...
[
1
n
] sin(2πnf t)
=
4A
π
[sin(t) +
1
3
sin(3t) +
1
5
sin(5t) + ...].
y(t) involves both n and t. The frequencies of each of the sine terms are 1, 3, 5, ..., in
units of ω (rad/s), or
1
2π
,
3
2π
,
5
2π
, ..., in units of f (cycles/s = Hz). Generally, this can
be written as f
n
= (2n −1)f
1
. Likewise the corresponding amplitudes can be expressed
as A
n
=
A
1
(2n−1)
, where A
1
= 4A/π. y(t) is shown in Figure 9.10 for three different
partial sums for A = 5.
The contributions of each of the harmonics to the amplitude of the square
wave are illustrated in Figure 9.9. The square wave shown along the back
plane is the sum of the first 500 harmonics. Only the first five harmonics
are given in the figure. The decreasing amplitude and increasing frequency
contributions of the next higher harmonic tend to fill in the contributions of
the previously summed harmonics such that the resulting wave approaches
a square wave.
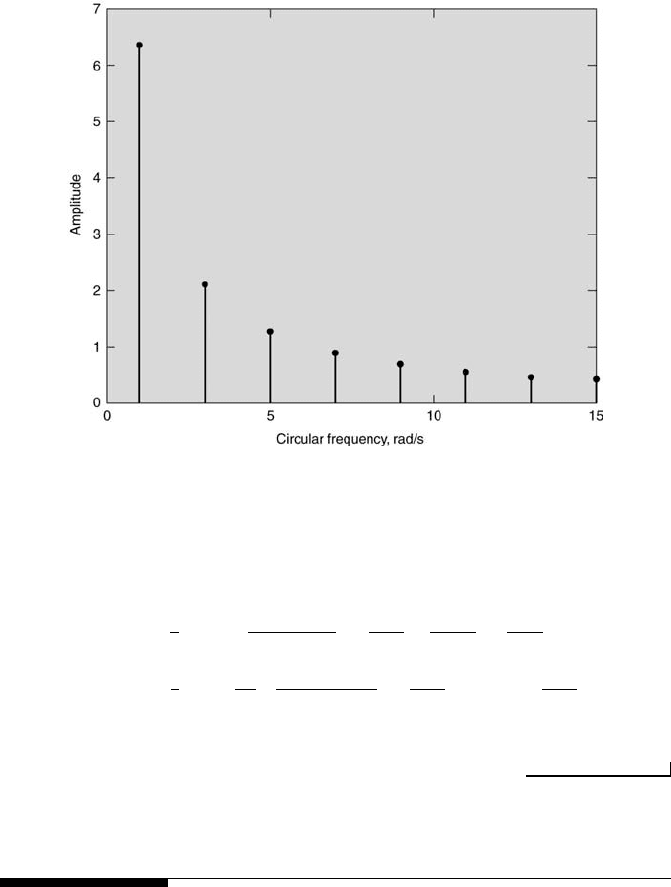
The partial Fourier series sums of the step function are shown in Fig-
ure 9.10 for N = 1, 10, and 500. Clearly, the more terms that are included
in the sum, the closer the sum approximates the actual step function. Rel-
atively small fluctuations at the end of the step can be seen, especially in
the N = 500 sum. This is known as the Gibbs phenomenon. The inclu-
sion of more terms in the sum will attenuate these fluctuations but never
completely eliminate them.
Signal Characteristics 359
FIGURE 9.9
Contributions of the first five harmonics to the Fourier series of a step function.
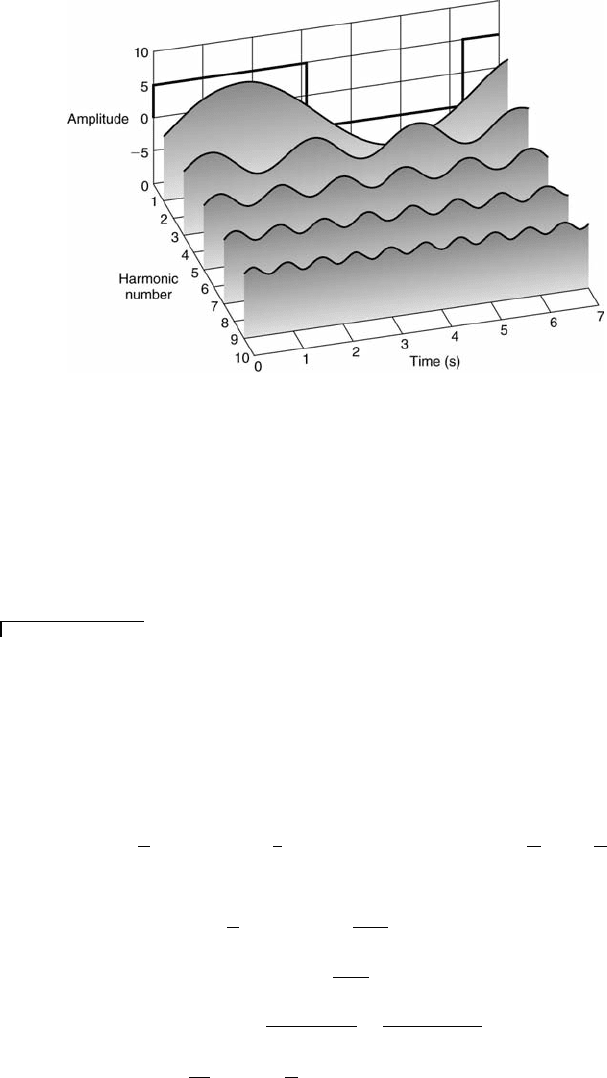
A plot of amplitude versus frequency can be constructed for a square
wave, as presented in Figure 9.11 for the first eight harmonics. This figure
illustrates in another way that the Fourier series representation of a square
wave consists of multiple frequencies of decreasing amplitudes.
Example Problem 9.4
Statement: Find the frequency spectrum of the ramp function:
y(t) =
2At 0 ≤ t < 1/2
0 1/2 ≤ t < 1
with T = 1 s.
Solution: This function is neither even nor odd.
A
0
=
2
T
Z
T /2
−T /2
y(t)dt =
2
1
Z
0
−0.5
0dt +
Z
0.5
0
2Atdt
= 4A
t
2
2
0.5
0
=
A
2
A
n
=
2
T
Z
T /2
−T /2
y(t) cos
2πnt
T
dt
= 2
Z
0.5
0
2At cos
2πnt
T
dt
= 4A
cos(2πnt/T )
(2πn/T )
2
+
t sin(2πnt/T )
(2πn/T )
0.5
0
because
R
t cos mtdt =
1
m
2
cos mt +
t
m
sin mt (from integration by parts). Continuing,

360 Measurement and Data Analysis for Engineering and Science
FIGURE 9.10
Partial Fourier series sums for the step function.
A
n
= 4A
cos nπ − cos 0
(2πn/T )
2
+
0.5 sin nπ − 0
(2πn/T )
= (4A)
T
2
4π
2
n
2
(cos nπ − 1) =
A
π
2
n
2
(cos nπ − 1).
Further,
B
n
=
2
T
Z
T /2
−T /2
y(t) sin
2πnt
T
dt
= 2
Z
0.5
0
2At sin
2πnt
T
dt
= 4A
sin(2πnt/T )
(2πn/T )
2
−
t cos(2πnt/T )
(2πn/T )
0.5
0
because
R
t sin mtdt =
1
m
2
sin mt −
t
m
cos mt (from integration by parts).
So,
B
n
= 4A
sin nπ − sin 0
(2πn/T )
2
+
0.5 cos nπ − 0
(2πn/T )
= (4A)
−0.5 cos nπ
(2πn/T )
=
−A
πn
cos nπ.
Signal Characteristics 361
FIGURE 9.11
Amplitude spectrum for the first eight terms of the step function.
Thus,
y(t) = A
1
4
+
∞
X
n=1
(cos nπ − 1)
π
2
n
2
cos
2πnt
T
−
cos nπ
πn
sin
2πnt
T
!
= A
1
4
+
∞
X
n=1
1
nπ
(−1 + (−1)
n
)
πn
cos
2πnt
T
− (−1)
n
sin
2πnt
T
!
.
This y(t) is shown (with A = 1) for three different partial sums in Figure 9.12.
9.6 Complex Numbers and Waves
Complex numbers can be used to simplify waveform notation. Waves, such
as electromagnetic waves that are all around us, also can be expressed using
complex notation.
The complex exponential function is defined as
exp(z) = e
z
= e
(x+iy)
= e
x
e
iy
≡ e
x
(cos y + i sin y), (9.32)
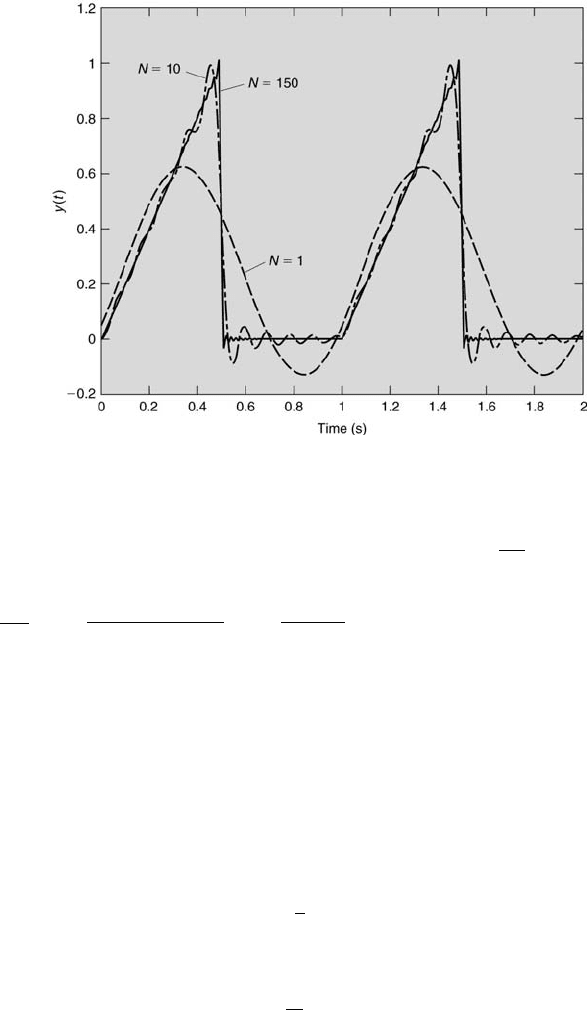
362 Measurement and Data Analysis for Engineering and Science
FIGURE 9.12
Three partial Fourier series sums for a ramp function.
where z = x + iy, with the complex number i ≡
√
−1 and x and
y as real numbers. The complex conjugate of z, denoted by z
∗
, is
z
∗
= x − iy. The modulus or absolute value of z is given by |z| =
√
zz
∗
=
p
(x + iy)(x − iy) =
p
x
2
+ y
2
, which is a real number. Using
Equation 9.32, the Euler formula results,
e
iθ
= cos θ + i sin θ, (9.33)
which also leads to
e
−iθ
= cos θ − i sin θ. (9.34)
The complex expressions for the sine and cosine functions can be found from
Equations 9.33 and 9.34,
cos θ =
1
2
e
iθ
+ e
−iθ
(9.35)
and
sin θ =
1
2i
e
iθ
− e
−iθ
. (9.36)
A wave can be represented by sine and cosine functions. Such represen-
tations are advantageous because [1] these functions are periodic, like many
Signal Characteristics 363
waves in nature, [2] linear math operations on them, such as integration and
differentiation, yield waveforms of the same frequency but different ampli-
tude and phase, and [3] they form complex waveforms that can be expressed
in terms of Fourier series.
A wave can be represented by the general expression
y(t) = A
r
cos
2π
λ
(x − ct) + iA
i
sin
2π
λ
(x − ct), (9.37)
in which A
r
is the real amplitude, A
i
the imaginary amplitude, x the dis-
tance, λ the wavelength, and c the wave speed. This expression can be
written in another form, as
y(t) = A
r
cos(κx − ωt) + iA
i
sin(κx − ωt), (9.38)
in which κ is the (angular) wave number and ω the circular frequency. The
wave number denotes the number of waves in 2π units of length, where
κ = 2π/λ. The wave speed is related to the wave number by c = ω/κ.
The cosine term represents the real part of the wave and the sine term the
imaginary part. Further, the phase lag is defined as
α = tan
−1
(A
i
/A
r
). (9.39)
Equations 9.38 and 9.39 imply that
y(t) =
q
A
2
r
+ A
2
i
cos(κx − ωt − α), (9.40)
in which the complex part of the wave manifests itself as a phase lag.
Example Problem 9.5
Statement: Determine the phase lag of the wave given by z(t) = 20e
i(4x−3t)
.
Solution: The given wave equation, when expanded using Euler’s formula, reveals
that both the real and imaginary amplitudes equal 20. Thus, according to Equation
9.39, α = tan
−1
(20/20) = π/4 radians.
9.7 Exponential Fourier Series
The trigonometric Fourier series can be simplified using complex number
notation. Starting with the trigonometric Fourier series
y(t) =
A
0
2
+
∞
X
n=1
A
n
cos
2πnt
T
+ B
n
sin
2πnt
T
(9.41)
364 Measurement and Data Analysis for Engineering and Science
and substituting Equations 9.35 and 9.36 into Equation 9.41 yields
y(t) =
A
0
2
+
∞
X
n=1
A
n
2
e
inω
0
t
+ e
−inω
0
t
+
B
n
2i
e
inω
0
t
− e
−inω
0
t
, (9.42)
where θ = nω
0
t = 2πnt/T . Rearranging the terms in this equation gives
y(t) =
A
0
2
+
∞
X
n=1
e
inω
0
t
A
n
2
−
iB
n
2
+ e
−inω
0
t
A
n
2
+
iB
n
2
, (9.43)
noting 1/i = −i.
Using the definitions
C
n
≡
A
n
2
−
iB
n
2
(9.44)
and
C
−n
≡
A
n
2
+
iB
n
2
, (9.45)
this equation can be simplified as follows:
y(t) =
A
0
2
+
∞
X
n=1
C
n
e
inω
0
t
+ C
−n
e
−inω
0
t
=
A
0
2
+
−1
X
n=−∞
C
n
e
inω
0
t
+
∞
X
n=1
C
n
e
inω
0
t
. (9.46)
(9.47)
Combining the two summations yields
y(t) =
∞
X
n=−∞
C
n
e
inω
0
t
, (9.48)
where C
0
= A
0
/2.
The coefficients C
n
can be found by multiplying the above equation by
e
−inω
0
t
and then integrating from 0 to T . The integral of the right side
equals zero except where m = n, which then yields the integral equal to T .
Thus,
C
m
=
1
T
Z
T
0
y(t)e
−imω
0
t
dt. (9.49)
What has been done here is noteworthy. An expression (Equation 9.41)
involving two coefficients, A
n
and B
n
with sums from n = 1 to n = ∞,
was reduced to a simpler form having one coefficient, C
n
, with a sum from
n = −∞ to n = ∞ (Equation 9.48). This illustrates the power of complex
notation.
Signal Characteristics 365
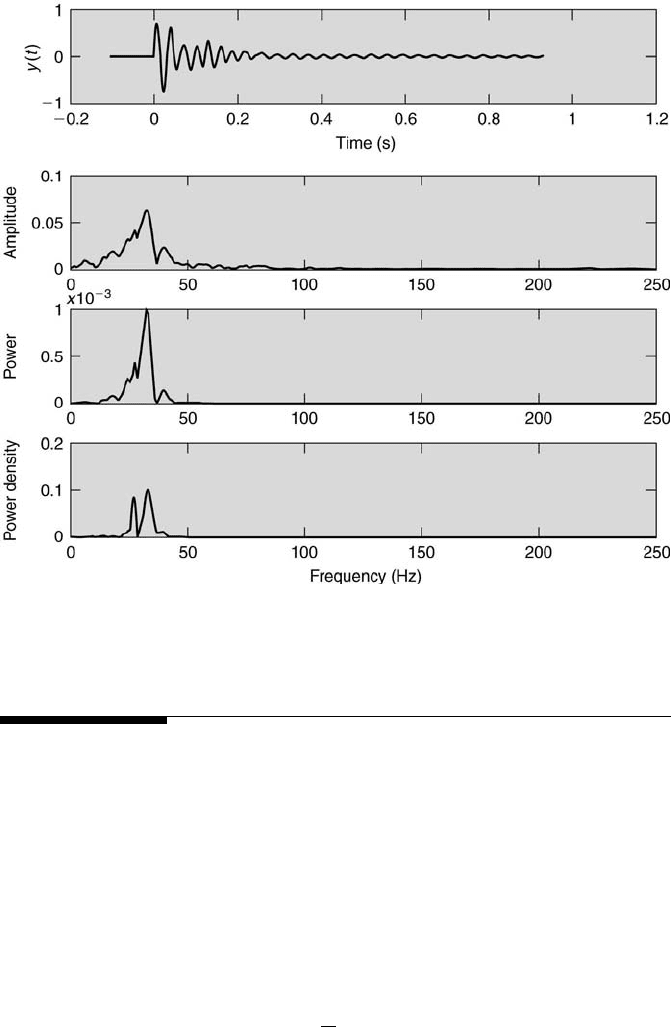
FIGURE 9.13
A signal and its spectra.
9.8 Spectral Representations
Additional information about the process represented by a signal can be
gathered by displaying the signal’s amplitude components versus their cor-
responding frequency components. This results in representations of the
signal’s amplitude, power, and power density versus frequency, which are
termed the amplitude spectrum, power spectrum, and power den-
sity spectrum, respectively. These spectra can be determined from the
Fourier series of the signal.
Consider the time average of the square of y(t),
[y(t)]
2
≡
1
T
Z
T
0
[y(t)]
2
dt. (9.50)
The square of y(t) in terms of the Fourier complex exponential sums is
