Підручник - Алгебра і початок аналізу 10 клас Нелін Академічний рівень
Подождите немного. Документ загружается.

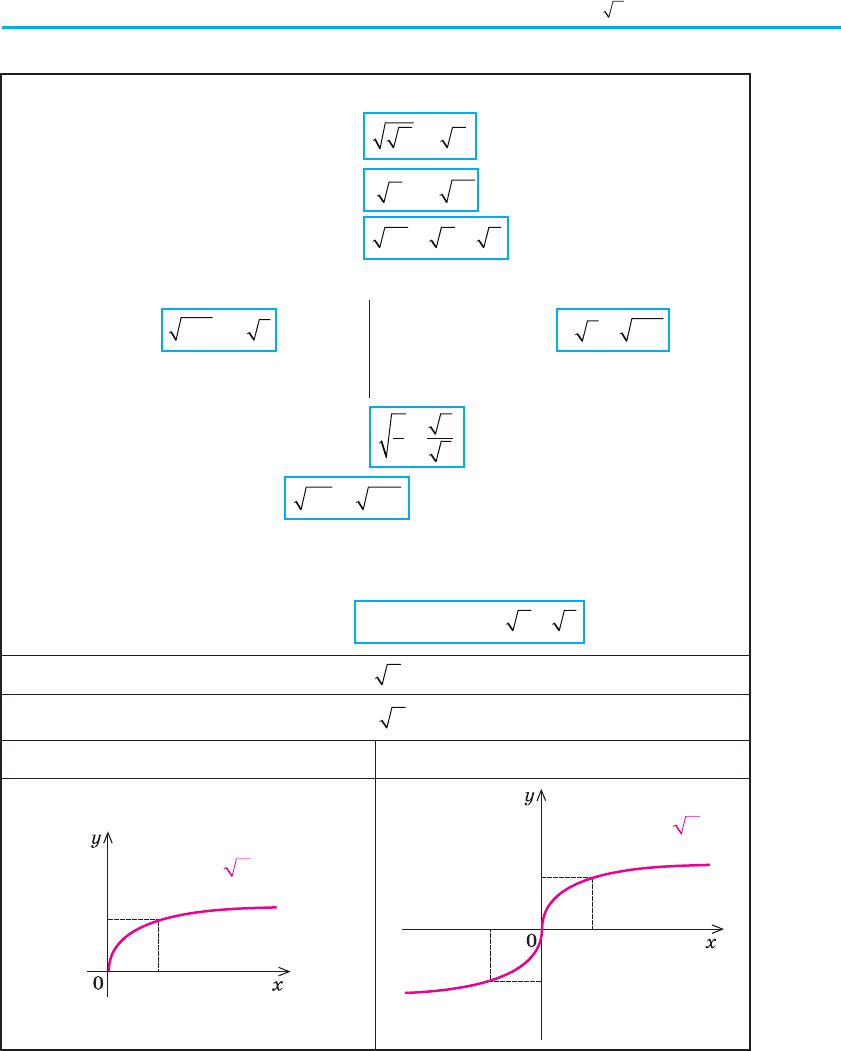
§ 10. Корінь n-го степеня та його властивості. Функція
yx
n
= та її графік 161
Продовження табл. 17
Для довільних значень п і k (n ∈ N, n ≠ 1, k ∈ N)
3) При а l 0
aa
k
n
nk
=
4) При а l 0
aa
n
k
k
n
()
=
5) При а l 0, b l 0
ab
ab
nnn
= æ
Наслідки
При а l 0, b l 0
ab
ab
n
n
n
=
— вине-
сення множника з-під знака кореня.
При а l 0, b l 0
ab
ab
n
n
n
=
— вне-
сення множника під знак кореня.
6) При а l 0, b > 0
a
b
a
b
n
n
n
=
7) При а l 0
aa
m
n
mk
nk
=
— основна властивість кореня
Значення кореня з степеня невід’ємного числа не зміниться, якщо по-
казник кореня і показник степеня підкореневого виразу помножити (або
поділити) на одне й те саме натуральне число.
8) При a l 0, b l 0,
якщо тоab
ab
nn
>>
,
4. Функція
yx
n
= та її графік
Графік функції
yx
n
= (n ∈ N, n l 2)
n — парне (n = 2k, k ∈ N) n — непарне (n = 2k +1, k ∈ N)
1
1
2k
y x=
–1
–1
1
1
2k+1
y
x=
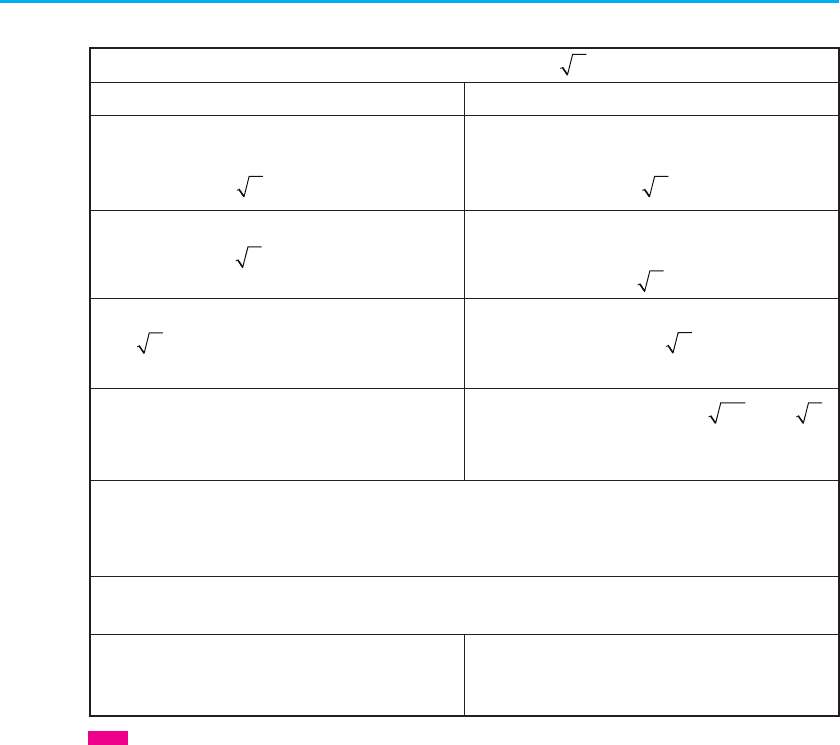
162 Розділ 2. СТЕПЕНЕВА ФУНКЦІЯ
Продовження табл. 17
Властивості функції
yx
n
=
n — парне (n = 2k, k ∈ N) n — непарне (n = 2k +1, k ∈ N)
1. Область визначення: x l 0, тоб-
то
Dx
k2
0
()
=+∞[; ).
1. Область визначення: x ∈ R (x —
будь-яке дійсне число), тобто
Dx
k21+
()
= R.
2. Область значень: у l 0, тобто
Ex
k2
0
()
=+∞[; ).
2. Область значень: у ∈ R (у — будь-
яке дійсне число ), тобто
Ex
k21+
()
= R.
3. Найбільшого значення функція
yx
k
=
2
не має; найменше значення —
у = 0 (при х = 0).
3. Найбіль�ого і наймен�ого зна- Найбіль�ого і наймен�ого зна-Найбіль�ого і наймен�ого зна-
чень функція
yx
k
=
+21
не має.
4. Функція ні парна, ні непарна.
4. Функція непарна: −=−
++
xx
kk
21 21
,
отже, графік функції симетричний
відносно початку координат.
5. Точки перетину з осями координат: Оy
x
y
=
=
0
0
,
;
Оx
y
x
=
=
0
0
,
.
Графік проходить через початок координат.
6. Проміжки зростання і спадання: на всій області визначення функція
зростає.
7. Проміжки знакосталості:
при х > 0 значення у > 0
7. Проміжки знакосталості:
при х > 0 значення у > 0,
при х < 0 значення у < 0
Пояснення й обґрунтування
1. Означення кореня п-го степеня. Поняття кореня квадратного з чис-
ла а вам відомо: це таке число, квадрат якого дорівнює а. Аналогічно
означають і корінь п-го степеня з числа а, де п — довільне натуральне
число, біль�е за 1.
Коренем п-го степеня з числа а називається таке число, п-й степінь
якого дорівнює а.
Наприклад, корінь третього степеня з числа 27 дорівнює 3, оскіль-
ки 3
3
= 27; корінь третього степеня з числа –27 дорівнює –3, оскільки
(–3)
3
= –27. Числа 2 і –2 є коренями четвертого степеня з 16, оскільки
2
4
= 16 і (–2)
4
= 16.
При п = 2 та при п = 3 корені п-го степеня називають також відпо-
відно квадратним та кубічним коренями.
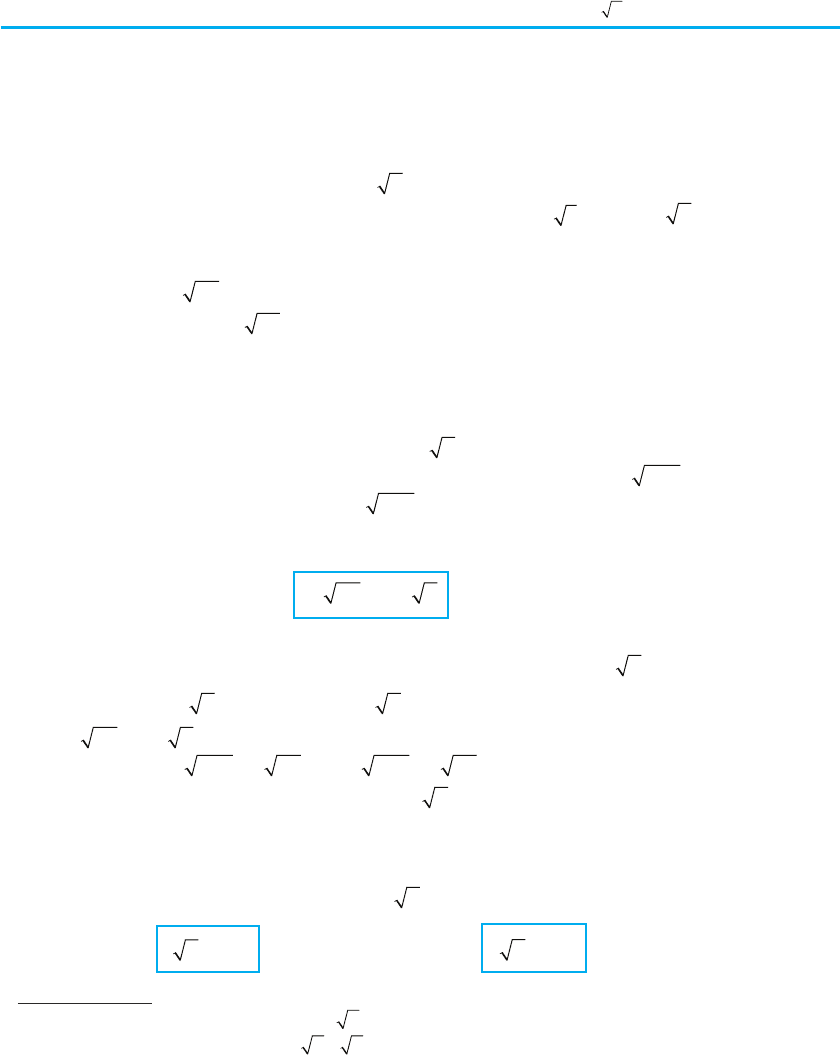
§ 10. Корінь n-го степеня та його властивості. Функція
yx
n
= та її графік 163
Як і для квадратного кореня, для кореня п-го степеня вводять по-
няття арифметичного кореня.
Арифметичним коренем п-го степеня з числа а називається
невід’ємне число, п-й степінь якого дорівнює а.
При а l 0 для арифметичного значення кореня п-го степеня з чис-
ла а існує спеціальне позначення
1
:
a
n
; число n називають показником
кореня, а саме число a — підкореневим виразом. Знак
n
і вираз a
n
на-
зивають також радикалом.
Наприклад, те, що корінь третього степеня з числа 27 дорівнює 3,
записують так:
27 3
3
= ; те, що корінь четвертого степеня із 16 дорів-
нює 2, записують так:
16 2
4
= . Але для запису того, що корінь четверто-
го степеня із 16 дорівнює –2, позначення немає.
При а < 0 значення кореня п-го степеня з числа а існує тільки при
непарних значеннях п (оскільки не існує такого дійсного числа, парний
степінь якого буде від’ємним числом). У цьому випадку корінь непарно-
го степеня п із числа а теж позначають
a
n
.
Наприклад, те, що корінь
третього степеня з числа –27 дорівнює –3, записують так: −=−27 3
3
.
Оскільки –3 — від’ємне число, то
−27
3
не є арифметичним значенням
кореня. Але корінь непарного степеня з від’ємного числа можна вирази-
ти через арифметичне значення кореня за допомогою формули
−=−
++
aa
kk
21 21
.
Щоб довести наведену формулу, зауважимо, що за означенням коре-
ня п-го степеня ця рівність буде правильною, якщо
−
()
=−
+
+
aa
k
k
21
21
.
Дійсно,
−
()
=−
(
)
()
=−
+
+
+
+
+
aa
a
k
k
k
k
k
21
21
21
21
21
1
i
,
а це й означає, що
−=−
++
aa
kk
21 21
.
Наприклад,
−=
−=
−27 27 3
33
;
−=
−=
−32 32 2
55
.
Зазначимо також, що значення a
k21+
має той самий знак, що
й число a, оскільки при піднесенні до непарного степеня знак числа не
змінюється.
Також за означенням кореня п-го степеня можна записати, що
в тому випадку, коли існує значення
a
n
, виконується рівність
aa
n
n
()
=
і, зокрема, при a l 0
aa
()
=
2
.
1
Усі властивості виразів виду a
n
наведено для випадку n ∈ N, n l 2. При
п = 1 домовимося вважати, що
aaa
n
==
1
.
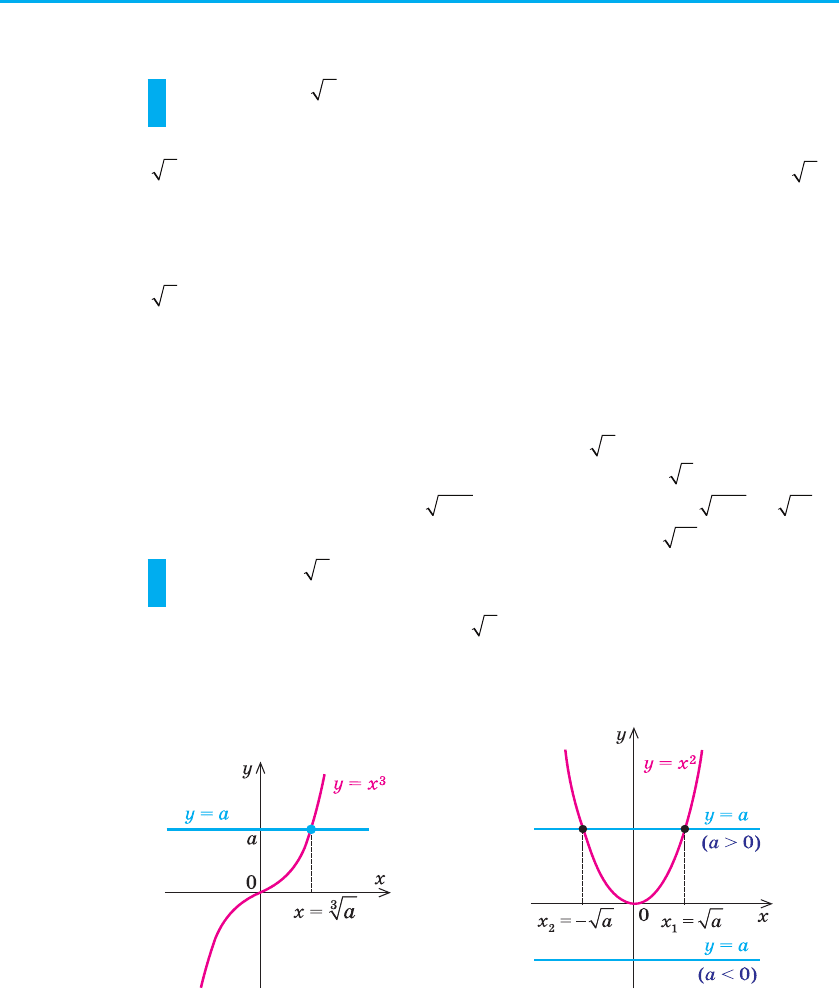
164 Розділ 2. СТЕПЕНЕВА ФУНКЦІЯ
2. Область допустимих значень виразів із коренями n-го степеня.
Розв’язки рівняння x
n
= a (n ∈ N). Зазначимо, що
значення a
k21+
— кореня непарного степеня з числа а — існує
при будь-яких значеннях а.
Обґрунтуємо це, наприклад, для кореня третього степеня. Позначимо
ax
3
= . Тоді за означенням кореня п-го степеня x
3
= a і значення
a
3
буде існувати, якщо рівняння x
3
= a матиме розв’язок.
Зобразив�и графіки функцій y = x
3
і y = a (рис. 78), бачимо, що при
будь-яких значеннях a пряма y = a перетинає графік функції y = x
3
в одній точці. Отже, при будь-якому значенні a існує єдине значення
a
3
(оскільки функція y = x
3
зростає і набуває всіх значень від –∞ до
+∞).
Аналогічне обґрунтування можна навести і для ін�их коренів непар-
ного степеня (див. графіки і властивості функцій виду y = x
2k + 1
у § 12).
Наведені міркування дозволяють записати розв’язки рівняння
х
n
= а для непарних значень п = 2k + 1: при будь-яких значеннях а рів-
няння x
2k + 1
= a (k ∈ N) має єдиний корінь
xa
k
=
+21
.
Наприклад, рівняння х
5
= 3 має єдиний корінь
x = 3
5
, а рівняння
х
7
= –11 має єдиний корінь x =−11
7
(ураховуючи, що
x =− =−11 11
77
,
корінь для рівняння х
7
= –11 можна записати так: x =−
)
11
7
.
Значення a
k2
— кореня парного степеня з числа а — існує
тільки при а l 0.
Дійсно, у тому випадку, коли
ax
k2
= , за означенням кореня п-го
степеня a = x
2k
. Отже, а l 0.
Для квадратного кореня це можна також обґрунтувати, використо-
вуючи відомий графік функції y = x
2
.
Рис. 78 Рис. 79

§ 10. Корінь n-го степеня та його властивості. Функція
yx
n
= та її графік 165
Нехай
ax
= , тоді за означенням квадратного кореня x
2
= a і зна-
чення a буде існувати, якщо рівняння x
2
= a матиме розв’язок.
Зобразив�и графіки функцій y = x
2
і y = a (рис. 79), бачимо, що
пряма y = a перетинає графік функції y = x
2
тільки при a l 0 (при-
чому при a > 0 — у двох точках:
xa
1
= і
xa
2
=− , а при
a = 0 — тільки в одній точці x = 0). Отже, при будь-яких значеннях
a l 0 існує значення a, оскільки функція y = x
2
набуває всіх зна-
чень із проміжку [0; +∞).
Розглянемо розв’язки рівняння x
n
= a для парних значень n = 2k
(k ∈ N).
Рівняння x
2
= a при a < 0 не має коренів, оскільки квадрат будь-
якого числа не може бути від’ємним (на рисунку 79 пряма у = а при a < 0
не перетинає графік функції у = х
2
). Так само рівняння x
2k
= a (k ∈ N)
при a < 0 не має коренів (оскільки парний степінь будь-якого числа не
може бути від’ємним).
При a = 0 рівняння x
2k
= 0 (k ∈ N) має єдиний корінь x = 0 (оскільки
парний степінь будь-якого відмінного від нуля числа — число додатне,
тобто не рівне нулю, а 0
2k
= 0).
При a > 0 за означенням кореня 2k-го степеня
aa
k
k
2
2
()
= . Отже,
xa
k
=
2
— корінь рівняння x
2k
= a. Але −
()
=
()
=
aa
a
k
k
k
k
2
2
2
2
, тому
xa
k
=−
2
—
теж корінь рівняння x
2k
= a. Ін�их коренів це рівняння не має, оскільки
властивості функції y = x
2k
аналогічні властивостям функції y = x
2
: при
x l 0 функція зростає, отже, значення a вона може набувати тільки при
одному значенні аргументу
xa
k
=
()
2
. Аналогічно при x m 0 функція
y = x
2k
спадає, тому значення a вона може набувати тільки при одному
значенні аргументу
xa
k
=−
()
2
. Таким чином, рівняння x
2k
= a при a > 0
має тільки два корені:
xa
k
=±
2
.
Наприклад, рівняння x
10
= –1 не має коренів, а рівняння x
6
= 5 має
корені x =± 5
6
.
3. Властивості кореня п-го степеня можна обґрунтувати, спираючись
на означення кореня n-го степеня.
1) Формула
−=−
++
aa
kk
21 21
була обґрунтована в пункті 1 пояснень.
Обґрунтуємо ін�і формули, наведені в таблиці 17.
Нагадаємо, що за означенням кореня п-го степеня для доведення
рівності
AB
n
= (при A l 0, B l 0) достатньо перевірити рівність
В
n
= А.
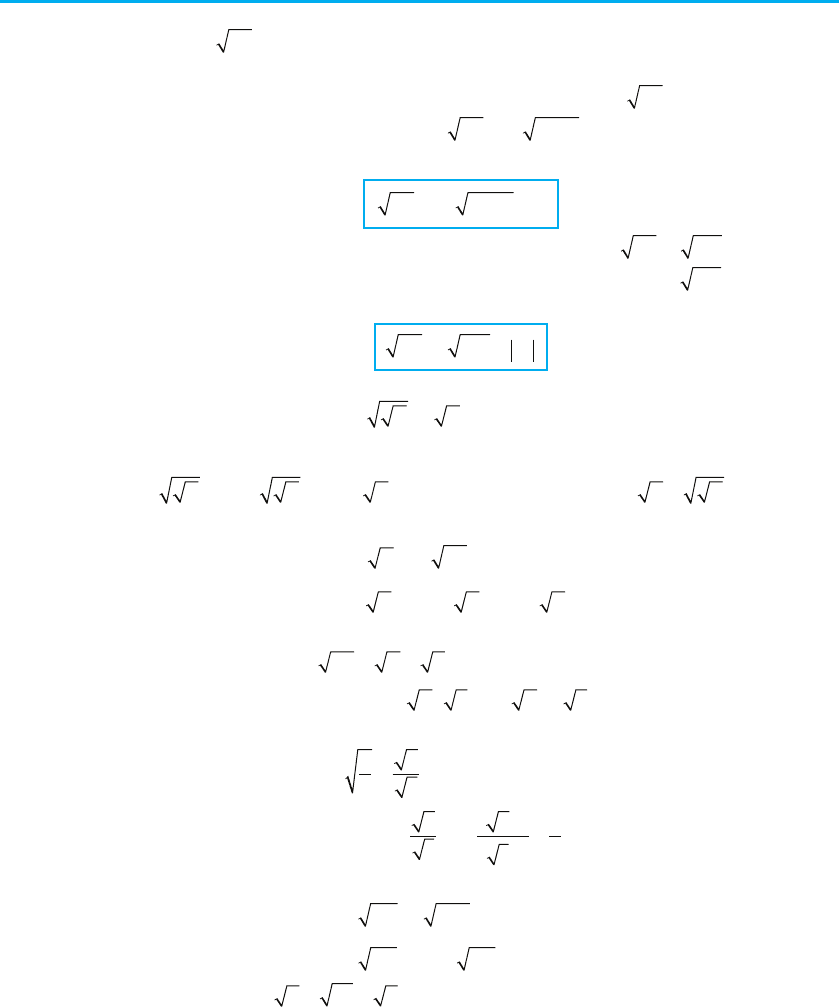
166 Розділ 2. СТЕПЕНЕВА ФУНКЦІЯ
2) Вираз a
n
n
розглянемо окремо при п = 2k + 1 (непарне) і при п = 2k
(парне).
Якщо п — непарне, то враховуємо те, що вираз a
n
n
існує при будь-
яких значеннях а і що знак
aa
n
n
k
k
=
+
+
21
21
збігається зі знаком а.
Тоді за означенням кореня n-го степеня одержуємо
aaa
n
n
k
k
==
+
+
21
21
.
Якщо п — парне, то враховуємо те, що вираз
aa
n
n
k
k
=
2
2
позначає
арифметичне значення кореня n-го степеня (отже,
a
k
k
2
2
0l )
і що
| a |
2k
= a
2k
. Тоді
aaa
n
n
k
k
==
2
2
.
3) Формулу
aa
k
n
nk
= при а l 0
обґрунтуємо, розглядаючи її справа наліво. Оскільки
aa
aa
k
n
nk
k
n
n
k
k
k
()
=
()
()
=
()
= , то за означенням
aa
nk k
n
= .
4) Справедливість формули
aa
n
k
k
n
()
= при а l 0
випливає з рівності aa
aa
n
k
n
n
kn
n
n
k
k
()
()
=
()
=
()
()
= .
5) Для обґрунтування формули
ab
ab
nnn
= æ
при а l 0, b l 0
використовуємо рівність
ab abab
nn
n
n
n
n
n
i
(
)
=
()()
= .
6) Для обґрунтування формули
a
b
a
b
n
n
n
= при а l 0, b > 0
використовуємо рівність
a
b
a
b
a
b
n
n
n
n
n
n
n
=
()
()
= .
7) Властивість кореня
aa
m
n
mk
nk
=
при а l 0
випливає з рівності aa
aa
m
n
nk
m
n
n
k
m
k
mk
()
=
()
()
=
()
= .
Наприклад, 82 2
6
3
6
==
(показник кореня і показник степеня під-
кореневого виразу поділили на натуральне число 3).
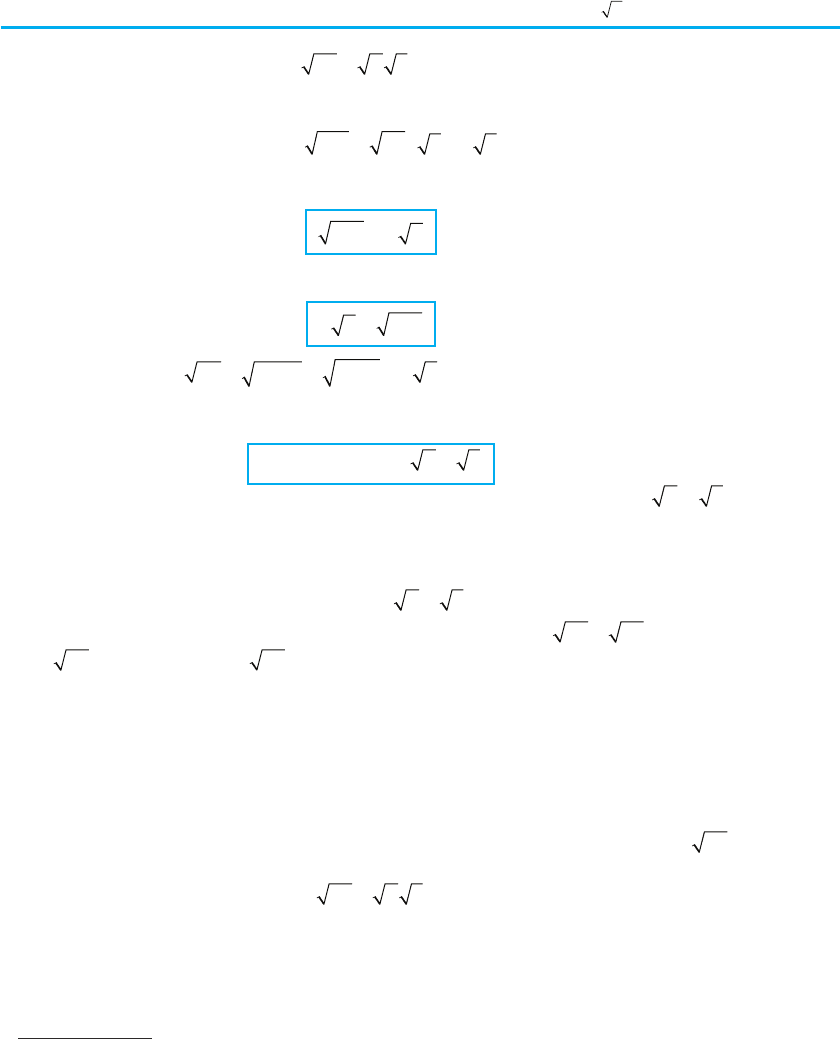
§ 10. Корінь n-го степеня та його властивості. Функція
yx
n
= та її графік 167
За допомогою формули ab
ab
nn
n
= (а l 0, b l 0) можна одержати
важливі наслідки: формули винесення множника з-під знака кореня або
внесення множника під знак кореня.
Дійсно, при а l 0, b l 0 ab abab
n
n
n
n
nn
==
i
. Розглядаючи одержа-
ну формулу зліва направо, маємо формулу винесення невід’ємного множ-
ника з-під знака кореня:
ab
ab
n
n
n
=
,
а справа наліво — формулу внесення невід’ємного множника під знак
кореня:
ab ab
n
n
n
=
.
Наприклад, 96 32 32323
5
5
5
5
5
===
ii
.
8) Зазначимо ще одну властивість коренів n-го степеня:
для будь-яких невід’ємних чисел a і b
якщо a > b, то
ab
nn
>
.
Доведемо це методом від супротивного. Припустимо, що
ab
nn
m .
Тоді при піднесенні обох частин останньої нерівності з невід’ємними
членами до n-го степеня (із збереженням знака нерівності) одержу-
ємо правильну нерівність a m b. Це суперечить умові a > b. Отже,
на�е припущення неправильне і
ab
nn
> .
Наприклад, ураховуючи, що 21 > 16, одержуємо 21 16
4
4
> . Оскіль-
ки 16 2
4
= , маємо, що 21 2
4
> .
Узагальнення властивостей кореня n-го степеня
1
Основна частина формул, які виражають властивості коренів n-го
степеня, обґрунтована для невід’ємних значень підкореневих виразів.
Але інколи доводиться виконувати перетворення виразів з коренями
n-го степеня і в тому випадку, коли таких обмежень немає, наприклад
добувати корінь квадратний (або в загальному випадку корінь парного
степеня) з добутку ab від’ємних чисел (a < 0, b < 0). Тоді ab > 0 і ab
k2
існує, проте формулою
ab
ab
nn
n
=
(1)
скористатися не можна: вона обґрунтована тільки для невід’ємних зна-
чень a і b. Але у випадку ab > 0 маємо: ab = | ab | = | a |•| b | і тепер
| a | > 0 та | b | > 0. Отже, для добування кореня з добутку | a |•| b | можна
використати формулу (1).
1
Цей матеріал є обов’язковим тільки для класів фізико-математичного профілю.

168 Розділ 2. СТЕПЕНЕВА ФУНКЦІЯ
Тоді при a < 0, b < 0 можемо записати:
ab ab
ab
k
kk
k
2
222
==
ii
.
Зазначимо, що одержана формула справедлива і при a l 0, b l 0,
оскільки в цьому випадку | a | = a і | b | = b. Отже,
при ab l 0 ab
ab
k
kk
2
22
=
i
.
Аналогічно можна узагальнити властивість 6.
При
a
b
l 0
a
b
a
b
k
k
k
2
2
2
=
Слід зазначити, що в тих випадках, коли обґрунтування основних
формул можна повторити і для від’ємних значень a і b, такими фор-
мулами можна користуватися для будь-яких а і b (з ОДЗ лівої частини
формули).
Наприклад, для коренів непарного степеня для будь-яких значень a і b
ab
ab
kkk21 21 21+++
=
i
.
(2)
Дійсно, ліва і права частини цієї формули існують при будь-яких
значеннях a та b і виконується рівність
ab abab
kk
k
k
k
k
k
21 21
21
21
21
21++
+
+
+
+
()
=
()()
i
2+1
= .
Тоді за означенням кореня (2k + 1)-го степеня виконується і рівність (2).
Наприклад, ab ab
ab
15
3
15
3
3
5
3
==
i
при будь-яких значеннях a і b.
Але деякими формулами не вдається скористатися для довільних
значень a і b. Наприклад, якщо ми за основною властивістю кореня за-
пи�емо, що
aa
2
6
3
= (показник кореня і показник степеня підкоренево-
го виразу поділили на натуральне число 2), то одержана рівність не
є тотожністю, оскільки при a = –1 (ліва і права частини цієї рівності
означені при всіх значеннях a) маємо −
()
=−
11
2
6
3
, тобто 1 = –1 — не-
правильну рівність.
Таким чином, при діленні показника кореня і показника степеня
підкореневого виразу на парне натуральне число потрібно узагальнити
основну властивість кореня. Для цього достатньо помітити, що a
2
= | a |
2
,
і тепер основа степеня підкореневого виразу | a | l 0, а отже, можна ви-
користати основну формулу (властивість 7): aa a
2
6
2
6
3
==
.
У загальному випадку, якщо при використанні основної властивос-
ті кореня доводиться ділити показник кореня і показник степеня під-
кореневого виразу на парне натуральне число, то в результаті основу
степеня підкореневого виразу потрібно брати за модулем, тобто

§ 10. Корінь n-го степеня та його властивості. Функція
yx
n
= та її графік 169
aa
km
kn
m
n
2
2
=
.
Аналогічно можна обґрунтувати й ін�і приклади використання
основних властивостей коренів при довільних значеннях а і b (з ОДЗ
лівої частини формули), які наведено в таблиці 18.
Таблиця 18
Основні формули для
кореня п-го степеня
(тільки для
невід’ємних значень
а і b, тобто
a
b
l
l
0
0
,
Чи можна користуватися основними формулами
для будь-яких а і b з ОДЗ лівої частини
формули (якщо ні — дано узагальнену формулу)
корінь
непарного степеня
корінь
парного степеня
1.
aa
n
n
()
=
можна
тільки для
невід’ємних а
2.
aa
n
n
=
можна
aa
k
k
2
2
=
3. Корінь із кореня
aa
k
n
nk
=
можна можна
4. Корінь із добутку
ab
ab
nn
n
=
можна
ab
ab
k
kk
2
22
=
і добуток коренів
ab ab
nn n
=
можна
5. Корінь із частки
a
b
a
b
n
n
n
= (b ≠ 0)
можна
a
b
a
b
k
k
k
2
2
2
=
і частка коренів
a
b
a
b
n
n
n
=
можна
6. Основна властивість
кореня:
aa
m
n
mk
nk
=
і навпаки
можна, якщо всі
корені непарного сте-
пеня (тобто перехід не-
парний → непарний)
Перехід парний →
парний можна
Перехід непарний →
парний
a
aa
aa
m
n
mk
nk
m
mk
nk
m
=
−<
при
при
l 0
0
,
aa
mk
nk
m
n
=
aa
mk
nk
m
n
=
170 Розділ 2. СТЕПЕНЕВА ФУНКЦІЯ
Продовження табл. 18
Основні формули для
кореня п-го степеня
(тільки для
невід’ємних значень
а і b, тобто
a
b
l
l
0
0
,
Чи можна користуватися основними формулами
для будь-яких а і b з ОДЗ лівої частини
формули (якщо ні — дано узагальнену формулу)
корінь
непарного степеня
корінь
парного степеня
7. Винесення множни-
ка з-під знака кореня
ab
ab
n
n
n
=
можна
ab
ab
n
n
n
=
8. Внесення множника
під знак кореня
ab
ab
n
n
n
=
можна
ab
ab a
ab a
n
n
n
n
n
=
−<
,
,
при
при
l 0
0
,
,
де b l 0
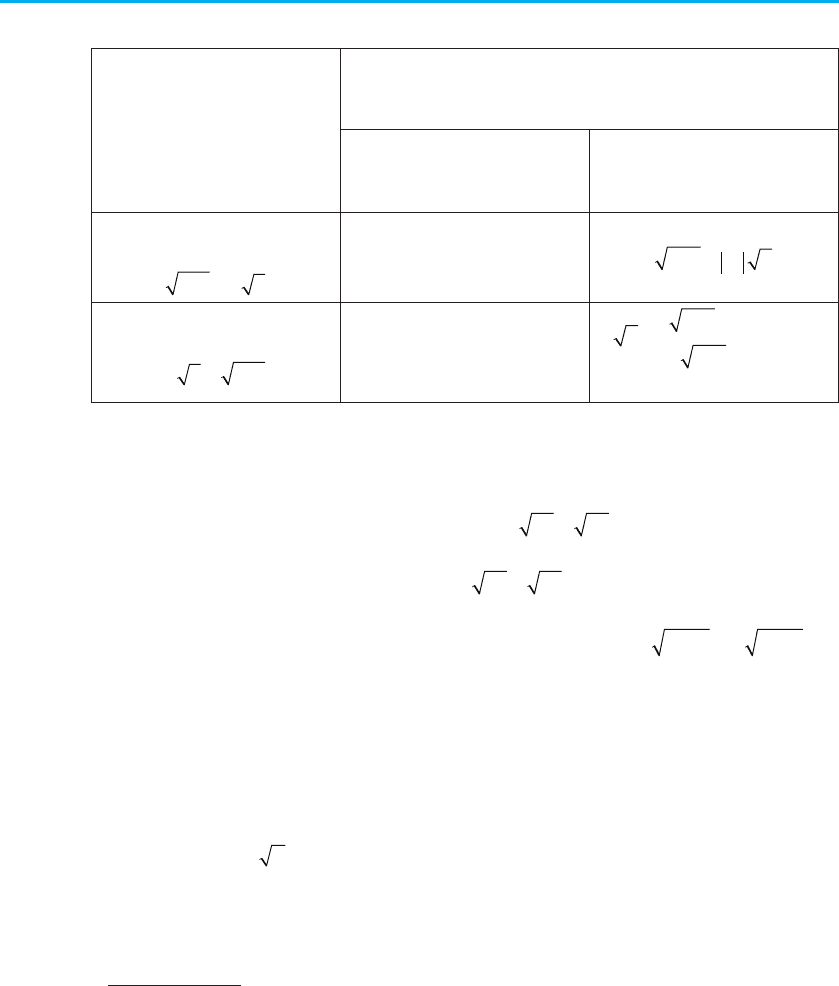
Заува ження. Під терміном «перехід», який використано в табли-
ці 18, слід розуміти перехід у відповідній формулі від кореня п-го степе-
ня до кореня т-го степеня.
Якщо п і т обидва парні, то такий перехід коротко охарактеризова-
но як «перехід парний → парний» (типу
aa
2
4
4
8
=
)
.
Якщо п і т обидва непарні, то в таблиці записано, що виконано «пе-
рехід непарний → непарний» (типу
aa
9
15
3
5
=
)
.
Якщо п — непарне число, а т — парне число, то в таблиці говорить-
ся, що виконано «перехід непарний → парний» (типу
() ().−=−−
)
22
3
5
6
10
Таким чином, якщо за умовою завдання на перетворення виразів
із коренями n-го степеня (ірраціональних виразів) відомо, що всі букви
(які входять до запису заданого виразу) невід’ємні, то для перетворення
цього виразу можна користуватися основними формулами, а якщо та-
кої умови немає, то необхідно аналізувати ОДЗ заданого виразу і тільки
після цього вирі�увати, якими формулами користуватися — основними
чи узагальненими.
4. Функція
yx
n
= (n ∈ N, n l 2) та її графік. Характеризуючи власти-
вості функцій, найчасті�е виділяють такі їх характеристики: 1) область
визначення; 2) область значень; 3) парність чи непарність; 4) точки пере-
тину з осями координат; 5) проміжки знакосталості; 6) проміжки зрос-
тання і спадання
1
; 7) найбіль�е і наймен�е значення функції.
1
Проміжки зростання і спадання функції інколи називають проміжками
монотонності функції.
