Peube J-L. Fundamentals of fluid mechanics and transport phenomena

Подождите немного. Документ загружается.

General Properties of Flows 333

infinity, even if the angle of the planes tends to zero ([SCH 99], p. 104). In these

conditions, the uniqueness of the solution is not assured.

6.6.3.3.

Comparison with experiments and consequences

In practice, flow is possible in a divergent channel, but it is not possible to model

this using an inviscid fluid, even for very large Reynolds number values. A section

of convergent pipe transforms the mechanical power



ppq

 provided by the

pressure difference into an increase in the kinetic energy flow

between

the inflow and outflow sections (section 6.5.2.4). A divergent section leads to the

opposite transformation: kinetic energy is partially recovered in the pressure.

We define the efficiency of these transformations using the kinetic energy flow

between the inflow and outflow sections (section 6.5.2.4) and the

mechanical power



ppq

 provided or recovered by the pressure difference.

Whereas a pipe with a convergent section in the flow direction transforms pressure

into kinetic energy with good efficiency, the inverse effect in a divergent pipe occurs

with a non-negligible dissipation. For a given ratio S

/ S

of the sections S

and S

the efficiency is close to 1 in a converging flow for a short length

whereas in a

divergent pipe, the efficiency goes through a maximum of the order of 0.7-0.8 for an

angle of about 7º. A compromise must be found between a small angle and a large

length over which there exists a notable viscous dissipation, and a larger angle

leading to the formation of a separated flow at the wall, whose kinetic energy is

nearly entirely lost.

The approximation of the flow by slices (uniform velocity distribution in the

stream tube constituted by the pipe) is always a good approximation for steady flow

in a convergent pipe. On the other hand, this approximation is a poor model in a

divergent element, because numerous phenomena can occur which contradict the

assumption of uniform velocity and lead to the loss of mechanical energy (tendency

for the flow to separate close to the wall in the boundary layer (section 6.6.3.7),

instabilities close to the wall leading to the generation of turbulence, etc.).

The experiment always amounts to an observable process, and thus to a well-

posed problem provided a suitable analysis is performed. As we have just seen, the

same is not true for theoretical models for which the initial conditions must be

ascertained by experiment. In particular, methods of numerical solution of the

Navier-Stokes equations often relies on the computation of a velocity field from a

pressure field, which allows, at the next iteration, the computation of a new pressure

field, hence a velocity field and so on. These intermediate fields are not solutions of

the equations of motion, and the intermediate pressure fields can thus correspond to

334 Fundamentals of Fluid Mechanics and Transport Phenomena

initial conditions which lead to a rapid divergence of the velocity field at the

following approximation. This is an important and unfortunately common difficulty.

6.6.3.4.

Separation in unsteady flow

We have seen (section 6.5.3.7) that separation is due to the quadratic term in the

Bernoulli’s theorem for an inviscid fluid. The argument thus invoked is no longer

valid in a strongly unsteady flow. Consider an irrotational unsteady flow for which

we have Bernoulli’s second theorem ([6.13]).

When the dynamic pressure

V is smaller than the term tww

, the

phenomenon of flow separation at the wall no longer occurs. If the flow is

oscillatory, the velocity profile may present changes of sign, but there no longer

generally exists a rear stagnation point S at the origin of a streamline towards the

heart of the fluid (Figure 6.20a), which is characteristic of a 2D separation.

6.6.4. Non-existence of a steady solution

Even if we impose steady conditions at the fluid domain boundaries, we do not

encounter steady flows in very many situations. The wakes observed behind

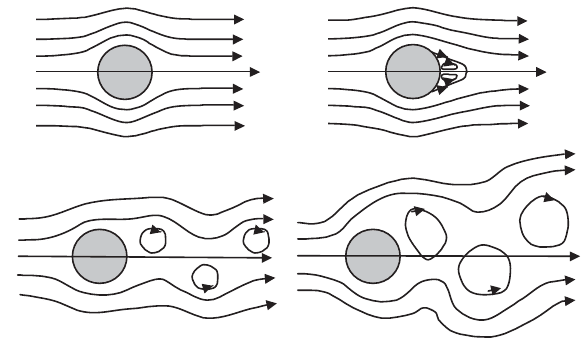
obstacles belong to this category. Let us reconsider the example of a circular

cylinder of diameter D (without circulation) in a velocity field which is assumed to

be uniform and steady at infinity. The structure of the flow depends on the Reynolds

number

UD Re .

General Properties of Flows 335

(a)

(b)

(c)

(d)

Figure 6.23.

Real flow around a circular cylinder placed in a uniform steady velocity field

Figure 6.23 shows the evolution of this flow as the Reynolds number increases.

For values of the Reynolds number small compared to 1, the flow is symmetric

(Figure 6.23a); the dissymmetry between upstream and downstream increases with

the Reynolds number; for larger values (of the order of 0.2-20) we observe the

appearance of a fixed zone of reversed flow just downstream of the cylinder

(attached wake (Figure 6.23b)) comprising two symmetric vortices). For values

greater than 20 (Figure 6.23c), we observe the emission of alternate vortices at a

well-defined frequency. Beyond values of Re of the order of 1,000, the periodicity

of the vortices is attenuated (Figure 6.23c) and random fluctuations appear.

6.6.4.1.

The creation of the circulation

We have studied the flow around a circular cylinder with circulation (section

6.2.5.2.4). The origin of this circulation cannot be explained by a rotation of the

cylinder since the fluid is inviscid. Experiment furthermore shows that an important

difference exists between the circulation calculated in the fluid and the circulation

calculated on the cylinder using the velocity at the wall. This difference shows that

the circulation is not created directly by viscous diffusion from the wall, which is

not significant in an inviscid fluid.

The

circulation is in fact created during the transitional regime

of the flow. It is

due to the viscosity of the fluid. Consider a fluid initially at rest about a profiled

body at incidence. In the initial acceleration regime of the flow around the body, a

dissymmetry appears between the intrados (the under-side) and the extrados (the

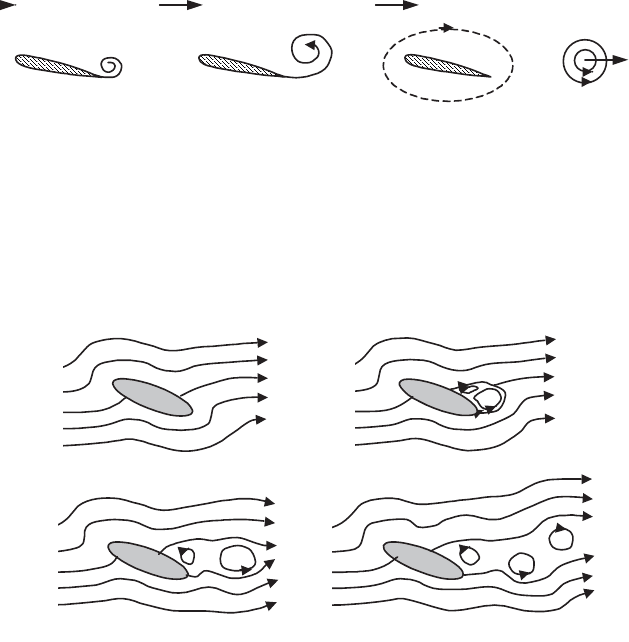
336 Fundamentals of Fluid Mechanics and Transport Phenomena

upper-side) of the profile which generates at the trailing edge (downstream of the

boundary layers) a sheared viscous flow at the origin of a vortex, which grows

(Figure 6.24a and Figure 6.24b) until it separates from the obstacle and is carried

away by the flow (Figure 6.24c). The viscosity is only important for a small zone

and Lagrange’s theorem can be applied in the inviscid fluid external to the ensemble

of the obstacle and the vortex. As the circulation is initially zero, it remains so: the

vortex carries away the circulation

, and the opposite circulation –

is established

about the obstacle.

(a) (b) (c)

U(t)

U(t) U(t)

Figure 6.24.

Creation of circulation by initial emission of a vortex around a profiled body

The circulation about a non-profiled obstacle is created by the same transitional

mechanism, to which is added a turbulent wake analogous to that described in

section 6.6.3.4, and which does not create and additional mean circulation.

(a)

(b)

(c)

(d)

Figure 6.25.

Creation of circulation by initial emission of a vortex

around a non-profiled body: (a) and (b) development of the initial vortex;

General Properties of Flows 337

6.6.4.2.

Instabilities and turbulence

The phenomena described in the preceding sections result from flow instabilities,

in other words to phenomena associated with the amplification of perturbations of

varying amplitudes. Situations of instability are numerous in fluid mechanics and the

viscosity is not necessarily a damping factor for these phenomena. On the other

hand, in so far as the most unstable structures correspond to high Reynolds numbers,

the characteristic time constant of the amplification is much lower than the damping

time.

Instabilities evolve in general towards a variety of more of less complex

situations; for high Reynolds numbers corresponding to the flows encountered in

practice, we see the appearance of random fluctuations the details of which are

unpredictable (chaos). The velocity fluctuations of fluid particles also lead to the

fluctuations of other extensive quantities, and the transfer mechanisms of

irreversible phenomena are significantly changed ([SCH 99], [YIH 77]).

This page intentionally left blank

Chapter 7

Measurement, Representation and

Analysis of Temporal Signals

The measurement of flows and transfer mechanisms presents specific difficulties

related to fluid movement. We will review the principles of the main measurement

methods. A synthesis of the different signal processing procedures commonly used

in the domains studied, and the various numerical techniques used in order to

implement these, will be presented.

7.1. Introduction and position of the problem

The modeling of macroscopic phenomena can be more or less detailed. The

representation of the continuous medium by means of fields of continuous quantities

was obtained by extending systems of finite dimensions in thermodynamic

equilibrium to their limits. Writing an infinite number of values of a continuous

field is obviously impossible and constitutes the infinite limit of a practical

realization; this can only be achieved if we dispose of a procedure for computing the

value at every point, which can be trivial and consist of the simple condition of a

constant value. Furthermore, discrete systems in thermodynamic equilibrium

constitute a more or less good approximation to a real system. The information

necessary for the description of a continuous system always therefore comprises an

ensemble, necessarily finite, of numerical values and a procedure for the

computation of quantities at all points, which amounts to an interpolation.

A material ensemble is described by means of quantities characterized by

measurements which permit the representation of its evolution. The equations are

340 Fundamentals of Fluid Mechanics and Transport Phenomena

exact equalities between real (or complex) numbers, which represent the physical

quantities studied. Now, these are never known exactly and this exact knowledge is

furthermore neither practically obtainable nor necessary. We work with

approximations or mathematical representations (transformed signals) which are

more convenient to use. The values themselves can be synthesized by a

transformation procedure allowing their number to be reduced. The representation

of physical quantities is thus a basic problem associated with our knowledge of the

phenomena of interest. These considerations can apply both to space and time

variant quantities. In what follows we will reason in terms of a temporal

representation of a signal, but the problems discussed are analogous regardless of

the nature of the representation and the number of variables.

Time is a particular variable, since the cause of a phenomenon observed at time

can only be a function of the state variables from earlier times: only the past

influences the future. In reality, this property is also encountered for spatial

variables in flows, since the extensive properties remain attached to the matter in

movement. The notion of causality, largely developed in signal processing can in

fact by applied in space-time over characteristic curves or the succession of

characteristic surfaces. While causality appears obvious for the time-direction

considered in isolation, the problem is far less simple when we perform a Fourier

transform. We will not cover problems of causality which appear in integral

transformations: the reader should refer to the specialized literature ([AND 99],

[BEE 03], [DEB 06], [PRE 91]).

The idea of continuous phenomena has only really been used by some modern

calculation methods. The first analog calculators produced a physical representation

of the equations, the adjustment of the variables and parameters being achieved by

modification of physical quantities (for example, voltage for electronic calculators

or pressure for hydraulic and pneumatic systems). With numerical calculation, we

operate using numerical values, which requires equations to be discretized.

7.2. Measurement and experimental data in flows

7.2.1. Introduction

Knowledge of a physical system requires the measurement of its quantities. In

general, the local intensive quantities are easier to measure than the extensive

quantities which are most often measured indirectly using equations of state,

phenomenological laws or relationships obtained theoretically (for example,

Bernoulli’s theorem). As we cannot here provide detailed description of

measurement methods, we will simply indicate the principles on which these are

Measurement, Representation and Analysis of Temporal Signals 341

based. The quantities measured are primarily the pressure, the velocity, the

temperature and the concentration of a constituent.

7.2.2. Measurement of pressure

As pressure is a force normal to a surface, its direct measurement can be related

to the measurement of a force; as the force is the energetic intensive quantity

associated with a displacement in a fixed discrete system, we are dealing with a

measurement of displacement which is in fact achieved by the intermediary of

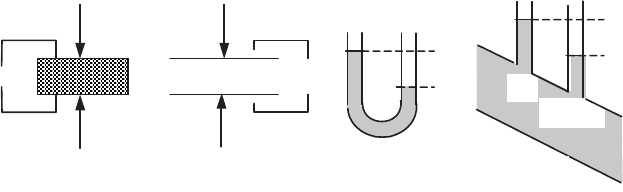
associate electrical or electromagnetic phenomena. Let us consider a few examples

of such measurement devices: piezoresistive probes where deformation of the

silicon membrane produces variations in electrical resistance, capacitive probes

(Figure 7.1b) which comprise a fixed electrode opposite the membrane, the

movement of the latter is accompanied by a variation of the capacitance, or

piezoelectric probes (Figure 7.1a) that comprise a piezoelectric material on which

the action of a force creates a difference of potential.

For steady flow, a measurement which is less and less frequently employed

consists of using liquid manometers, based on hydrostatics laws, to find the

difference in height 'h between the free surfaces in two tubes implying a pressure

difference equal to

U

g'h, or between two free surfaces if the two tubes

communicate directly, or, between the pressure taps in the liquid. We measure here

a difference of level (a length), but the real difficulty comes from the accurate

identification of the position of the free surface and the effects of surface tension

(section 2.2.1.4.2).

+ + + +



e(t)

f(t)

+ + + +



e(t)

f(t)

(a) (b) (c)

(d)

Figure 7.1. Probes for pressure (a), (b) and (c) and driving pressure (d) measurements

The pressure measured by a probe is the surface force on the sensitive member

of the probe. Pressure measurement at a point in a fluid requires in principle that the

probe is positioned such that it does not itself create a perturbation: it must therefore

be carried with the matter in movement. This is clearly unrealistic, unless some

342 Fundamentals of Fluid Mechanics and Transport Phenomena

optical means of pressure measurement could be made – and this is generally not

possible. In practice, it is only possible to use some instrument, which is integrated

into a solid surface. It is thus necessary to extract the pressure and transmit it to the

sensitive surface of the probe by means of a pneumatic or hydraulic link.

The extraction of pressure can be performed by means of an orifice at the tube

extremity used for its transmission. The tube extremity comprises an obstacle in a

flow, and this must be considered. We can assume that the pressure in an orifice

pierced in a wall is the pressure in the fluid at that point. We can in fact consider

that the flow is here parallel to the wall, without any velocity component normal to

the wall; the balance of transverse forces is zero on any fluid element, hence the

local uniformity of pressure along the wall normal. However, the pressure tube must

be contained in a suitable obstacle, such that it does not modify the flow and

therefore the pressure value. We will come back to this point a little later when we

deal with velocity measurements.

Furthermore, the transmission of pressure fluctuations by a tube is a delicate

problem when the length of the tube is more than a few centimeters, as it is

necessary to avoid problems of acoustic resonance [GAB 98]. However, this

problem is beyond the scope of this work.

7.2.3. Anemometric measurements

7.2.3.1. Introduction

On a wall, the velocity of a fluid in motion is equal to that of the wall. It is

obviously only of interest to measure the velocity at points at the heart of the flow.

When making direct measurements of velocity, it is necessary to consider individual

fluid particles, of a given size, and to obtain an electrical or optical signal which

results from a phenomenon associated with the velocity of this fluid particle.

Velocity measurement devices (anemometers) which allow direct measurement are

mainly laser Doppler anemometers, cup anemometers, etc.). Indirect measurement

of velocity can be obtained by means of pressure measurements by application of

the laws of fluid mechanics (Pitot tubes, total pressure probes, etc.) or from

calibrated thermal measurements (hotwire anemometers). The same is true for

measurements of the flow rate, which are not generally made by directly measuring

the volume or mass which flowed during some given time.

As for the pressure, it is necessary to measure the local property of a material

element (Lagrangian measurement) or to introduce a probe which is sensitive to the

local velocity but which will necessarily disturb the flow (Eulerian measurement).