Peube J-L. Fundamentals of fluid mechanics and transport phenomena
Подождите немного. Документ загружается.


General Properties of Flows 303
It is immediately verifiable from place to place that the functions
i
u
~
are variables
of separated functions and that they are proportional to the successive derivatives of
f(t):
¦
f
0
)(
~
)
~
,
~
()
~
,
~
,
~
(
~
i
i
i
tfzygtzyu [6.71]
The functions )
~
,
~
( zyg
i
are solution of the system:
01021 1
1; ; ; ... , ...
nn
ggggggg''' '
with the boundary conditions:
( , ) 0 ( , ) ; 0,1,..., ...
i
gyz yz C i n
The preceding equations can be solved successively with increasing i, and the
first equation corresponds to the Poiseuille flow (section 3.4.2.5). Let
H
= 1, which
amounts to taking
Q
2
DT as a unit of time. The expression for the velocity
becomes:
)
~
,
~
(
~
)
~
,
~
,
~
(
~
,,
0
)(
zygtfUtzyuUtzyu
i
i
i
¦
f
The volume flow rate can thus be easily expressed as a function of the successive
derivatives of the pressure gradient:
sdzygtfUDsdtzyuUDq
S
i
i
i
S
v
~
)
~
,
~
(
~
~
)
~
,
~
,
~
(
~
0
)(22
³
¦
³
f
Defining the dimensionless coefficients sdzygG
S
ii
~
)
~
,
~
(
³
, it can be written in
the form:
¦
f
0
)(2
~
i
i
iv
tfGUDq
Let 'p(t) be the driving pressure loss for the length L; the pressure gradient can
be written in the form:
L
tp
x
p '
w
w
and we have:
¸
¸
¹
·
¨
¨
©
§
'
w
w
¸
¸
¹
·
¨
¨
©
§
L
p
t
D
U
D
tf
i
i
i
i
QP
22
)(
~

304 Fundamentals of Fluid Mechanics and Transport Phenomena
From this we can derive an expression for the volume flow rate as a function of
the pressure loss and its temporal derivatives:
¦
f
¸
¸
¹
·
¨
¨
©
§
'
w
w
¸
¸
¹
·
¨
¨
©
§
0
24
i
i
i
i
iv
L
p
t
D
G
D
q
QP
For example, in the case of a circular cross-section C (
¸
¸
¹
·
¨
¨
©
§
w
w
w
w
'
r
r
rr
~
~
~~
1
~
) of
radius 1r
, we easily find:
4
22
01
6
24
2
113
1; ;
41644
119
3;...
256 9 9
r
gr r gr r
r
gr r r
¬
®
¬
®
The physical interpretation of the series is not so simple, as the physical
significance of the higher order derivatives implies a long-term property. It suffices
to consider a function
tf and a polynomial approximation of this over an interval
of time. The higher order derivatives of these functions are very different, and so,
consequently, are the preceding corresponding series. In fact, we can easily verify
the convergence of the series for exponential or sinusoidal functions whose time or
frequency constants are relatively small, but the preceding representation is of
limited use for these particular cases.
For the example considered, we can show that we have convergence of the series
if the series of the general term
nn
tf 4
~
converges. Recall, however, that, from
a mathematical point of view, the solutions established for the partial differential
equation does not require the existence of derivatives for the given function
tf .
The preceding results can equally be obtained by means of a Laplace transform
(Appendix 1) in the asymptotic approximation for large periods of time.
The regular perturbation of the solution to a non-linear partial differential
equation is more difficult (section 6.4.2.3), and in general we can only obtain the
first terms of the development. Examples of this kind of development (Blasius
series, Görtler series, etc.) are found for boundary layer equations ([SCH 99], [YIH
77]).
The method of regular perturbations can also be applied in acoustics and
energetics. Consider the geometry of Figure 6.13 in which the cylinder of base C is a

General Properties of Flows 305
solid, with constant physical properties, subjected to a heat release of volume power
P(t) and whose external wall is maintained at constant temperature T = 0.
The thermal conduction equation for this solid and the associated boundary
conditions:
;)( '
w
w
TtP
t
T
C OU
with: (,) : (,,) 0yz C T yzt
can be immediately reduced to equation and boundary conditions given in [6.69].
6.4.3. Singular perturbations
6.4.3.1. Introduction
In section 6.4.2 we assumed that the differential equation could be solved with
respect to the first derivative such that the unperturbed equation (
H
=0) possesses a
differentiable solution. This is not the case if the coefficient of the derivative tends
to zero with
H
faster than the other coefficients. Let us examine the elementary
example of the following differential equation in which the parameter
H
is now the
coefficient of the derivative )(tx
:
001)(' H xtxtx [6.72]
The solution is:
H ttx exp1.
For
H
to tend to zero, it is easy to follow the evolution of the solution towards its
discontinuous limit (Figure 6.12b) made up of the half-line (x = 1, t > 0) and the
origin O. Letting
H equal to zero in equation [6.72], we obtain the solution 1 x
which is valid nearly everywhere, and we can no longer satisfy the initial condition
posed at the origin for this part of the solution (called the external solution). We note
that the family of functions
H
,tx does not converge uniformly towards its limit for
H
= 0.
It is therefore necessary to perform a particular study over a small interval in the
neighborhood of the origin where the solution undergoes significant variations over
a small distance (internal solution) in order to recover the boundary condition which
is not satisfied.
The external solution can also undergo a regular perturbation due to the small
parameter
H
. For example, the solution of the following differential equation:
001 H xxx
306 Fundamentals of Fluid Mechanics and Transport Phenomena
does only differs from the preceding equation by the coordinate 1 +
H of the
horizontal asymptote.
6.4.3.2.
Methods for studying singular perturbations
The existence of a singular perturbation is related to the presence of a singularity
for the limit solution of a system of differential equations. This phenomenon is
encountered in diverse circumstances and notably in the case of the lowering of the
order of a differential system in which we impose
H
as zero, or when the limit
solution or one of the derivatives involves a discontinuity on the interval of the
study. We will limit ourselves here to the study of a very simple case in order to
illustrate the general method by which we discuss such problems.
The direct numerical study of a problem involving singular perturbations often
presents difficulties on account of the very large disparity in the characteristic scales
found in different regions of the study. This point can obviously involve difficulties
for numerical methods in fluid mechanics. It is therefore particularly interesting to
directly obtain information independent of the exact solution (often very difficult) of
the differential problem which is posed. We will illustrate this using a very simple
case; the general analysis method involves a number of stages:
1) searching for the external solution: a study of the order of magnitude of the
solution which is assumed to vary regularly over the interval under study allows us
to obtain equations which are satisfied by the external solution;
2) we then try to identify a contradiction with respect to the data of the problem
in order to identify the singularity to study;
3) a new examination of the order of magnitudes of the terms of the equation
provides information pertaining to the scales of the singularity to be studied;
4) it is then possible to identify the equations of the differential problem in the
singular zone (internal solution), these resulting from simplifications of the
complete problem;
5) we then discuss the boundary conditions to be associated with the two
preceding problems for matching their solutions.
6.4.3.3.
An elementary example
The example of section 6.4.3.1 is too simple because the internal solution and the
exact solution are identical. Consider the following differential problem:
001)( xttxtx
D
H
[6.73]

General Properties of Flows 307
Ignoring the results of the last example, let us apply the methodology described
above:
1) We first look for the external solution by supposing that the unknown function
has variations of the order of one on the intervals of the same order of magnitude.
To
O(
H
), differential equation [6.73] reduces to:
ttx
D
1)(
The equation obtained is here an algebraic relation (a zero order differential
equation) which explicitly gives the external solution which is valid nearly
everywhere.
2) The condition that x(t) be zero at the origin is not fulfilled. We must therefore
complete the preceding solution by an internal solution on an interval with a
different scale to the interval where the external solution is valid, otherwise we will
only recover the latter. Let
G
be the order of magnitude of the length scale of the
interval over which the neglected term
x
H
must be taken into account.
The interval sought of scale
G
must be situated at the origin. In effect, if this was
not the case, we would have
between this interval
o(1)
and the origin a finite interval
on which the results of the external zone would be applicable; the function x would
be equal to 1+
D
t and would not therefore be zero at the origin, which would imply
that nothing had been solved. The only reasonable possibility is therefore to place
our small interval
G
in the neighborhood of the origin.
3) The order of magnitude of
G
can be obtained by supposing that the term
H
x' is
of the same order as that of the variations of x, i.e. of the order of 1:
DG
G
H
D
H
|||
11
1)(
ttxtx
We can deduce from this that
H G
, and we need to study the behavior of the
solution in an interval of amplitude
H
close to the origin.
4) We perform the change of variable:
K
H
K
Xtx
t
Neglecting the terms of order
H
, equation [6.73] can be written:
001)(
XXX
KK

308 Fundamentals of Fluid Mechanics and Transport Phenomena
Its solution satisfying the condition at the origin can be written:
K
K
eAX
1
It tends to A when
K
tends to infinity.
5) We now have two pieces of the solution (Figure 6.14b) which we need to
match. This procedure appears relatively empirical and we will consider only small
values of
H
. We see that as
H
tends to zero, the value
DH
1 of the external solution
for
x
=
H
tends to 1. We therefore adopt the following simple matching rule.
The limit of the internal solution
F
(
K
) for
K
becoming infinite is equal to the
limit of the external solution
x
(
t) when t tends to 0
:
t
x
X
t 0
limlim
ofo
K
K
y
(b)
1
O
x
internal solution:
1-exp(-t/
H
)
exact solution
external solution:
x = 1+
D
t
1
O
y
x
exact solution
H
(a)
H
asymptote: x = 1+
D
t
Figure 6.14.
(a) Exact solution of differential problem [6.73];
(b) matching of external and internal solutions
This rule provides the boundary conditions which were missing for the internal
solution and leads to a value of 1 being assigned to the constant
A
. We thus obtain
the internal solution:
( ) 1 with: /
X e t %
In fluid mechanics, the internal solution is called a
boundary layer
. Such
singularities are encountered in all domains of physics (skin effect in
electromagnetism, penetration depth of an evanescent electromagnetic or acoustic
wave, etc.). We will see other examples in problems of heat transfer or chemical
reactions with or without flow.
General Properties of Flows 309
The singularity can also consist of a discontinuity of the first or second
derivatives.
Perturbation problems can also present other characteristics. Consider for
example, the following lightly damped oscillator (section 6.3.1.1):
0
xxx
H
The friction term
x
H
is a perturbation of the undamped equation. The
modification of the oscillatory solution due to a damping term
2t
e
H
has an effect
of order
H
over a duration
O(1), but the final result is the suppression of the
movement. The perturbation effects due to friction are cumulative.
More complete developments on singular perturbations can be found in
specialized textbooks ([COL 68], [HIN 91], [NAY 81], [VAN 75]).
6.5. Quasi-1D flows
6.5.1. General properties
6.5.1.1.
Assumptions
Many flows can present a quasi-1D character, in other words the evolution scales
of phenomena differ depending on whether we follow the principal direction of the
flow or the transverse directions.
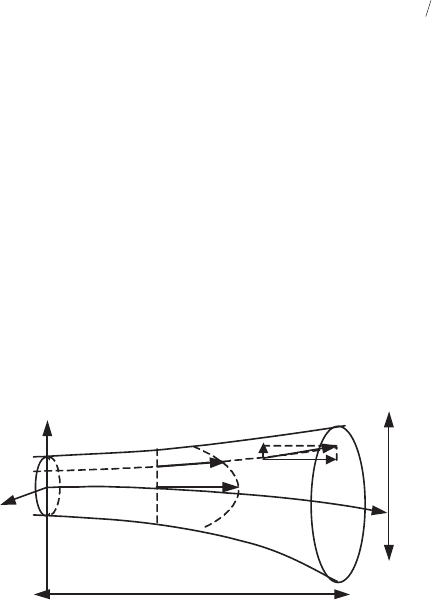
M
x
O
y
d
L
u
v
V
G
z
Figure 6.15.
Quasi-1D flows
The basic assumption of a viscous quasi-1D flow is that the cross-section and
direction of a stream tube vary quite slowly (Figure 6.15). The thickness
d
of the
domain of study is small compared to its length
L
(
d
<<
L
). We consider the
coordinate on a curve oriented along O
x
, more or less parallel to the stream tubes
(the axis of a pipe, jet or wall, etc.) and the orthogonal coordinates in cross-sections

310 Fundamentals of Fluid Mechanics and Transport Phenomena
orthogonal to O
x
. The local coordinates defined by the curvilinear abscissa
x
and the
orthogonal coordinates
zy
, in cross-sections constitute a
coordinate system which
is locally Cartesian
. These assumptions allow us to write the
balance equations in
Cartesian form
in this zone.
We furthermore assume that the variations
G
f
of the quantities
f
studied are more
or less of the same order of magnitude over the distances
d
and
L
.
6.5.1.2.
Approximations
The following properties result from the preceding assumptions:
1) Partial derivatives of a quantity in the directions y or z are an order of
magnitude greater than the corresponding axial derivative in the direction Ox. In
effect
Lfxf
G
|ww
and
dfyf
G
|ww
lead to:
2
2
2
2
2
2
y
f
L
d
x
f
and
y
f
L
d
x
f
w
w
|
w
w
w
w
|
w
w
This results in vectors of the form k
fgrad (for example, the thermal or mass
flux densities
G
q
G
, etc.) are perpendicular to the axis Ox and that we only take into
account the two components k
yf ww and k zf ww of the flux density
G
q
G
.
2) The diffusion term
G
qdiv
G
of the balance equation of a scalar quantity G is
therefore reduced to the sum of the transverse derivatives
yq
Gy
ww
and
zq
Gz
ww .
3) The transverse components v and w of the velocity are small compared with
the axial component u ( uv and uw ). In effect, assuming the flow to be
incompressible, the volume balance can be written:
0
w
w
w
w
w
w
z
w
y
v
x
u
If variations of the cross-section exist, the transverse velocity is not zero, but it is
very small, in order to ensure the inclination of the velocity with respect to the axis
Ox, of order d/L. Assuming the 2D problem (w = 0) in order to simplify matters, the
two derivatives
xu ww and yv ww have the same value (sign excepted). An order of
magnitude analysis shows that:

General Properties of Flows 311
d
v
y
v
L
U
x
u
|
w
w
||
w
w
i.e., sign excepted,
LUdv | .
No simplification is possible in the mass conservation equation.
The result of this evaluation of the velocity components is that the dominant
terms of the viscous stress tensor are the tangential components
yu ww
P
and
zu ww
P
(friction forces in the Ox direction).
4) The material derivative of a scalar quantity conserves its general expression
in the quasi-1D approximation.
Consider the material derivative
y
g
v
x
g
u
t
g
dt
dg
w
w
w
w
w
w
of the quantity g. The
two convection terms are of the same order:
L
g
U
d
g
L
d
U
y
g
v
L
g
U
x
g
u
GGG
|
w
w
|
w
w
5) On the other hand, an analogous order of magnitude calculation shows that the
small value of the transverse components of the velocity leads to the transverse
accelerations dv/dt and dw/dt
being negligible with respect to the axial acceleration
du/dt.
6.5.1.3.
Local balance equations
Taking account of the preceding approximations, balance equation [4.3] for the
volume quantity
g can be written:
z
q
y
q
dt
dg
gVdiv
t
g
Gz
Gy
G
w
w
w
w
w
w
VU
G
[6.74]
By way of example, the dynamic equation following Ox [4.21], for a Newtonian
fluid, can be written:
¸
¸
¹
·
¨
¨
©
§
w
w
w
w
¸
¸
¹
·
¨
¨
©
§
w
w
w
w
w
w
»
»
¼
º
«
«
¬
ª
w
w
w
w
w
w
w
w
z
u
zy
u
y
f
x
p
z
u
w
y
u
v
x
u
u
t
u
x
PPUU
[6.75]

312 Fundamentals of Fluid Mechanics and Transport Phenomena
In a plane 2D flow, we obtain for a fluid with constant physical properties
(where p
g
is the driving pressure):
2
2
y
u
x
p
y
u
v
x
u
u
t
u
dt
du
g
w
w
w
w
»
»
¼
º
«
«
¬
ª
w
w
w
w
w
w
PUU
[6.76]
Finally, as the transverse accelerations dv/dt and dw/dt are negligible with
respect to the axial acceleration du/dt, the viscous stress terms of the transverse
equations are equally negligible with respect to the corresponding term in the axial
dynamic equation. The transverse equations reduce to:
0
w
w
w
w
z
p
y
p
gg
The pressure (or driving pressure) distribution in a cross-section is hydrostatic,
but it depends on x and t.
Energy equation [4.51] can thus be written in the quasi-1D approximation:
¸
¸
¹
·
¨
¨
©
§
w
w
w
w
¸
¸
¹
·
¨
¨
©
§
w
w
w
w
¸
¸
¹
·
¨
¨
©
§
w
w
¸
¸
¹
·
¨
¨
©
§
w
w
°
°
°
¿
°
°
°
¾
½
w
w
z
T
zy
T
yz
u
y
u
dt
ds
T
dt
dp
dt
dh
x
u
p
dt
de
T
i
i
OOVPP
U
U
U
2
2
[6.77]
Dissipation function [4.56] can be simplified by only considering the dominant
strain rates
yu ww and zu ww . We find immediately:
2
2
¸
¸
¹
·
¨
¨
©
§
w
w
¸
¸
¹
·
¨
¨
©
§
w
w
)
z
u
y
u
PP
[6.78]
6.5.1.4.
Parabolic character of the quasi-1D equations
Consider first convection equation [6.74] in which the velocity field is assumed
to be given. This presents a structure analogous to the heat equation, i.e. it has a
dissymmetry in the order of the derivations with respect to the variables: second
derivatives with respect to y and z are encountered, the derivatives with respect to x
and t being only first order. This results in a parabolic behavior with respect to the
variables x and t: the temperature distribution in a cross-section of coordinate x at
