Peube J-L. Fundamentals of fluid mechanics and transport phenomena

Подождите немного. Документ загружается.

Measurement, Representation and Analysis of Temporal Signals 403

about 100 m/s

-1

), whereas the smallest problem of heat transfer generally involves

fluctuations of some about 10°C. For example, a local, instantaneous measurement

sensor of velocity or of temperature characterizes phenomena associated with the

flow and the heat transfer depending on the circumstances (section 7.2.4).

On the other hand, the

respective contributions

of the acoustic modes and

of the convective modes to pressure variations may be of the same order. In

effect, we have seen (section 5.3.2) that we have:

– on the acoustic characteristic curve:

ucp

– on the convective characteristic curve:

 VVp

The ratio of these pressure fluctuations is thus:

As the Mach number is small at low velocity (M ~ 0.05 to 0.15 in ventilation

problems for example), the factor

M1 is quite large and it compensates the small

acoustic velocity fluctuations compared to the turbulent velocity fluctuations. This

results in

pressure fluctuations due to local turbulence effects, which are of the same

order of magnitude as acoustic pressure fluctuations.

A pressure probe (microphone) measures the local pressure independently of its

origin

and without knowing on which characteristic curve it is transmitted: it is no

longer possible to distinguish acoustic fluctuations from those due to local velocity

fluctuations. This problem is well known to those who measure sound: a

microphone placed in a flow does not only measure noise. Listening to the pressure

signal acquired by a microphone placed in the wind we are immediately aware of a

parasite “sound” due to the wind. This “sound” is not of an acoustic nature, but

rather a signal that corresponds to local pressure fluctuations associated with the

flow created around the microphone. Measurement of sound in the presence of wind

requires suitable precautions in order to reduce the impact of parasitic phenomena

(for example, “anti-wind” foam covers on microphones).

The separation of turbulence and acoustic pressure components is an important

and extremely difficult problem, since it corresponds to Navier-Stokes solutions for

which the theory of characteristics curves is in practice not applicable. This

404 Fundamentals of Fluid Mechanics and Transport Phenomena

separation between acoustic and turbulence signatures can only be made possible if

additional information is available: for example the periodic sound due to a

propeller can be extracted from a signal containing random turbulence fluctuations.

7.4.4.4.

The study of unsteady flows

The velocity, pressure or temperature fields associated with unsteady flows are

now accessible by means of experimental methods described in section 7.2.6.3; on

the other hand, the different methods of time-frequency analysis allows the temporal

and spectral characteristics of flows to be identified. These modern methods allow

us to consider the vast domain of experimental unsteady fluid mechanics, provided

that experiments can be performed in a reproducible manner (which means that

different realizations obtained are identical (section 7.2.6.3)). The identification of

unsteady flow structures and, in particular, the dynamics of vortex interactions

constitutes a domain of study which is relatively unexplored.

We will see that turbulence, being by its nature unsteady and broadly 3D, is

largely the result of interactions between inviscid fluid structures (turbulent energy

cascade [MAT 00]). The origin of turbulence is furthermore associated with the

development of flow instabilities issued from pre-existing perturbations. The

elementary mechanisms of these highly unsteady interactions are poorly understood.

For these reasons, we have focused on signal-processing and experimental methods

that can be used in a broad range of applications where unsteady phenomena are

encountered in possibly rotational flows These methods allowed for example the

acquisition of experimental data for the problem discussed in section 5.6.2.

Chapter 8

Thermal Systems and Models

This chapter is dedicated to the modeling of systems. The perspective developed

in automatic control and the corresponding methods are outlined. In addition to the

mathematical properties of thermodynamic balance equations and the measurement

and signal processing problems, these provide a general framework for the study of

the representation and evolution of physical systems. Using some basic heat

conduction problems in media at rest, the methods can be easily proved on account

of the linear properties that these present.

8.1. Overview of models

8.1.1. Introduction and definitions

In Chapters 1 to 4 we studied how to describe a physical system in the context of

thermodynamics. The equations for continuous media are hardly useable except for

very simple problems and any more complex system can only be represented by

making approximations, which it must be possible to evaluate. We will limit

ourselves in this chapter to state representation in which a given thermodynamic

system is represented as a group of sub-systems in instantaneous equilibrium. This

makes it possible to define the state variables of each sub-system. The partial

differential equations which represent the continuous medium are thus replaced by

partial differential equations describing the evolution of a restricted number of

variables. The general study of systems is derived from automatic control and signal

processing which provide, as in thermodynamics, general principles which cannot be

ignored. We will recall here the ideas that are necessary for the establishment of

406 Fundamentals of Fluid Mechanics and Transport Phenomena

models in fluid dynamics and heat and mass transfer, by limiting ourselves to the

study of thermal systems, whose damped character simplifies the discussion.

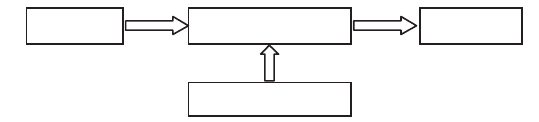
A system is a material ensemble that exchanges quantities with the exterior. We

act on the system(s) by means of inputs, which are imposed variables (a

temperature, a mass flow, pressures, etc.); these inputs lead to modifications of the

system which are manifest in observed and measured effects, which constitute the

outputs of the system. The inputs are therefore causes and the outputs are

consequences.

Syste

OutputsInputs

Initial conditions

Figure 8.1. Scheme of a system

A system is said to be causal (with respect to a variable) if the conditions which

determine its state and its outputs for a value of the variables x

result from data for

values of the variable x which are less than or equal to x

. This idea of causality

simply translates the mathematical properties associated with the parabolic or

hyperbolic character of the system towards certain variables or groups of variables

of the model that is used. While it is obvious for the time dimension (section

1.1.1.3), this idea, which is used in automatic control and signal processing, can also

be applied to transport and propagation phenomena (sections 5.3.2 and 5.4.5.4).

The description and knowledge of a system can be achieved by means of a

model, which can only be established if the system is observable, in other words if

we can measure the data necessary for its establishment. This condition obviously

depends on the nature of the system and the objective of the modeling.

The control of a system is an action that is often necessary for diverse reasons:

control of temperature in a zone, of a flow structure, a sound level, etc. A system is

said to be controllable if, from any initial state of the system, it is possible to act on

certain inputs in order to bring the system to a desired state.

A system is said to be instantaneous if its state and its outputs at a given instant

depend only on the inputs at that instant. This definition can be applied to any

system whose sub-systems are in mutual thermodynamic equilibrium. A system is

said to be dynamic if it is not instantaneous.

Thermal Systems and Models 407

Systems exhibiting hysteresis present the particularity that the stationary solution

corresponding to fixed inputs depends on their history (state variables at the initial

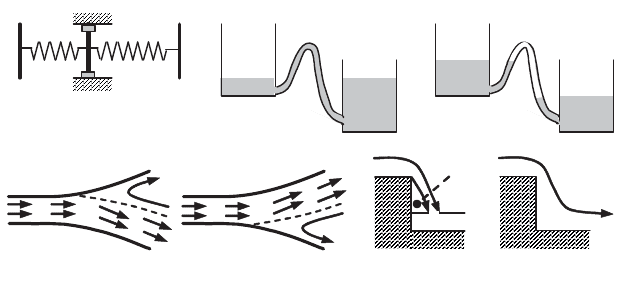
state and the past evolution of the inputs). Let us take the example of an oscillator

comprising a mass P placed between two springs and subjected to a friction force on

a fixed wall. If the friction is caused by a fluid, the equilibrium position of the point

P is unique, the tension in the springs being therefore equal. In return the existence

of a solid source of friction in P means that the final position of the point P also

depends on the movement history (Figure 8.2a).

Flow systems with hysteresis are encountered not only with fluids whose

behavior laws involve a solid friction (Bingham fluid), but also for Newtonian

fluids. This phenomenon is thus associated with the existence of two possible steady

solutions for a flow with fixed conditions. This circumstance may be due to diverse

phenomena such as the feeding of a siphon (Figures 8.2b and 8.2c), reattachment of

a flow on a curved surface (Figure 8.2d and Figure 8.2e), the flow of water over a

weir depending on whether the sheet of water is aerated (or ventilated) or not

(Figure 8.2f and Figure 8.2g), etc. The observed solution can vary depending on the

manner we seek to achieve it by.

(a) (b) (c)

(d)

air

water

(g)

water

(e) (f)

Figure 8.2.

Systems with hysteresis – (a) springs with dry friction; set of 2 tanks with feuded

(b) or not (c) siphon; flows in a divergent pipe (d) and (e); weir with aerated water sheet (f)

or non-aerated water sheet (g)

In addition, unknown perturbations (noise) are always present to varying degrees

in these inputs and can have diverse effects (“instabilities”). The idea of a stable

system is difficult to define, because it depends on the nature of the applied

perturbations and the properties of the response of the system. Stability is a complex

problem and of extreme importance in fluid mechanics ([SCH 99], [YIH 77]).

408 Fundamentals of Fluid Mechanics and Transport Phenomena

A system is said to be stationary or time-invariant if the outputs corresponding to

a given set of inputs do not depend on the instant at which the inputs are applied.

The equations of a time-invariant system are not influenced by a change of the time

origin. Systems whose structure and physical properties only depend on the state

variables are time-invariant. The same is not true of systems whose parameters

depend on external conditions which vary with time (for example, the flow of a

liquid in the process of polymerization, the action of an obstacle with an incidence

angle D(t) which is imposed in accordance with some external law, etc.).

A linear time-invariant system (LTIS), which is also known as a linear

stationary system (LSS), presents in addition the property of linearity: effects

proportional to the causes which produce them. These systems are described by

constant-coefficient linear models. Apart from some very specific cases, a system

with a non-uniform flow is not linear. The heat transfer of mass by diffusion is often

linear, even in flows, provided the temperature or concentration does not cause the

physical properties of the fluid to change. Coupling between different phenomena

and in particular chemical reactions in flows suppresses this linearity property. The

reader can verify these properties for the general equations in Chapters 1 to 4.

8.1.2. Modeling by state representation and choice of variables

In automatic control, state representation of a discrete system is a model of the

form [8.1] which represents its evolution:

UEXDYUBXA

....   [8.1]

The state vector X is a set of n variables which characterize the state of the

system. The state representation is also called the internal representation. This

definition is no different in principle to the definition which was given in Chapter 1

where extensive and intensive variables were used as state variables. However, in

automatic control the components of the vector X can be any variables which

characterize the state of the system. The matrix A is a square matrix of rank n. It

characterizes the make-up of the system and of the sub-systems which correspond to

the choice of the state vector X.

The vector U is the input vector; it is of dimension p and corresponds to different

actions on the system. It does not in general have the same dimension as the vector

X, and the matrix B is a rectangular matrix of dimension n

I.e. the coefficients of operators in the equation; the inputs are not parameters of the system

here.

Thermal Systems and Models 409

The vector Y is the output vector; it is of dimension q and it comprises the

different results desired for the problem posed. It does not in general have the same

dimension as the vectors X and U. In what follows, we will take E = 0 (the system is

thus called proper).

The representation of the state of a system is not unique as the variables can be

chosen in different ways or can be modified by changes of variable. Furthermore,

the components of the state vector can be related when we are limited to particular

operation regimes as we will see on numerous occasions in the remainder of this

chapter (section 8.3, section 8.5 and section 8.6). However, the systems studied in

this work are constituted of a matter, which obeys the laws of thermodynamics. The

form of differential system [8.1] is analogous to that of the balance equations, but

the coherence with the laws of thermodynamics is only effective because of a

suitable choice of state vector components (section 1.2.1).

We also saw in section 5.1.1 that a system of first order differential equations

can be written in the form of a scalar differential equation of order n for one scalar

variable. This equation can also be written in the form of differential system [8.1],

the state vector X (t) being replaced by a state vector having the same number of

components, but constituted of a variable x

( t) and of its n – 1 first derivatives. By

reconsidering the calculation of section 5.1.1 the reader will see that the inputs

obtained for this differential system imply the initial inputs and their n – 1 first

derivatives. This form of state-representation is known as the form of observability

([DOU 95], [GUP 83], [KUO 02]). We will use this for a particular case in section

8.4.2.2.

For a non-linear system the matrices A, B and D can be functions of the state

vector X of the system.

For a system involving an instantaneous response, the derivative

dtd

takes on

small values compared with second order terms; the inertia of this system is weak

and the extensive quantities which result from the inputs are instantaneously

transferred to the sub-systems. The differential character and the idea of the initial

state of system [8.1] have disappeared and the representation is reduced to an

algebraic system:

XDYUBXA .,0.. 

We note that in the case of an impulse input, the response and the outputs of an

instantaneous-response system involve a discontinuity. As nature does not contain

discontinuities in such situations, we have in reality a continuous transitional regime

involving a singular perturbation (section 6.4.3).

410 Fundamentals of Fluid Mechanics and Transport Phenomena

In the case of a time-invariant system, the coefficients matrices A, B and D are

independent of time, but they may be functions of the state variables: the structure of

the system remains unchanged over the course of time. If the system is furthermore

linear, they are constant and we have a time-invariant linear system.

For a system made up of continuous media, the system of differential equations

[8.1] is replaced by partial differential equations. The inputs are either boundary

conditions or volume heat source terms. When the physical properties depend on the

temperature, these equations are non-linear. On the other hand, if the properties are

only a function of the coordinates, we have a time-invariant linear system. In the

presence of a flow, the temporal derivative

becomes a material derivative

dtd in the case of a Eulerian representation.

8.1.3. External representation

The external representation of a system consists of considering it as a black box

that links inputs and outputs. However, the conservation laws of extensive quantities

must be considered between the inputs and outputs of a system. The permanent

production of mechanical or thermal energy is only possible if energy is provided to

the system; the same goes for mass, chemical species in the absence of chemical

reactions, etc. The consequences of the second principle of thermodynamics are

directly manifest in the constraints upon the entropy of the system studied. In other

words, the system can only evolve within the bounds of possible processes. In fact,

the coherence between automatic control and thermodynamics is only ensured if the

global thermodynamic balances are satisfied for state representation [8.1] of the

system.

In practice, a system is often characterized using incomplete data which are

obtained by means of indicial experiments: we modify one variable by quickly

increasing it by a small amount (Heaviside unit step) and we record the evolution of

the outputs. If the response of these is not instantaneous, the system undergoes an

internal evolution which must be characterized. For example, the progressive

response of a system to an instantaneous increase of the mass flow rate or of the

input temperature indicates the capacity of the system to accumulate matter or mass

in its interior. We must therefore introduce an internal state variable to the system

(volume or pressure for a compressible fluid, calorific capacity, etc.) or,

equivalently, we must introduce terms involving temporal derivatives in the external

representation (section 8.4.2.2).

The formulae used by engineers for over two centuries are external

representations which correspond to operating conditions of the system, which are

more or less well (or badly) defined. Models which use continuous-medium

Thermal Systems and Models 411

equations are state representations in which the inputs and outputs take the form of

simple formulae corresponding to the system studied under particular conditions.

These simplified external representations are then often used in more general

conditions in which their degree of approximation is difficult to evaluate. For

example, in a flow system comprising a pipe of length L and of diameter D, in which

the mass flow

q is given (as an input), an interesting output is the pressure

difference p

in the flow between the input and output sections. This will depend,

for example, on the mass flux, on the viscosity, on the density of the fluid and on the

dimension k of the roughness of the pipe. We will therefore have, in non-

dimensional form for the pressure

/ '

Re,

[8.2]

where S is the area of a reference cross-section. The non-dimensional coefficient /

of the driving pressure loss is a function of the dimensionless data (Reynolds

number Re and roughness parameter

k/D

) (section 4.6.1.3.4), this function having

been determined by semi-empirical considerations and experiments.

Approximate external representations can be used in the study of more complex

systems modeled by means of state representations. For example, in models of large

dimension in continuous media studied by means of numerical solution of the

Navier-Stokes equations by finite difference or finite volume methods, boundary

layers in the vicinity of walls are too thin to be discretized (section 6.5.3.3). The

friction on the walls is therefore taken as a boundary condition of certain elements

and it is expressed by a global relation analogous to [8.2] as a function of the

characteristics of the velocity field next to these elements.

8.1.4. Command models

The objective of a

knowledge model

is to describe quantitatively an evolving

system and its internal and external transfers, with a precise enough description of

the physics of processes both sufficient and pertinent.

command

model

defines actions whose objective is to cause the system to

evolve towards a given state. We seek only to represent the evolution of the system

in the vicinity of a given state of operation; a linear relation between input and

output variations is often sufficient. We must however note that this rather blind

manner of proceeding assumes that the

internal structure of the system remains

unchanged

412 Fundamentals of Fluid Mechanics and Transport Phenomena

The pragmatic approach, from the point of view of control and command of a

system, often consists of considering only the observable outputs such as the

temperature, the pressure, certain concentrations of chemical species, fluxes, etc., at

points in an industrial system where measurement is possible. The objective of

control is to fix the values of certain output variables (temperature, pressure, etc.) or

certain state variables. The commands act on the input variables which may be of

the same nature as the output variables. In practice, we content ourselves with the

examination of the response of the system to perturbations such that we can estimate

the corrections which need to be made. The study of a response curve allows us to

define the global order of a system.

8.2. Thermodynamics and state representation

8.2.1. General principles of modeling

8.2.1.1.

Introduction

System [8.1] is of a differential nature with respect to time. We must add an

initial condition for the state variable )0(

. The procedure in automatic control

consists of only considering the state-representation form and “forgetting” the origin

or the physical interpretation of this. In practice, the real problem of establishing a

model lies in the choice of variables for the state vector

, which must be performed

in a manner which conforms to the laws of thermodynamics.

Our study of thermodynamics in Chapters 1 to 4 showed the following general

mathematical structure:

–

extensive quantities

satisfying the conservation laws (balance equations)

defined for each sub-system regardless of its state of imbalance;

–

intensive quantities

which are only defined for discrete systems in equilibrium,

or for continuous media with an assumption of local equilibrium;

–

fluxes of extensive quantities

associated with thermodynamic imbalance

characterized by differences or gradients of the intensive quantities;

–

relations between intensive and extensive variables

(equations of state) and

phenomenological laws for the thermodynamic fluxes of the extensive quantities.

Modeling a sub-system leads us to define and choose the variables necessary for

its dynamic description, and in particular

stocks and fluxes of extensive quantities

each instant. The discrete equations result from the application of the balance

equations to each of the sub-systems. The extensive quantities are additive and they

are always defined for any given sub-system.