Peube J-L. Fundamentals of fluid mechanics and transport phenomena
Подождите немного. Документ загружается.

Thermal Systems and Models 423
being greater as the thermodynamic imbalance is more pronounced. We will limit
our discussion here to linear systems which only possess modal solutions allowing
an analytical treatment. The methodologies for writing balance equations are
independent of linearity properties. The variation of physical properties as a function
of the state variables often leads to weak non-linearities, which do not change the
general properties and the orders of magnitude obtained. We will first study three
examples of simple discrete thermal systems, then two problems of continuous
media (thermal walls).
8.3.1.2.
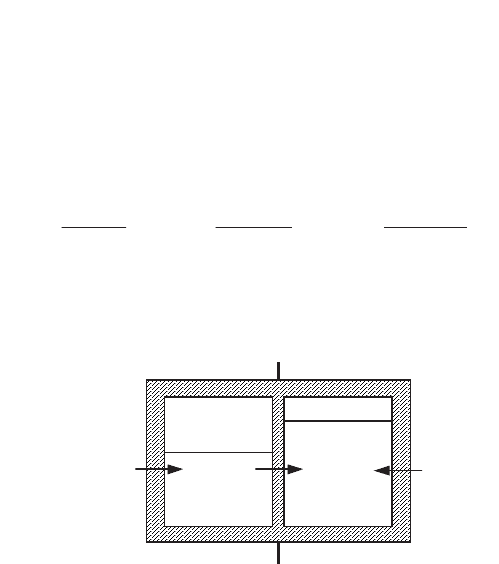
Models with two sub-systems at constant temperature
Consider a time-invariant linear system which is composed of two blocks E
1
and
E
2
of width
A
, of specific heat C and separated by a thermal resistance R. Let us then
consider a representation of this system by means of
two sub-systems of uniform
temperatures
tT
1
and
tT
2
(Figure 8.7). Each of these two sub-systems is
separated from the exterior by another thermal resistance R’.
A thermal resistance is an element of small thickness which transmits heat in a
quasi-instantaneous manner; the thermal flux
M
which crosses this element is
proportional to the temperature difference between its external faces. The fluxes
M
1,2
,
M
1
w
and
M
2
w
received by each sub-system (Figure 8.7) are:
.
'
;
'
;
22
2
11
1
21
2,1
R
TT
R
TT
R
TT
ex
w
ex
w
MMM
[8.20]
The initial temperatures
)0(
1
T and )0(
2
T and the external temperatures T
1ex
(t)
and
T
2ex
(t) are given.
T
1ex
T
1
T
2
T
2
ex
M
2w
M
1
w
M
1,2
E
1
E
2
RR' R'
m
m
Figure 8.7.
Thermal conducting system with two equilibrium sub-systems
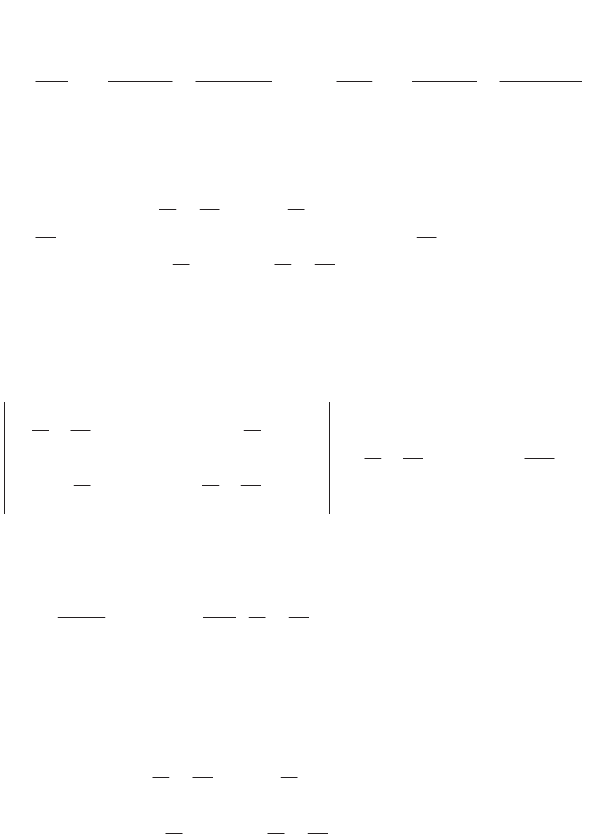
424 Fundamentals of Fluid Mechanics and Transport Phenomena
Taking account of [8.20], the energy balance of each sub-system allows the
obtaining of a differential system for the temperatures
tT
1
and
tT
2
:
.
'
;
'
2212211211
R
TT
R
TT
d
t
dT
mC
R
TT
R
TT
d
t
dT
mC
exex
or in matrix form:
¸
¸
¹
·
¨
¨
©
§
¸
¸
¹
·
¨
¨
©
§
¸
¸
¸
¸
¸
¹
·
¨
¨
¨
¨
¨
©
§
¸
¸
¹
·
¨
¨
©
§
¸
¸
¹
·
¨
¨
©
§
¸
¸
¹
·
¨
¨
©
§
ex
ex
T
T
R
T
T
RRR
RRR
T
T
dt
d
mC
2
1
2
1
2
1
'
1
'
111
1
'
11
[8.21]
Searching for solutions of the form 4
rt
e for the homogenous system associated
with [8.21] gives the eigenvalue equation (characteristic equation):
0
1
'
11
'
111
1
'
11
2
2
¸
¸
¹
·
¨
¨
©
§
¸
¸
¹
·
¨
¨
©
§
¸
¸
¹
·
¨
¨
©
§
R
mCr
RR
mCr
RRR
R
mCr
RR
This has two roots (eigenvalues):
¸
¸
¹
·
¨
¨
©
§
'
121
;
'
1
21
RRmC
r
mCR
r [8.22]
From these we can find the components (4
i
1
, 4
i
2
) of the eigenvectors 4
i
(i = 1,
2), which are solutions to the system of equations:
¸
¸
¹
·
¨
¨
©
§
4
4
¸
¸
¸
¸
¸
¹
·
¨
¨
¨
¨
¨
©
§
¸
¸
¹
·
¨
¨
©
§
¸
¸
¹
·
¨
¨
©
§
¸
¸
¹
·
¨
¨
©
§
4
4
2
1
2
1
'
111
1
'
11
i
i
i
i
RRR
RRR
mCr
We obtain:
– mode 1 (symmetric, i = 1, with 4
11
= 4
12
= 1):

Thermal Systems and Models 425
'/exp;
'
1
12111
mCRtTT
mCR
r
– mode 2 (antisymmetric, i = 2, with 4
21
= 4
22
= 1):
¸
¸
¹
·
¨
¨
©
§
¸
¸
¹
·
¨
¨
©
§
¸
¸
¹
·
¨
¨
©
§
'
12
exp;
'
121
22212
RRmC
t
TT
RRmC
r
The general solution of the homogenous system can be written:
.expexp,expexp
2211222111
trctrcTtrctrcT
Let T
1e
(t) and T
2e
(t) be a particular solution of [8.21] (“established” solution);
we obtain as a general solution to [8.21]:
tTtrctrctT
tTtrctrctT
e
e
222112
122111
expexp)(
expexp)(
The integration constants c
1
and c
2
can be calculated with initial conditions;
>@
>@
20000
20000
21212
21211
ee
ee
TTTTc
TTTTc
The decomposition of the solution into two modes can be written:
>@
>@
>@
>@
2exp2/
2exp2
2122212
2111211
tTtTtrctTtTt
tTtTtrctTtTt
ee
ee
T
T
The fast mode
T
2
(t) corresponds here to the establishment of internal equilibrium
of the system, while the slow mode
T
1
(t) represents the establishment of equilibrium
between the system and the exterior. For a system isolated from the exterior (infinite
R’), we obtain:
¸
¸
¹
·
¨
¨
©
§
mCR
t
TTtTtTTTtTtT
2
exp00)()(,00)()(
21212121
8.3.1.3.
System with three components in series
Consider now the system shown in Figure 8.8 consisting of three sub-systems
E
1
, E
2
and E
3
. The component E
3
, isolated from the exterior, is in contact with

426 Fundamentals of Fluid Mechanics and Transport Phenomena
E
1
and E
2
via the thermal resistances of the same value R/2. As before, the sub-
systems E
1
and E
2
are each in contact via a thermal resistance of the same value R’,
with the external medium at temperature T
i
ex
(t) (i = 1,2). Sub-system E
3
is isolated
from the exterior.
The energy balance equations can be written:
R
T
R
T
R
T
d
t
dT
Cm
R
T
R
T
RR
T
dt
dT
mC
R
T
R
T
RR
T
dt
dT
mC
ex
ex
3213
23
2
2
13
1
1
4
.
22
'
;
'
2
'
12
;
'
2
'
12
¸
¸
¹
·
¨
¨
©
§
¸
¸
¹
·
¨
¨
©
§
[8.23]
T
1ex
T
1
T
2
ex
M
2p
M
1p
M
1,3
E
1
T
3
E
3
T
2
E
2
M
3,2
R/2 R/2 R' R'
m
m'
=
H
m
m
Figure 8.8.
System with three sub-systems (first example)
The system of equations can be written in matrix form (with
m
m'
H
):
¸
¸
¸
¹
·
¨
¨
¨
©
§
¸
¸
¸
¹
·
¨
¨
¨
©
§
¸
¸
¸
¸
¸
¸
¸
¹
·
¨
¨
¨
¨
¨
¨
¨
©
§
¸
¸
¸
¹
·
¨
¨
¨
©
§
0
'
1
422
2
'
20
20
'
2
1
2
1
3
2
1
3
2
1
ex
ex
T
T
mCR
T
T
T
R
R
R
R
mCR
T
T
T
dt
d
HHH
[8.24]
We will limit ourselves here to the discussion of solutions to the homogenous
system associated with [8.24] in the form
4
i
rt
e . By letting
'
2
R
R
a
and

Thermal Systems and Models 427
rmCR
/
, we obtain the non-dimensional eigenvalue equation (characteristic
equation):
>@
0844
422
20
20
2
///
/
/
/
aaaa
a
HH
H
[8.25]
The roots of equation [8.25] are:
3,2,
2
48164
;
22
1
r
/ / i
aaa
a
i
H
HHH
[8.26]
As the sum of the roots /
2
and /
3
of the equation are negative and their product
is positive, the two roots are negative (a diffusive system is aperiodic).
The symmetry of the system allows us to immediately find the modes. A
symmetric mode is characterized by
21
ii
4 4 . Substituting this relation into the
homogenous system derived from [8.24], we have:
1331
44;2
iiii
a 4 4/4 4/
H
Eliminating 4
i3
between these relations, we find that the eigenvalues /
i
corresponding to these modes satisfy the second order trinomial of characteristic
equation [8.25]. The values of 4
i1
and 4
i3
are of the same sign or of opposite sign
depending on whether
a/ is positive or negative. Substituting –a as the value of
/ in the preceding trinomial, we find that this takes on a negative value, which
shows that the value – a is situated between the roots of the trinomial. We can easily
derive from this that the quantity
a/ is positive for the largest root /
3
, whereas
it is negative for the other root /
2
. We can verify immediately that the root
a /
1
corresponds to the anti-symmetric mode
1211
4 4 and 0
13
4 .
+ + +
/
2
(
1
(
3
(
2
+ – 0
/
1
(
1
(
3
(
2
+ + –
/
3
(
1
(
3
(
2
Figure 8.9.
Structure of normal modes classed with increasing modulus of the eigenvalues
312
rrr
(decreasing time constants)

428 Fundamentals of Fluid Mechanics and Transport Phenomena
The structure of the modes is shown in Figure 8.9. The time constant of a mode
is equal to
r1 . The preceding discussion shows that we have
312
rrr . The
slowest mode corresponds to the root r
2
for which the three sub-systems at the same
temperature constitute a thermodynamic system in equilibrium, a structure for which
the thermal inertia is greatest towards the thermal resistances R’. On the other hand,
the most “agitated” mode corresponds to the smallest time constant
3
1 r .
Suppose now that the mass m’ of the sub-system E
3
is small compared to the
mass m of the sub-systems E
1
and E
2
(i.e.
H
<< 1). Performing a series development
of the roots [8.26], we obtain:
H
H
OaOa / / / 21
4
;
231
Returning to the dimensional values
mcRr
ii
/ , we obtain:
'
14
'
121
231
mCR
r
mCR
r
RRmC
r
¸
¸
¹
·
¨
¨
©
§
H
The values r
1
and r
2
are those already found ([8.22]) for the system studied in
section 8.3.1. As the value of r
3
is large compared to r
1
and r
2
, mode 3 is very
quickly damped; after this damping, we have the relation [8.19] for i =3, which can
here be written
0.
ˆ
3
4'
t
tX . Replacing
tX
ˆ
, ' (a matrix which allows us to
pass from [8.23] to [8.24]) and 4
3
by their values at small
H
:
¸
¸
¸
¹
·
¨
¨
¨
©
§
4
¸
¸
¸
¹
·
¨
¨
¨
©
§
'
¸
¸
¸
¹
·
¨
¨
¨
©
§
HH
/2
1
1
;
00
00
00
;
ˆ
3
3
2
1
mC
mC
mC
T
T
T
tX
we obtain:
02.
ˆ
3213
4' TTTmCtX
t
[8.27]
Relation [8.27] reduces to the balance equation of the sub-system E
3
(third
equation [8.23]) in which the mass is negligible. We verify that in replacing T
3
in
the first two equations of [8.23] with its value taken from [8.27] we recover
equations [8.21]: the three sub-systems model has been reduced to a model with two
sub-systems by removal of the third sub-system of small mass.
Thermal Systems and Models 429
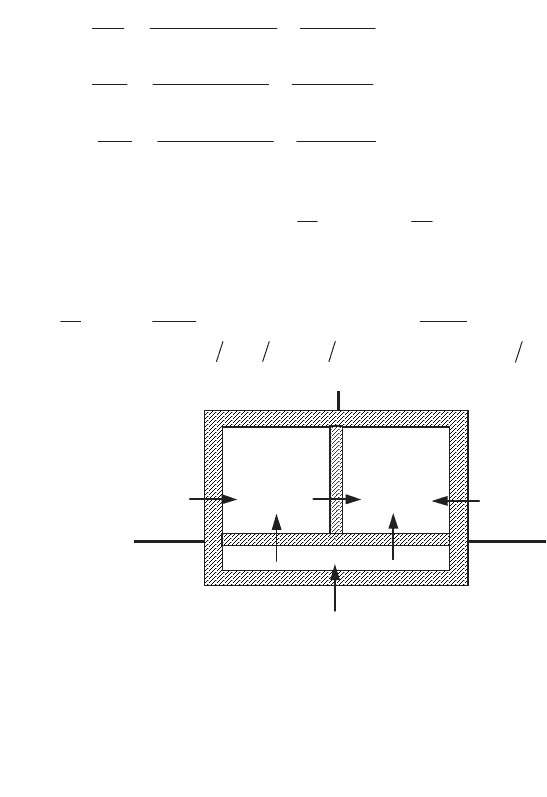
8.3.1.4. Thermal systems with 3 components in the form of a star
Now consider the system shown in Figure 8.10, which comprises three sub-
systems E
1
, E
2
and E
3
in contact two by two across the same thermal resistances R.
Each of these is in contact across the same thermal resistance R’ with the external
temperature medium T
i
ex
(t) (i = 1, 2, 3). We will only discuss the structure of the
modes here. The energy balance equations can be written:
'
2
'
'
2
;
'
2
333213
223212
113211
R
TT
R
TTT
dt
dT
Cm
R
TT
R
TTT
dt
dT
mC
R
TT
R
TTT
dt
dT
mC
ex
ex
ex
[8.28]
or, in matrix form, letting:
¸
¸
¹
·
¨
¨
©
§
'
2
R
R
a and
m
m'
H
:
¸
¸
¸
¹
·
¨
¨
¨
©
§
¸
¸
¸
¹
·
¨
¨
¨
©
§
¸
¸
¸
¹
·
¨
¨
¨
©
§
¸
¸
¸
¹
·
¨
¨
¨
©
§
HHHH
ex
ex
ex
T
T
T
mCR
T
T
T
a
a
a
mCR
T
T
T
dt
d
3
2
1
3
2
1
3
2
1
'
1
11
11
11
1
[8.29]
T
1ex
T
1
T
2
T
2
ex
M
2w
M
1w
M
1,2
M
3,2
M
3,1
M
3
w
T
3ex
T
3
E
1
E
2
E
3
R
R
R'
R'
R'
R
m'
m
m
Figure 8.10.
System with three sub-systems (second example)
Searching for solutions of the form 4
i
rt
e for the homogenous system associated
with [8.29] gives the non-dimensional eigenvalue equation, where we have let
rmCR / :

430 Fundamentals of Fluid Mechanics and Transport Phenomena
0
11
11
11
/
/
/
H
a
a
a
or:
0121221
2
223
/// aaaa
HHH
[8.30]
Taking account of the system symmetry, we see immediately that the anti-
symmetric mode verifies the relations
1211
4 4 and 0
13
4 . Substituting
these relations into the equations of the homogenous system, we find that the
corresponding eigenvalue is equal to
)1(
1
/ a . The characteristic equation
[8.30] can be written:
2
1 [ ( ( 1) ) ( 1)( 2)] 0a %%aaaa// / [8.31]
Its two other roots /
L
are (i = 2.3):
H
HHH
2
1421
2
222
aaaaaa
i
r
/
The structure of the modes can be obtained by simple reasoning. Taking account
of the system symmetry, the other eigenfunctions should present the symmetry
21 ii
4 4 . Substituting this relation into the homogenous system derived from
[8.29], we obtain:
1331
2;1
iiiiii
aa 4 4/4 4/
H
We immediately find that the values /
L
which satisfy the preceding relations are
the roots of the second order trinomial of characteristic equation [8.31]. The values
of 4
L
1
and 4
L
3
have the same sign or opposite sign depending on whether a
i
/
H
is positive or negative. Substituting
a
H
as the value of /
L
in the preceding
trinomial, we find that this takes on a negative value, showing that this value is
between the roots of the trinomial. The result is that the quantity
a
i
/
H
is
positive for the largest root /
3
, whereas it is negative for the other root /
2
. Figure
8.11 shows the structure of the three modes.
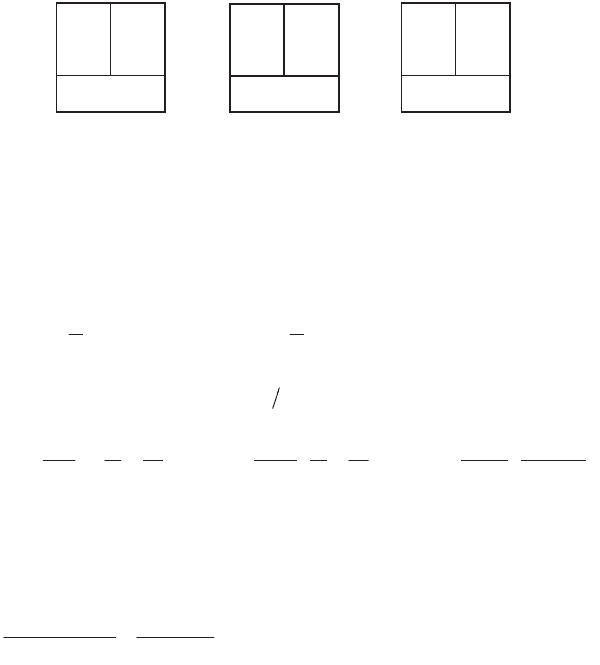
Thermal Systems and Models 431
+ –
0
/
1
= - a - 1
E
1
E
2
E
3
/
3
+ +
–
E
1
E
2
E
3
/
2
+ +
+
E
1
E
2
E
3
Figure 8.11.
Structure of normal modes
For small values of the calorific capacity m'C of sub-system E
3
, a development
in
H
gives the values:
H
H
O
a
aO
a
/ /
2
11
23
The corresponding values of
mCRr
ii
/ are:
¸
¸
¹
·
¨
¨
©
§
¸
¸
¹
·
¨
¨
©
§
¸
¸
¹
·
¨
¨
©
§
'2
'3
'
1
'
121
'
131
231
RR
RR
mCR
r
RRmC
r
RRmC
r
H
As in the case of three components in series, r
3
is much larger than r
1
and r
2
, and
mode 3 is thus rapidly damped. The third equation of system [8.28] can thus be
written:
0
'
2
33213
R
TT
R
TTT
ex
The reader can verify that the preceding relation is identical to condition [8.19].
Contrary to the case of three components in series, the limit of this system for m' = 0
is not the preceding system of two sub-systems (section 8.3.1.2).
8.3.2. Thermal models in continuous media
8.3.2.1. Overview
The idea of a continuous medium amounts to replacing an integer valued index
(number of components of the state vector X) by a spatial variable of continuous
values. The temporal and spatial behaviors of the system are thus continuous
functions or piecewise continuous. However, we have seen in Chapter 5 that the
theory of characteristics allows us to identify different behaviors for these variables.
If the time is by nature irreversible, the spatial properties or spatio-temporal
