Peube J-L. Fundamentals of fluid mechanics and transport phenomena

Подождите немного. Документ загружается.

Thermal Systems and Models 413

8.2.1.2.

Intensive variables and thermodynamic fluxes

We have seen that if the extensive variables of a system or a sub-system are

always defined, the same is not necessarily true of the intensive variables that only

have meaning if the system is in equilibrium. The complete

thermodynamic

representation

consists of representing the system with sufficient details, such that

each of the elementary sub-systems is close to a state of instantaneous equilibrium.

This condition is fulfilled if the size of the elements is not too great. For a finite sub-

system which is never rigorously in equilibrium, we have discussed the way to

define the mean intensive quantities (section 1.4.2.5 and section 6.5.2.4).

(a)

(b)

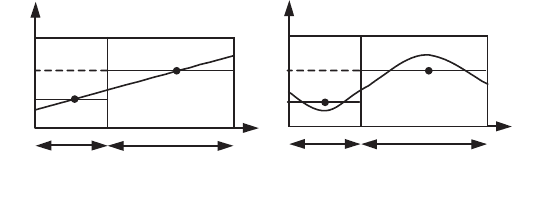
Figure 8.3.

Thermal flux between two neighboring elements

The behavior laws necessary to close the system of equations of the system

create a particular difficulty, as the thermodynamics fluxes which cross a surface are

related to the local gradients of the intensive quantities of the local continuous

medium. The problem is thus to express these by means of the intensive quantities

of the neighboring sub-systems. There is no general solution to this problem. Let us

take as an example the thermal resistance between two elements. Consider a fixed

1D continuous medium which is modeled as two blocks E

and E

which are

homogenous and of width

and

(Figure 8.3). For a fixed homogenous medium,

the mean temperatures

and

of each element are defined here by taking the

mean of the temperatures. Attributing the mean temperature to the central points of

the elements may appear natural. However, if the temperature gradient at the

interface is equal to the slope of the segment M

in the temperature distribution

of Figure 8.3a, the same is not necessarily so in the case of Figure 8.3b.

The segmentation of the continuous medium is acceptable for the thermal

imbalance of the first case, whereas it is too coarse for that of the second case. We

encounter here a usual interpolation problem.

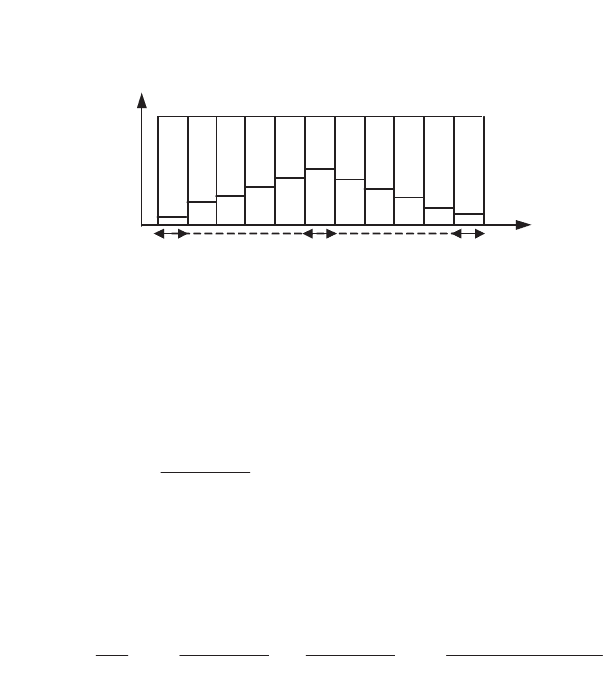
414 Fundamentals of Fluid Mechanics and Transport Phenomena

The modeling of thermal fluxes between the two sub-systems requires in

addition a

suitable

discretization

of the intensive quantities between two neighboring

sub-systems

. Let us consider two examples:

1) Consider a

1D solid

(Figure 8.4) subjected to a conductive thermal flux and

discretized into

elements E

of uniform thickness

and temperature

(i=1,2,…,n). The element E

is characterized either by its energy

or by its mean

temperature

CeTCdTQ

1

n-1

i-1

i+1

n-1

i+1

i-1

e e e

Figure 8.4.

Model of a 1D thermal transfer

We must now express the thermal fluxes between two neighboring elements.

Assuming that the middle of each element is at temperature

, we can write the

thermal flux

i,i+1

received by E

from E

i+1



iTi





We note that this expression satisfies the principal of action and reaction

(

1, 1,Ti i Ti i



 ) associated with the conservation of energy. If there is no lateral

thermal flux, the balance equation can be written for each element E



TTT

iiiiiiii 1111







OOOU

[8.3]

2) Consider the established flow of a fluid in a cylindrical pipe. We assume, in

order to simplify matters, that the flux and the physical properties of the fluid are

constant.

Thermal Systems and Models 415

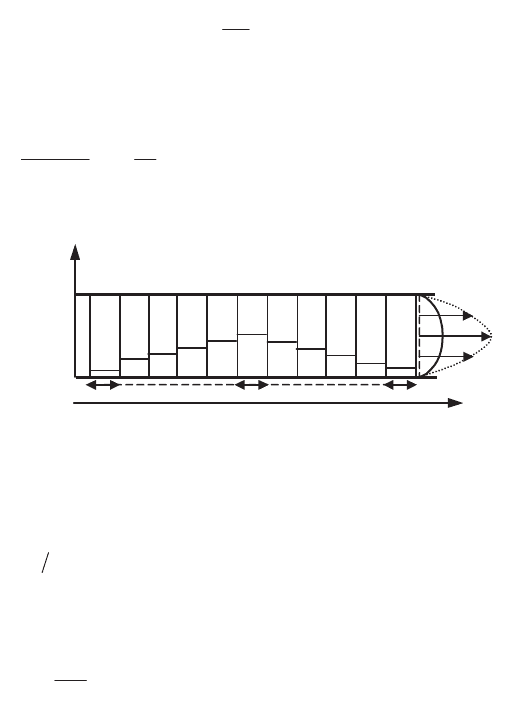
We have seen (section 6.5.2.2) that the balance equation of a quantity g in a pipe

can be written by means of surface integrals on a cross-section and an integral over

the contour of this section ([6.82]). We thus consider a cutting out of the pipe into n

surfaces S

with an inter-surface spacing of e (Figure 8.4). Let ),( Mtu and ),( MtT

be the velocity and temperature distributions in the cross-section; we define below

the mean temperature T

and the mean mixing-temperature T

for the section S

 

³³

Tdsu

tTTdstT

;

The energy balance in the pipe can be written ([6.87]):



³³³³





TpT

dqdsuCTds

n-1

i+1

i-1

n-1

i-1

i+1

Sn-1Si+1SiSi-1

e e e

u(t,M)

Figure 8.5.

Model of a pipe flow with thermal transfer

The calculation of the convective thermal flux between two successive surfaces

must be realized from upstream to downstream of the flow (section 5.6.1) and the

derivative

xww should be discretized between the sections S

i-1

and S

. Let T

be the

temperature of the wall associated with the surface S

; the preceding equation [6.87]

can thus be written:

 



mipiimimv

TTheTTCq

CSe  



FUU

[8.4]

where we denote by

F

the perimeter of the cross-section. The exchange coefficient h

between the fluid and the wall is defined as a function of the mean mixing-

temperature T

; its value depending on the considered problem is obtained from

experiments or theoretical evaluation in neighboring problems ([SCH 99], [YIH

77]).

416 Fundamentals of Fluid Mechanics and Transport Phenomena

8.2.1.3. Balance equations for the sub-systems

The writing of balance equations for a system is not necessarily associated with

the cutting out which is chosen in order to model the n disconnected sub-systems.

Each finite sub-system is characterized by the extensive quantity G which it contains

and the flux

which it receives from the neighboring sub-systems. The balance

equations for the extensive mass quantity g in a domain S can be written ([2.7]):



³³



GSG

dvgdv

VMU

The extensive quantity of a system is obviously the sum of the corresponding

extensive quantities of its sub-systems only if these are disjoint. For two such sub-

systems, such as S

and S

, we have:

³³³





2121 SSSS

gdvgdvgdv

UUU

alance equation S

balance equation S

alance equation S

balance equation (S

)

balance equation (S

)

alance equation S

balance equation (S

)





Figure 8.6.

Balance equations for three material adjacent sub-systems

The balances can be obtained for sub-systems which are partially over-lapped.

Figure 3.6 shows the case of three contiguous sub-systems S

, S

and S

: the sub-

system S

 S

overlaps S

, but it is possible to write the balance equations for the 3

disjoint sub-systems or for the three ensembles of sub-systems different two by two.

This manner of proceeding is nonetheless limited by the fact that the system of

equations obtained must be suitably enough conditioned (section 7.2.7.3), each

equation providing specific and sufficient information. The sum of the internal

fluxes exchanged between the sub-systems is zero (principle of action and reaction).

In the construction of models and numerical schemes we must be careful that this

property is ensured (conservative scheme).

Thermal Systems and Models 417

8.2.1.4. Coupling coefficients between two sub-systems

Consider a system comprising n sub-systems E

characterized by their extensive

quantities g

and their associated intensive energy quantities, or an equivalent (for

example, quantity of heat and temperature). Let us assume that two elements i and j

exchange a flux of the quantity g under the effect of a difference the intensive

quantity

yy 

. The flux





ijij

yy 

of the quantity x received from the element

j by the element i is opposed to the flux





jiji

yy 

of the quantity x received from

the element

i by the element j (action and reaction) and the positive coefficients

and

are equal. The balance equations of the quantity g for these two sub-systems

can be written:

 

!!!!  

jiji

ijij

;

or, by classing the terms:

!!!!  

iji

jij

;

Denoting by

U the group of sources of the quantity g

and defining the state

vectors

G and Y of the extensive quantities g

and the corresponding intensive

quantities

, the balance equations can be written in the general form:

UJYK



[8.5]

The matrix

J translates the importance in each element of the external

contributions. As the

coupling coefficients

and

between the elements i and j

are equal, the matrix K is symmetric. This feature is not a general constant, since the

coefficients of

are functions of the state variables of the elements i and j.

So, the extensive variable

and the intensive variable y

of a sub-system are

related by a state equation. Passage to the form [8.1] of the state representation of

the system can often be realized in thermal systems by expressing in each of the sub-

systems the

extensive variable g

as a function of the only corresponding intensive

variable y



iii

ygg

By defining the diagonal matrix

of positive elements



iiijij

dydgd

, we have in this case:

418 Fundamentals of Fluid Mechanics and Transport Phenomena

[8.6]

Letting

Y = X, system [8.5] can be written in the form [8.1]:

. :with.

JBKABUXA



' ' 

[8.7]

It is easy to verify that the matrix

KA .

1

' of equation [8.1] is not symmetric,

except if the value of each element d

is independent of the index i (identical sub-

systems). The reader can verify these considerations by means of the example in

section 8.3.1.3 by comparing equations [8.23] and [8.24] (or [8.28] and [8.29]). The

importance of this property for the linear case is discussed in section 8.2.2.2.

8.2.1.5.

Equivalence of inputs and initial conditions

Inhomogenous system [8.8] with impulse inputs, but with zero initial conditions,

can be reduced to a homogenous system with non-zero initial conditions. Let us

verify this point in an elementary manner using second order differential equation

[8.8] with zero initial conditions and having a Dirac distribution



at instant 0 as

the input:

      

000)(

 xxtctxtxatx



[8.8]

By integrating between 0 and a small time

and assuming that the functions

 

txandtx



remain bounded, we obtain:

 

oxcx )(



Problem [8.8] is thus reduced to a homogenous problem with an initial condition

at the instant

    

cxoxtxtxatx 



,;0)(

[8.9]

Letting

tend to zero, we obtain the equivalent problem [8.10]:

   

cxxtxtxatx  0,00;0)(



[8.10]

The mechanical interpretation of this result (sometimes known as Schwartz’s

theorem) is clear, given an initial velocity c is equivalent to the application of an

impulse which produces this velocity at the initial instant.

Thermal Systems and Models 419

The reader can verify in the same way that non-linear problem [8.11] is

equivalent to problem [8.12]:

   

00.)(.

 XtXtUBtXXA

[8.11]

  

0.)(. XXtUBtXXA

 [8.12]

We can replace the initial conditions with these additional impulse inputs which

act on the state variables. In certain cases, these can be realized by acting on the

existing inputs U, except if the number of state variables n is greater than the

number of independent inputs. In summary, it is often not possible to make clear

conceptual distinctions between inputs and initial conditions (or boundary

conditions) such that they appear in the mathematical representation of a model.

8.2.1.6.

Modeling and numerical solution of equations for continuous media

We have reasoned so far in the context of “thermodynamic” modeling of systems

by means of an ensemble of discrete sub-systems which are each in a state of

thermodynamic quasi-equilibrium. Other approaches are possible for obtaining

discretized equations from the balance equations for continuous media:

– finite difference methods consist of discretizing the domain under study and

replacing the differential operators at the points of the grid thus obtained with finite

difference operators;

– finite element methods represent the local solution by simple algebraic

functions in very small sub-domains; the balance equations are integrated in the

domain after multiplication by the weighting functions, n being the number of

unknown parameters defining the ensemble of local solutions. Integrations by parts

often allow the reduction of the order of the necessary derivatives, and the use of

finite elements of standard form allows the realization of very general calculatory

procedures. We thus obtain an integral formulation comprising n integral conditions

for the determination of n unknowns;

– finite volume methods consist of the definition of finite elements in which the

balance equations are integrated; the approximations of the solution in each element

are simple algebraic functions.

In all cases, we obtain a system of equations which is analogous to the state

representation, the preceding numerical schemes belong to two broad categories

depending on whether they are conservative or not (a numerical scheme is said to be

conservative if the discretized equations exactly satisfy the balance of an extensive

420 Fundamentals of Fluid Mechanics and Transport Phenomena

quantity with the variables which are used to represent the system). A conservative

scheme avoids the amplification of numerical errors which are integrated into the

balance of physical quantities. It cannot of course correct the unstable character of a

physical system. The finite element method is not conservative, contrary to the finite

volume method. Finite difference schemes may or may not be conservative. Finally,

it is important to remember that, regardless of the method used for discretizing the

equations, numerical schemes and algorithms used should respect the rules of

transmission of information from one point or element to another which results from

the character elliptic, hyperbolic, parabolic or mixed of the equations (section 5.6.1).

8.2.2. Linear time-invariant system (LTIS)

8.2.2.1. Introduction

Differential system [8.7] for A constant and with initial conditions can be

written:



0,.. XXUBXA

 [8.13]

The linearity of equation [8.13] makes it possible to use the usual methods of

solving linear differential equations. The solution is the sum:

– of a particular solution

)(tX

of the complete system [8.14]:

UBXA

..  [8.14]

– and a solution

)(

tX of the homogenous system [8.15] adjusted such that the

solution satisfies the initial conditions:

 

XXXXA

 [8.15]

The solutions of the homogenous system [8.15] are real decaying exponentials or

damped sinusoidal functions if the system is stable. They represent

transitional

regimes

A particular solution

)(tX

is often chosen so as not to contain transitional

terms and represents an

established regime of the problem treated (assumed stable),

independent of the initial conditions. This established regime plays a very important

role in numerous cases, in particular when the inputs are either simple algebraic

Thermal Systems and Models 421

functions of time or harmonic excitations. This particular solution can be obtained in

general by the variation of constants method (see mathematical texts).

The separation between transitional and established solutions is no longer

theoretically so clear for

non-linear systems; it can however be useful in numerous

cases, as dissipation phenomena are often associated with a progressive elimination

of the initial conditions, except of course in the case of a multiplicity of established

solutions (section 6.6.2).

The above result can be immediately transposed to partial differential equations.

In this case the particular solution



of the inhomogenous equation should

satisfy all the zero and non-zero boundary conditions, the solutions of the

homogenous equation satisfying zero boundary conditions. The solution obtained for

the homogenous equation is chosen such that the complete solution satisfies the

initial conditions.

8.2.2.2.

Recall on transitional regimes

The general solution of homogenous equation [8.15] is a linear combination of

terms of the form

4 ,

 being a solution of the eigenvalue problem:

  

0unitmatrix AI I/4 [8.16]

Equation [8.16] only has non-zero solutions for particular values

/

, which are

known as eigenvalues, of which there are

n, including their eventual multiplicity.

For each value

/

the solutions of equation [8.16] are of the form

c 4 , where 4

an eigenvector associated with the eigenvalue

/

is some constant). An

eigenvalue and its associated eigenvectors are known collectively as a mode. The

eigenvalues are real and negative for aperiodic modes (in thermal systems in

particular) or complex with a real part which may be negative for oscillatory damped

modes or zero for unamped modes (in acoustics for example). By limiting ourselves

here to thermal systems, the eigenvalues



can be written:

  

ttX

iii

/4 exp

The complete solution of a given problem is thus written:

     

/4 

iiie

tctXtXtXtX

exp

:with

[8.17]

The scalar coefficients

are calculated from the initial condition



0X which is

assumed to be known:

422 Fundamentals of Fluid Mechanics and Transport Phenomena

 

4

iie

cXX

00 [8.18]

The transitional regimes are solutions comprising the return to rest of the

homogenous system (or to the established regime

)(tX

of the system with a right-

hand side) from non-zero initial conditions (or eventually zero for an established

regime )(

). Having determined the eigenvectors 4

, the coefficients c

are

solutions of linear system [8.18], the matrix of which is full; for a large number

n of

equations this system is ill-conditioned (section 7.2.7.3). However, if a scalar

product exists

! VU for which the matrix A is self-adjoint

(

!!  VAUVUA ), the eigenvalues 4

are orthogonal (taking account of

[8.16], if

/z/

, we have 0

! 44/! 44/! 44



jijjiiji

AA ).

For the scalar product

UVVUVU

' ' of the vectors U and V , defined

with the diagonal matrix

(relation [8.6]), K being symmetric, this leads to:

! '' '' '! 



VAUKVUKVUVKUVAUVUA

tttttt 11

We can deduce from this, in a manner analogous to that outlined in section

A.4.2.2 of Appendix 4:

 

XXXXXc ..00 ''

NOTE

–

Expression [8.17] is the development at instant t of the function



t on

the basis of eigenfunctions

with instantaneous coefficients



exp

ct/ . After a

time lapse

t, which is large compared to 1//

, the mode j is no longer present in the

transitional solution; its coefficient there being equal to zero, this gives:

  

0..

4' 4'

tXtXtX [8.19]

8.3. Modeling linear invariant thermal systems

8.3.1. Modeling discrete systems

8.3.1.1. Introduction

The fundamental problem is the reasoned choice of the number of sub-systems

or the variables necessary for representation of a system, the number of variables