Poole Ch.P., Jr. Handbook of Superconductivity
Подождите немного. Документ загружается.


26 Chapter 1: Introduction
Type II superconductor Totally expels and excludes magnetic flux below
lower critical field Bcl and partially does so between Bcl and upper critical field
Bc2; all superconductors except elements are Type II.
Ultrasmall
Josephson junction
The junction size is smaller than typical weak
link.
Ultrasound absorption
Can provide the width of energy gap in classical
superconductors.
Ultraviolet (UV) Light beyond visible range in which the frequency is greater
than that of visible light.
Umklapp process three-phonon "flipping over" process involving nonzero
reciprocal lattice vector G (G - 0 for normal process); a mechanism for thermal
conductivity.
Upper critical field of
Type II superconductor Bc2 -Oo/2n~ 2.
USO Unconfirmed superconductivity observation.
Vacancy
Absence of atom at an atomic site.
Valence electron
Outer atomic electron, available for chemical bond.
Van der Waals force Relatively weak force between molecules arising from
shifts in their electric charge distributions.
Van
Hove singularity Associated with flat energy bands and peak in density of
states.
Villars-Phillips model Provides structural and atomic criteria for presence of
high T c.
Vortex Cylinder or tube of magnetic flux containing one quantum of flux Oo;
found in Type II superconductor located in magnetic field Bapp.
Vortex fluid Array of vortices capable of motion because of lack of sufficient
pinning.
Vortex glass State intermediate between flux liquid and flux solid.
Vortex lattice Regular arrangement of vortices, usually in a hexagonal pattem,
sometimes called Abrikosov lattice.
Wannier functions W(r- R); summations of normalized Bloch wave func-
tions over all the k-states of a band.
Weak coupled BCS Small electron-phonon coupling constant, 2 << 1.
Weak link Intermediate case between thick barrier connecting superconductors
that prevents interactions and thin barrier with strong coupling.
Weak pinning Vortex pinning force is less than Lorentz force
Wiedermann-Franz law Thermal to electrical conductivity ratio
Kth/aT = 3kg/2e 2.
Woodstock of Physics
"Special Panel Discussion on Novel High Temperature
Superconductivity" held at the March 1987 New York meeting of the American
Physical Society. It introduced high-T c to the world.
Work function Minimum energy needed to remove an electron from the
interior of a solid.
XAFS X-ray absorption fine structure.
XANES X-ray absorption near edge structure.

References 27
XAS X-ray absorption spectroscopy.
XPS X-ray photoemission spectroscopy.
Zeeman splitting Splitting of spectral line in a magnetic field.
Zero field cooling (ZFC) Cooling superconductor below its transition tempera-
ture in the absence of an applied magnetic field.
References
E J. Owens and C. P. Poole, Jr.,
The New Superconductors,
Plenum Press, New York, 1996.
C. E Poole, Jr., H. A. Farach, and R. J. Creswick,
Superconductivity,
Academic Press, New York, 1995.
C. P. Poole, Jr., T. Datta and H. A. Farach,
Copper Oxide Superconductors,
Wiley, NY, 1988.
This Page Intentionally Left Blank

Chapter 2
Properties of the Normal
M etallic State
Charles P. Poole, Jr.
Department of Physics and Institute of Superconductivity,
University of South Carolina, Columbia, South Carolina
A. Introduction 29
B. Conduction Electron Transport 30
C. Frequency-Dependent Electrical Conductivity 33
D. Brillouin Zones 34
E. Fermi Surface 36
F. Electromagnetic Fields 39
References 40
A
Introduction
The present chapter fumishes background on normal conductors, which provides
some perspective on the superconducting state. Material in this chapter consti-
tutes a convenient source for key definitions and formulas referred to later in the
Handbook. A standard solid-state physics text such as those by Kittel (1996) and
by Ashcroft and Mermin (1976) should be consulted for more details on these
ISBN: 0-12-561460-8 HANDBOOK OF SUPERCONDUCTIVITY
$30.00 Copyright 9 2000 by Academic Press.
All fights of reproduction in any form reserved.
29

30 Chapter 2: Properties of the Normal Metallic State
normal state properties. Our earlier works
Superconductivity
(1995) and
The
Physics Handbook
(1998) also supplement this material.
Conduction Electron Transport
The number density n (electrons/cm 3) of conduction electrons in a metallic
element such as copper or aluminum of density Pm (g/cm3), atomic mass number
A (g/mole), and valence Z is given by
n = NAZPm/A, (1)
where N A is Avogadro's number. Table 2.1 lists the electron densities of several
metals, and we see that they are a thousand times greater than the density of an
ideal gas at standard temperature and pressure.
A potential difference applied along a conducting wire produces an electric
field E and hence the force F =-eE
= m(dv/dt),
which accelerates the elec-
trons. They undergo successive periods of acceleration interrupted by collisions,
and during the average time z between collisions they attain a component of
velocity along the field direction,
Vav =
-(eE/m)~,
(2)
which is called the drift velocity, The negative sign means that the electrons move
in a direction opposite to that of the electric field.
The current density J,
J -- neVav,
(3)
can be written, with the aid of Eq. (2), in the form
J -- (neZ'c/m)E = %E,
(4)
and we have for the dc electrical conductivity % and its reciprocal the
resistivity p
cr o = ne2"c/m = 1/p.
(5)
The drift velocity Vav is much less than the Fermi velocity
v v
at which the
conduction electrons actually move on the Fermi surface. The mean free path l,
or average distance traveled between collisions, is given by
l = vvr. (6)
Typically, v v ~ 106 m/s for good conductors (i.e., 1/300 the speed of light) and it
is perhaps one-tenth of this value for A-15 compounds and high-temperature
superconductors in their normal states.
B. Conduction Electron Transport 31
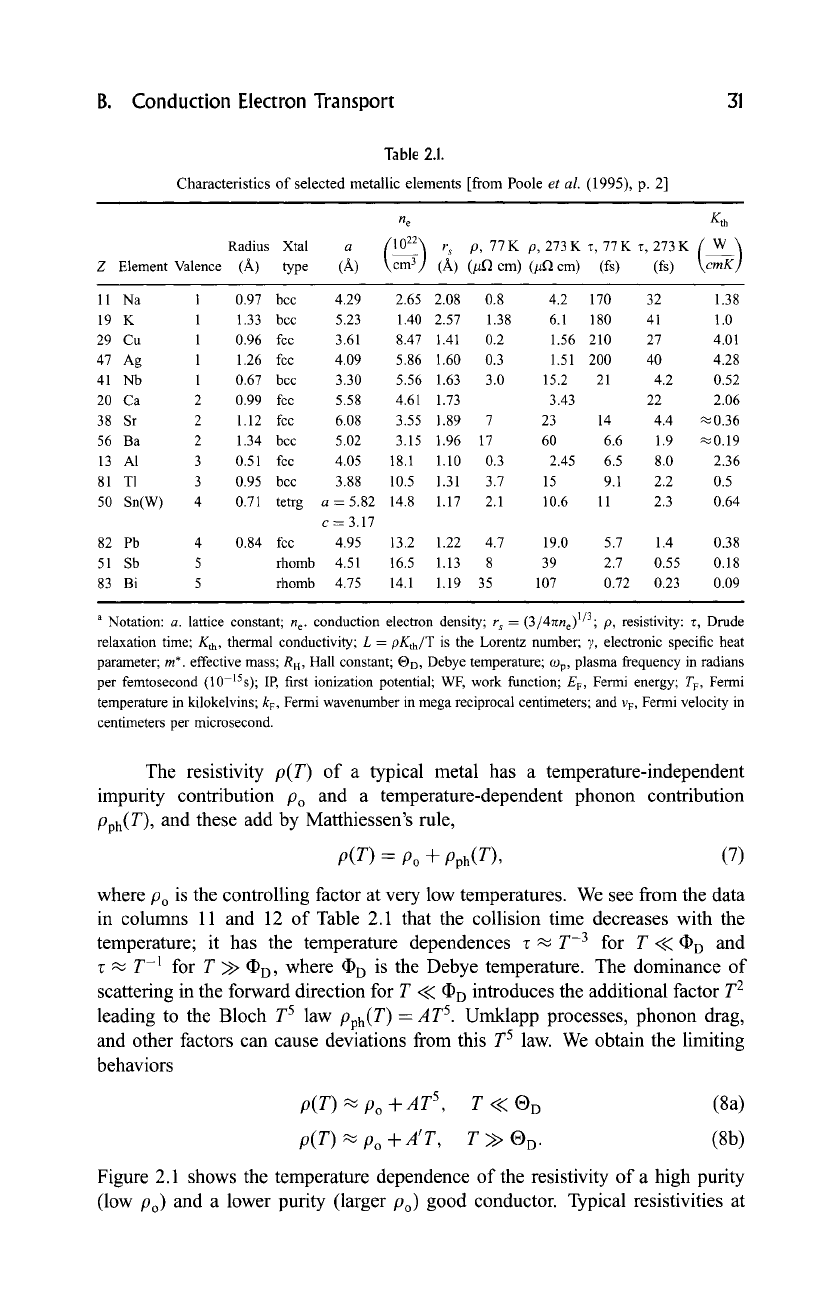
Table 2.1.
Characteristics of selected metallic elements [from Poole
et al.
(1995), p. 2]
n e
Radius Xtal
a
(1022) r s p, 77K p, 273K z, 77K r, 273K
Z Element Valence (A) type (A) \~m-~m 3 ] (A) (#f~ cm) (#f2 cm) (fs) (fs)
Kth
(w)
11 Na 1 0.97 bcc 4.29 2.65 2.08 0.8 4.2 170 32
19 K 1 1.33 bcc 5.23 1.40 2.57 1.38 6.1 180 41
29 Cu 1 0.96 fcc 3.61 8.47 1.41 0.2 1.56 210 27
47 Ag 1 1.26 fcc 4.09 5.86 1.60 0.3 1.51 200 40
41 Nb 1 0.67 bcc 3.30 5.56 1.63 3.0 15.2 21 4.2
20 Ca 2 0.99 fcc 5.58 4.61 1.73 3.43 22
38 Sr 2 1.12 fcc 6.08 3.55 1.89 7 23 14 4.4
56 Ba 2 1.34 bcc 5.02 3.15 1.96 17 60 6.6 1.9
13 A1 3 0.51 fcc 4.05 18.1 1.10 0.3 2.45 6.5 8.0
81 T1 3 0.95 bcc 3.88 10.5 1.31 3.7 15 9.1 2.2
50 Sn(W) 4 0.71 tetrg a = 5.82 14.8 1.17 2.1 10.6 11 2.3
c=3.17
82 Pb 4 0.84 fcc 4.95 13.2 1.22 4.7 19.0 5.7 1.4
51 Sb 5 rhomb 4.51 16.5 1.13 8 39 2.7 0.55
83 Bi 5 rhomb 4.75 14.1 1.19 35 107 0.72 0.23
1.38
1.0
4.01
4.28
0.52
2.06
~0.36
~0.19
2.36
0.5
0.64
0.38
0.18
0.09
a
Notation: a. lattice constant; n e. conduction electron density;
r s = (3~4tOne)l~3; p,
resistivity: ~, Drude
relaxation time; Kth, thermal conductivity; L =
pKth/T
is the Lorentz number; 7, electronic specific heat
parameter; m*. effective mass; R H, Hall constant; | Debye temperature; %, plasma frequency in radians
per femtosecond (10-15s); IP, first ionization potential; WF, work function;
Ev,
Fermi energy; T F, Fermi
temperature in kilokelvins;
k v,
Fermi wavenumber in mega reciprocal centimeters; and
vv,
Fermi velocity in
centimeters per microsecond.
The resistivity p(T) of a typical metal has a temperature-independent
impurity contribution Po and a temperature-dependent phonon contribution
Pph(T), and these add by Matthiessen's rule,
/9(T) =/90 -3 t-/gph(T), (7)
where Po is the controlling factor at very low temperatures. We see from the data
in columns 11 and 12 of Table 2.1 that the collision time decreases with the
temperature; it has the temperature dependences r ~ T -3 for T << ~D and
~ T -1 for T >> ~D, where ~D is the Debye temperature. The dominance of
scattering in the forward direction for T << ~i~ introduces the additional factor T 2
leading to the Bloch T 5 law Pph(T)- AT 5. Umklapp processes, phonon drag,
and other factors can cause deviations from this T 5 law. We obtain the limiting
behaviors
p(T) ,~ Po + ATS, T
<< O D
(8a)
p(T) ~ Po
+
A'T, T >> O o. (8b)
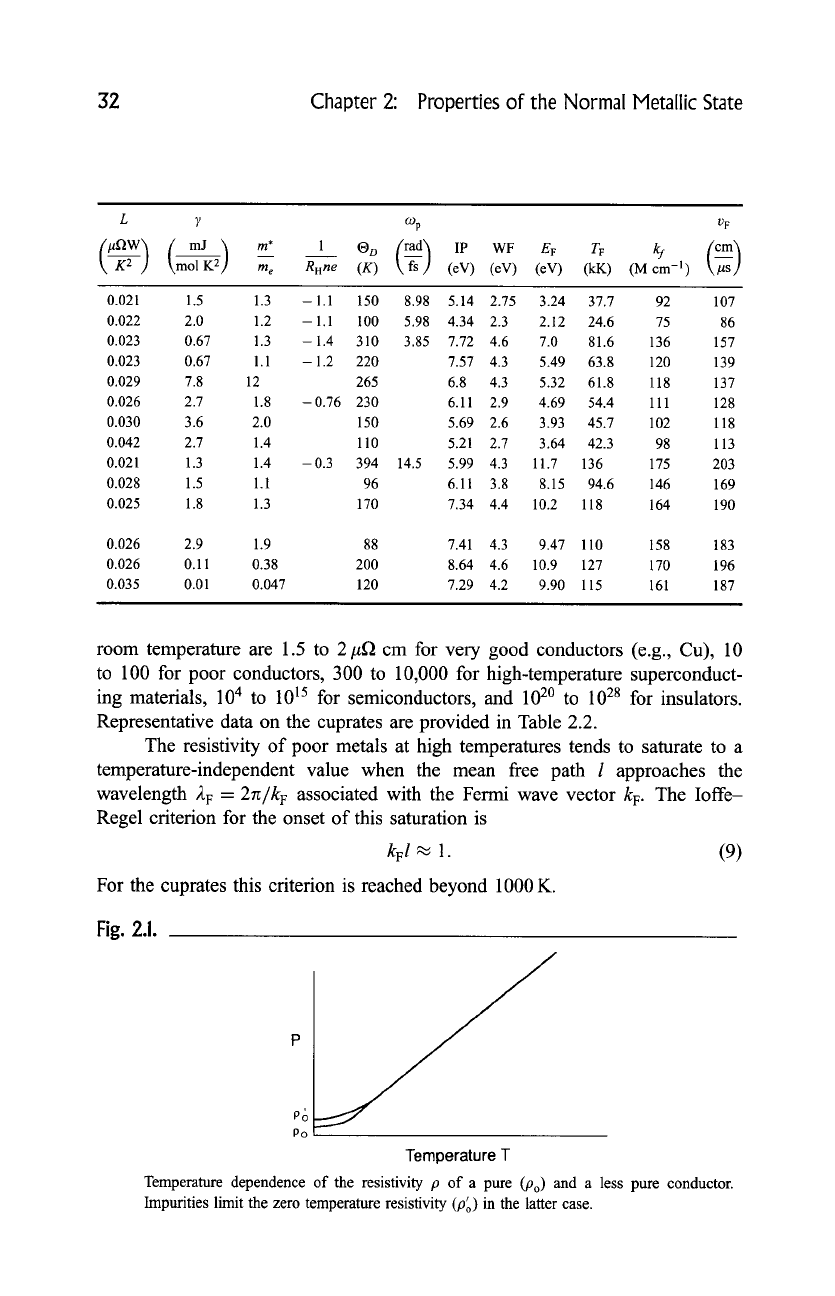
Figure 2.1 shows the temperature dependence of the resistivity of a high purity
(low Po) and a lower purity (larger Po) good conductor. Typical resistivities at
32 Chapter 2: Properties of the Normal Metallic State
L 7
(/~DW'~ ( mJ ) m*
,] mol K 2 m--~
COp O F
1 |
(tad)IP WF EF TF
kf
{cm)
Rune
(K) \ fs~/ (eV) (eV) (eV) (kK) (M cm -1) k ,]-~
0.021 1.5 1.3
0.022 2.0 1.2
0.023 0.67 1.3
0.023 0.67 1.1
0.029 7.8 12
0.026 2.7 1.8
0.030 3.6 2.0
0.042 2.7 1.4
0.021 1.3 1.4
0.028 1.5 1.1
0.025 1.8 1.3
0.026 2.9 1.9
0.026 0.11 0.38
0.035 0.01 0.047
- 1.1 150 8.98 5.14 2.75 3.24 37.7 92 107
-
1.1 100 5.98 4.34 2.3 2.12 24.6 75 86
- 1.4 310 3.85 7.72 4.6 7.0 81.6 136 157
- 1.2 220 7.57 4.3 5.49 63.8 120 139
265 6.8 4.3 5.32 61.8 118 137
-0.76 230 6.11 2.9 4.69 54.4 111 128
150 5.69 2.6 3.93 45.7 102 118
110 5.21 2.7 3.64 42.3 98 113
-0.3 394 14.5 5.99 4.3 11.7 136 175 203
96 6.11 3.8 8.15 94.6 146 169
170 7.34 4.4 10.2 118 164 190
88 7.41 4.3 9.47 110 158 183
200 8.64 4.6 10.9 127 170 196
120 7.29 4.2 9.90 115 161 187
room temperature are 1.5 to 2/~D cm for very good conductors (e.g., Cu), 10
to 100 for poor conductors, 300 to 10,000 for high-temperature superconduct-
ing materials, 104 to 1015 for semiconductors, and 1020 to 1028 for insulators.
Representative data on the cuprates are provided in Table 2.2.
The resistivity of poor metals at high temperatures tends to saturate to a
temperature-independent value when the mean free path l approaches the
wavelength 2F =
2rC/kF
associated with the Fermi wave vector
kF.
The Ioffe-
Regel criterion for the onset of this saturation is
kFl
~ 1. (9)
For the cuprates this criterion is reached beyond 1000 K.
Fig. 2.1.
P
po
po
Temperature T
Temperature dependence of the resistivity p of a pure (Po) and a less pure conductor.
Impurities limit the zero temperature resistivity (p~,) in the latter case.
C. Frequency-Dependent Electrical Conductivity
33
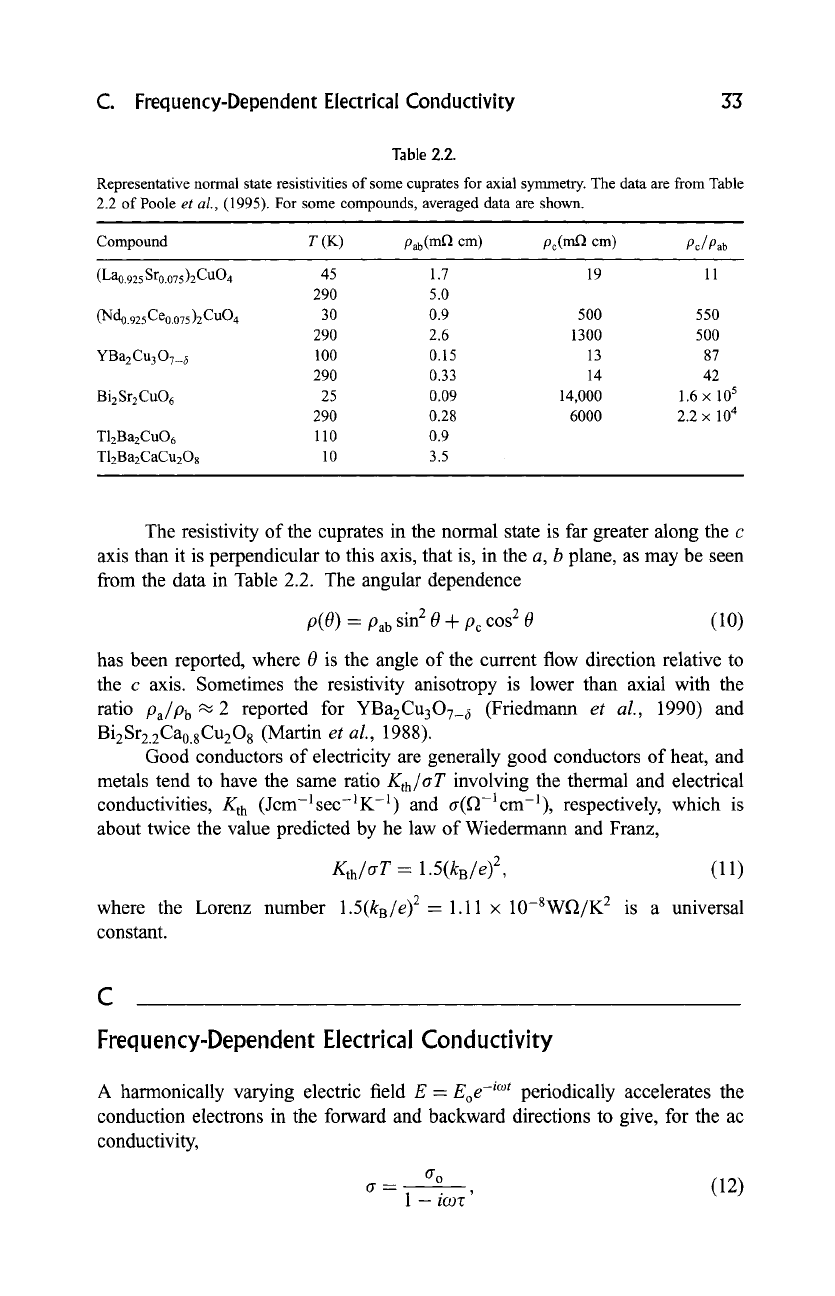
Table 2.2.
Representative normal state resistivities of some cuprates for axial symmetry. The data are from Table
2.2 of Poole
et al.,
(1995). For some compounds, averaged data are shown.
Compound T (K) Pab(m~ cm) pc(m.Q cm)
Pc/Pab
(La0.925 Sr0.075)2 CuO 4
45 1.7 19 11
290 5.0
(Nd0.925 Ceo.075)2CuO4
30 0.9 500 550
290 2.6 1300 500
YBa2 Cu3 07-6 100 0.15 13 87
290 0.33 14 42
BizSr2CuO 6 25 0.09 14,000 1.6 x 105
290 0.28 6000 2.2 x 104
TlzBa2CuO6 110 0.9
TlzBa2CaCu208 10 3.5
The resistivity of the cuprates in the normal state is far greater along the c
axis than it is perpendicular to this axis, that is, in the a, b plane, as may be seen
from the data in Table 2.2. The angular dependence
p(O)
= Pab
sin2 0 + Pc
cOS2 0 (10)
has been reported, where 0 is the angle of the current flow direction relative to
the c axis. Sometimes the resistivity anisotropy is lower than axial with the
ratio
Pa/Pb
~ 2 reported for YBa2Cu307_ 6 (Friedmann
et al.,
1990) and
BizSr2.zCa0.gCu208 (Martin
et al.,
1988).
Good conductors of electricity are generally good conductors of heat, and
metals tend to have the same ratio
Kth/aT
involving the thermal and electrical
conductivities, Kth (Jcm-1 see-1 K-1) and a(~-1 cm-1), respectively, which is
about twice the value predicted by he law of Wiedermann and Franz,
Kth/CYT = 1.5(kB/e) 2,
(11)
where the Lorenz number
1.5(kB/e)2=
1.11 • 10-8W~/K 2 is a universal
constant.
C
Frequency-Dependent Electrical Conductivity
A harmonically varying electric field E =
Eo e-i~
periodically accelerates the
conduction electrons in the forward and backward directions to give, for the ac
conductivity,
O" o
- ~, (12)
1 - iwz

34 Chapter 2: Properties of the Normal Metallic State
which reduces to Eq. (5) when the frequency is zero. When coz << 1, many
collisions occur during each cycle of the E field, and the average electron motion
follows the oscillations. When coz >> 1, then E oscillates more rapidly than
collisions occur, the electrical conductivity becomes predominantly imaginary,
corresponding to a reactive impedance, and the high-frequency dielectric constant
e(co) becomes
(13)
0)27 '
where COp is the plasma frequency,
O~p - (ne2/%m) 1/2,
(14)
and ,~p =
27zc/Ogp
is the plasma wavelength. For frequencies o~ < O~p the dielec-
tric constant is negative so electromagnetic waves cannot propagate, and above
this value E is positive and propagation occurs. This causes metals to be opaque
for co < COp and transparent for o~ > cop. The quantity ~p varies between 200 and
440 nm for the alkali metals.
D
Brillouin Zones
The positions of the atoms in crystals are expressed in ordinary direct lattice
coordinates x, y, z, and the energy bands of conductors and superconductors are
expressed in reciprocal space coordinates
kx, ky, k z,
sometimes called momentum
space. The reciprocal space basis vectors A, B, and C are related to their
coordinate space counterparts a, b, and c as follows:
2rib x c 2he x a 2ha x b
A -
B -- C = . (15)
a. (b x c)' a. (b x c)' a. (b x c)
When a, b, and c are orthogonal to each other, they are inverse in magnitude and
parallel in direction to their counterparts A, B, and C in k-space:
A = 2n/a, B = 2n/b, C = 2n/c.
(16)
For orthorhombic structures (a < b < c) the A > B > C are all different lengths;
for tetragonal crystals (a = b r c) we have A -- B :~ C, and for the cubic case
(a = b = c) the reciprocal space basis vectors A = B = C are all equal in
length. The unit cell in reciprocal space, called the (first) Brillouin zone BZ,
has the volume
ABC
= (2n) 3/abc for the orthogonal case.
Figure 2.2 sketches the Brillouin zone of the orthorhombic YBa2Cu307
structure which is not body-centered. The mercury high-temperature supercon-
ductors have the same type of Brillouin zone, with the dimensions given in Table

D. Brillouin Zones 35
Fig. 2.2.
Sketch of the Brillouin zone of orthorhombic YBa2Cu307 with the symmetry points
indicated. [Krakauer
et al.,
1988.]
Table 2.3.
Dimensions of the unit cell (a, b, c, in nm) and Brillouin zone (A, B, C, in nm -1) of four non-body
centered cuprates
Compound a b c A B C
YBazCu307_ 6 3.82 3.88 11.7 1.64 1.62 0.537
HgB a2CuO4 3.88 3.88 9.53 1.62 1.62. 0.659
HgBazCaCu206 3.86 3.86 12.66 1.63 1.63 0.496
HgBazCazCu308 3.85 3.85 15.78 1.63 1.63 0.398
2.3. We see from the table that the space unit cells of these four compounds are
elongated along c, and their Brillouin zones are compressed along C.
Figure 2.3 shows the Brillouin zone of La2CuO 4, which is body-centered,
and Fig. 2.4 shows how two adjacent La2CuO 4 unit cells fit together. The
thallium and bismuth compounds have the same types of Brillouin zones, but
compressed in the
k z
direction since their real space unit cells have about the same
a and b values, and much larger c values (hence smaller C values) than La2CuO 4.
Fig. 2.3.
Brillouin zone of body centered tetragonal La2CuO4 with the symmetry points indicated. The
symbols A and U designate general points along [110] directions. [Adapted from Pickett,
1989.]
