Poole Ch.P., Jr. Handbook of Superconductivity

Подождите немного. Документ загружается.

Chapter 3: Superconducting State

Hin --

-M, and the B field is zero. Near the surface the fields and current exist,

and they have the following values inside (0 < r < R):

Bin(r ) ~ B o

exp[-(R - 0/2]

(7)

Hin -H o (8)

M(r) ,~

-Ho[1 - exp(R -

r)/2]

(9)

Jsh(r) ~ -Jo

exp[-(R -

r)/2].

(10)

These values are plotted in Fig. 3.3, where

Bo - #o2J o (11)

The vectors Bin and Jsh- V x M are perpendicular to each other, and Bin(r )

satisfies the expression

Bin(r ) -

#o[Ho+M(r)]

(12)

where

M(r)

is negative everywhere inside. The superconducting medium can be

considered as reacting to the presence of the applied field by generating (a)

shielding currents Jsh that cancel the interior B field, or (b) a magnetization M that

nullifies the interior field Bin through Eq. (12), where Jsh -- V x M.

When transport current is caused to flow longitudinally along a Type I

superconducting wire in the absence of an applied field, it flows in a surface layer

of thickness 2 with the radial distance dependence given by Eq. (10). This

applied current induces magnetic field lines that encircle the wire outside and an

Fig. 3.3

B,,p.

-r"

-Bapp

~l, oHin B~op =

in? ~

1 !

89 R

Plot of the fields B and H and of the magnetization #o M inside (r < R) and outside (r > R)

a Type I superconducting cylinder of radius R in an axial applied magnetic field Bap p =

/~oHo . [From Poole

et al.

(1995), p. 42.]

Temperature

Dependencies

internal field

Bin

confined to the surface layer with the distance dependence of

Eq. (7).

There is really no fundamental difference between transport current and

shielding current. Current impressed from outside into a superconductor is called

transport current, and it induces an encircling magnetic field. When an external

magnetic field penetrates a superconductor, it is accompanied by induced

encircling shielding currents.

Temperature

Dependencies

The critical field and critical current density are related through the expression

Bc(T ) =

#o2(T)Jc(T),

(13)

where all three quantities are temperature dependent. At absolute zero we use the

notation Bc(0 ) = Bc, etc., and Eq. (13) becomes, in analogy with Eq. (11),

Bc = #oRJ c . (14)

A particular superconducting wire of radius R has a maximum current called the

critical current Ic, and for a Type I superconductor it has the value

I c = 2rcR2J c = 2~zRBc/#o.

(15)

The destruction of the superconducting state by exceeding the critical (transport)

current I c is called the Silsbee effect.

The penetration depth 2(T) is related to the super electron density ns(T )

through the expression

2(T) = 2L(T) =

[m/laons(T)e2] 1/2,

(16)

due to London. In the two-fluid model we have the temperature-dependent

expression for the super n s and normal nn, electron densities, respectively,

ns(T ) + nn(T ) = n,

(17)

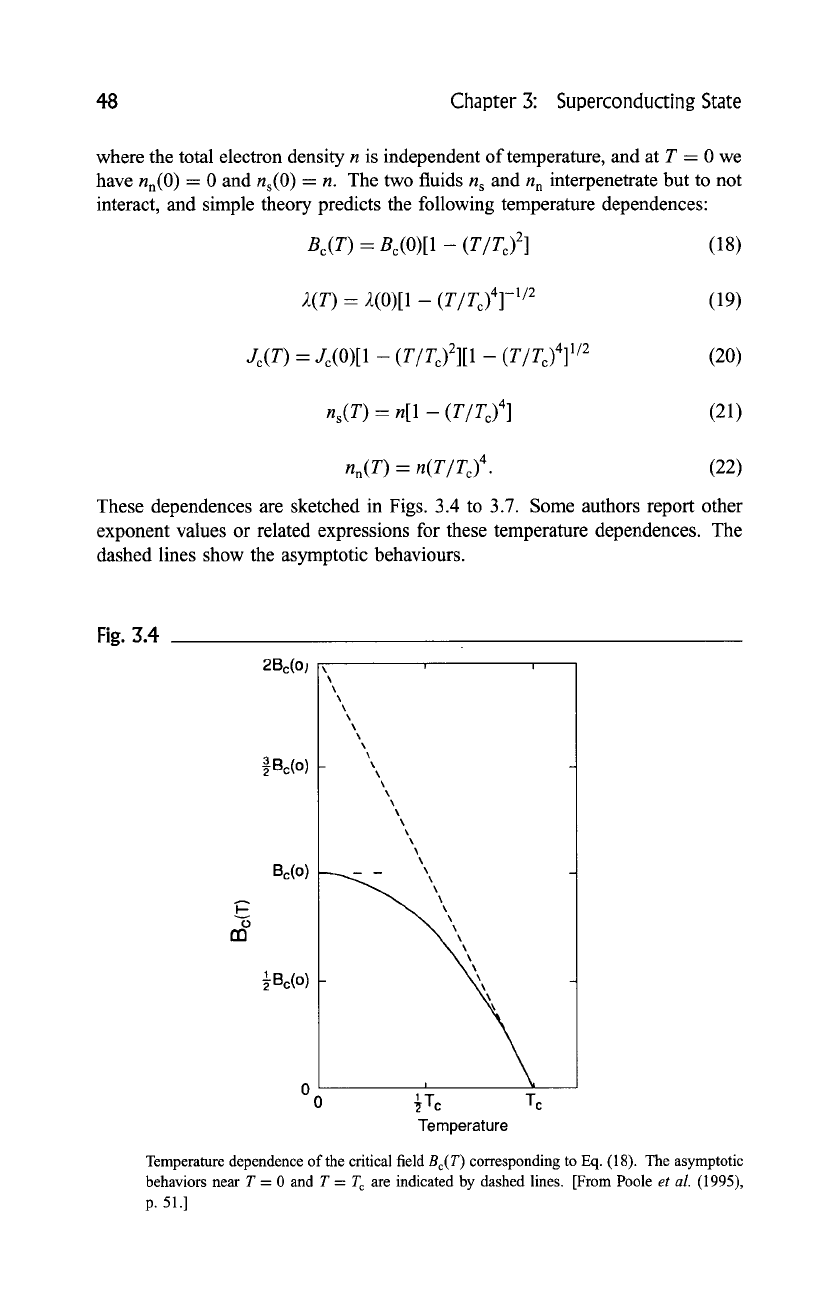
48 Chapter 3: Superconducting State

where the total electron density n is independent of temperature, and at T -- 0 we

have nn(0 ) -- 0 and ns(0 ) - n. The two fluids n s and n n interpenetrate but to not

interact, and simple theory predicts the following temperature dependences:

Bc(T ) - Bc(0)[1

(T/Tc) 2]

(18)

i(T) - I(0)[1

(T/Tc)4] -1/2

(19)

Jc(T) - Jc(0)[1

(T/Tc)2][1

(T/Tc)4] 1/2

(20)

ns(T ) - nil

(T/Tc) 4]

(21)

nn(T ) -

n(T/Tc) 4.

(22)

These dependences are sketched in Figs. 3.4 to 3.7. Some authors report other

exponent values or related expressions for these temperature dependences. The

dashed lines show the asymptotic behaviours.

Fig. 3.4

I--

2Bc(O/

23-Bc(o)

Bc(o)

89

\\\\\

),,

~\\

89 Tc

Temperature

Temperature dependence of the critical field Bc(T ) corresponding to Eq. (18). The asymptotic

behaviors near T = 0 and T = T c are indicated by dashed lines. [From Poole

et al. (1995),

p. 51.1

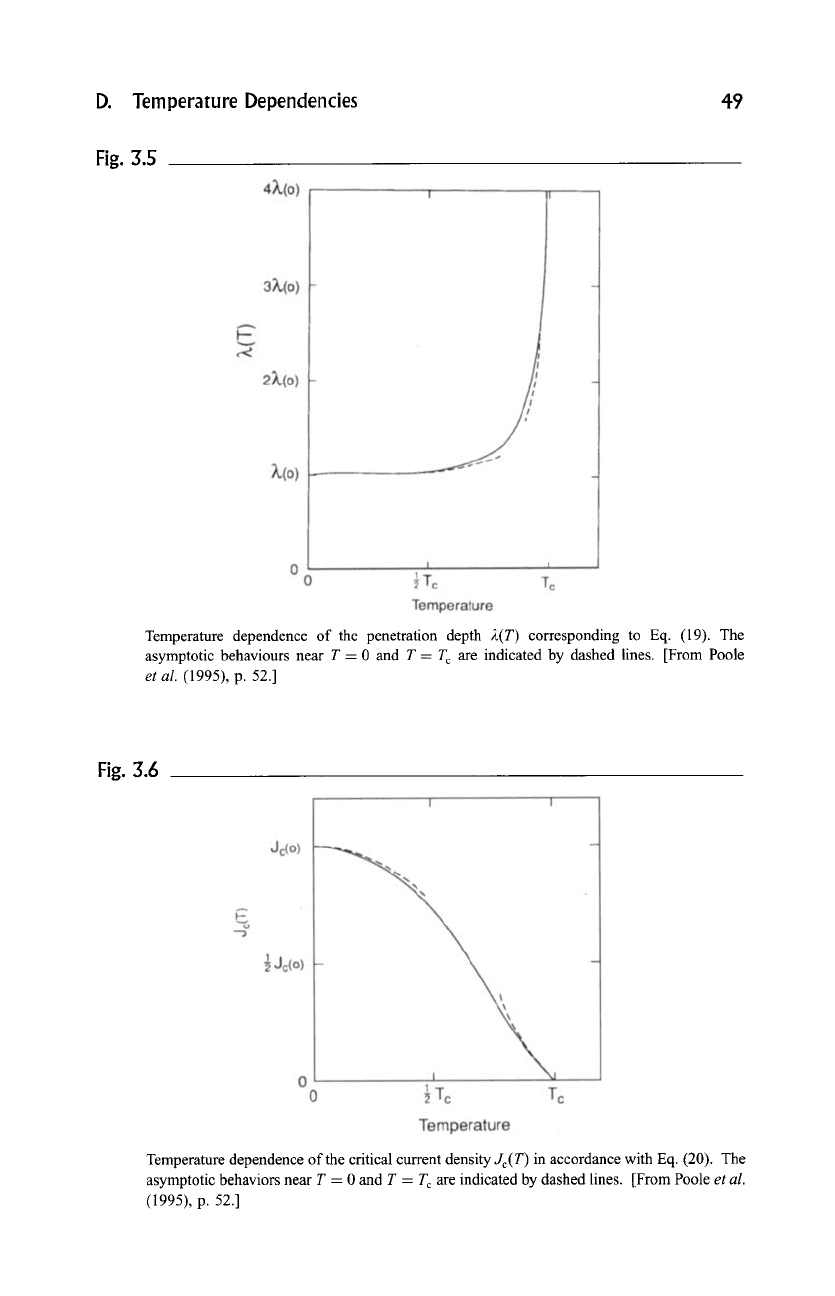
D. Temperature Dependencies 49

Fig. 3.5

Temperature dependence of the penetration depth 2(T) corresponding to Eq. (19). The

asymptotic behaviours near T = 0 and T = T c are indicated by dashed lines. [From Poole

et al.

(1995), p. 52.]

Fig. 3.6

Temperature dependence of the critical current density

Jc(T)

in accordance with Eq. (20). The

asymptotic behaviors near T -- 0 and T = T c are indicated by dashed lines. [From Poole

et al.

(1995), p. 52.]

Chapter 3: Superconducting State

Fig. 3.7

I-

n,(o)

' n,(o)

I " !

89 rc

Temperature

Temperature dependence of density of superconducting electrons n s as given by Eq. (21). The

dashed lines indicate the slopes

dns/dT=O

at T-0, and

dns/dT=-4n/T c

T = T c. [From Poole

et al.

(1995), p. 53.]

The temperature dependencies of Eqs. (18) and (20), respectively, permit us

to define a critical surface in the three-dimensional space of applied magnetic

field

Bapp,

applied transport current Jxr, and temperature T, and this is sketched in

Fig. 3.8. This surface constitutes the boundary between the normal and super-

conducting regions, so the material is superconducting for points (Bapp, JTr, T)

that lie below it and normal for points above it.

Fig. 3.8

T/TCai

b i

c k -" h

JTr / Jc(o)

Bap p / Bc(o)

Critical surface of a superconductor. Values of applied field Bapp, transport current

JTr

and

temperature T corresponding to points below the critical surface are in the superconducting

region, and points above this surface are in the normal region. [From Poole

et al.

(1995),

p. 54.]

E. Critical Magnetic Field Slope 51

Fig. 3.9

1.0

0.5

I 1

0 0.5 1.0

T/'I' c

Temperature dependence of the BCS energy gap A(T) normalized relative to the zero

temperature gap A(0) as given by Eq. (23), where

A(T)=

89 [From Poole

et al.

(1995), p. 167.]

The superconducting energy gap Eg(T) -- 2A(T) in the neighborhood of T c

has the simple theory temperature dependence:

Eg(T) ,~ 3.53 kBTc[1-

(T/Tc)] 1/2,

(23)

sketched in Fig. 3.9 where A(0) = 1.76 kBTc.

The temperature dependences of the various quantities presented in this

section are predicted by simple theoretical approaches to superconductivity and

are sometimes reasonable approximations to experimentally measured values.

These expressions all assume an isotropic material.

Critical Magnetic Field Slope

The critical magnetic field has the parabolic dependence on the temperature given

by Eq. (18), with the following slope near T c"

dBc(T) 2Bc(T)

dT T c

(24)

Chapter 3: Superconducting

State

For typical Type I superconductors this slope varies between -15 and

-50mT/K. A Type II superconductor has lower Bcl and upper Bc2 critical

fields, and typical values of their slopes for a cuprate are

dBcl

2Bcl(0)

dT Tc

~ - 1 mT/K (25)

dBc2

2Bc2(0)

= -~ ~ -1.83 T/K. (26)

dT T c

The latter slope of- 1.83 T/K comes from the Pauli limiting field approximation

Bpaul i --Eg/2~/'2#B-

1.83 T c, (27)

obtained by using the BCS expression Eg - 3.53k B T c. The slopes of Eqs. (25)

and (26) near T c can be quite anisotropic for high-temperature superconductors.

References

D. B. Haviland, Y. Liu and A. M. Goldman,

Phys. Rev. Lett.

62, 2180 (1989).

C. R Poole, Jr., H. A. Farach, and R. J. Creswick,

Superconductivity,

Academic Press, New York, 1995.

Chapter 4

Models and Theories

Charles R Poole, Jr.

Department of Physics and Institute of Superconductivity,

University of South Carolina, Columbia, South Carolina

A. Introduction 53

B. London Equations 54

C. Ginzburg-Landau Theory 55

D. Bardeen-Cooper-Schrieffer Theory 58

E. Mechanisms for Cooper Pairing 60

E Critical State Models 61

G. Bean Model 62

H. Reversed Critical States and Hysteresis 64

I. Hubbard Models and Band Structure 66

References 69

Introduction

Superconductivity was discovered in 1911 by H. Kamerlingh Onnes when he

found that the element mercury went resistanceless below the critical temperature

T c = 4.1 K, and 25 years were to pass before Meissner and Ochsenfeld (1933)

found that superconductors also exclude magnetic flux. Two years later in 1935

the London brothers proposed a simple theory to explain the Meissner effect. In

1950 Ginzburg and Landau advanced a macroscopic theory that described

superconductivity in terms of an order parameter, and they provided a derivation

ISBN: 0-12-561460-8 HANDBOOK OF SUPERCONDUCTIVITY

All fights of reproduction in any form reserved.

54 Chapter 4: Models and Theories

of the London equations. That same year Frrhlich (1950) predicted the isotope

effect whereby the transition temperature of a superconducting element decreases

when its isotopic mass increases, a prediction confirmed forthwith by Maxwell

(1950) and also by Reynolds

et al.

(1950). In 1957 Bardeen, Cooper, and

Schrieffer proposed a microscopic theory that provides our present theoretical

understanding of the nature of superconductivity. They showed that bound

electron pairs called Cooper pairs carry the supercurrent, and that there is an

energy gap between the normal and superconducting states. The validity of the

earlier Ginzburg-Landau theory was not accepted worldwide until Gor'kov

showed in 1959 that it is derivable from the BCS theory.

The London equations provided an early simple model for describing

experimental results. The Bean model put forward in 1962 lacks theoretical

underpinning, but it has been surprisingly successful in describing some magnetic

properties of superconductors. There has been a great deal of recent interest in

the Hubbard and related models as ways of explaining the essential features of

superconductivity from a minimum of assumptions. The present chapter presents

some of the results of these models, as well as the results of the more

sophisticated theories mentioned earlier. No explanations or justifications of

the models and theories will be given, since many books are available to provide

this information.

London Equations

The 1935 theory of the London brothers provides the first and second London

equations, which relate the electric and magnetic fields E and B, respectively,

inside a superconductor to the current density J:

E --/~o22~J (1)

B- • J. (2)

The constant of proportionality in these expressions is the London penetration

depth 2L,

2 L --

(m/#onse2) 1/2,

(3)

where n s is the density of superconducting electrons. These expressions fumish

us with the modified Helmholtz equations

V2B- B/~[ (4)

v J- (s)

which are also satisfied by the vector potential A.

C. Ginzburg-Landau Theory 55

Ginzburg-Landau Theory

The Ginzburg-Landau (GL, 1950) phenomenological theory provides a good

description of many of the properties of both classical and high-temperature

superconductors. This theory assumes that in the superconducting state the

current is carried by super electrons of mass m*, charge e*, and density n*,

where we now know that m* - 2m*, e* - 2e, and n~ - 89 n s in terms of the free

electron values m, e, and n s, respectively. The order parameter ~b(r) is complex,

~b(r)- 14~(r)le i~ (6)

and its

square

j~)j2 is identified with the super electron density,

n~ -- J~bj2. (7)

The parameter ~b is zero above T c and increases continuously as the temperature is

decreased below To, as shown in Fig. 4.1a. Figure 4.1b shows the dependence

4~(x) on the distance x inside the surface of a superconductor.

Below, but close to, T c the Gibbs free energy per unit volume G s is

expanded in terms of the order parameter and then minimized with respect to

4) to provide the first GL equation in the London-Landau gauge (V. A = 0):

(1/2m*)[h2V2~ -

2ihe*A.

Vq5 - e*2A2~b] - a4~ - bl4~J2qb - 0. (8)

Minimization of G s with respect to the vector potential A provides the second GL

equation:

ihe*

e .2

V x (V x A) + 2m---2 (qS*Vqb - qbVqS*) +~-A[~bJ

2 -- 0.

(9)

These two coupled equations determine the properties of the superconducting

state.

It is assumed that below but near T c the parameter a depends linearly on the

temperature,

a(T) ~ ao[(T/Tc)-

1],

(10)

and b is independent of the temperature, where ao and b - b o are both positive so

a(T)

is negative below T c. Deep inside a superconductor in the absence of a

magnetic field, we have the following expression near T c

J~bJ 2 - n s* -

-a/b - (ao/bo)[1 - (T/Tc) ],

(11)

and the overall temperature dependence plotted in Fig. 4.1a. The coherence

length ~, the characteristic length over which 4) varies in the manner illustrated in

Fig. 4.1b, is the first of the two fundamental length scales from the GL theory:

~2 __

h2/2m, lal.

(12)