Potter T.D., Colman B.R. (co-chief editors). The handbook of weather, climate, and water: dynamics, climate physical meteorology, weather systems, and measurements

Подождите немного. Документ загружается.

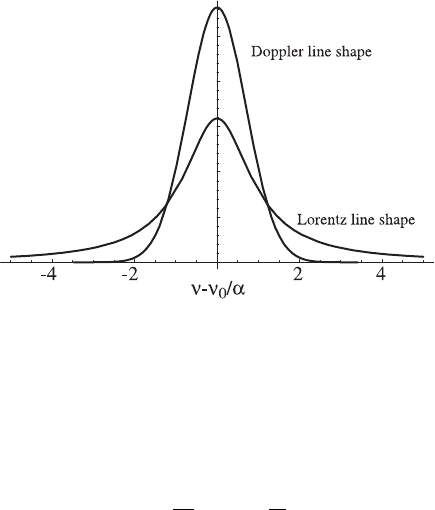
examine the relative importance of Doppler and pressure broadening before invok-

ing anything more complicated. A useful approximation is

 10

12

ð27Þ

when n

is measured in hertz and p in millibars. Throughout most of the spectrum

and most of the atmosphere this ratio is much less than one, telling us that the

Lorentz line proﬁle is usually a pretty good description of line shape.

Practical Applications

Absorption spectra almost never need to be determined directly from spectroscopy.

Spectroscopic databases (HITRAN is pop ular) have been compiled for all the gases

in Earth’s atmosphere. These databases contain the line centers and parameters

describing line shape as a function of temperature and pressure, and can be accessed

with standard programs (e.g., LBLRTM) that provide the amount of absorption at

very high spectral resolution.

Radiative Transfer Equation for Absorption

We are at last ready to compute the fate of radiation as it travels through a medi um.

Radiation may be absorbed or emitted by the medium, and may also be scattered or

redirected without a change in intensity. We will develop the radiative transfer

equation by adding each process in turn in order to keep the mathematics clear.

We will begin by considering a medium that absorbs but does not emit or scatter

radiation. This is the framework we might use, for example, to describe the absorp-

Figure 5 Lorentz and Doppler line shapes for equivalent line strengths and widths. Line

wings are more strongly affected by pressure than Doppler broadening.

316

RADIATION IN THE ATMOSPHERE: FOUNDATIONS

tion of ultraviolet or visible light by gases in the atmosphere, where relatively low

temperatures mean that emission is effectively zero.

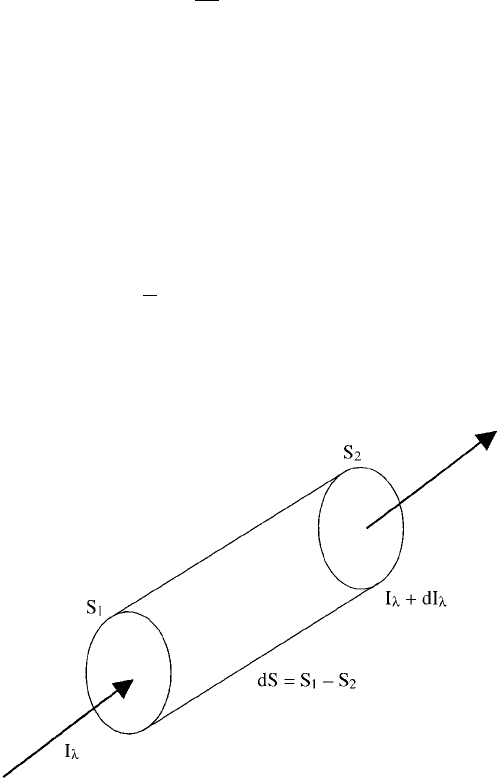
Imagine a pencil of monochromatic radiation crossing a small distance ds

between two points S

and S

, as illustrated in Figure 6. The amount of radiation

absorbed along this path depends linearly on the amount of incident radiation (more

incoming photons means a greater likelihood that a photon will strike a molecule),

the gas density (higher density increases the number of molecules encountered), and

on how effectively the molecules absorb radiation at this wavelength. These are the

three factors that appear in the radiative transfer equation for absorption:

¼I

r ð28Þ

where r is the density of the absorbing gas and k

the mass absorption coefﬁcient

=kg). Notice that k

has the same units as absorption line strength S. In fact, the

absorption coefﬁcient at some wavelength due to one particular line i is the product

of the line shape and the line strength:

ðnÞ¼S

f ðn  n

Þð29Þ

and k

is the sum contributions from all lines from all gases.

The radiative transfer equation can be integrated along the path between S

and S

¼ ln I



¼

r ds ð30Þ

ðS

Þ¼I

ðS

Þexp 

r ds

ð31Þ

Figure 6 Beam of radiation passing through an absorbing medium.

4 ABSORPTION AND EMISSION IN GASES: SPECTROSCOPY 317

where we leave the integral over the path unevaluated because r and k

may change

with distance. We insist that the light be monochromatic since the integration does

not make sense if k

is variable. Equation (31) is called Beer’s law, or more formally

the Beer–Lamber t–Bouguer law.

How can we relate a path between arbitrary points S

and S

to the atmosphere?

Two assumptions are usually made: that the atmosphere is much more variable in the

vertical than in the horizontal, and that Earth is so large that the surface can be

considered ﬂat. These simpliﬁcations lead to the plane-parallel coordinate system, in

which directions are speciﬁed throu gh zenith angle y and azimuthal angle j but the

medium varies only with vertical position z. In this system the path between S

and

is related to the vertical displacement by 1=m, so we may write

ðz

Þ¼I

ðz

Þexp 

r dz

ð32Þ

The integral in the exponential deﬁnes the optical thickness t, also called the optical

depth:

t ¼

r dz ð33Þ

The minus sign in (33) is an unfortunate hangover from the days when radiative

transfer was dominated by astrophysicists. Since they were thinking about other

stars, they set up a coordinate system in which t ¼0 at the top of the atmosphere,

so that m dt < 0. Though it is a little confusing, (33) does lead to much simpler forms

of both the radiative transfer equation

¼ I

ð34Þ

and to a more transparent form of Beer’s law

ðt

Þ¼I

ðt

Þexp

ðt

 t



¼ I

ðt

Þexp

ðt

 t

jmj



ð35Þ

For downwelling radiation t

> t

and m < 0 and for upwelling radiation both

signs are reversed, so intensity always decreases along the path. According to

Beer’s law, then, intensity in an absorbing medium falls off exponentially with

optical depth.

The transmissivity T

of the layer between z

and z

is deﬁned as

ðz

ð36Þ

318 RADIATION IN THE ATMOSPHERE: FOUNDATIONS

which for an absorbing medium T

can be computed as

¼ exp

jt

 t

jmj



ð37Þ

In a strictly absorbing medium the light that is not transmitted must be absorbed; so

the absorptivity a

of the medium is

¼ 1  T

¼ 1  exp

 t

jmj



ð38Þ

Computing Optical Depth along Inhomogeneous Paths

Optical depth is formally deﬁned by (33), but computing its value is not always

straightforward since both density and the absorption coefﬁcient may change with

height in the atmosphere. We can roughly account for the change in density with

height by deﬁning the speciﬁc gas ratio q ¼r=r

air

and invoking the hydrostatic

equation dp=dz ¼rg in the deﬁnition of optical mass u:

uðp

; p

Þ¼

qdp ð39Þ

which has dimensions of mass per unit area.

The value of k

may also change with height if, for example, the wavelength in

question is on the wing of an absorption line, so that the local strength changes as

pressure and temperature change. We could adjust k

to some average value along

the path. It is more common, however, to scale the optical mass to the reference

temperature T

and pressure p

at which the mass absorption coefﬁcient is

measured. There are various approaches to scaling, though a common tactic is

to compute a scaled absorber amount

uu as

uu ¼ u



ð40Þ

where m and n depend on the gas, and p

and T

are the effective pressure and

temperature along the path, computed for temperature a s

Tdu

ð41Þ

and similarly for pressure.

4 ABSORPTION AND EMISSION IN GASES: SPECTROSCOPY 319

Radiative Transfer Equation for Emission and Absorption

Imagine next a material that emits and absorb s at a wavelength l . This might apply,

for example, to the transfer of infrared radia tion through Earth’s atmosphere: Vibra-

tional transitions in common gases give rise to absorption lines in the infrared, where

temperatures through most of the atmosphere give rise to strong emission.

Kirchoff’s law tells us that the emission and absorption per amount of material (or

per unit of optical depth) must be the same, but emission adds to the intensity while

absorption reduces it. Since m dt < 0, the radiative transfer equation is

¼ I

 B

ð42Þ

This relation, known as Schwartzchild’s equation, holds strictly for any medium that

does not scatter radiation at the wavelength in question; (34) is a useful approxi-

mation when temperatures are such that B

is very small at the wavelength in

question.

We can solve (42) using an integrating factor: We multiply both sides of the

equation by e

t=m

=m and collect terms in I

t=m

 e

t=m

¼e

t=m

ð43Þ

t=m

¼B

t=m

ð44Þ

To ﬁnd the intensity propagating in direction m at some vertical optical depth t,we

integrate (44) starting at one boundary, being careful to account for the sign of m

and for the fact that B

may vary with height. The downwelling intensity I

,at

optical depth t, for example, is

ðtÞe

t=m

 I

ð0Þ¼

1

ðt

Þe

t

ð45Þ

ðtÞ¼I

ð0Þe

t=m



ðt

Þe

ðtt

Þ=m

ð46Þ

while the upwelling intensity is

ðtÞ¼I

ðt



Þe

ðt



tÞ=m



ðt

Þe

ðt

t



Þ=m

ð47Þ

where t* refers to the bottom of the atmosphere.

320 RADIATION IN THE ATMOSPHERE: FOUNDATIONS

Equations (46) and (47) tell us that the downwelling intensity at some height t

consists of the intensit y incident at the boundary and attenuated by the intervening

medium (the ﬁrst term on the right-hand side) plus contributions from every other part

of the medium (the integral over the blackbody contribution at every height), each

attenuated by the medium between the source at t

and the observation location t.

As an example, imagine a satellite in orbit at the top of the atmosphere, looking

straight down at the ground, which has emissivity 1 and is at temperature 294 K. At

10 mm, blackbody emission from the ground is found with (10) and (11) as

(294 K) ¼2.85 W=m

2

str mm. The clear sky is nearly transparent (t 0) at

10 mm, so the upwelling nadir-directed (m ¼1) intensity at the top of the atmosphere

is essentially the same as the intensity at the ground. But if a thin (t ¼1at10mm),

cold (T ¼195 K) cirr us cloud drifts below the satellite, the outgoing intensity will

be reduced. If we assume that the cloud has constant temperature, we can ﬁnd the

upwelling intensity with (47), using t ¼0 at the top of the cloud, t* ¼1 at the cloud

base, and B

) ¼B

(195 K) for 0 < t

< t*:

ðtÞ¼B

ð294 KÞe

1

þ B

ð195 KÞð1  e

1

Þ¼1:2W=m

2

str mm ð48Þ

which corresponds to a brightness temperature of T

¼250 K. This effect is clear in

infrared satellite imagery: Thick cirrus clouds appear much colder (i.e., have lower

brightness temperatures) than thin ones at the same level.

It seems on the face of things that computing radiative transfer in the infrared is

not that hard, since we can now predict the intensity and ﬂux using (46) and (47) if

we know the boundary conditions and the state of the atmosphere. Life, alas, is not

that simple. Any practical use of radiative transfer involves integration over some

spectral inter val, and spectral integrati on in the infrared is where things bec ome

difﬁcult. We learned in the section on spectroscopy that the absorption and emission

characteristics of gases change very rapidly with wavelength, being large near

absorption lines and small elsewhere. The atmosphere is composed of many

gases, so the absorption structure as a function of wavelength is extremely rich.

Brute force spectral integration, while theoretically possible, is computationally

prohibitive in practice. We will address more practical methods for spectral integra-

tion, including band models and k distrib utions, in the next chapter.

5 FULL RADIATIVE TRANSFER EQUATION, INCLUDING

ABSORPTION, EMISSION, AND SCATTERING

What is Scattering?

The absorption of radiation by a gas molecule is a two-step process. First, the photon

must pass close enou gh to the molecule for an interaction to occur, and second, the

photon’s energy must match the difference between the molecule’s current state and

another allowed state. But what happens to those photons that inte ract with mole-

5 FULL RADIATIVE TRANSFER EQUATION 321

cules but whose energies do not match an allowed transition? The se photons essen-

tially bounce off the molecule and are redirected; we call this process scattering.

Gases do scatter radiation, but the vast majority of scattering in the atmosphere

occurs when light interacts with condensed materials, primarily clouds and aerosols.

Formally, we say that photons that are absorbed undergo inelastic interactions with

the medium, while elastic collisions cause scattering. The likelihood of each kind of

interaction need not be the same; that is, the extinction coefﬁcients for scattering and

absorption are not ident ical.

The radiative transfer equation as we have been writing it describes intensity, a

quantity associated with a particular direction of propagation. When we discuss

scattering, the direction of the beam becomes more important than when considering

only absorption and emission because photons can be scattered both out of the beam

into other directions and into the beam from radiation traveling in any other

direction.

Accounting for Scattering

When we ﬁrst wrote the radiative transfer equation, we assumed that the medium

absorbed but did not emit radiation at the wavelength in question, as occurs during

the absorption of solar radiation in Earth’s atmosphere. In going from (34) to (42) we

included the effects of emission, as when considering the transfer of infra red radia-

tion in the atmosphere. The blackbody emission contribution in (42) is called a

source term. Scattering from the beam into other directions is an additional reduction

in intensity, while scattering into the beam from other directions adds a second

source term.

To write the complete radiative transfer equation, we must distinguish the amount

of absorption and emission along the path from the amount of scatteri ng. We do so

by introducing a mass scattering coefﬁcient k

with dimensions of area per mass, as

an analog to the mass absorption coefﬁcient k

. Both absorption and scattering

diminish the beam, while scattering of radiation traveling in any other direc tion

into the beam can add to the intensity. The full radiative transfer equation is therefore

ðm; jÞ

¼ðk

þ k

ÞrI

ðm; jÞþk

1

Pðm

; j

! m; jÞIðm

; j

Þdm

ð49Þ

where we have made explicit the direc tion of the beam (speciﬁed by m, j). The last

term in (49) accounts for the scattering of radiation into the beam traveling in

direction m,j from every other direction. The quantity P(m

!m,j) is called

the single scattering phase function, or often simply the phase function, and

describes how likely it is that radiation traveling in the m

direction will be

scattered into the m,j direction. The phase function is reciprocal, so that

322 RADIATION IN THE ATMOSPHERE: FOUNDATIONS

P(m

!m,j) ¼P(m,j !m

), and is deﬁned such that the integral over the

entire sphere is 4p.

We divide both sides of the equation by (k

þ k

)r and relate path length

differential to the vertical displacement to obtain

ðm;jÞ

¼ I

ðm;jÞð1  o

ÞB



1

Pðm

! m;jÞIðm

Þdm

ð50Þ

where we have now deﬁned the single scattering albedo o

¼k

=(k

þ k

), which

is the likelihood that a photon is scattered rather than absorbed at each interaction.

Single scattering albedo varies between zero and one; the lower limit corresponds to

complete absorption and the upper to complete scattering.

Equation (50) is the plane parallel, unpolarized, monochromatic radiative transfer

equation in full detail. Despite its length, it describes only four processes: extinction

by absorption and by scattering out of the beam into other directions, emission into

the beam, and scattering into the beam from every other direction. The equation is,

unfortunately, quite difﬁcult to solve because it is an integrodifferential equation for

intensity; that is, intensity appears both in the differential on the left-hand side and as

part of the integral on the right-hand side of the equation.

Before we can even begin to solve this equation, we have to come to grips with

the way particles scatter light. When we consider absorption and emission, we need

only to determine the mass absorption coefﬁcient k

. When we include scattering

in the radiative transfer equation, though, we require three additional pieces of

information: the mass scattering coefﬁcient k

, along with the phase function

P(m

!m,j) and single scattering albedo o

6 SINGLE SCATTERING

When we are concerned with emission and absorption, it is spectroscopy, a com-

bination of quantum mecha nics and statistical mechanics, that lets us determine k

from knowledge of the temperature, pressure, and chemical composition of the

atmosphere. To compute the single scattering parameters within a volume, we

begin with knowledge of the way light interacts with individual particles, which

comes from solutions to Maxwell’s equations; this knowledge is then combined with

information about the statistics of different particle types within the volume.

Scattering from a particle is most naturally computed in a frame of reference

centered on the particle. In particular, it is easiest to describe the phase function in

terms of a scattering angle Y between the incident and scattered radiation. The

phase function is often summarized using the asymmetry parameter g:

g ¼

1

cos YPðYÞd cos Y ð51Þ

6 SINGLE SCATTERING 323

which is the average cosine of the scatteri ng angle. When g > 0, more light is

scattered into the forward than backward direction. Pðm

! m;jÞ is, of course,

related to P(Y):

cos Y ¼ m

m þ

ﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃ

ð1  m

p ﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃ

ð1  m

cosðj

 jÞð52Þ

Computing Scattering from a Single Particle

The task of computing the intensity scattered from a single particle is conceptually

straightforward: Maxwell’s equations are solved inside and outside the particle

subject to the boundary conditions on the particle’s surface. In practice this is

such a difﬁcult feat that it is possible only in circumstances when geometric or

size considerations are favorable, or when it is possible to make simplifying assump-

tions of one kind or another.

In the electromagnetic ter ms of Maxwell’s equations, cloud drops and aerosol

drops differ from the gaseous atmosphere only in their index of refraction

m ¼n

þ in

. The index of refraction is complex: The real part primarily determines

the speed of light within the medium, while the imaginary part determines the

amount of absorption per amount of material. The value of m varies with wavelength

and can also depend on the state of the material; the indices of refraction of water

and ice, for example, can differ dramatically at certain wavelengths, as Figure 7

shows.

Imagine a particle with monochromatic radiation I

inc

incident upon it. The total

surface area projected in the direction of the beam’s origin is called the particle’s

geometric cross section C

geo

, and the power incident on the particle is P

inc

¼C

geo

inc

We can generalize this idea to deﬁne scattering and absorption cross sections for the

particle though the rate at which each process removes energy from the beam:

sca

¼P

sca

inc

, C

abs

¼P

abs

inc

. Extinction includes both scattering and absorption,

so the extinction cross section C

ext

is the sum of C

sca

and C

ext

. The radiative cross

sections of a particle are related to its geometric cross section but also depend on the

particle shape and index of refraction. This makes it useful to unscramble the two

inﬂuences, deﬁning efﬁciencies Q

¼C

geo

, where j denotes one of scattering,

absorption, or extinction.

The single scattering parameters of a particle depend on the particle’s size,

composition, and shape, and on the wavelength of radiation being scattered through

the index of refraction. The relative sizes of the particle and the radiation determine

the methods that must be used to compute single scatteri ng parameters. The relation-

ship is embodied in the size parameter x, the ratio between some characteristic radius

r and the wavelength; for spheres, for example, the size parameter is deﬁned as

x ¼2pr= l.

324 RADIATION IN THE ATMOSPHERE: FOUNDATIONS

Figure 7 Indices of refraction for liquid water and ice as a function of wavelength. Upper set of panels is a closer

look at the left-hand portion of the lower set of panels. See ftp site for color image.

325