Pugnaire F.I. Valladares F. Functional Plant Ecology

Подождите немного. Документ загружается.

the shoot outside the chamber. When E ¼0andC

soil

> 0 we could expect gutation (exudation

of water from leaves); this forward direction of current flow is permitted by the rectifier.

When E > 0 and C

soil

is positive enough, gutation can occur simultaneously with evaporation

when C

leaf

> 0; the rectifier permits this additional current flow (see also Wei et al. 1999).

An alternative representation of evaporation from leaves would be achieved by including

an additional conductance element for the vapor phase conductance, K

vapor

(analogous to

ﬃ g

), with an additional water potential drop from the leaf to the ambient air outside the

Gymnosperms

Angiosperms

Tropical Ang. trees

Tropical shrubs

Tropical lianas

Hemiepiphytes

wood per m

leaves)

(kg s

−1

MPa

−1

)

(kg s

−1

MPa

−1

)

−6

−5

−4

−3

−2

Temperate Ang. trees

−5

0.1 1 10 100

−4

−3

−2

FIGURE 6.8 Ranges of hydraulic parameters by phylogeny or growth form. Horizontal bars demark the

ranges read from the bottom axis of each parameter, where H

is the Huber value, K

is the leaf-specific

conductivity, and K

is the specific conductivity. Values represent ranges for 48 species. (Adapted from

Patin

o, S., Tyree, M.T., and Herre, E.A., New Phytol., 129, 125, 1995. With permission.)

Francisco Pugnaire/Functional Plant Ecology 7488_C006 Final Proof page 190 10.5.2007 2:47pm Compositor Name: VBalamugundan

190 Functional Plant Ecology

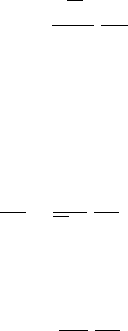
leaf (C

air

). K

vapor

would be orders of magnitude smaller than the whole-plant conductance

liquid

), and hence would dominate and control E and hence behave like a constant current

source. There are two disadvantages to using this representation. First, g

is never measured

in the same units as K

liquid

, making it difficult to compare values with those in the literature.

Second, g

measured in the units of K

liquid

would no longer be a constant, that is, its value in

theory would change with C in the vapor phase. This can be seen immediately by looking at

Equation 6.2 and Equation 6.4, from which we can get

vapor

, (6:14)

where C is the concentration of water. In the liquid phase, C is nearly a constant, but in the

vapor phase, the concentration of water vapor can easily change by a factor of 10 from the

evaporating surface in a leaf to the bulk air. The value of g

in Equation 6.8 is superior in that

it depends only on the geometry of the stomatal pores; this follows because in the vapor phase

(6:15)

hence,

vapor

, (6:16)

which is Fick’s law for water vapor transport in air. The coefficient RT=f is independent of

dC=dx. Equation 6.8 can be viewed as derived from Fick’s law with account taken of the

specific geometry of water diffusion through stomates and replacing dC=dx with the gradient

in mole fraction of water vapor.

PARAMETERS AND CONCEPTS TO DESCRIBE HYDRAULIC ARCHITECTURE

The hydraulic architecture of a plant can be defined as a quantitative description of the plant in

terms of the Ohm’s law analog using a simple linear model of conductance elements or a complex

branched catena of a few or even thousands of conductance elements (Figure 6.7). The conduc-

tance elements are quantified by measurements made on excised stem segments for branched

catena models and by measurements on whole roots and shoots for simple linear models.

Measurements on stem segments are performed with a conductivity apparatus. Excised

stem segments are fitted into water-filled lengths of plastic tubing. One end of the segment of

length (L, m) is connected via tubing to an upper reservoir of water and the other end to a

lower reservoir. The height difference between the reservoirs is usually set at 0.3–1 m to create

a pressure drop DP of 3–10 kPa across the stem segment. The lower reservoir is usually placed

on top of a digital balance to measure water flow rate, F,inkgs

1

. The fundamental

parameter measured is the hydraulic conductivity (K

), defined as

¼ F=(DP=L): (6:17)

Values of K

are usually measured for stems of different diameter, D, and regressions are used

to obtain allometric relationships of K

versus diameter of the form

¼ AD

, (6:18)

where A and B are regression constants.

Francisco Pugnaire/Functional Plant Ecology 7488_C006 Final Proof page 191 10.5.2007 2:47pm Compositor Name: VBalamugundan

Water Relations and Hydraulic Architecture 191

Stem segments can be viewed as bundles of conduits (vessels or tracheids) with a certain

diameter and number of conduits per unit cross section. If all of the conduits were of the same

diameter and number per unit cross section, then B ¼2, because K

would increase with

number of conduits in parallel, which would increase with cross section, which is proportional

to diameter squared. Usually, B is found to be more than 2 but less than 3 because the

diameter of conduits tends to increase with stem diameter in most plants. According to the

Hagen–Poiseuille law, the K

of a single conduit of diameter, d, increases in proportion to d

;

therefore, the conductance of a stem segment with N conduits would be proportional to Nd

Although you cannot pack as many big-diameter conduits into a stem segment as small-

diameter conduits, there is a net gain in K

for a stem segment to have bigger diameter conduits,

although fewer would fit into that available space. To prove this, let us imagine a stem segment

of 1 mm diameter with 1000 conduits of d

¼0.01 mm diameter each and another stem

segment of 1 mm diameter with 250 conduits of d

¼0.02 mm diameter each. The cross-

sectional area of each conduit is pd

=4. Both segments would have the same cross-sectional

area of conduits since 1000 pd

2=4

¼ 250 pd

=4, but each conduit in the latter would be 16 times

more conductive than the former because d

¼ 16 d

; therefore, although there are only one-

fourth as many conduits of diameter d

and d

, the stem is four times more conductive.

Since K

of stem segments depends on stem cross section, one useful way of scaling K

to divide it by stem cross section to yield specific conductivity, K

. Specific conductivity is a

measure of the efficiency of stems to conduct water. The efficiency of stems increases with the

number of conduits per unit cross section and with their diameter to the fourth power. In

large woody stems, the central core is often nonconductive heartwood. It is often better to

calculate K

from K

, where A

is the cross-sectional area of conductive sapwood.

Leaf-specific conductivity (K

), also known as LSC (Tyree and Ewers 1991), is equal to K

divided by the leaf area distal to the segment (A

). This is a measure of the hydraulic

sufficiency of the segment to supply water to leaves distal to that segment. If we know the

mean evaporative flux density (E,kgs

1

2

) from the leaves supplied by the stem segment

and we ignore water storage capacitance, then the pressure gradient through the segment

(dP=dx) ¼E=K

. Therefore, the higher the K

is, the lower the dP=dx required to allow for a

particular transpiration rate.

In simple linear Ohm’s law models, whole-shoot and whole-root conductances (k

and k

respectively) are measured using a high-pressure flowmeter (HPFM; see later). These con-

ductances are usually defined as the ratio of flow, F, across the whole root or shoot divided by

the pressure drop, DP; hence, it differs from K

, K

, and K

in that root or shoot length is not

taken into account. The word conductivity is usually used when L is taken into account in the

calculation, and conductance is used when L is not used in the calculation. Because a large

plant or root becomes more conductive than small plants, some suitable means of normal-

ization for plant size is needed. One way to do this is to calculate leaf-specific conductances,

that is, K

¼K

and K

¼k

. The advantage of this versus other kinds of scaling is

discussed in Section ‘‘Root, Shoot, and Leaf Hydraulic Conductances’’.

The Huber value (H

) is defined as the sapwood cross-section (or sometimes the stem

cross-section) divided by the leaf area distal to the segment. Because, the H

is in units of m

stem area per m

leaf area, if is often written without dimension. It is a measurement of the

investment of stem tissue per unit leaf area fed. It follows from the definitions mentioned

earlier that K

¼H

Figure 6.8 summarizes the known ranges of hydraulic architecture parameters in

48 taxa covering a range of growth forms and phylogenies. Comparisons of mean values

between species are difficult because K

, K

, and H

often change significantly with stem

diameter, D. For example, K

, and K

can be 10–100 times greater when measured in the bole

of trees (D ¼300 mm) than when measured in young branches (D ¼3 mm). Sometimes,

differences between species in K

or K

measured at D ¼6 mm may be reversed at D ¼60 mm;

Francisco Pugnaire/Functional Plant Ecology 7488_C006 Final Proof page 192 10.5.2007 2:47pm Compositor Name: VBalamugundan

192 Functional Plant Ecology

furthermore, stem morphologies may be such that the smallest segments bearing leaves were

20 mm in diameter in some species but just 3 mm in another. The mean values in Figure 6.8

were computed from regression values at D ¼15 mm, except for three tropical species with

large stems for which we used D ¼45 mm because smaller branches did not exist.

PATTERNS OF HYDRAULIC ARCHITECTURE OF SHOOTS

Values of K

have been applied to complex ‘‘hydraulic maps’’ in which the aboveground

portion of trees, were represented by hundreds to thousands of conductance elements (Figure

6.7). Using known values of K

and E, it is possible to calculate P

versus path length from

the base of a tree to selected branch tips (Figure 6.9). Some species are so conductive (large K

values) that the predicted drop in P

is little more than needed to lift water against gravity (see

Schefflera in Figure 6.9). In other species, gradients in P

become very steep near branch tips

(see Thuja in Figure 6.9). The predicted gradients of P

become steeper in small branches of

trees because K

is often lower in small-diameter branches than in big-diameter branches. In

20 species of angiosperms, the value of K

was found to be proportional to stem diameter, D,

to the power of 0.5–2.0 depending on the species (Tyree and Ewers 1991, Patin

o et al. 1995,

Zotz et al. 1998). The increase in K

with diameter could be due to an increase in H

or K

since K

¼H

, but in most cases, H

was found to be approximately constant with D so the

change was due to an increase in K

with D. The exceptions seem to be gymnosperms with

strong apical dominance, where H

increases toward the apex, that is, decreases with increas-

ing D (Ewers and Zimmermann 1984a,b). In one angiosperm, Ficus dugandii, H

was found to

increase with D to the power of 1.0 (Patin

o et al. 1995).

−2.0

−1.8

−1.6

−1.4

−1.2

−1.0

−0.8

−0.6

−0.4

−0.2

24681012

Path len

th (m)

Schefflera E = 6 ⫻ 10

−5

Acer E = 4 ⫻ 10

−5

Thuja E = 2 ⫻ 10

−5

Stem P

(MPa)

14 16 18 20 22

FIGURE 6.9 Pressure profiles in three large trees, that is, computed change in xylem pressure (P

) versus

path length. P

values were computed from the base of each tree to a few randomly selected branch tips.

The drooping nature of these plots near the apices of the branches is caused by the decline of leaf-specific

conductivity (K

) from base to apex of the trees. The pressure profiles do not include pressure drops

across roots or leaves. In some species, pressure drop across leaves can be more than shown. The

pressure drop across roots is generally equal to that across the shoots (including leaves). E, evaporative

flux density in kg s

1

2

Francisco Pugnaire/Functional Plant Ecology 7488_C006 Final Proof page 193 10.5.2007 2:47pm Compositor Name: VBalamugundan

Water Relations and Hydraulic Architecture 193

There appear to be no hydraulic constrictions at branch junctions in woody plants (Tyree

and Alexander 1993), that is, the hydraulic conductance of water passing through branch

junctions is approximately the same as in equal lengths of stem segments above- and below-

branch junctions. This is contrary to earlier reports of major constrictions in branch junc-

tions, but the number of measurements in these reports were too few to draw statistically

provable conclusions (Ewers and Zimmermann 1984a,b, Zimmermann 1978). Unfortunately,

a myth has arisen regarding the hydraulics of branch junctions because these earlier, prelimi-

nary studies have been frequently cited.

ROOT,SHOOT, AND LEAF HYDRAULIC CONDUCTANCES

Most studies have focused on the hydraulic architecture of large woody tropical plants, for

example, trees, shrubs, and vines (Ewers et al. 199, Patin

o et al. 1995, Tyree and Ewers 1996).

Parameters measured generally have been confined to hydraulic conductance of woody

shoots. However, relatively little is known about total root conductance of plants relative

to shoot conductances, and little is known about the conductivity of leaves relative to shoots.

In large woody plants, the shoots of rapidly growing trees appear to be more conductive than

slowly growing trees.

The recent development of an HPFM (Yang and Tyree 1994, Tyree et al. 1995) allows the

rapid measurement of root and shoot hydraulic conductance of seedlings to saplings with

stem diameters from 1 to 50 mm. Thus, it is now possible to study the growth dynamics of

seedlings while monitoring dynamic changes in hydraulic conductance of roots and shoots.

This ability raises the question of how best to scale conductance parameters to reveal

ecological adaptation to light regimes. Because more thought has gone into scaling of shoot

parameters (Tyree and Ewers 1996) than root parameters, a review of arguments for roots

seems appropriate.

Root conductance (k

) can be defined as water flow rate (kg s

1

) per unit pressure drop

(MPa) driving flow through the entire root system. Values of k

could be scaled by dividing by

some measure of root size (root surface area, total root length, or mass) or by dividing k

leaf surface area. Division by root surface area (A

) is justified by an analysis of axial versus

radial resistances to water flow in roots. In the radial pathway, water flows from the root

surface to the xylem vessels through nonvascular tissue. In the axial pathway, water flow is

predominately through vessels. The resistance of the radial path is usually more than the axial

path (French and Steudle 1989, North et al. 1992). Most water uptake is presumed to occur in

fine roots (<2 mm diameter) and fine root surface area is usually greater than 90% of the total

root surface area (M.T. Tyree, personal observation). Root uptake of water would appear to

be limited by root surface area, and hence it is reasonable to divide k

by A

, yielding a

measure of root efficiency. Some roots are more efficient than others. Division of k

by total

root length (L) is not as desirable, but is justified because A

and L are correlated approxi-

mately and L can be estimated by a low-cost, line-intersection technique rather than a

high-cost, image-analysis technique.

Scaling by root mass is justified by consideration of the cost of resource allocation.

Plants must invest a lot of carbon into roots to grow and maintain them. The benefit derived

from this carbon investment is enhanced scavenging for water and mineral nutrient resource.

Total root dry weight (TRDW) is a measure of carbon investment into roots. Thus, the

carbon efficiency of roots might be measured in terms of K

=TRDW, A

=TRDW, or

L=TRDW. Scaling by TRDW provides information of ecological rather than physiological

importance.

Scaling of k

by leaf surface area (A

) provides an estimate of the sufficiency of the roots

to provide water to leaves. The physiological justification of scaling k

to the leaf surface area

) comes from an analysis of the Ohm’s law analog for water flow from soil to leaf (van den

Francisco Pugnaire/Functional Plant Ecology 7488_C006 Final Proof page 194 10.5.2007 2:47pm Compositor Name: VBalamugundan

194 Functional Plant Ecology

Honert 1948). The Ohm’s law analog describes water flow rate (F,kgs

1

) in terms of the

difference in water potential between the soil (C

soil

) and the leaf (C

)

soil

C

¼ (1=k

soil

þ 1=k

)F, (6:19a)

where k

soil

is the hydraulic conductance of the soil. Because it is usually assumed that k

soil



and k

except in dry soils, 1=k

soil

can be ignored. Leaf water potential is approximated by

ﬃ C

soil

(1=k

þ 1=k

)F: (6:19b)

Or, if we wish to express Equation 6.19b in terms of leaf area and average evaporative flux

density (E ), we have

ﬃ C

soil

(1=k

þ 1=k

F: (6:20)

This equation also can be rewritten so that root and shoot conductance are scaled to leaf

surface areas, i.e., to give leaf-specific shoot and root conductances, K

¼k

and

¼k

, respectively:

ﬃ C

soil

(1=k

þ 1=k

)E: (6:21)

Meristem growth and gas exchange are maximal when water stress is small, that is, when C

is near zero. From Equation 6.21 it can be seen that the advantage of high K

and K

is that

is closer to C

soil

. Because leaf-specific stem-segment conductivities K

are high in adult

pioneer trees, the water potential drop from soil to leaf is much smaller than in old-forest

species (Machado and Tyree 1994). This may promote rapid extension growth of meristems

in pioneers compared with old-forest species. In addition, stomatal conductance (g

)and

therefore net assimilation rate are reduced when C

is too low. During the first 60 days of

growth of Quercus rubra L. seedlings, there was a strong correlation between midday g

and

leaf-specific plant conductance, G ¼k

, where k

¼k

=(k

þk

) (Ren and Sucoff 1995).

This suggests that whole-seedling hydraulic conductance is limiting g

though its effect on C

There is also reason to believe that whole-shoot conductance limits g

in mature trees of Acer

saccharum Marsh (Yang Tyree 1993). Thus, high values of K

and K

may promote both

rapid extension growth and high net assimilation rates in pioneers. See Tyree 2003 for a recent

review of how whole-plant hydraulic conductance influences gas exchange and plant

performance.

Scaling is always necessary to normalize for plant size. As seedlings grow exponentially

in size, we would expect an approximately proportional increase in k

and k

. Since roots

and shoots both supply water to leaves and since an increase in leaf area means an increase

in rate of water loss per plant, we would expect k

and k

to be approximately proportional

to A

The major resistance (¼inverse conductance) to liquid water flow in plants resides in the

nonvascular pathways, that is, the radial pathway for water uptake in young roots and in

the cells between leaf veins and the evaporating surfaces of leaves. Nonvascular resistance

can be 60%–90% of the total plant resistance to water flow, although the total path

length may be less than 1 mm. Although water flows through distances of 1–100 m in the

vascular pathways from root vessel to stems to leaf vessels, the hydraulic resistance of

this pathway rarely dominates. The biggest resistance to water flow (liquid and vapor) from

the soil to the atmosphere resides in the vapor transport phase. The rate of flow from the leaf

to the atmosphere is determined primarily by the stomata, as discussed in Section ‘‘Water

Relations of Whole Plants.’’

Francisco Pugnaire/Functional Plant Ecology 7488_C006 Final Proof page 195 10.5.2007 2:47pm Compositor Name: VBalamugundan

Water Relations and Hydraulic Architecture 195

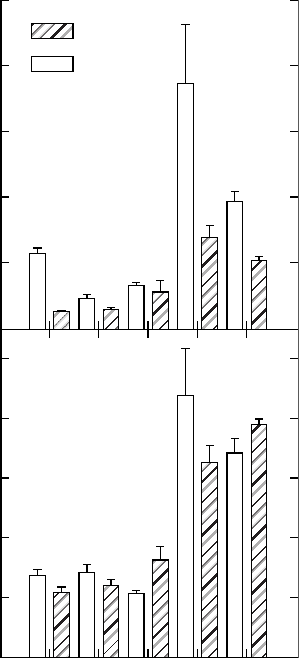
Early successional (pioneer) species grow more rapidly and require higher light levels to

survive than late successional (old-forest) species. A pattern is emerging that shows that the

dry matter cost of root and shoot conductance is less in pioneer versus old-forest species, and

the leaf-specific root and shoot conductances are higher. Hence, scaling hydraulic parameters

by leaf area is ecologically meaningful. In Figure 6.10 (top), the root and shoot conductances

are scaled by root and shoot dry weights, respectively. In Figure 6.10 (bottom), the root and

shoot conductance are scaled by dividing both by leaf area. In both cases, the adaptive

advantages of the pioneer species become evident. All pioneer species differed significantly

from the nonpioneer species, although all species were growing in the same light regime.

Figure 6.10 illustrates two advantages of pioneers versus other species in this study. The higher

values of K

and K

mean that the pioneer species can maintain less negative leaf water

Gs Pr

Species

K/A

(kg s

−1

MPa

−1

)

K/DW (kg s

−1

MPa

−1

)

Am Ma

Roots

Shoots

FIGURE 6.10 Hydraulic conductances of shoots and roots scaled to dry weight or leaf area (top) K

per

unit total root dry weight (TRDW) and K

per unit shoot dry weight. (Bottom) K

and K

, both scaled

to leaf are (A

). Error bars are SEM, n ¼23–36. Species are: Tt, Trichilia tuberculata; Gs, Gustavia

superba; Pr, Pouteria reticulata; Am, Apeiba membranacea; and Ma, Miconia argentea. Ma, Am, and Pr

are old-forest species, and Pr and Gs are pioneer species. Root and shoot means for Am and Ma were

significantly different from corresponding root and shoot means for Tt, Pr, and Gs in both (top) and

(bottom) (Tukey test, P  0.05). (From Tyree, M.T., Velez, V., Dalling, J.W., Oecologia, 114, 293–298,

1998. With permission.)

Francisco Pugnaire/Functional Plant Ecology 7488_C006 Final Proof page 196 10.5.2007 2:47pm Compositor Name: VBalamugundan

196 Functional Plant Ecology

potentials than the other species at any given transpiration rate. This might lead to higher rates

of extension growth and net assimilation. The higher values of K

=DW and K

=DW in

pioneers means that pioneers spend less carbon to provide efficient hydraulic pathways

than do the other species. Both of these advantages (Figure 6.10, top and bottom) mean

that pioneers can be more competitive in gap environments than old forest species.

COHESION–TENSION THEORY AND XYLEM DYSFUNCTION

The cohesion–tension (C–T) theory was proposed more than 100 years ago by Dixon and

Joly (1894), and some aspects of the C–T theory were put on a quantitative basis by van

den Honert (1948) with the introduction of the Ohm’s law analog of sap flow in the

soil–plant–atmosphere continuum.

WATER TRANSPORT UNDER NEGATIVE PRESSURE

According to the C–T theory, water ascends plants in a metastable state under tension, that is,

with xylem pressure (P

) more negative than that of a perfect vacuum. The driving force is

generated by surface tension at the evaporating surfaces of the leaf, and the tension is

transmitted through a continuous water column from the leaves to the root apices and

throughout all parts of the apoplast in every organ of the plant. Evaporation occurs predomi-

nately from the cell walls of the substomatal chambers due to the much lower water potential

of the water vapor in air. The evaporation creates a curvature in the water menisci of

apoplastic water within the cellulosic microfibril pores of cell wall. Surface tension forces

consequently lower P

in the liquid directly behind the menisci (the air–water interfaces). This

creates a lower water potential, C, in adjacent regions, including adjoining cell walls and cell

protoplasts. The lowering of C is a direct consequence of P

which is one of the two major

components of water potential in plants, the other component is the solute potential p (see

Equation 6.5 through Equation 6.7). The energy for the evaporation process ultimately comes

from the sun, which provides the energy to overcome the latent heat of evaporation of the

water molecules; that is, the energy to break hydrogen bonds at the menisci.

This tension (negative P

) is ultimately transferred to the roots, where it lowers C of the

roots below the C of the soil water. This causes water uptake from the soil to the roots and

from the roots to the leaves to replace water evaporated at the surface of the leaves. The

Scholander–Hammel pressure bomb (Scholander et al. 1965) is one of the most frequently

used tools for estimating P

. Typically, P

can range down to 2 MPa (in crop plants) or

to 4 MPa (in aridzone species), and in some cases 10 MPa (in California chaparral

species). Readers interested in learning more about the C–T theory of sap ascent and recent

experimental proofs should refer to the report by Tyree (1997), Wei et al. (1999, 2000), and

Tyree and Zimmermann (2002).

CAVITATION,EMBOLISM, AND STABILITY OF BUBBLES

Water in xylem conduits is said to be in a metastable condition when P

is below the pressure

of a perfect vacuum, because the continuity of the water column, once broken, will not rejoin

until P

rise to values above that of vacuum. Metastable conditions are maintained by the

cohesion of water to water and by adhesion of water to wall of xylem conduits. Both cohesion

and adhesion of water are manifestations of hydrogen bonding. Although air–water

interfaces can exist anywhere along the path of water movement, the small diameter of

pores in cell walls and the capillary forces produced by surface tension within such pores

prevent the passage of air into conduits under normal circumstances. When P

becomes

negative enough, the continuity of the water column in the conduit is rapidly broken, which is

Francisco Pugnaire/Functional Plant Ecology 7488_C006 Final Proof page 197 10.5.2007 2:47pm Compositor Name: VBalamugundan

Water Relations and Hydraulic Architecture 197

called a cavitation event. Water is drawn out of cavitated conduits by surrounding tissue,

leaving a void filled with water vapor. Eventually, air diffuses into the void; when this

happens, the conduit is said to be embolized.

A cavitation event in xylem conduits ultimately results in dysfunction. A cavitation occurs

when a void of sufficient radius forms in water under tension. The void is filled with gas

(water vapor and some air) and is inherently unstable, that is, surface tension forces makes it

spontaneously collapse unless the water is under sufficient tension (negative pressure) to make

it expand.

The chemical force driving the collapse is the energy stored in hydrogen bonds, the

intermolecular force between adjacent water molecules. In ice, water is bound to adjacent

water molecules by four hydrogen bonds. In the liquid state, each water molecule is bound by

an average of 3.8 hydrogen bonds at room temperature. In the liquid state, hydrogen bonds

are forming and breaking all the time, permitting more motion of molecules than in ice

(Slatyer 1967). However, when an interface between water and air is formed, some of those

hydrogen bounds are broken and the water molecules at the surface are at a higher energy

state because of the broken bonds. The force (N ¼Newtons) exerted at the interface as

hydrogen bonds break and reform can be expressed in pressure units (Pa) because pressure

is dimensionally equal to energy (J ¼Joules) per unit volume of molecules, that is,

3

¼Nmm

3

¼Nm

2

¼Pa. Stable voids in water tend to form spheres because spheres

have the least surface area per unit volume, and thus a spherical void has the minimum

number of broken hydrogen bonds per unit volume of void. The pressure tending to make a

void collapse is given by 2t=r, where r is the radius of the spherical void and t is the surface

tension of water (¼0.072 Pa m at 258 C).

For a void to be stable, its collapse pressure (2t=r) must be balanced by a pressure

difference across its surface or meniscus ¼P

P

,whereP

is the absolute pressure (¼P

the atmospheric pressure) of the water and P

is the absolute pressure of the void.

P

¼ 2t=r: (6:22)

is always above absolute zero pressure (¼perfect vacuum) since the void is usually filled

with water vapor and some air. Relatively stable voids are commonplace in daily life, for

example, the air bubbles that form in a cold glass of water freshly drawn from a tap. An

entrapped air bubble is temporarily stable in a glass of water because P

is a relatively

constant 0.1 MPa, and P

is determined by the ideal gas law, P

¼nRT=V, where n is the

number of moles of air in the bubble, R is gas constant, T is absolute temperature, and V is

the volume of the bubble. The tendency of the void to collapse (2t=r) makes V decrease, which

causes P

to increase according to the ideal gas law because P

is inversely proportional to V.

The rise in P

provides the restoring force across the meniscus needed for stability. However,

an air bubble in a glass of water is only temporarily stable, because according to Henry’s law,

the solubility of a gas in water increases with the pressure of the gas. Therefore, the increased

pressure exerted by 2t=r makes the gas in the bubble more soluble in water, and it slowly

collapses as the air dissolves, that is, as n decreases.

Air bubbles are rarely stable in xylem conduits because transpiration can draw P

to values

less than zero. As P

falls toward zero, the bubble expands according to the ideal gas law, but

because V can never grow larger than the volume of the conduit, P

can never fall to or below

zero to permit P

– P

to balance 2t=r without a decline in P

. Once the bubble has expanded to

fill the lumen, the conduit is dysfunctional and no longer capable of transporting water.

Fortunately for the plant, a dynamic balance at the meniscus in cell walls is ultimately achieved.

This stability is discussed subsequently, first in the context of a vessel and its pit membranes.

As the air bubble is drawn up to the surface of the pit membrane in vessel cell walls, the

pores in the pit-membrane break the meniscus into many small menisci at the opening of each

Francisco Pugnaire/Functional Plant Ecology 7488_C006 Final Proof page 198 10.5.2007 2:47pm Compositor Name: VBalamugundan

198 Functional Plant Ecology

pore. As the meniscus is drawn through the pores, the radius of curvature of the meniscus, r

falls toward the radius of the pores, r

. As long as r

exceeds r

, the necessary conditions for

stability are again achieved, that is,

P

¼ 2t=r

: (6:23)

Usually, a dysfunctional conduit eventually fills with air at atmospheric pressure (as

demanded by Henry’s law); therefore, P

eventually approaches 0.1 MPa as gas diffuses

through water to the lumen and comes out of solution. When P

equals 0.1 MPa, the conduit

is said to be fully embolized. As P

rises and falls as dictated by the demands of transpiration,

adjusts at the pit-membrane pores to achieve stability. When the conduit is fully embo-

lized, both sides of Equation 6.23 can be expressed in terms of xylem pressure potential,

¼(P

P

) ¼2t=r

: (6:24)

The minimum P

that can be balanced by the meniscus is given when r

equals the radius of

the biggest pit-membrane pore bordering the embolized conduit. If the biggest pore is 0.1 or

0.05 mm, then the minimum stable P

is 1.44 or 2.88 MPa, respectively. The porosity of

the pit membrane is therefore critical to preventing dysfunction of vessels adjacent to

embolized vessels (Sperry and Tyree 1988). When P

falls below the critical value, the air

bubble is sucked into an adjacent vessel, seeding a new cavitation.

Consequently, the genetics that determines pit morphology and pit-membrane porosity

must be under strong selective pressure. A safe pit membrane is one with very narrow pores

and thick enough and thus strong enough to sustain substantial pressure differences without

rupturing. Recently substantial advances have been made in the above issues and readers

should consult Sperry and Hacke (2004a,b), Hacke et al. (2004), and Wheeler et al. (2005).

The situation for tracheids of conifers is different because air movement from an

embolized tracheid to an adjacent tracheid is prevented by the sealing (aspiration) of the torus

against the overarching border of the pit. The porosity of the margo that supports the

torus is too large to prevent meniscus passage at pressure difference exceeding 0.1 MPa in

most cases (Sperry and Tyree 1990). However, because the margo is elastic, a pressure

difference of just 0.03 MPa is sufficient to deflect the torus into the sealed position. Air

bubbles pass between tracheids when the pressure difference becomes large enough to rip the

torus out of its sealed position (Sperry and Tyree 1990).

VULNERABILITY CURVES AND THE AIR-SEEDING HYPOTHESIS

Water movement can occur at night or during rain when P

is positive in some plants due to

root pressure, that is, osmotically driven flow from roots. Water flow under positive P

often accompanied by gutation, that is, the formation of water droplet at leaf margins as

frequently seen in many bamboo species. However, water is normally under negative pressure

(tension) as it moves through the xylem toward the leaves during sunny days. The water is

thus in a metastable condition and vulnerable to cavitation due to air entry into the water

columns. Cavitation results in embolism (air blockage), thus disrupting the flow of water

(Tyree and Sperry 1989). Cavitation in plants can result from water stress, and each species

has a characteristic vulnerability curve, which is a plot of the percent loss k

in stems versus

the xylem pressure potential, P

, required to induce the loss. Vulnerability curves are typically

measured by dehydrating large excised branches to known P

. Stem segments are then cut

under water from the dehydrated branches; the air bubbles remain inside the conduits for the

most part. An initial conductivity measurement is made and compared with the maximum K

after air bubbles have been dissolved. Recently Cohcard et al. (2005) have invented a very

Francisco Pugnaire/Functional Plant Ecology 7488_C006 Final Proof page 199 10.5.2007 2:47pm Compositor Name: VBalamugundan

Water Relations and Hydraulic Architecture 199