Roy K.K. Potential theory in applied geophysics
Подождите немного. Документ загружается.


13.7 Oscillating Horizontal Magnetic Dipole Placed on the Surface 409
Fig. 13.10. Horizontal oscillating magnetic dipole on the surface of the earth
Π=a
x
Π
x
+ a
z
Π
z
(13.163)
i.e.
Π must have two components
Π
x
and
Π
z
.
In this problem the plane of symmetry is the X - Z plane (Fig. 13.10) and the
axis of symmetry does not exist. Therefore the wave equation is
∂
2
Π
∂ρ
2
+
1
ρ
∂
Π
∂ρ
+
1
ρ
2
∂
2
Π
∂ψ
2
+
∂
2
Π
∂z
2
= γ
2
Π (13.164)
in cylindrical polar coordinate and
Π=f(ρ, ψ, z). Using the method of sepa-
ration of variables we can write
Π=R(ρ)Ψ(ψ) Z (z) (13.165)
Now let
1
Ψ
d
2
Ψ
dψ
2
= −m
2
(13.166)
1
Z
d
2
Z
dz
2
=n
2
+ γ
2
(13.167)
Substituting in (13.164) we get
1
R
d
2
R
dρ
2
+
1
Rρ
dR
dρ
+
n
2
−
m
2
ρ
2
R = 0 (13.168)
The solutions are
(a) cos mψ sin mψ
(b) e
±z
√
n
2
+γ
2
(c) J
m
(nρ), Y
m
(nρ) (13.169)
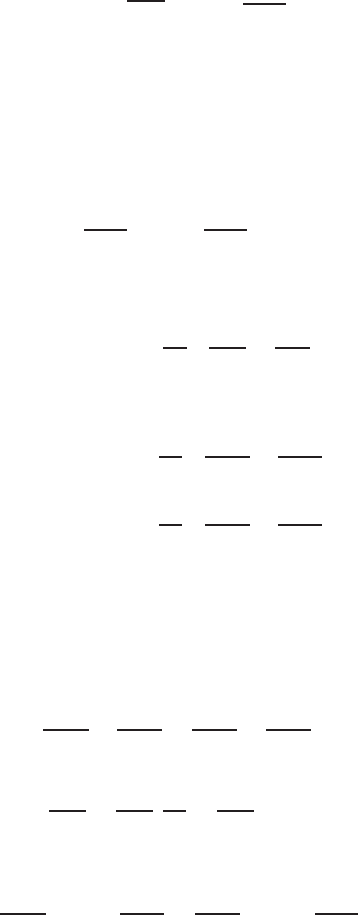
410 13 Electromagnetic Wave Propagation
Since x z plane is a plane of symmetry, therefore cos mψ is a solution and sin
mψ can not be a solution. As a result the expression for the vector potential is
Π=
α
m=0
α
0
cos mψ
f
n
e
−z
√
n
2
+γ
2
+g
n
e
z
√
n
2
+γ
2
J
m
(nρ)dn. (13.170)
Because Y
m
(n, ρ) is no t a good potential function as discussed in Chap. 7. It
is assumed that
Π
x
behave in a similar way as
Π
z
behavedinthecaseofa
vertical oscillating electromagnetic dipole (Sect. 13.3). So the vector potential
will be independent of the azimuthal angle ψ and m will be zero. The general
solution for
Π
x
will be
Π
x
=
α
0
f
n
e
−z
√
n
2
+γ
2
+g
n
e
z
√
n
2
+γ
2
J
0
(nρ)dn. (13.171)
Since
E
x
= −γ
2
Π
x
+
∂
∂x
∂
Π
x
∂x
+
∂
Π
z
∂z
(13.172)
We can write the x component of the electric field in the two media as follows.
E
0x
= −γ
2
0
Π
0x
+
∂
∂x
∂
Π
0x
∂x
+
∂
Π
0z
∂z
(13.173)
E
1x
= −γ
2
1
Π
1x
+
∂
∂x
∂
Π
1x
∂x
+
∂
Π
1z
∂z
. (13.174)
Since the tangential component of the electric field is continuous across the
boundary we get
E
0x
=
E
1x
at z = 0,
γ
2
0
Π
0x
= γ
2
1
Π
1x
(13.175)
∂
Π
0x
∂x
+
∂
Π
0z
∂z
=
∂
Π
1x
∂x
+
∂
Π
1z
∂z
. (13.176)
Since
∂
Π
x
∂x
=
∂
Π
x
∂ρ
.
∂ρ
∂x
=
∂
Π
x
∂ρ
cos ψ
1
(13.177)
(13.176) can be written as
∂
Π
0x
∂ρ
cos ψ +
∂
Π
0z
∂z
=
∂
Π
1x
∂ρ
cos ψ +
∂
Π
1z
∂z
(13.178)
In order to apply the boundary condition, we have to equate the coefficient of
cos ψ on both the sides. Therefore
Π
z
must have a cos ψ term. Since the source

13.7 Oscillating Horizontal Magnetic Dipole Placed on the Surface 411
potential has cos ψ terms, the perturbation potential will also have the cos ψ
terms. Therefore m = 1, for the z component of the perturbation potential
and it will be
Π
z
=cosψ
α
0
p
n
e
−z
√
n
2
+γ
2
+ q
n
e
z
√
n
2
+γ
2
J
1
(nρ) dn. (13.179)
Since the source potential is
me
−γr
r
where r = (z − h)
2
+ ρ
2
or (h − z)
2
+ ρ
2
depen d i n g upon whether z is greater or less than h. The vector potentials in
the first and second media can be written following the procedure laid down
in the previous problem as
Π
0x
=m
α
0
n
n
0
e
−|h−z|n
0
/J
0
(nρ) dn
+
α
0
f
n
e
−n
0
z
J
0
(nρ) dn (13.180)
Π
1x
=
α
0
g
n
e
n
1
z
J
0
(nρ) dn (13.181)
Here
n
2
0
=n
2
+ γ
2
0
and
n
2
1
=n
2
+ γ
2
1
. (13.182)
The z component vector potentials are
Π
0z
=cosψ
α
0
p
n
e
−n
0
z
J
1
(nρ) dn (13.183)
Π
1z
=cosψ
α
0
q
n
e
n
1
z
J
1
(nρ) dn. (13.184)
In this problem
E
x
= −γ
2
Π
x
+
∂
∂x
∂
Π
x
∂x
+
∂
Π
z
∂z
(13.185)
E
y
=
∂
∂y
∂
Π
x
∂x
+
∂
Π
z
∂z
(13.186)
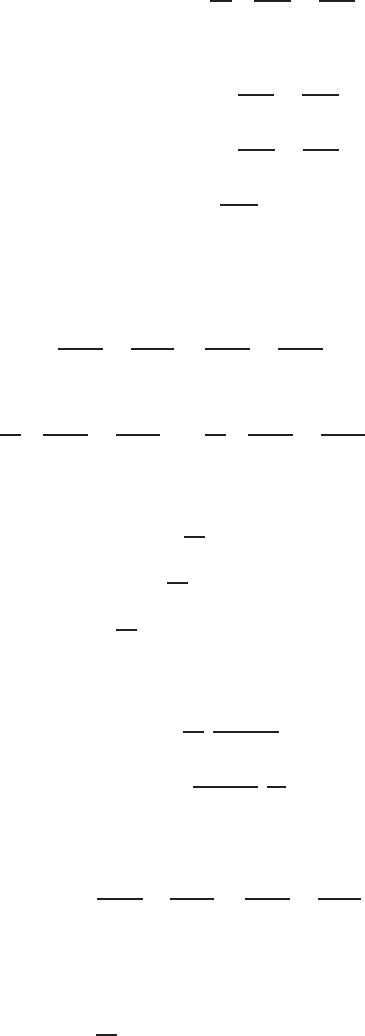
412 13 Electromagnetic Wave Propagation
E
z
= −γ
2
Π
z
+
∂
∂z
∂
Π
x
∂x
+
∂
Π
z
∂z
. (13.187)
H
x
=(σ +iω ∈)curlΠ
x
=(σ +iω ∈)
∂Π
z
∂y
−
∂Π
y
∂z
(13.188)
H
y
=(σ +iω ∈)
∂Π
x
∂z
−
∂Π
z
∂x
(13.189)
H
z
=(σ +iω ∈)
∂Π
x
∂y
. (13.190)
The boundary conditions are
γ
2
0
Π
0x
= γ
2
1
Π
1x
(13.191)
∂
Π
0x
∂x
+
∂
Π
0z
∂z
=
∂
Π
1x
∂x
+
∂
Π
1x
∂z
(13.192)
γ
2
0
Π
oz
= γ
2
1
Π
1z
(13.193)
γ
2
0
µ
0
∂Π
0x
∂z
−
∂Π
0z
∂x
=
γ
2
1
µ
1
∂Π
1x
∂z
−
∂Π
1z
∂x
. (13.194)
Applying these boundary conditions, we get
m.
n
n
0
e
−n
0
h
+f
n
=g
n
(13.195)
γ
2
0
m.
n
n
0
e
−hn
0
+ γ
2
0
f
n
= γ
2
1
g
n
(13.196)
γ
2
0
m.
n
n
0
.n
0
e
−hn
0
− γ
2
0
.n
0
f
n
= γ
2
1
n
1
g
n
. (13.197)
Using these boundary conditions, f
n
and g
n
can be obtained as
f
n
=m.
n
n
0
.
n
0
− n
1
n
0
+n
1
e
−n
0
h
(13.198)
g
n
=2m.
n
n
0
+n
1
.
γ
2
0
γ
2
1
.e
−n
0
h
. (13.199)
Using the other boundary conditions i.e.,
∂
Π
0x
∂x
+
∂
Π
0z
∂z
=
∂
Π
1x
∂x
+
∂
Π
1z
∂z
and
γ
2
0
Π
0z
= γ
2
1
Π
1z
,
we get
m.
n
n
0
e
−n
0
h
.n+f
n
− n
0
p=ng+n
1
.q (13.200)

13.7 Oscillating Horizontal Magnetic Dipole Placed on the Surface 413
and
γ
2
0
p=γ
2
1
g (13.201)
and
p=m.
2n
2
n
0
+n
1
.
γ
2
0
− γ
2
1
n
0
γ
2
1
+n
1
γ
2
0
.e
−n
0
h
q=m.
2n
2
n
0
+n
1
.
γ
2
0
γ
2
1
.
γ
2
0
− γ
2
1
n
0
γ
2
1
+n
1
γ
2
0
e
−n
0
h
. (13.202)
Once all the constants are determined applying the boun d ary conditions,
the expression for the vector potential can be determined.
When we bring the horizontal magnetic dipole on the surface of the earth i.e.,
h=0
We get
p=2m
n
n
0
+n
1
.
γ
2
0
γ
2
1
(13.203)
and
q=m.
2n
2
n
0
+ n
1
.
γ
2
0
γ
2
1
γ
2
0
− γ
2
1
n
0
γ
2
1
+ n
1
γ
2
0
. (13.204)
Therefore
Π
1x
=2m
α
0
n
n
0
+n
1
.
γ
2
0
γ
2
1
.e
n
1
z
J
0
(nρ)dn (13.205)
and
Π
1z
=2m cos ψ
α
0
n
2
n
0
+ n
1
.
γ
2
0
γ
2
1
.
γ
2
0
− γ
2
1
n
0
γ
2
1
+ n
1
γ
2
0
e
−n
1
z
J
1
(nρ) dn (13.206)
since
m=
I.dx
4π (σ +iω ∈)
=
Idx
4π
.
iωµ
γ
2
0
. (13.207)
γ
0
is negligibly small in comparison to γ
1
(i.e. conductivity of the air in neg-
ligible in comparison to that of the earth) (13.205) and 13.206). We get
Π
1x
=
Idx
2π
.
iωµ
γ
2
1
α
0
n
n+n
1
e
n
1
z
J
0
(nρ) dn (13.208)
Π
1z
= −
Idx
2π
.
iωμ
γ
2
1
, cos ψ
α
0
n
n + n
1
e
n,z
J
1
(nρ) dn (13.209)
since
∂
∂ρ
(J
0
(nρ)=−nJ
1
(nρ)
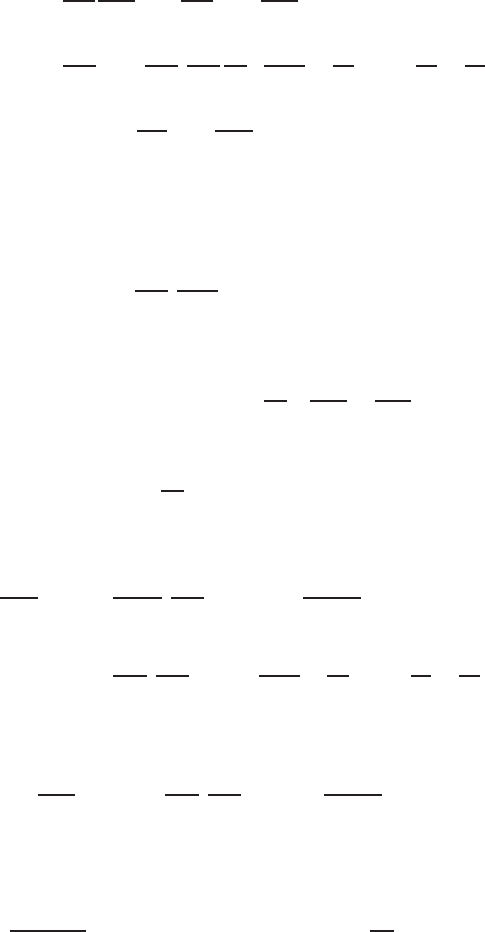
414 13 Electromagnetic Wave Propagation
The expression for H
z
is
H
z
= −
γ
2
iωµ
∂
Π
x
∂y
= −
γ
2
iωµ
sin ψ
∂Π
x
∂ρ
(13.210)
= −
γ
2
iωμ
sin ψ
Idx
2π
.
iωμ
γ
2
∂
∂ρ
1
γ
2
ρ
3
−
1
γ
2
e
−γρ
1
ρ
3
+
γ
ρ
2
⇒
H
z
= −
Idx
2π
sin ψ
1
γ
2
ρ
4
3 − e
−γρ
3+3γρ + γ
2
ρ
2
. (13.211)
When ψ =0,
H
z
= 0 i.e., there cannot be any vertical magnetic field along the
horizontal axis of the vertical magnetic dipole. H
z
is maximum when ψ = π/2
i.e., along the Y axis we get
H
z
|
max
= −
Idx
2π
.
1
γ
2
ρ
4
'
3 −e
−γρ
3+3γρ + γ
2
ρ
2
(
. (13.212)
The electric field is
E
x
= −γ
2
Π
x
+
∂
∂x
∂
Π
x
∂x
+
∂
Π
z
∂z
. (13.213)
Since
∂
∂ρ
(J
0
(nρ) dn) = −nJ
1
(nρ)
We can write
∂
Π
x
∂x
z=0
=
−
Idx
2π
.
iωμ
γ
2
. cos ψ
α
0
−
n
n + n
1
J
1
(nρ) dn
=
Idx
2π
.
iωμ
γ
2
. cos ψ
1
γ
2
ρ
3
−
1
γ
2
e
−γρ
1
ρ
3
+
γ
ρ
2
. (13.214)
Similarly
∂Π
z
∂z
z=0
= −
Idx
2π
.
iωμ
γ
2
. cos ψ
α
0
nn
1
n + n
1
J
1
(nρ) dn. (13.215)
Adding (13.214) and (13.215), the integral part reduces to
α
0
n
2
+nn
1
n+n
1
J
1
(nρ)dn=
α
0
nJ
1
(nρ)dn=−
∂
∂ρ
α
0
J
0
(nρ)dn. (13.216)
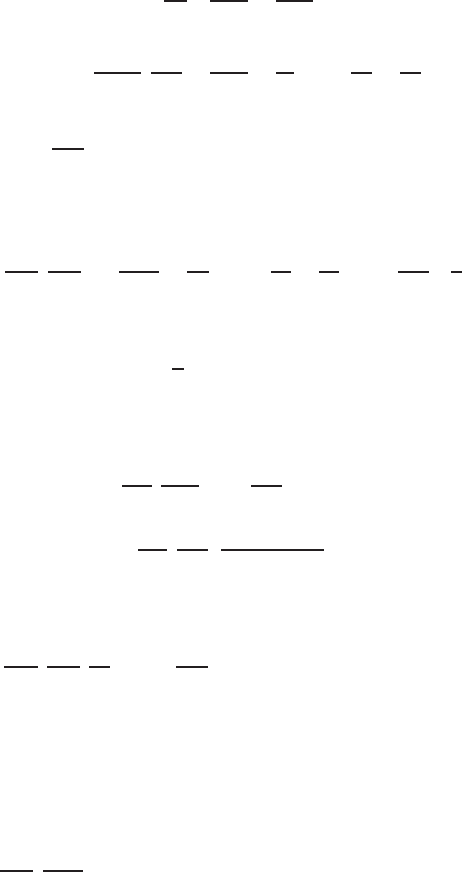
13.7 Oscillating Horizontal Magnetic Dipole Placed on the Surface 415
Therefore
E
x
= −γ
2
Π
x
+
∂
∂ρ
∂
Π
x
∂x
+
∂
Π
z
∂z
cos ψ (13.217)
E
z
= −
γ
2
Idx
2π
.
iωµ
γ
2
.
1
γ
2
ρ
3
−
1
γ
2
e
−γρ
1
ρ
3
−
γ
ρ
2
+
∂
2
∂ρ
2
α
0
J
0
(nρ) dn cos
2
ψ (13.218)
Now taking
E
x
= −
Idx
2π
.
iωμ
γ
2
.
1
γ
2
ρ
3
−
1
γ
2
e
−γρ
1
ρ
3
−
γ
ρ
2
+
∂
2
∂ρ
2
1
ρ
(13.219)
where
1
ρ
=
α
0
J
0
(nρ)dn.
Equation (13.219) simplifies down to
E
x
=
Idx
2π
.
iωµ
γ
2
ρ
3
2 −
3x
2
ρ
2
− e
−γρ
(1 + γρ)
(13.220)
E
y
= −
Idx
2π
.
iωµ
γ
2
,
3sinψ cos ψ
ρ
3
. (13.221)
We can express the electrical components in
E
ψ
and
E
ρ
in the form
E
ρ
= −
Idx
2π
.
iωμ
γ
2
.
1
ρ
3
2 −
3x
2
ρ
2
− e
−γρ
(1 + γρ)
cos ψ +sin
2
ψ cos ψ
(
.
(13.222)
For ψ =90
0
, i.e., in the broad side po sition there will be no radial component
of the electric field and the magnetic field will be maximum.
Now
E
ρ
=E
y
cos ψ +E
x
sin ψ
= −
Idx
2π
.
iωμ
γ
2
ρ
3
'
−
5
2 −3cosφ − e
−γρ
(1 + γρ)
6
sin ψ +3cos
2
ψ sin ψ
(
.
(13.223)
E
ψ
=E
y
cos ψ − E
x
sin ψ. (13.224)
When ψ =90
0
416 13 Electromagnetic Wave Propagation
E
ψ
=
Idx
2π
.
iωµ
γ
2
.
1
ρ
3
.
'
2 −e
−γρ
(1 + γρ)
(
, (13.225)
H
z
=
Idx
2π
.
iωµ
γ
2
.
1
ρ
4
.
'
3 −e
−γρ
3+3γρ + γ
2
ρ
2
(
(13.226)
and
E
ρ
=0. (13.227)
Thus both
E
ψ
and
H
z
have maximum values at the broad side position.
Case I: When γρ << 1
H
z
=
Idx
2π
.
3
ρ
2
, Eψ =
Idx
2πσ
.
1
ρ
3
(Static Case). (13.228)
Case II: When γρ >> 1 in the radiation zone
H
z
= −
Idx
2π
.
1
γ
2
ρ
4
.γ
2
ρ
2
.e
−γρ
= −
Idx
2π
.
1
ρ
2
e
−γρ
(13.229)
E
ρ
=
Idx
2π
.
1
γ
2
ρ
4
.γ
2
ρ
2
.e
−γρ
= −
Idx
2π
.
1
ρ
2
e
−γρ
E
ψ
= −
Idxγρ
2πγ
2
.
e
−γρ
ρ
3
−
Idx
2πγ
.
e
−γρ
ρ
2
= −
Idx
2π
.
1
a+ib
.
e
−aρ
ρ
2
.e
−ibρ
. (13.230)
ReE
ψ
= −
Idx
2π
.
1
√
a
2
+b
2
.
e
−αρ
ρ
2
cos
ωt −bρ − tan
−1
b
a
. (13.231)
Thus finally we can define the impedance Z, which is g iven by
Z=
E
ψ
H
z
=
1
√
ωµρ
. (13.232)
Thus by measuri ng
E
ψ
and
H
z
we can measure the conductivity of the earth.
13.8 Electromagnetic Field due to a Long Line Cable
Placed in an Infinite and Homogenous Medium
An infinitely long line cable is placed along the Z–direction (Fig 13.11). There-
fore the vector potential will also be in the Z-direction, i.e.,
Π=a
z
Π
z
. (13.233)
For an infinitely long line cable,
∂
∂z
=0,
∂
∂ψ
= 0 (13.234)
where ψ is the azimuthal angle.

13.8 Long Line Cable Placed in an Infinite and Homogenous Medium 417
Fig. 13.11. An infinitely long line electrode is place vertically in an homogeneous
and isotropic full space
The wave equation reduces to
∇
2
Π
z
= γ
2
Π
z
(13.235)
⇒
∂
2
Π
z
∂ρ
2
+
1
ρ
∂Π
z
∂ρ
− γ
2
Π
z
=0. (13.236)
The solution of the (13.236) is I
0
(γρ)andK
0
(γρ)whereI
0
and K
0
are the
modified Bessel’s function of zero order and first and second kind. Since I
0
(γρ)
tends to be infinity as ρ → α, therefore the appropriate expression for the
potential is
Π
z
=bK
0
(γρ) . (13.237)
In this problem, the electric field is
E
z
= −γ
2
Π
z
+grad
∂
Π
z
∂z
= −γ
2
Π
z
+
∂
2
Π
z
∂z
2
. (13.238)
Here
E
ρ
=0and
E
ψ
=0. (13.239)
For an infinitely long cable, there is no variation of
E
z
along the Z–axis i.e.
∂
∂z
= 0. Therefore
E
z
= −γ
2
Π
z
. (13.240)
The magnetic field
H=(σ +iω ∈)curl
Π. (13.241)
In this problem
H
ρ
= 0 (13.242)
H
z
= 0 (13.243)

418 13 Electromagnetic Wave Propagation
and
H
ψ
= −(σ +iω ∈)
∂
Π
z
∂ρ
. (13.244)
We can now write
E
z
= −γ
2
bK
0
(γρ) (13.245)
H
ψ
= −(σ +iω ∈)b
∂
∂ρ
K
0
(γρ) . (13.246)
The value of ‘b’ which is still arbitrary can be determined from the magneto-
static analog :
The magnetic field at a point due to a small current element is
H
ψ
=
Idz sin θ
4πr
2
=
Idz
4π
.
1
ρ
2
+z
2
.
ρ
r
. (13.247)
For an infinitely long line cable
H
ψ
=
α
−α
Idz
4π
.
ρ
(ρ
2
+z
2
)
3/2
=
I
4π
.
2
ρ
=
I
2πρ
. (13.248)
Now
E
z
= −γ
2
bK
0
(γρ) (13.249)
H
ψ
= −(σ +iω ∈)bγK
′
0
(γρ)
=(σ +iω ∈)bγk
1
(γρ) . (13.250)
We know
K
0
(z) = −ln
zc
2
I
0
(z) +
∞
m=1
z
2m
2
2m
(m!)
2
1+
1
2
+
1
3
+ .....
1
m
(13.251)
where c is a constant a nd has some definite value.
K
′
0
(z) = −
1
z
I
0
(z) −ln
zc
2
I
′
0
(z) +
∂
∂z
∞
m=1
z
2m
2
2m
(m!)
2
1+
1
2
+
1
3
+ .....
1
m
.
(13.252)
Now the value of
I
0
(z) =
z
2m
2
2m
(m!)
2
=1+
z
2
2
2
+
z
4
2
4
(2!)
2
+ ....... (13.253)
Since
Lim
z→0
K
′
0
(z) = −
1
z
, (13.254)
