Roy K.K. Potential theory in applied geophysics
Подождите немного. Документ загружается.


13.4 Magnetotelluric Response for a La yered Earth Model 389
13.4 Magnetotelluric Response for a Layered
Earth Mo del
For a homogeneous, earth, the wave equation is given by
∇
2
E = μσ
∂E
∂t
+ μ ∈
∂
2
E
∂t
2
. (13.43)
Component of the wave equation (13.43) changes to the form
∂
2
E
x
∂x
2
+
∂
2
E
x
∂y
2
+
∂
2
E
x
∂z
2
= µσ
∂E
x
∂t
+ µ ∈
∂
2
E
x
∂t
2
. (13.44)
For a plane electromagnetic wave propagating along the z direction (for a
harmonicall y varying field) is given by
∂
2
E
x
∂z
2
= γ
2
E
x
where γ
2
=iωµ(σ +iω ∈). (13.45)
From (13.45), we get
E
x
=Ae
γz
+Be
−γz
. (13.46)
For a homogeneous earth E
x
vanishes at Z →∞. This condition puts
A=0and E
x
=Be
−γz
. (13.47)
Here E
x
is time varying (E
x
(e
iωt
)) and generates a time variant orthogo-
nal magnetic field in the y direction. The vertical component H
z
=0.From
Maxwell’s equation,
curl
E
y
= −iωµ
H
y
. (13.48)
For an uniform field
∂E
x
∂z
= −iωµH
y
(13.49)
H
y
= −
γ
iωµ
Be
−γz
. (13.50)
Therefore Cagniard impedance for a homogeneous ground is
Z=
E
x
H
y
=
iωµ
γ
. (13.51)
At low frequency γ =
√
iωµσ,Z=
√
ωµρe
iπ/4
and
ρ =
1
ωµ
E
x
H
y
2
(13.52)
390 13 Electromagnetic Wave Propagation
or
ρ =0.2T
E
x
H
y
2
. (13.53)
For a two layer earth model with layer resistivities ρ
1
and ρ
2
and thickness
h
1
, the electrical and magnetic components can be written as
E
x
=Ae
γx
+Be
−γx
(13.54)
H
y
= −
γ
iωµ
Ae
+γx
− Be
−γx
. (13.55)
The ratio of E
x
and H
y
yields
E
x
H
y
= −
iωμ
γ
Ae
γz
+ Be
−γz
Ae
γz
− Be
−γz
(13.56)
Dividing the numerator and the denominator by
√
AB, substituting
0
A
B
=exp
ln
0
A
B
.
We can rewrite the relation as
E
x
H
y
= −
iωµ
γ
exp
γz+ln
A
B
+exp
−γz −ln
A
B
exp
γz+ln
A
B
− exp
−γz −ln
A
B
= −
iωµ
γ
Coth
γz+ln
0
A
B
. (13.57)
We determine the ratio of wave impedances at two different depths to elimi-
nate A and B. For this purpose we evaluate Z
2
at a depth z
2
with reference to
Z
1
at a depth z
1
such that z
1
and z
2
are in the same medium. The impedance
Z
1
at a depth z
1
is given as
Z
1
= −
iωµ
γ
Coth
γz
1
+ln
0
A
B
. (13.58)
From (13.58) we get
ln
0
A
B
= −
Coth
−1
Z
1
γ
iωµ
+ γz
1
. (13.59)
The impedance Z
2
at a depth z
2
is
Z
2
= −
iωµ
γ
Coth
γ (z
2
− z
1
) −Coth
−1
γz
1
iωµ
. (13.60)

13.4 Magnetotelluric Response for a La yered Earth Model 391
This equation is valid as long as Z
1
and Z
2
are in same medium. If we put
z
2
=0,thenz
2
− z
1
=h
1
, i.e., thickness of the top layer, then we have Z
2
at
the ground surface z = 0.
Z
2
(z
2
=0)=
iωµ
γ
Coth
5
γh
1
+Coth
−1
6
γz
1
iωµ
. (13.61)
If we now let h
1
→∞, the geologic structure assumes a homogeneous ground
and the (13.60) reduces to
Z
2
=
iωµ
γ
. (13.62)
For a t wo layer earth, we write Z
2
at a depth z = h
1
but in the second medium
and equate it with Z
1
at the same depth. Thus we get
Z
2
=
iωµ
γ
2
Coth
γ
2
∞ +Coth
−1
γ
2
Z
1
iωµ
(13.63)
=
iωµ
γ
2
γ
2
Z
1
iωµ
=Z
1
.
In the first medium, we have
Z
0
=
iωµ
γ
1
Coth
γ
1
h
1
+Coth
−1
γ
1
Z
1
iωµ
. (13.64)
Substituting the value of Z
1
from (13.62) to (13.63) we get
Z
0
=
iωµ
γ
1
Coth
γ
1
h
1
+Coth
−1
γ
1
γ
2
. (13.65)
In a similar manner, we can write the impedance for a three layer earth on
the ground surface as
Z
0
=
iωµ
γ
1
Coth
γ
1
h
1
+Coth
−1
γ
1
γ
2
Coth
γ
2
h
2
+Coth
−1
γ
2
γ
1
. (13.66)
The general expression for impedance for an N-layered earth is (from (13.65))
(Fig. 13.3)
Z
0
=
iωµ
γ
1
Coth
γ
1
h
1
− Coth
−1
γ
1
γ
2
Coth
γ
2
h
2
+Coth
−1
γ
2
γ
3
...........+Coth
−1
γ
n−2
γ
n−1
Coth
γ
n−2
h
n−1
+Coth
−1
γ
n−1
γ
n−2
.
(13.67)
Equation (13.66) is one of the approaches for computation of one dimensional
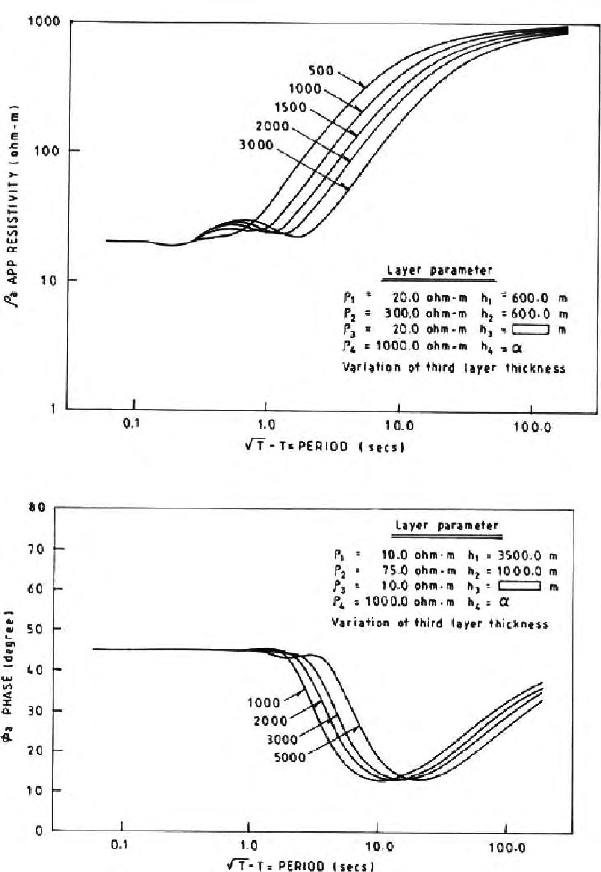
magnetotelluric response for an N-layered earth (Fig. 13.4 and Fig. 13.5).

392 13 Electromagnetic Wave Propagation
Fig. 13.4. Magnetotelluric apparent resistivity and phase variations with period;
theoretical model parameter values are given in the diagrams
13.4 Magnetotelluric Response for a La yered Earth Model 393
Fig. 13.5. Magnetotelluric apparent resistivity and phase variations with
period;model parameters are given in the diagram
394 13 Electromagnetic Wave Propagation
13.5 Electromagnetic Field due to a Vertical Oscillating
Electric Dipole
A small oscillating electric dipole is assumed in an infinite full space. The
electromagnetic waves will propagate in all the directions as if a point source is
located at the centre (Fig. 13.6). Therefore, overall potential distribution will
have spherical symmetry and the Laplacian op erator ∇
2
will be i n spherical
coordinate and it will be a function of ‘r’ the radial direction only.
Let as assume that the Hertz vector
Π has only z-component and is
expressed as
Π
z
= a
z
Π
z
. (13.68)
The wave equation ∇
2
Π
z
= γ
2
Π
z
reduces to the form
∂
2
Π
z
∂r
2
+
2
r
∂Π
z
∂r
= γ
2
Π
z
⇒
∂
2
∂r
2
r
Π
z
= γ
2
r
Π
z
(13.69)
⇒ r
Π
z
=ae
γr
+be
−γr
⇒
Π
z
=
ae
γr
r
+
be
−γr
r
. (13.70)
In an infinite and homogenous medium, there is no possibility for a wave to
be reflected back. The potential will die down with distance. Therefore the
term
ae
γr
r
cannot be a potential function. The correct term is
Π
z
=
be
−γr
r
. (13.71)
The vector p otential for an electromagnetic field changes to
Π
z
=
b
r
for γ =0
i.e., for zero frequency. Vector potential in electromagnetics changes to scalar
po tential in direct current field for zero frequency. Frequency dependent Hertz
vector potential die at a faster pace with distance than the frequency inde-
pe n dent scalar potential due to a DC point source. At this moment the value
of ‘b’ is arbitrary.
The connecting relations between Hertz vector and the magnetic and elec-
tric fields can be written as
E
r
= −γ
2
Π
r
+
∂
∂r
div
Π
z
(13.72)
E
θ
= −γ
2
Π
θ
+
∂
r∂ θ
∂
Π
z
∂z
(13.73)
E
ψ
= −γ
2
Π
ψ
+
1
sin θ
∂
∂ψ
∂
Π
z
∂z
. (13.74)

13.5 Electromagnetic Field due to a Vertical Oscillating Electric Dipole 395
Now
Π
r
=
Π
z
cos θ (13.75)
Π
θ
= −
Π
z
sin θ
and
Π
ψ
=0
For oscillating vertical electric dipole,
Π
ψ
=0and
∂
∂ψ
=0whereψ is an
azimuthal angle. Therefore,
H
r
=(σ +iω ∈)
1
rsinθ
∂
∂θ
sin θ
Π
ψ
−
∂
∂ψ
Π
θ
= 0 (13.76)
H
θ
=(σ +iω ∈)
1
sin θ
⎡
⎣
∂
Π
r
∂ψ
− sin θ
∂
r
Π
ψ
∂r
⎤
⎦
= 0 (13.77)
H
φ
=(σ +iω ∈)
1
r
)
∂
∂r
r
Π
θ
−
∂
Π
r
∂θ
*
(13.78)
Since H
r
and H
θ
are zero, therefore E
r
and E
θ
are not zero because electromag-
netic waves are transverse in nature. The magnetic component which exists
is Hψ.
Now
Π
z
=
be
−γr
r
Fig. 13.6. Vertical oscillating electric dipole in a homogeneous full space

396 13 Electromagnetic Wave Propagation
and
∂
Π
z
∂z
=
−
be
−γr
r
2
−
bγ
r
e
−γr
. (13.79)
Hence
−
γ
2
be
−γr
r
cos θ
E
r
= −
r
2
be
−γr
r
cos θ +
∂
∂r
−
b
r
2
e
−γr
−
bγ
r
− e
−γr
cos θ
=be
−γr
cos θ
−
γ
2
r
+
γ
r
2
+
γ
2
r
2
r
3
+
γ
r
2
=
2b cos θ
r
3
(1 + γr) e
−γr
. (13.80)
Exactly in the same way, the value of E
θ
can be found out as
E
θ
=
−γ
2
be
−γr
r
sin θ +
∂
r∂θ
∂
Π
z
∂z
=
bsinθ
r
3
1+γr+γ
2
r
2
e
−γr
(13.81)
and
H
ψ
=(σ +iω ∈)
1
r
∂
∂r
−
γbe
−γr
r
sin θ
−
∂
∂θ
be
−γr
r
cos θ
=(σ + ω ∈)
bsinθ
r
2
(1 + γr) e
−γr
. (13.82)
To assign a certain value to ‘b’ which is quite arbitrary so far, we seek analogy
from the electrostatic and DC conduction case. In the electrostatic and direct
current flow field cases, the potential at a po int at a distance ‘r’ from a dipo le
of charge +q and −q(and+Iand−I as the case may be) separated by a
distance dz are
φ =
qdz
4πε
cos θ
r
2
(electrostatic case) (13.83)
and
φ =
Idl
4πσ
cos θ
r
2
(DC conduction case) (13.84)
E
θ
= −
1
r
∂φ
∂θ
=
qdz
4πε
sin θ
r
3
(electrostatic case) (13.85)
and
E
θ
=
Idl
4πσ
sin θ
r
3
(DC conduction case). (13.86)

13.5 Electromagnetic Field due to a Vertical Oscillating Electric Dipole 397
Therefore, we can write the value of
Π
z
in case of an oscillating electric
dipole as
Π
z
=
Il
4π (σ +iω ∈)
.
e
−γr
r
(13.87)
where b =
Il
4π ( σ+iω∈)
. I is the current strength and l is the length of the current
dipole i.e., the distance between +I and −I. In order to accommodate the time
varying part, σ was replaced by (σ +iω ∈). We can now write the existing
components of the electric and magnetic fields as
E
r
=
Il
4π (σ +iω ∈)
.
2cosθ
r
3
(1 + γr) e
−γr
(13.88)
E
θ
=
Il
4π (σ +iω ∈)
.
sin θ
r
3
1+γr+γ
2
r
2
e
−γr
(13.89)
E
ψ
=
Il
4π
.
sin θ
r
2
(1 + γr) e
−γr
. (13.90)
Special cases
Case 1 when |γr| << 1
This zone is known as the near zone or static zone.
Here
E
r
=
Il
4π (σ +iω ∈)
.
2cosθ
r
3
(13.91)
E
θ
=
Il
4π (σ +iω ∈)
.
sin θ
r
3
(13.92)
and
H
ψ
=
Il
4π
.
sin θ
r
2
. (13.93)
Case II when |γr| >> 1
This is the far zone or the radiation zone. In this case
E
r
=
Ilγ
4π (σ +iω ∈)
.
2cosθ
r
2
e
−γr
(13.94)
E
θ
=
Ilγ
4π (σ +iω ∈)
.
sin θ
r
e
−γr
(13.95)
and
H
ψ
=
Ilγ
4π
.
sin θ
r
.e
−γr
. (13.96)
In this case, the radial component
E
r
is decreasing rapidly with distance, E
θ
and H
ψ
will form a transverse wave at a great distance when
E
r
has become
negligible. Since E
θ
and H
ψ
are in the same plane, the resultant effect will be
a plane transverse wave propagating outward.
398 13 Electromagnetic Wave Propagation
Here
E
θ
H
ψ
=
γ
2
σ +iω ∈
.
1
γ
=
γ
σ +iω ∈
=
0
iωµ
σ +iω ∈
= η (13.97)
is the impedance of the medium. We can express E
θ
as
E
θ
=
Il
4π
.ωµ.
sin θ
r
e
−(α+iβ)
r
.e
iωt
.e
iπ/
2
=
Il
4π
.ωµ.
sin θ
r
e
−αr
.e
i(ωt−βr+π/
2
)
. (13.98)
Since
γ = α +iβ =
α
2
+ β
2
.e
itan−1
(
β
α
)
H
ψ
=
Il
4π
α
2
+ β
2
.
sin θ
r
.e
−αr
.e
i(ωt−β+π/
2
)
. (13.99)
If electrica l conductivity of the medium is zero, then
β = ω
√
µ ∈,
therefore
E
θ
=
Il
4π
.
ωµ sin θ
r
cos (ωt − ω
√
µ ∈.r+π/
2
) (13.100)
and
H
ψ
=
Il
4π
.ω
√
µ ∈.
sin θ
r
cos (ωt − ω
√
µ ∈.r+π/
2
) . (13.101)
(Figs. 13.7 and 13.8). Since there is no phase difference, it is a linearly polar-
ized uniform plane wave and
E
θ
H
ψ
=
ωµ
ω
√
µ ∈
=
0
µ
∈
(13.102)
gives intrinsic impedances of the medium.
Fig. 13.7. Variation of amplitude of the magnetic field H
ψ
with electromagnetic
parameter P(= l
2
ωµσ); l is the distance
