R?ssler U. Solid State Theory: An Introduction
Подождите немного. Документ загружается.


4.3 Occupation Number Representation for Electrons 95
annihilated, while for the second equation it is N + 1 due to the addition of
one particle to |Ψ.
The meaning of occupation numb er representation can be also illustrated
by applying c
†
α
i
c
α
i
to the N-particle state |Ψ. We find
c
†
α
i
c
α
i
|Ψ =(−1)
ν
i
n
α
i
c
†
α
i
|...n
α
i
− 1 ... (4.71)
=(−1)
2ν
i
n
α
i
(1 − (n
α
i
− 1))|...n
α
i
... (4.72)
=
|Ψ n
α
i
=1
0 n
α
i
=0
(4.73)
or in short
c
†
α
i
c
α
i
|Ψ = n
α
i
|Ψ . (4.74)
Thus the eigenvalue of c
†
α
i
c
α
i
is the occupation number n
α
i
of the single-
particle state with quantum numbers α
i
in |Ψ and
ˆ
N =
α
c
†
α
c
α
=
α
ˆn
α
(4.75)
is the number operator with the eigenvalue equation
ˆ
N|Ψ = N |Ψ.
The occupation number or Fock representation allows one to formulate
the system Hamiltonian in terms of creation and annihilation operators. We
give here only the rules for how the one-(
ˆ
A
1
) and two-particle (
ˆ
A
2
)termsof
the Hamiltonian (or any other operator) have to b e rewritten and refer for
details to the Appendix (
A.6):
ˆ
A
1
→
ij
ψ
α
i
|
ˆ
A
1
|ψ
α
j
c
†
α
i
c
α
j
(4.76)
ˆ
A
2
→
ijkl
ψ
(1)
α
i
ψ
(2)
α
j
|
ˆ
A
2
|ψ
(1)
α
l
ψ
(2)
α
k
c
†
α
i
c
†
α
j
c
α
k
c
α
l
. (4.77)
These expressions have an obvious meaning: The one-particle operator
(depending on the co o rdinates of only one particle) replaces a particle with
quantum numbers α
j
by a particle with α
i
, the two-particle or interaction
operator r emoves first a particle in the state α
l
andthenanotheronein
the state α
k
and adds particles in the states α
j
and α
i
.Theweightofthe
operators are matrix elements of the original operators taken with the single-
particle wave functions ψ
α
of an orthonormal set. The upper index (1) and
(2) in the matrix element of the two-particle operator indicates the pairs of
wave functions which have the same coordinates when integrating in p osition
representation.
This concept is now applied to the system of free electrons for which
{c
†
kσ
,c
k
′
σ
′
} = δ
kk
′
δ
σσ
′
(4.78)

96 4 The Free Electron Gas
and
ˆ
N =
kσ
ˆn
kσ
, ˆn
kσ
= c
†
kσ
c
kσ
,ψ
kσ
(x)=
1
√
V
e
ik·r
χ
σ
(s) , (4.79)
where χ
σ
(s) is a Pauli spinor and s denotes the spin variable. The Hamilto-
nian for the jellium model of free electrons (with the jellium term H
+
from
Problem 4.1)
H
jell
=
l
p
2
l
2m
+
1
8πε
0
k,l
k=l
e
2
|r
k
− r
l
|
+ H
+
, (4.80)
can be rewritten (by making use of (
4.76)and(4.77)) with
l
p
2
l
2m
→
kσ
¯h
2
k
2
2m
c
†
kσ
c
kσ
(4.81)
and
k,l
k=l
e
2
4πε
0
|r
k
− r
l
|
→ψ
k
1
σ
1
ψ
k
2
σ
2
|
e
2
4πε
0
|r
1
− r
2
|
|ψ
k
′
1
σ
′
1
ψ
k
′
2
σ
′
2
(4.82)
= δ
σ
1
σ
′
1
δ
σ
2
σ
′
2
k
v
k
δ
k
1
,k
′
1
+k
δ
k
2
,k
′
2
−k
(4.83)
where v
k
= e
2
/ε
0
Vk
2
is the Fourier transform of the Coulomb p otential (see
Appendix). With the replacements σ
1
= σ
′
1
= σ, σ
2
= σ
′
2
= σ
′
and k
′
1
→ p,
k
′
2
→ q we find
H
jell
=
kσ
¯h
2
k
2
2m
c
†
kσ
c
kσ
+
1
2
p,q,k
σσ
′
v
k
c
†
p+kσ
c
†
q−kσ
′
c
qσ
′
c
pσ
+ H
+
. (4.84)
The interaction term becomes divergent for k → 0. However, this diver-
gence is exactly compensated by the jellium term for which we obtained as
solution of Problem 4.1 H
+
= −
1
2
v
0
N
2
while
1
2
p,qσσ
′
v
0
c
†
pσ
c
†
qσ
′
c
qσ
′
c
pσ
=
1
2
v
0
pσ
ˆn
pσ
qσ
′
ˆn
qσ
′
=
1
2
v
0
N
2
. Thus we arrive at the Hamiltonian for free
electrons in the jellium model
H
jell
=
kσ
¯h
2
k
2
2m
c
†
kσ
c
kσ
+
1
2
p,q,k=0
σσ
′
v
k
c
†
p+kσ
c
†
q−kσ
′
c
qσ
′
c
pσ
. (4.85)
Its first term accounts for the single-particle energy of free noninteracting
electrons, while the second term describes the electron–electron interaction.
The interaction term is visualized in Fig. 4.10 as a Feynman diagram with the
solid lines r e presenting incoming and outgoing electrons with their respective

4.4 Hartree–Fock Approximation 97
>
>
q-kσ¢
qσ¢
>
>
p+kσ
k
pσ
Fig. 4.10. Feynman diagram of the electron–electron in teraction. The solid lines
represent propagating electrons, the dashed line the Coulomb potential
wave vector and spin and the dashed line symbolizes the Coulomb interaction.
This Hamiltonian does not only apply to electron systems in vacuum, but
also to those realized in matter (see Table 4.1), however,by replacing the free
electron mass by an effective mass and screening the Coulomb interaction
with the dielectric constant of the matter. Moreover it applies also to electron
systems in energy bands, however, with a matrix element between full Blo ch
states (see Chaps.
5 to 7). In the following sections we develop the concepts
for approximate solutions of the ground state problem for the jellium model.
4.4 Hartree–Fock Approximation
In Sect.
4.1, we have characterized the ground state of the noninteracting
electron system (at T = 0 K) as the filled Fermi sphere. The corresponding
N-particle wave function, that takes into account the Pauli principle, is a
Slater determinant composed of the wave functions of occupied single-particle
states, i.e., plane waves with |k|≤k
F
but it can also be obtained by applying
creation operators to the fermion vacuum to fill the Fermi sphere. Let us
denote this ground state by |Ψ
0
. We may now calculate the expectation value
of H
jell
from (
4.85)with|Ψ
0
giving the ground state energy in Hartree
10
–Fock
(HF) approximation
E
HF
0
= Ψ
0
|H
jell
|Ψ
0
=
kσ
Ψ
0
|
¯h
2
k
2
2m
c
†
kσ
c
kσ
|Ψ
0
+
1
2
k=0
q,p,σσ
′
Ψ
0
|v
k
c
†
p+kσ
c
†
q−kσ
′
c
qσ
′
c
pσ
|Ψ
0
. (4.86)
The first term reproduces the ground state energy
3
5
NE
F
of the noninteracting
electron gas obtained in the Sommerfeld model (Sect.
4.1). The second term
is the first order correction due to the Coulomb interaction, which is treated
10
Douglas Rayner Hartree 1897–1958

98 4 The Free Electron Gas
q
p
q
p
k
F
k
F
direct exchange
Fig. 4.11. Illustration of the direct and exchange terms in the Fermi sphere
here as a perturbation. Before we discuss the quality of this approximation,
this correction has to be calculated. Two contributions, depicted in Fig. 4.11
can be distinguished:
1. Proceeding from right to left the two annihilation operators remove the
electrons with pσ and qσ
′
from the filled Fermi sphere (|Ψ
0
) and the two cre-
ation operators add electrons at p + kσ and q −kσ
′
, respectively. In order to
obtain the filled Fermi sphere (or Ψ
0
|) k has to be zero. However, this term is
excluded from the sum over k in the interaction term as a result of the jellium
model and hence does not modify the ground state energy of the Sommer-
feld model. It should be mentioned, however, that this so-called direct term
describes the electrostatic interaction energy for a system with charge den-
sity n (see Problem 4.1), which becomes important for inhomogenous electron
systems (see Chaps.
5 and 6) and defines the Hartr ee approximation.
2. As before, the two annihilation op erators remove two electrons from the
Fermi sphere, while the two creation operators put them back but now with
interchanged wave vectors. This exchange within the Fermi sphere is possible
only for electrons having the same spin (σ = σ
′
) and whose wave vectors
differ by k = q − p (see Fig. 4.11). This exchange term results from the Pauli
principle and does not have a classical analogue (in contrast with the direct
term). The Hartr ee–Fock approximation is also understo od to have considered
the exchange contribution.
The exchange term is evaluated under the constraints of the exchange
process (k = q − p,σ= σ
′
) giving
E
HF
0
= E
H
0
+
σ,q,p
q=p
e
2
2ε
0
V |q − p|
2
Ψ
0
|c
†
qσ
c
†
pσ
c
qσ
c
pσ
|Ψ
0
(4.87)
with E
H
0
bei ng the ground state energy in the Hartree approximation. Because
of p = q the operators, c
†
pσ
and c
qσ
can be interchanged with a sign change
and the four-operator expression becomes a product of number operators or
their r espective eigenvalues, the occupation factors n
qσ
,n
pσ
. Thus one finds

4.4 Hartree–Fock Approximation 99
E
HF
0
= E
H
0
−
σ,q,p
q=p
e
2
2ε
0
V |q − p|
2
n
qσ
n
pσ
. (4.88)
Taking E
H
0
from (
4.16) and after summing over σ and considering the
o ccupation factors, gives
E
HF
0
=
3
5
NE
F
−
q,p,q=p
|q|,|p|≤k
F
e
2
ε
0
V |q − p|
2
. (4.89)
The evaluation of the sums is explicitly carried out in the Appendix (
A.5). It
gives
E
exch
= −
3
16π
2
ε
0
Ne
2
k
F
. (4.90)
and leads to the important result of this calculation, the ground state energy
of the electron gas in HF approximation
E
HF
0
=
3
5
N
¯h
2
k
2
F
2m
−
3
16π
2
ε
0
Ne
2
k
F
. (4.91)
Due to the negative contribution of the exchange interaction it is lower than
the result of the Sommerfeld model. In the formulation with the dimensionless
density par ameter r
s
defined in Sect.
4.1 it reads
E
HF
0
= N
+
3
5
9π
4
!
2/3
1
r
2
s
−
3
4π
9π
4
!
1/3
2
r
s
,
Ry. (4.92)
As mean value energy per electron the result is written in the form
ǫ
HF
0
=
1
N
E
HF
0
=
2.2099
r
2
s
−
0.916
r
s
Ry. (4.93)
It is exp ressed in terms of inverse powers of the density parameter r
s
,which
for the same electron density n can have quite different values depending on
the material (see Table 4.1) in which it is realized (Problem 4.6).
In or d er to go beyond the HF approximation (which is a first order per-
turbation calculation) one may consider the second order correction becausse
of the Coulomb interaction. This is formulated in Problem 4.7. As it will turn
out, this term is logarithmically divergent. Thus higher order perturbation
calculation seems not to be the proper way to treat Coulomb interaction and
special many-body techniques are required to improve the result. But we can
take from (
4.93) the message that the HF approximation works well in the
high density limit (r
s
≪ 1).
At this point, two considerations about the HF approximation can be
made. The first one aims at an approximate formulation of H
jell
(
4.85)asan
effective single-particle operator

100 4 The Free Electron Gas
H
jell
≃
kσ
ǫ
HF
kσ
c
†
kσ
c
kσ
(4.94)
with single-particle energi es ǫ
HF
kσ
, which besides the kinetic energy of free par-
ticles contain a contribution from the Coulomb interaction according to the
HF approximation. A systematic way to calculate ǫ
HF
kσ
is the formulation of
the equation of motion for the time-dependent fermion operator
d
dt
c
†
kσ
=
1
i¯h
/
H
jell
,c
†
kσ
0
. (4.95)
The commutator of c
kσ
with the interaction term generates terms consisting
of three fermion op erators. Here the HF approximation means to replace these
terms by the product of an expectation value of the number operator and the
remaining fermion operator. This classifies the HF approximation as a mean
field approximation, see Sect.
6.5. The result takes the form
d
dt
c
†
kσ
=
1
i¯h
ǫ
HF
kσ
c
†
kσ
(4.96)
with the single-particle energy
ǫ
HF
kσ
=
¯h
2
k
2
2m
−
e
2
ε
0
V
q=k
|q|≤k
F
1
|q − k|
2
. (4.97)
The evaluation of the sum over q in the Fermi sphere can be performed as an
integral in polar coordinates with ϑ being the angle between q and k
qk
|q|≤k
F
1
|q − k|
2
=
V
(2π)
3
2π
k
F
0
dqq
2
+1
−1
dcosϑ
q
2
+ k
2
− 2kq cos ϑ
=
V
(2π)
2
k
F
0
dq
q
2k
ln
(q − k)
2
(q + k)
2
. (4.98)
The last integral can be found in an integral table. Finally, we obtain for the
single-particle energy in HF approximation
ǫ
HF
kσ
=
¯h
2
k
2
2m
−
e
2
k
F
4π
2
ε
0
1+
k
2
F
− k
2
2kk
F
ln
"
"
"
k
F
+ k
k
F
− k
"
"
"
!
. (4.99)
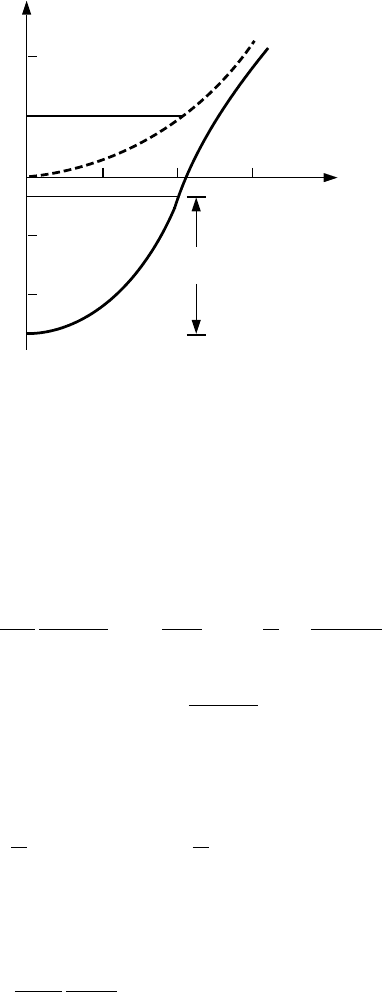
Aplotofǫ
HF
kσ
is shown in Fig. 4.12 for a particular choice of the electron density
n in reduced units together with the free electron dispersion.
As for the ground state energy, we find for the single-particle energies in the
HF approximation a lowering with respect to the free particle energy. Taking
the sum over these single particle energies in the Fermi sphere leads back to
the result of (
4.93). Replacing the Hamiltonian of the jellium model (4.85)as
indicatedin(
4.94) corresponds to describing the interacting free electrons as
4.4 Hartree–Fock Approximation 101
Band width
0.5
1
1.5
(k/k
F
)
2
1
0
–1
–2
ε/ε°
F
Fig. 4.12. Single-particle HF energy (solid line)forr
s
= 4 in comparison with free
particle energy (dashed line), after [
12]
noninteracting quasi-particles, whose single-particle energies incorporate part
of the Coulomb interaction. This quasi-particle con cept is frequently used in
many-body theory.
The second consideration concerns the charge density connected with
the exchange interaction. For this purpose, we may rewrite the exchange
correction with the Fourier transform of the Coulomb interaction as
−
q=k
|q|≤k
F
e
2
ε
0
V
1
|q − k|
2
= −
e
2
4πε
0
q=k
|q|≤k
F
1
V
e
i(q−k)·r
r
d
3
r
= −
eρ
HF
k
(r)
4πε
0
r
d
3
r. (4.100)
The last expression corresponds to the potential energy of an electron at r =0
in a charge density ρ
HF
k
(r) (the HF or exchange charge density) resulting from
all electrons in the Fermi sphere having the same spin:
ρ
HF
k
(r)=
e
V
q=k
|q|≤k
F
e
i(q−k)·r
=
e
V
e
−ik·r
q=k
|q|≤k
F
e
iq·r
. (4.101)
By performing the sum over q as integral over the Fermi sphere in polar
coordinates one obtains
ρ
HF
k
(r)=
2e
(2π)
2
e
−ik·r
r
3
(sin (k
F
r) − k
F
r cos (k
F
r)) . (4.102)
The mean value of ρ
HF
k
(r) over the Fermi sphere gives the averaged HF charge
density
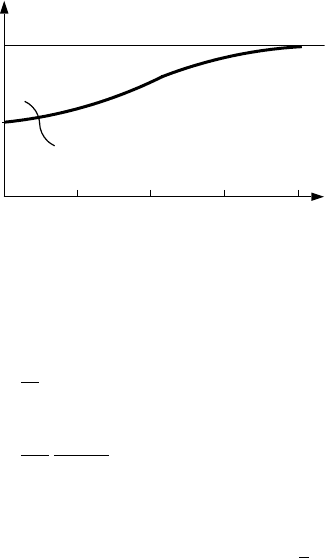
102 4 The Free Electron Gas
g(r)
1
1/2
01234
Fermi or exchange hole
k
F
r
Fig. 4.13. Pair–distribution function g(r)=1−ρ
HF
(r)/en showing the depression
in the vicinity of r = 0 known as Fermi or exchange hole
ρ
HF
(r)=
2
N
k
|k|≤k
F
ρ
HF
k
(r)
=
9N
2V
e
(k
F
r)
6
(sin(k
F
r) − k
F
r cos(k
F
r))
2
. (4.103)
The limits
ρ
HF
(r →∞)=0 and ρ
HF
(r → 0) =
1
2
en (4.104)
indicate the modification of the constant charge density −en of the nonin-
teracting electron gas due to the exchange correction. In the vicinity of an
electron with given spin, the charge density is reduced by 50% correspo n din g
to the interaction with all electrons having the same spin. With increasing
r, the density approaches the value of the nonintera cting electron system.
This r esult can be expressed in terms of the pair–distribution function (see
Sect.
1.3)
g(r)=1−ρ
HF
(r)/en (4.105)
for free electrons in the HF approximation, which is depicted in Fig. 4.13.
It shows a depression around r =0whichistheFermi or exchange hole
and visualizes the correlation due to the exchange interaction or the Pauli
principle.
4.5 The Dielectric Function
The dielectric function is the response of the system (here the homogeneous
electron system) to a perturbation by an electromagnetic field. It is conve-
nient to consider this perturbation as having the characteristic space and

4.5 The Dielectric Function 103
time dependence given by exp(i(q · r − ωt)) typical for a Fourier component
with q and ω. One can distinguish this perturbation caused by a moving
charge (as in a particle scattering process) from that of an electromagnetic
wave. The latter case, leading to the transverse dielectric function has been
the subject of Sect.
3.5. Here we consider the former case: T h e moving charge
is connected with a longitudinal field (directed parallel to the momentum of
the moving particle) and the response is the longitudinal dielectric function
ε(q,ω). For ω = 0 this case includes also the response of the electron sys-
tem to a static charge placed into the e lectron system: The electrons will
arrange around this static charge due to Coulomb attraction (if the static
charge is positive) or repulsion (if it is negative), thus increasing or reducing
the otherwise homogeneous density. This effect is known as static screening.
In Sect.
2.5, the inverse dielectric function has been introduced already in
an exact formulation for an arbitrary system as density–density correlation
function between density and number fluctuations. Here we want to derive the
inverse dielectric function for the homogeneous electron gas. Starting point is
the electron system described by H
jell
and the external perturbation by V
ext
H = H
jell
+ V
ext
. (4.106)
Having in mind the results of Sect.
2.5, it is advantageous to use the for-
mulation of H
jell
in terms of number fluctuations
ˆ
N
k
=
pσ
c
†
p+kσ
c
pσ
(see
Problem 4.8)
H
jell
=
kσ
¯h
2
k
2
2m
c
†
kσ
c
kσ
+
1
2
k=0
v
k
ˆ
N
†
k
ˆ
N
k
− N
(4.107)
and write the perturbation as
V
ext
= −v
q
N
ext
e
iq·r−iωt
= −v
q
ˆ
N
−q
N
ext
e
−iωt
(4.108)
where we have replaced exp(iq · r)by
ˆ
N
−q
.
The response of the homogeneous electron system to a perturbation by an
external charge will be a deviation from the homogeneous density in terms
of numb er (or density) fluctuations. For V
ext
as given in (
4.108) the induced
number fluctuations are described by
N(r,t)=
ˆ
N
q
e
iq·r−iωt
. (4.109)
In the context of Poisson’s equation, the external test charge eN
ext
and
the induced charge (density) fluctuation eN (r,t) play the role of free and
polarization charges, respectively, or in other words: eN
ext
/V is the source of
the dielectric displacement field D while both eN
ext
and eN (r ,t) determine
the electric field E, both fields being connected by the dielectric function:
D(q,ω)=ε
0
ε(q,ω)E(q,ω). Thus, as in Sect. 2.5 we may write

104 4 The Free Electron Gas
iq · E(q,ω)=
e
Vε
0
N
ext
+
ˆ
N
q
(4.110)
iq · D(q,ω)=
e
V
N
ext
(4.111)
and obtain from these equations the relation
1
ε(q,ω)
=1+
ˆ
N
q
N
ext
. (4.112)
From (
4.108)and(4.109)weidentify
ˆ
N
−q
and
ˆ
N
q
as the operators
ˆ
B and
ˆ
A,
respectively, of the response formalism, to write the exact expression for the
inverse longitudinal dielectric constant as (see (
2.80))
1
ε(q,ω)
= 1 + lim
Γ →0
v
q
i
¯h
∞
0
dτe
iωτ−Γτ
[
ˆ
N
q
(τ),
ˆ
N
−q
(0)]
0
(4.113)
where the damping factor regularizes the integral.
The thermal expectation value under the integral is to be evaluated with
the eigenstates of the Hamiltonian H
jell
of the unperturbed system. As these
are not known, this can be done only approximately. For T =0Kthethermal
expectation value reduces to the expectation value of the ground state |Ψ
0
(see Problem 2.2) and we may write
Ψ
0
|[
ˆ
N
q
(τ),
ˆ
N
−q
(0)]|Ψ
0
=
m
&
Ψ
0
|
ˆ
N
q
(τ)|Ψ
m
Ψ
m
|
ˆ
N
−q
(0)|Ψ
0
−Ψ
0
|
ˆ
N
−q
(0)|Ψ
m
Ψ
m
|
ˆ
N
q
(τ)|Ψ
0
'
. (4.114)
The matrix elements can b e evaluated by making use of
ˆ
N
q
(τ)=e
i
¯h
H
jell
τ
ˆ
N
q
e
−
i
¯h
H
jell
τ
and
ˆ
N
−q
=
ˆ
N
†
q
(4.115)
to yield ¯hω
m0
= E
m
− E
0
Ψ
0
|[
ˆ
N
q
(τ),
ˆ
N
−q
(0)]|Ψ
0
=
m
|Ψ
0
|
ˆ
N
q
|Ψ
m
|
2
(
e
−iω
m0
τ
− e
iω
m0
τ
)
. (4.116)
Thus we obtain the exact expression for the longitudinal dielectric function
at T =0K
1
ε(q,ω)
= 1 + lim
Γ →0
v
q
¯h
m
|Ψ
0
|
ˆ
N
q
|Ψ
m
|
2
1
ω
m0
+ ω +iΓ
+
1
ω
m0
− ω − iΓ
. (4.117)
Formally, this result is the same as for χ(ω) derived in Sect.
3.5 for a trans-
verse perturbation, where however the matrix elements are those of the dipole
operator while here they are those of the operator of numb er fluctuations.
