R?ssler U. Solid State Theory: An Introduction

Подождите немного. Документ загружается.

The Free Electron Gas

The structure of a solid, its composition of atoms, as well as the electronic,

optical, and lattice properties are essentially determined by the electrons.

However, not all electrons of the atoms constituting the solid are involved in

the same way. At the beginning of Chap.

2 we have distinguished between the

core electrons and the valence electrons. The former are tightly bound to the

nuclei and extend over a distance (much) smaller than the lattice constant,

while the wave functions of the latter overlap with those of the neighboring

atoms, thus giving rise to the chemical binding. Therefore, we describe the

solid as being composed o f ions (nuclei plus closed shell electrons) in equi-

librium positions at R

and valence electrons, which are responsible for the

stability of the solid and its electronic properties. They are ruled by the Hamil-

tonian (see discussion of (

2.12))

H =



l=1



k,l=1

k=l

4πε

− r



n,l

v(r

− R



V (R

− R

), (4.1)

where N denotes the number of electrons. The ﬁrst a nd second term describe

the kinetic energy of the electrons and the electron–electron interaction,

respectively. The third term, the interaction between valence electrons and

ions, and the fourth term, the ion–ion interaction, depend on the equilibrium

positions R

of the ions (for simplicity a Bravais lattice is assumed) and are

responsible for the structural aspects. The structure of the solid is deﬁned by

the conﬁguration {R

, all n} with the lowest eigenvalue of H.Thisoperator

comprises all terms of the Hamiltonian of the solid (

2.12), if the ions are ﬁxed

at their equilibrium positions. It has to be augmented by spin-dependent terms

if related eﬀects (e.g., spin-orbit coupling, Zeeman eﬀect) shall be considered

(see Sects.

4.2, 4.3,andChap.5).

U. R¨ossler, Solid State Theory,

DOI 10.1007/978-3-540-92762-4

 Springer-Verlag Berlin Heidelberg 2009

76 4 The Free Electron Gas

Instead of this complex problem, for which only approximate solutions

can be found with numerical methods, we want to consider in this chapter the

much simpler problem of the homogeneous electron gas. It is characterized by

neglecting the structural aspects and by replacing the conﬁguration of point-

like p ositive ions by a homogeneous p ositive background charge to ensure

charge neutrality of the system (Problem 4.1). This so-called jellium model

(remember the diﬀerence between jelly and conﬁture) represents a many-body

system of free charged fermions, which – replacing the Coulomb interaction

by a more general two-particle interaction – applies also to physical systems

beyond solid state physics. Thus, the treatment of the homogeneous electron

gas, the calculation of its ground state energy per particle (which in diﬀerent

approximations can be done even a n alytically) becomes an introdu ction to

the concepts of many-b ody theory, which have their bearings also in nuclear

or astrophysics.

4.1 Free Electrons Without Interaction

In order to have a simple ﬁrst look at the homogeneous electron gas, we

want to neglect for the moment the interaction between the electrons (the

second term in (

4.1)) and the interaction with the positive background charge

(corresponding to the third term in (

4.1)) together with the fourth term, the

electrostatic interaction energy of the ion conﬁguration. This simpliﬁcation

is reasonable because in the jellium model these terms compensate exactly if

one also considers the electrons as b eing smeared out just as the positive ions

(see Problem 4.1). Thus instead of the Hamiltonian H of (

4.1)weconsider



l=1

, where H

, (4.2)

with the Schroedinger equation

Ψ({r

})=E Ψ({r

}), (4.3)

where Ψ depends on the conﬁguration {r

} = {r

,...r

} of the N electrons.

With H

being a sum of single-pa rticle operato rs, this N-particle problem

can be separated by assuming Ψ({r

}) to be a product of single-particle wave

functions

Ψ({r

})=

l=1

). (4.4)

We employ Ritz’ variational principle

Ψ|H

|Ψ−



(ψ

|ψ

−1)

=0 (4.5)

4.1 Free Electrons Without Interaction 77

to minimize the exp ectation value of H

under the constraint of normal-

ized single-particle wave functions ψ

). The contraint is w eighted with

the Lagrangian parameter ǫ

.Using(

4.2)and(4.4)weformulate(4.5)as

variational derivative with respect to ψ

∗

′

δψ

∗

′



(ψ

− ǫ

|ψ

 + ǫ

)

=0 (4.6)

to obtain the single-particle problem

)=ǫ

) , (4.7)

which is the same for all electrons. Note, that the Lagrangian parameter ǫ

takes the role of the single-particle energy. The total energy of the N-electron

system can be represented as the sum of the energies ǫ

E =



l=1

(4.8)

of the occupied single-particle states.

The sin gle-particle problem (

4.7)withH

from (

4.2)isthatofafree

particle and has the solution

(r)=

√

ik·r

(4.9)

with the eigenvalues

ǫ(k)=

¯h

. (4.10)

The single-particle wave function is normalized to the ﬁctitious (or crystal)

volume V , which encloses the considered N electrons (particle in the box). Let

V be a cuboid with side lengths L

,i=1, 2, 3 and assume periodic boundary

conditions (see problem 3.3), according to which ψ

(r) is periodic with the

. These conditions r estrict the components of k to the discrete values (see

(

3.18))

2π

integer,i=1, 2, 3 (4.11)

as shown in Fig.

4.1. The periodic boundary conditions are a trick to obtain

discrete states, which can be counted. It should be clear, however, that the

relevant physical quantity, on which all observables of the system depend, is

the single-particle density n = N/V (and not the particle number N). It is

kept constant for V →∞.

The wave vector k (or else the triple n

of (

4.11)) characterizes the

single-particle state except for the spin degree of freedom. Each of the (quasi-

discrete) k takes a volume (2π)

/V . The state with lowest energy at T =0K

78 4 The Free Electron Gas

2π

Fig. 4.1. (k

) plane with discrete k values due to the periodic boundary con-

ditions. In the ground state at T = 0 K all points up to the radius k

, deﬁning the

Fermi sphere, are occupied

for N electrons in the volume V ,theground state, is o btained by occupying

the single-particle states with lowest possible ener gy wit h the constraint of

Pauli’s principle

which allows two electrons with opposite spin at each k.

This is known as the ideal Fermi gas or Sommerfeld

model [109]. To evaluate

the ground state energy we ﬁrst make use of the energy disp ersion (

4.10),

which is isotropic in k, to ﬁnd the number of states in a spherical shell with

radius k and thickness dk:

D(k)dk =

(2π)

4πk

dk. (4.12)

The factor 2 is due to the spin degeneracy. The ground state is deﬁned by

ﬁlling concentric spherical shells around k = 0 with increa sing radius k until

the stock of N electrons is exhausted:

N =



D(k)dk =



dk =

3π

. (4.13)

Here k

denotes the radius of the sphere in k space, the Fermi sphere,within

which at T = 0 K all states are occupied (Fig.

4.1). This radius is determined

by the density n = N/V of the homogeneous electron gas:

=(3π

1/3

, radius of the Fermi sphere . (4.14)

Wolfgang Pauli 1900–1958, Nobel prize in physics 1945

Arnold Sommerfeld 1868–1951

4.1 Free Electrons Without Interaction 79

Particles with k

have the energy

¯h

, Fermi energy (4.15)

which separates the occupied states from the empty ones. The ground state

energy of the system containing N electrons fo llows to be



¯h

D(k)dk =

(4.16)

which, when divided by N, gives the average energy per particle in the ground

state

. (4.17)

With (

4.15)and(4.14), one obtains the relation between ǫ

and the particle

density n

¯h

(3π

2/3

. (4.18)

Frequently, a dimensionless density parameter r

is used. In the proper

unit of length (Bohr’s radius a

=4πε

¯h

/me

) it deﬁnes for a given density

the radius of the Wigner–Seitz sphere whose volume can b e allocated to each

particle, V/N =1/n =4π(r

)

/3. One ﬁnds easily

9π

1/3

(4.19)

and (in the unit 1 Ry = me

/2(4πε

¯h)

of energy)

9π

2/3

Ry =

2.2099

Ry. (4.20)

Corresponding to this relation, the mean energy per particle increases with

increasing density to the extent by which states with larger k are occupied

under the constraint of Pauli’s principle. Chara cteristic quantities related

to k

or E

are the Fermi velocity v

=¯hk

/m,theFermiwavelength

=2π/k

,andtheFermi temperature T

= E

,wherek

is the

Boltzmann constant.

Supplement: Parameters of fermion systems

The concepts developed so far allow one to distinguish fermion systems by their

diﬀerent particle densities n (or r

) and the derived quantities. They are given for a

selection of solid state fermion systems in Table 4.1. Potassium (K) has one v alence

electron and crystallizes in the body centered cubic lattice with t wo atoms and thus

two electrons in the elementary cube. Copper (Cu), also with one valence electron

80 4 The Free Electron Gas

Table 4.1. Parameters (n in cm

−3

, k

−1

, v

in 10

cm s

−1

, E

in eV, T

K) for diﬀerent fermion systems realized in solids

System nr

K1.43 · 10

4.83 0.75 0.87 2.14 2.48

Cu 8.53 · 10

2.66 1.36 1.57 7.05 8.18

n-GaAs 10

1.29 0.014 0.25 0.75·10

−3

0.0009

n-GaAs 10

0.129 0.143 2.5 0.078 0.09

p er atom, forms a face centered cubic lattice with four atoms and consequently

four electrons in the elementary cube. Given the lattice constants a

=5.31

Aand

=3.61

A one easily obtains the electron density n and the other system param-

eters depending on n. The values given in Table 4.1 for K and Cu are characteristic

for normal and noble metals, respectively. For comparison we also quote numbers

for n-GaAs with two diﬀerent doping concentrations.

In evaluating the electron density of the metals, we have only considered the

valence electrons outside of closed shells. Similarly, in doped semiconductors we

count only the extra electrons provided by electron donating impurity atoms (e.g.,

Si substituting Ga in GaAs) to d etermine n. The properties of these extra electrons

deviate, however, from those of free electrons in vacuum. Their energy–momentum

relation is modiﬁed by the periodic crystal potential and becomes a band structure

(see Chap.

5), in which t hese extra electrons occupy states at the bottom of the

conduction band with a disp ersion similar to free particles but with an eﬀective

mass m

∗

diﬀerent from the free electron mass m; their charge is screened with

the (relative) dielectric constant ε. Correspondingly, the system Hamiltonian would

contain these modiﬁed electron parameters in the kinetic energy and in the electron–

electron interaction. Therefore, the atomic units are redeﬁned as eﬀective units a

∗

(εm/m

∗

and 1 Ry

∗

=(m

∗

/mε

)Ry. In these units, one obtains for the two doping

concentrations in n-GaAs with m

∗

/m =0.066 and ε =12.9 the corresponding

parameter values given in Table 4.1 . In spite of their much lower particle density

the doped semiconductors appear as interacting fermion systems with much higher

density (smaller r

) than the metals. This is due to the much larger eﬀective Bohr

radius, which is the length scale for the interaction.

Fermion systems with quite diﬀerent densities are realized in neutron stars and

systems of atoms conﬁned in electromagnetic traps. Neutron stars have a radius of

about 10 km and evolve from the gravitational collapse of small stars with about the

mass of the sun. They can be described as an ideal Fermi gas with the extremely

high density of 10

−3

! The other extreme of very low densities is obtained by

cooling ensembles of fermionic atoms conﬁned in electromagnetic traps to extremely

low temperatures (T

< 1μ K), at which they represent degenerate Fermi systems

(see Physics Today, October 2003, p. 18).

Knowing the single-particle energy-momentum relation ǫ(k)of(

4.10), one

can derive the spectral distribution of the electrons using (

4.12):

D(E)dE = D(k)

dE =

¯h

√

EdE. (4.21)

4.1 Free Electrons Without Interaction 81

The number of states with energy E, the electron density of states,givenby

D(E)=

2π

¯h

3/2

√

E (4.22)

is the well-known square root rela tion shown in Fig.

4.2. Alternatively, one can

calculate the density of states also from D(E)=2



δ(E − ǫ(k)) (see for

comparison the phonon density of states (

3.53)), by collecting in k space all

single-particle energies with ǫ(k)=E. The factor 2 takes into account the

spin degeneracy.

At T = 0 K, all states with energy smaller than E

are occupied and the

ground state energy E

for N particles is obtained by integrating ED(E)up

to the Fermi energy E

. More generally, to include ﬁnite temperatures the

ground state energy follows from

(T )=

∞



ED(E)f(E, μ,T)dE (4.23)

D(E) 3D

E = µ(T=0)

µ(T>0)

D(E)

T=0

T>0

µ(T)=E

Fig. 4.2. Density of states of free electrons in three (upper part)andtwo(lower part)

dimensions. At T =0KallstateswithE ≤ E

are occupied. For ﬁnite temperatures

the occupation around the Fermi energy is smeared out and is determined by the

chemical potential μ(T )

82 4 The Free Electron Gas

with the Fermi–Dirac distribution function

f(E,μ,T)=

(E−µ)/k

. (4.24)

Here the chemical potential μ is ﬁxed (similar to k

in (

4.13)) by the particle

density n = N/V :

∞



D(E)f(E,μ,T)dE. (4.25)

Due to the interplay between density of states and distribution function the

chemical po tential depends in general on T (Problem 4.2). However, for a

two-dimensional electron system with constant density of states (as depicted

in the lower part of Fig.

4.2) this is not the case (provided the Fermi energy is

suﬃciently high up in the band). At T =0K,f(E,μ,T) degenerates to a step

function with a step at E

and one identiﬁes μ(T → 0) → E

(see Fig.

4.2).

But for ﬁnite T i n general, quantities such as the ground state energy or the

particle density, which require to integrate some power function in E with

the Fer mi–Dirac distribution function, can be expressed in terms of Fermi

integrals (see Appendix).

Taking the T dependent chemical po tential from Problem 4.2 (which

applies for T → 0),thethermalenergydensity of free electrons at ﬁxed

volume is found (Sommerfeld expansion, see Appendix)

ǫ(T )=ǫ

T )

D(E

)+... (4.26)

with ǫ

from (

4.20). Its derivative with respect to T is the electron contribu-

tion to the speciﬁc heat (at constant V )

(T )=

∂ǫ(T )

∂T

TD(E

. (4.27)

This linear dependence on T is characteristic for metals and can be detected

experimentally at low temperatures. Taking into account the simultaneously

present lattice contribution also(see Chap.

3), we write c

(T )=γT + AT

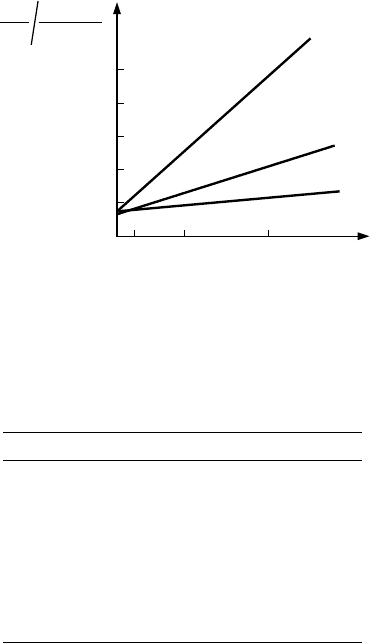
and ﬁnd in a plot of c

(T )/T versus T

the Sommerfeld coeﬃcient γ (see

Fig.

4.3).

Sommerfeld parameters obta ined from experimental data of the speciﬁc

heat (γ

exp

) can be compared with those from the Sommerfeld model (γ

)

calculated with the respective particle density (see Table 4 . 2). The compari-

son can be quantiﬁed by realizing that accor ding to (

4.27) the speciﬁc heat

is proportional to the density of states at the Fermi energy and thus to the

particle mass. Thus the ratio of the Sommerfeld parameters corresponds to

the ratio of the fermion mass obtained from the measured speciﬁc heat (m

)

to the free electron mass m. In Table 4.2 we ﬁnd good agreement between the

4.1 Free Electrons Without Interaction 83

1 4 9 (T/K)

mol K

Fig. 4.3. Measured values of c

/T for Au, Ag, Cu vs. temperature. The

extrapolated value for T = 0 K gives the Sommerfeld coeﬃcient γ

exp

Table 4.2. Sommerfeld coeﬃcients from the free electron model (γ

)andfrom

experiment (γ

exp

)(inmJMolK

−2

) and the corresponding mass ratio [

29]

System γ

exp

Na 1.38 1.094 1.26

K 2.08 1.668 1.25

Al 1.35 0.912 1.48

Cu 0.695 0.505 1.38

Ag 0.646 0.645 1.00

Au 0.729 0.642 1.14

Fe 4.98 0.498 10.0

Ni 7.02 0.459 15.3

Sommerfeld model and the experimental data, i.e., m

/m ≃ 1, for the alkali

and no ble metals, whose valence shells contain s and p electrons. However,

even dramatic deviations, m

/m ≫ 1, are observed for transition metals and

rare earth compounds. As an example, the mass ratio of about 15 for Ni is

given in Table 4.2. It can be ascribed to the inﬂ uence of the periodic potential

(Chap.

5) and understood as a single-particle or band structure eﬀect. How-

ever, mass ratios of the order of 10

found for the rare earth compounds are

in addition due to electron–electron interaction or electronic correlation (see

Sect. 7.5). The latter materials are called heavy fermion systems [

110].

In this section, we have assumed a three-dimensional electron system in

deriving e.g., the density of states in (

4.12)and(4.22) and the parameters of

the Fermi sphere. But electron systems of lower dimension (d =2,1,and0)

can also be realized at semiconductor hetero-interfaces, by using modern

device technologies to produce quantum wires or dots, or in molecular systems

like carbon nanotubes [

21, 111–114]. These low-dimensional electron systems

exhibit characteristic phenomena which can be understood in parts from the

84 4 The Free Electron Gas

dimension-speciﬁc density of states (see e.g., Fig.

4.2 for the two-dimensional

case and Problem 4.3).

4.2 Free Electrons in a Magnetic Field

The orbital motion of electrons and their energy spectrum change in a homo-

geneous magnetic ﬁeld. At the same time, the magnetic ﬁeld acts on the

electron spin. Both eﬀects result in some o f the magnetic properties of the

electron system. For their description the single-particle Hamiltonia n H

(

4.2) is to be replaced by

H =

(p + eA)

e¯h

σ · B . (4.28)

Here we denote the magnetic induction B = μ

H, connected with the external

homogeneous ﬁeld by the vacuum permeability μ

, as magnetic ﬁeld. If its

direction is along z, B =(0, 0,B), it can be described in the Landau gauge

by the vector potential A =(0,Bx,0). In a classical description, the ﬁrst term

in (

4.28) leads to the circular motion as a consequence of the Lorentz force.

It represents a harmonic oscillator with the cyclotron frequency ω

= eB/m,

which in the quantum mechanical treatment gives the characteristic oscillator

spectrum. The second term, containing the vector σ of the Pauli spin matrices,

is the Zeeman

term resp onsible for the removal of the spin degeneracy by the

magnetic ﬁeld.

Let us calculate ﬁrst the eigenvalues of H by considering the commutation

relations for the components of the vector operator π = p + eA:

[π

,π

]=e(p

− A

)=−i¯heB, [π

,π

]=[π

,π

]=0. (4.29)

They can be written in the compact form of a vector relation

π × π = −ie¯hB . (4.30)

Because of the translational invariance of H in the z-direction (parallel to the

magnetic ﬁeld) we have [p

,H] = 0 , and the linear momentum p

=¯hk

is a

constant of motion. The Hamiltonian

H =

(π

+ π

¯h

+ μ

B (4.31)

(with the Bohr magneton μ

= e¯h/2m) can now be rewritten by making use

of oscillator operators a, a

†

according to

Lev Davido vich Landau 1908–1968, Nobel prize in physics 1962

Pieter Zeeman 1865–1943, Nobel prize in physics 1902