R?ssler U. Solid State Theory: An Introduction
Подождите немного. Документ загружается.

290 9 Defects, Disorder, and Localization
and we identify the dimensionless conductance g(L)=σL
d−2
,wherethe
conductivity σ characterizes the material property and does not depend on L.
Using this relation, the scaling argument (
9.96) can be discussed with respect
to its dependence on the system dimension d (see Problem 9.5). As it turns out,
the universal function β(g) passes through zero only for a three-dimensional
system. For a two -dimensional system, it approaches zero asymptotically for
large g and is always negative for d = 1. This means tha t a disorder-driven
metal–insulator transitio n should be possible only for d>2. Detailed investi-
gations of two-dimensional electron systems seem to disprove this conclusion
[
278]. The critical discussion in the light of these data leads to the result,
that possibly disorder is not the only mechanism but that electron–electron
interaction may contribute, which is not in clud ed in the scaling theory.
Problems
9.1 Verify the eigenvalue equation (
9.27) for the additional poles of the full
Green function G(E)(
9.20) by making use of the block-diagonal form of
the short-range defect matrix.
9.2 To demonstrate self-averaging, consider the classical resistance R =
N
i=1
r
i
of N resistances r
i
,i =1...N in a row. Make sure that the
average r exists and that R = Nr. Calculate the relative variance of
R and show that it tends to zero with increasing N or system size!
9.3 Calculate the current–current response χ(0,ω)of(
9.83) with the current
operator
ˆ
j
p
of (
9.86) to obtain the conductivity σ(0,ω)(9.88).
9.4 Show that the double sum expression under the integral of σ
dc
(
9.89)can
be cast into the form Tr(ˆvImG(E
+
)ˆvImG(E
+
)).
9.5 Discuss the asymptotics of β(g)forg →∞(using σ independent of L)
and for g → 0 (assuming g(L) ∼ exp (−L/λ)) in dependence on the sys-
tem dimension d. Show that β(g) < 0 for all g and d ≤ 2 while it changes
sign for d>2.

10
Light–Matter Interaction
The investigation of condensed matter systems using light as a probe is a ver-
satile and powerfull concept, which provides various kinds of information not
only about the structure but also of the electronic and lattice excitations and
their dynamics. Besides linear optical processes, li ke absorption and emission
(including photoemission), light-scattering, two- (or three-)photon absorption,
photo-luminescence and high-excitation spectroscopy also belong to the meth-
o ds to gain information about the single-particle and collective excitations of a
solid. In s emiconductor samples with a proper desig n , coherent light emission
is possible and used in solid-state lasers. These methods, w hi ch allow studies
in the frequency or time domain, are all based on the interaction of light with
matter. In Sect.
3.5 we have already treated the optical excitation of lattice
vibrations as an example. In this chapter, we shall present a systematic the-
oretical description of light–matter interaction, which can b e found in one or
the other representation in standard textbooks[
7, 14, 89, 95, 282, 283].
10.1 Preliminaries
Let us start with the microscopic Maxwell equations
1
∇·E =
ρ
ε
0
, ∇×E = −
∂B
∂t
∇·B =0, ∇×B = μ
0
j +
1
c
2
∂E
∂t
. (10.1)
Here, E(r,t)andB(r,t) are the space and time dependent electric field and
magnetic induction, respectively. The latter can be replaced with B = μ
0
H
by the magnetic field H(r,t). ε
0
and μ
0
are the vacuum constants and
c =1/
√
ε
0
μ
0
is the vacuum velocity of light. In this microscopic formula-
tion, ρ(r,t)andj(r ,t) are the charge and current densities, respectively, of
1
James Clark Maxwell 1831–1879.
U. R¨ossler, Solid State Theory,
DOI 10.1007/978-3-540-92762-4
10,
c
Springer-Verlag Berlin Heidelberg 2009

292 10 Light–Matter Interaction
all charged particles in the system (nuclei and electrons). We could adopt
here the rea sonable concept of the previous chapters, according to which we
understand the solid as composed of ions and valence electrons. In this case
ρ(r,t)andj(r,t) would be connected with the latter, while the electrons in
closed shells would belong to the ions, which essentially do not contribute to
the material pr operties of the solid. We come back to this point later in this
Chapter.
For what follows, instead of the fields E(r,t)andB(r,t), it is convenient
to introduce the potentials A(r,t)andφ(r,t), which are related to the fields
by
B = ∇×A , E = −∇φ −
∂A
∂t
. (10.2)
Replacing E and B in Maxwell’s equations by the potentials A and φ,we
may write (using ∇×∇×A = ∇(∇·A) −∆A) the inhomogeneous equations
in the form
∆A −
1
c
2
∂
2
A
∂t
2
−∇
∇·A +
1
c
2
∂φ
∂t
!
= −μ
0
j (10.3)
and
∆φ +
∂
∂t
(∇·A)=−
ρ
ε
0
. (10.4)
The potentials are free to a gauge transformation with the scalar gauge field
χ(r,t)
A → A + ∇χ, φ → φ −
∂χ
∂t
, (10.5)
which leaves (
10.2), i.e., the fields E and B, invariant.
Among the commonly used gauges, the transverse or Coulomb gauge, ∇·
A = 0, is the appropriate one for the interaction of light with matter in the
form of solids. With this choice, the third term on the lhs of (
10.3)vanishes
while (
10.4) becomes Poisson’s equation. Thus, we obt ain the potential form
of Maxwell’s equations in the form of an inhomogeneous wave equation for
the vector potential
∆A −
1
c
2
∂
2
A
∂t
2
= −μ
0
j. (10.6)
The inhomogeneity is connected with the nuclei and electrons (or ions and
valence electrons) and vanishes outside the solid, where (
10.6) describes the
free propagation of electro-magnetic waves in vacuum.
Consider now the solid interacting with the electro-magnetic field of the
light. In the most general case, it is described by the Schroedinger equation
with the Hamiltonian of the solid (
2.1), including the electro-magnetic field.
After having dealt already with the excitation of optical phonons, which are
connected with the moving ions (see Chap.
3.), we would like to consider here
only the electrons as movable charged particles in a rigid periodic arrangement
10.1 Preliminaries 293
of nuclei or ions. Thus, we restrict in this chapter to the interaction of light
with the electrons of the solid and start accordingly with the Hamiltonian
(
5.2) for the electrons. To include the electro-magnetic field, we have to take
into account its energy and to fulfill the requirement, that the time-dependent
Schroedinger equation
H
N
Ψ
N
=i¯h
∂Ψ
N
∂t
(10.7)
has to be invariant under the gauge transformation (
10.5), together with a
simultaneous gauge transformation of the time-dependent N-electron wave
function Ψ
N
(r
1
...r
N
,t)
Ψ(r
1
...r
N
,t) → exp
−i
e
¯h
{χ(r
1
,t)+···+ χ(r
N
,t)}
Ψ(r
1
...r
N
,t) .
(10.8)
This is achieved by th e replacement
p
l
→ p
l
+ eA(r
l
,t) . (10.9)
For the rest of this chapter the following Hamiltonian will be the starting
point:
H
N
=
N
l=1
1
2m
(p
l
+ eA(r
l
))
2
+
1
2
k,l=1
k=l
e
2
4πε
0
|r
k
− r
l
|
+
n,l
v(r
l
− R
0
n
)
+
1
2
mn
V (R
0
n
− R
0
m
)+
ε
0
2
d
3
r
E
2
+ c
2
B
2
. (10.10)
In the last term, describing the energy of the radiation field, E and B can b e
replaced with (
10.2) by the vector potential to yield
H
rad
=
ε
0
2
d
3
r
+
∂
∂t
A(r,t)
!
2
+ c
2
(∇×A(r,t))
2
,
. (10.11)
Having in mind linear response theory (Sect.
2.4), we may separate H
N
into
a Hamiltonian for the uncoupled solid and electro-magnetic field, H
0
+ H
rad
,
and an interaction term H
el−rad
for the light–matter coupling
H
N
= H
0
+ H
el−rad
+ H
rad
, (10.12)
where H
0
describes the unperturbed electron system of the solid, (
5.2), and
(by making use of the transverse gauge)
H
el−rad
=
N
l=1
e
m
A(r
l
,t) · p
l
+
e
2
2m
(A(r
l
,t))
2
!
(10.13)

294 10 Light–Matter Interaction
is the time-dependent perturbation by the radiation field, which can be id en-
tified as the external potential of (
2.37). Using j = −e
l
p
l
/m, the first term
can also be written as −j · A (see Sects.
2.4 and 9.4).
10.2 Single-Particle Approximation
In Chap.
5 we have invoked density-functional theory (DFT) to reduce the
many-body problem with H
0
to a single-particle problem, by accounting for
the electron–electron interaction in an effective s i n gle-particle potential V
eff
(r)
(see (
5.30)), which is the same for all electrons. This can now be used to write
the many-body Hamiltonian H
N
as a sum of single-particle terms. Leaving
aside the energy of the radiation field as a constant, the single-particle Hamil-
tonian of an electron interacting with the radiation field takes the form
H = −
¯h
2
2m
∆ + V
eff
(r)+
e
m
A · p +
e
2
2m
A
2
. (10.14)
The eigenstates of the first term are the Bloch states of Chap.
5.Thelasttwo
terms represent a p eriodic time-dependent interaction o f Bloch electrons with
the radiation field. For sufficiently weak amplitudes of the vector potential
they can be treated as perturbations of first an d second order. Sometimes
the Ap -term is also expressed in the form −eE · r,where−er is the dipole
operator (Problem 10.1).
LetusfirsttreatthetermlinearinA. For monochromatic light, its space
and time dependence is given by
A(r,t)=A
0
e e
i(κ·r−ωt)
+ c.c. , (10.15)
with a scalar amplitude A
0
and the unit vector e for transverse polarization,
e ⊥ κ. The frequency follows the linear dispersion relation ω = c|κ| of light
in vacuum.
Because of the periodic time-dependence of the perturbation, Fermi’s
Golden Rule applies and we can immediately write the rate for the transition
probability between Bloch states
W
nk,n
′
k
′
=
2π
¯h
|nk|H
′
|n
′
k
′
|
2
δ (E
n
(k) − E
n
′
(k
′
) − ¯hω) , (10.16)
where H
′
= eA
0
exp(iκ · r)e · p/m is the perturbation without the time-
dependent exponential. Together with the time-dependent pha se factors of the
stationary Bloch functions, it results in the δ-function, which expresses the
energy conservation: the energy quantum ¯hω of the radiation field equals
the energy difference between the Bloch states. Depending on the sign of this
difference, the transition between the Bloch states can be an absorption or
emission process.
10.2 Single-Particle Approximation 295
The transition matrix element can be transformed from an integral over
the crystal volume V
c
nk|H
′
|n
′
k
′
=
V
c
ψ
∗
nk
(r)
e
m
A
0
e
iκ·r
e · p
ψ
n
′
k
′
(r)d
3
r (10.17)
to an integral over a Wigner-Seitz cell by shifting r by lattice vectors R
n
and
extracting the corresponding phase factors from the Bloch functions
nk|H
′
|n
′
k
′
=
WSC
...
n
e
i(κ+k
′
−k)·R
n
d
3
r . (10.18)
Here the dots stand for the integrand of the previous integral. The lattice sum
results in a Kronecker δ
k,k
′
+κ
, which represents the momentum conservation
of the excitation process. The diameter of the Wigner–Seitz cell is about the
lattice constant of a few
˚
A, which is much smaller than the wavelength of the
light corresp onding to the typical excitation energy ¯hω of a few eV . Therefore,
the exponential with κ in the integral is almost constant over the cell and
we may safely replace it by 1. This is the dipole approximation. Finally, the
transition matrix element can be written (see also Problem 10.2)
nk|H
′
|n
′
k
′
=
WSC
u
∗
nk
(r)
e
m
A
0
e · p
u
n
′
k
′
(r)d
3
r δ
k,k
′
=
e
m
A
0
nk|e · p|n
′
kδ
k,k
′
. (10.19)
Thus, one obtains a finite transition probability
W
nk,n
′
k
(ω)=
2π
¯h
e
2
A
2
0
m
2
|nk|e ·p|n
′
k|
2
δ (E
n
(k) − E
n
′
(k) − ¯hω) (10.20)
only for dire ct transitions (or vertical transitions), in which the wave vector
of the Bloch state is not changed.
The absorption of light passing through a solid o f thickness d determines
the damping of the light intensity according to
I(d)=I
0
e
−αd
. (10.21)
On t he other side, the absorption coefficient α(ω) is connected with the real
(n
1
) and imaginary (n
2
) parts of the complex index of refraction accordin g to
α =
2n
1
n
2
c
ω, (10.22)
where 2n
1
n
2
= ε
2
is the imaginary part of the complex dielectric function
ε(ω). Microscopically, α(ω) is determined here by the power loss or the rate
by which energy of the radiation field is converted into excitations between

296 10 Light–Matter Interaction
Bloch states[
14, 89]. Thus,
α(ω)=
2¯h
ε
0
cωA
2
0
W (ω) , where W (ω)=
nn
′
k
W
nk,n
′
k
(ω), (10.23)
and the imaginary part of the dielectric function is given by
ε
2
(ω)=
4πe
2
ε
0
m
2
ω
2
nn
′
k
|nk|e · p|n
′
k|
2
δ (E
n
(k) − E
n
′
(k) − ¯hω) . (10.24)
The real part of ε
1
(ω) can be obtained using the Kramers–Kronig relation
(
2.80) formulated for susceptibilities χ(ω). Con sidering the relation ε(ω)=
1+χ(ω)/ε
0
,wehavetouse
ε
1
(ω)=1+
2
π
∞
0
ω
′
ε
2
(ω
′
)
ω
′
2
− ω
2
dω
′
, (10.25)
leading to
ε
1
(ω)=1+
4e
2
ε
0
m
nn
′
k
f
nn
′
(k)
ω
nn
′
(k)
2
− ω
2
(10.26)
with the oscillator str ength
f
nn
′
(k)=
2 |nk|e · p|n
′
k|
2
m¯hω
nn
′
(k)
(10.27)
for the transition between Bloch states with the energy difference ¯hω
nn
′
(k)=
E
n
(k) − E
n
′
(k).
In cubic solids, the dipole matrix elements do not depend on the polariza-
tion dir ection e and usually their dependence on the wave vector is not very
strong. Thus, we can write
nk|e · p|n
′
k≃P
nn
′
(10.28)
with P
nn
′
independent of k and ε
2
(ω) becomes
ε
2
(ω)=
4π
ε
0
e
mω
2
nn
′
|P
nn
′
|
2
D
nn
′
(¯hω) , (10.29)
with the combined density of states
D
nn
′
(¯hω)=
k
δ (E
n
(k) − E
n
′
(k) − ¯hω) (10.30)
10.2 Single-Particle Approximation 297
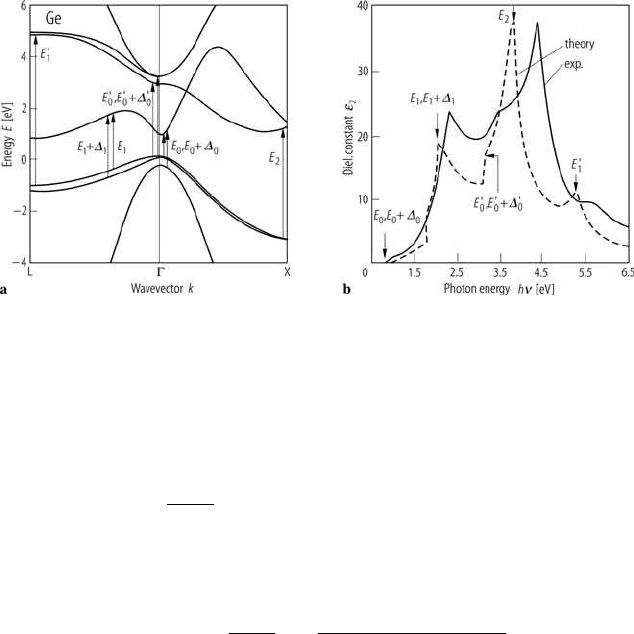
Fig. 10.1. (a) Band structure of Ge with vertical transitions at critical points and
(b) comparison of measured and calculated ε
2
(ω), showing van Hove singularities
at these critical points (from Landolt-B¨ornstein [1])
of the pair of bands n, n
′
. As in Sect.
3.3,thek-sum over the Brillouin zone
can be converted into an integral
D
nn
′
(¯hω)=
V
c
(2π)
3
BZ
δ (E
n
(k) − E
n
′
(k) − ¯hω)d
3
k , (10.31)
which, due to the δ-function, reduces to an integral over the surface S
k
,for
which the energy difference of the Bloch states equa l s ¯hω
D
nn
′
(¯hω)=
V
c
(2π)
3
S
k
dS
k
|∇
k
(E
n
(k) − E
n
(k))|
. (10.32)
The points, at which |∇
k
(E
n
(k) − E
n
(k))| vanishes (critical p oints), give rise
to van Hove singularities in the combined density of states, by which they can
be identified.
As an example, we show in Fig.
10.1 the band structure of Ge in the funda-
mental band gap region with marked direct transitions at critical p oints and
the measured and calculated imaginary part of the dielectric function, ε
2
(ω).
In spite of discrepancies in the critical point energies, there is a clear corre-
spondence between the experimental and theoretical curves. It turns out, that
the optical spectra of semiconducto rs with tetrahedral coordination resemble
each other [
89]. Their band structures have the same topology determined by
the common crystal structure but differ with respect to their critical point
energies E
0
,E
′
0
,.... Investigations of the op t i cal spectra have p aved the road
to the quantitative understanding of semiconductor band structures.
Light–matter interaction stood at the beginning of quantum mechanics
with Einstein’s explanation of the photo-electric effect, which earned him the
Nobel prize in 1922. It is based on the assumption of a quantized radiation
field. Photoemission can take place if the photon energy suffices to excite an

298 10 Light–Matter Interaction
electron beyond the energy barrier at the surface of the solid so that it can
be detected ou tside the solid as free particle. Einstein found (in accordance
with experimental data for metals) the linear dependence of the maximum
kinetic energy of the emitted electrons on the photon energy, which is ruled
by the ratio ¯h/e. Later, this effect has been exploited by Siegbahn
2
to develop
the concept of photo-electron spectr oscopy (PES). It is based on analyzing not
only the maximum energy but also the energy spectrum of the photo-emitted
electrons.
The minimum energy required to free an electron from a metal, is the
difference between the vacuum level and the Fermi energy, known as the work
function. In a semiconductor, with the Fermi energy somewhere in the gap,
this energy would not be sufficient for photoemission, because the highest
occupied state, in the intrinsic case, is the top of the valence band. Instead
it is the ionization energy that defines the threshold for photoemission. The
photoemissive yield is roughly proportional to the density of the initial states.
PES is applied at different photon energies: ultraviolet light (UPS: ultraviolet
PES) for the investigation of valence electron structures and X-rays (XPS)
for the study of the more tightly bound core electrons[
65, 287]. Note, that
for the latter case one has to treat the core electrons in the same way as the
valence electrons.
The photo-emitted electrons can be also analy zed with respect to their
momentum parallel to the surface, which does not change when the electron
leaves the solid. This is done in angular resolved photoemission (ARPES)
experiments, which give information about the energy bands E
n
(k), as shown
in Fig.
10.2 for Cu as an example. The experimental data points map out all
details of the energy bands, which we already know from Chap.
5.
Further variants of photo-electron spectroscopy are spin-polarized UPS
(SPUPS) and the inverse photoemission, in which an electron of known energy
is injected and the emitted photon is detected. The former method allows to
study the bands of minority and majority spins in ferromagnets (see Fig.
6.1),
and the latter yields information about the unoccupied states above the Fermi
energy.
10.3 Excitons
The basic assumption of the single-particle approximation in Sect.
10.2 is the
same effective single-particle potential V
eff
(r) for electrons in all ban d s. This
assumption is correct for the ground state of the solid, which, for a semicon-
ductor, is characterized by filled valence and empty conduction bands. But
for the excited state an electron in the valence band is missing, because it
is in the conduction band. Intuitively, this is the two-particle problem of an
2
Kai Manne B¨orje Siegbahn 1918–2007, Nobel prize in Physics 1981, together with
N. Bloemb ergen and A.L. Schawlow.

10.3 Excitons 299
wave vector
energy (eV)
Fig. 10.2. Calculated energy bands of Cu and data from angular resolved
photoemission, after [
31]
electron–hole pair, if we consider the remaining N −1 electrons in the valence
band as the hole and the missing contribution to the effective potential as
the attractive Coulomb interaction between the electron in the conduction
band and the hole in the valence band. In effective-mass approximation, the
Hamitonian for the electron-hole pair can be written
H
e−h
= E
g
+
p
e
2m
e
+
p
h
2m
h
−
e
2
κ|r
e
− r
h
|
. (10.33)
Note, that the kinetic e nergy of the hole increases in the downward bent
parabola for the valence band. If we only had the two bands (one valence
and one conduction band) in vacuum, then κ =4πε
0
. However, the correct
description has to include all the other valence and conduction bands and the
possible excitations between these bands, i.e., the two -band model for electron
and hole is embedded in a dielectric with material constant ε and, therefore,
κ =4πε
0
ε, i.e., the Coulomb interaction is screened. We would like to mention
here, that the electron–hole interaction is just the difference of the Hartree
potentials in the excited and ground states, but there should also be exchange
and correlation contributions, which we leave aside for the moment.
In relative and center-of-mass co ordinates, using for p
i
=¯h k
i
,i= e, h,
k
e
= k +
m
e
M
Q , k
h
= k −
m
h
M
Q , (10.34)
