R?ssler U. Solid State Theory: An Introduction

Подождите немного. Документ загружается.

310 10 Light–Matter Interaction

long.

CuCi

UPB

LPB

HRS - data

TPA - data

theory

1510

k (10

–1

)

3.16

3.18

3.20

3.22

h ω

(eV)

Fig. 10.8. Calculated exciton–polariton dispersion of CuCl with experimental data

from two-photon absorption (TPA-data) and hyper-Raman scattering (HRS-data),

after [

283]

LPB

UPB

CuCI

2 K

3.18

3.19

E (eV)

3.20

3.21

3.22

k (x 10

–1

)

/ c

–5

–4

–3

–2

–1

(a)

(b)

Fig. 10.9. Exciton–polariton dispersion of CuCl (left) and measured propaga-

tion velocity of polariton modes in CuCl together with values calculated from the

dispersion curve (right), after [

283]

In contrast to simple absorption experiments with one photon, both methods

allow to map out the dispersion of the polaritons by exploiting diﬀerent con-

ﬁgurations of the small wave vectors of incident and scattered photons. It is

also possible to detect the longitudinal polariton branch.

Fig.

10.9 shows, in the left hand part, the dispersion of the transverse

polariton branches on a larger k scale. On this scale, the dispersion of

the lower polariton branch (LPB), caused by the free center-of-mass term in

the exciton energy, becomes relevant. In the right hand part of the ﬁgure the

group velocity v

, calculated from the polariton dispersion, is compared with

experimental data obtained from time-of-ﬂight measurements. Away from the

exciton resonance, the light pulses propagate through the sample with the

velocity of light in matter, the slope of the steep linear parts of the upper

10.4 P olaritons 311

(UPS) and lower polariton branches (LPB). However, close to the resonance

the group velocity is reduced by orders of magnitude, because the travelling

pulse polarizes the matter by coupling with the exciton.

After this phenomenological survey of exciton–p olaritons we turn now to

the rigorous formulation that makes use of the quantization of the electro-

magnetic ﬁeld and treats light–matter interaction as exciton–photon coupling.

The quantization of the electro-magnetic ﬁeld can b e performed analogous to

the quantization of the displacement ﬁeld in Chap.

3 (leading to phonons)

with the only diﬀerence, that in the Coulomb gauge the vector potential is

transverse (Problem 10.6). With the expansion

A(r,t)=



λ,κ

¯h

2ε

ω(κ)V

1/2

λκ



λκ

(t)+a

†

λκ

(t)



iκ·r

(10.74)

in terms of Boson operators a

λκ

for photons, the quanta of the electro-

magnetic ﬁeld, and transverse unit vectors e

λκ

with e

λκ

· κ =0,the

Hamiltonian of the radiation ﬁeld takes the expected form

rad



λ,κ

¯hω(κ)

†

λκ

(10.75)

with photon energies ¯hω(κ).

At the end of Sect.

10.3 (in the energy range of excitonic resonances) we

have formulated the Hamiltonian for the electron system in terms of exciton

operators B

νQ

. We want to extend this concept also to the light–matter inter-

action. The Ap-coupling of H

el−rad

is linear in the vector potential, which can

be replaced by its quantized form (

10.74), and it contains the electron momen-

tum operator p

. According to (

4.76) it can be expressed in terms of Fermion

operators giving



′

λ,κ

¯h

2ε

ω(κ)V

1/2

n

′

iκ·r

p · e

λκ

|nk



λκ

+ a

†

λ−κ



†

′

, (10.76)

which has the same form as the electron–phonon coupling (

8.8). Howev er,

our concern is not the coupling to an individual electron–hole pair but to an

exciton, and we should express the electron part in terms of exciton operators.

If we simplify to an exciton formed with Bloch functions from the band pair

c, v and with the wave function φ(r) for the relative motion, then the coupling

to one of the photons can be written (P

= c|e · p|v)



¯h

2ε

ω(κ)V

1/2

|φ(0)||P



+ a

†

−κ



+ B

†

−κ



, (10.77)

312 10 Light–Matter Interaction

which is linear in the Boson operators of both photons and excitons and we

may write the polariton Hamiltonian as

pol





†

+¯hω(κ)



†



+ C



+ a

†

−κ

+ a

†

−κ

+ a

†

−κ

†

−κ





(10.78)

The coupling reminds of the situation found for anti-ferromagnetic magnons in

Sect.

6.4 and can be exactly eliminated by looking for solutions with polariton

operators

= A

+ A

†

−κ

+ A

†

−κ

. (10.79)

For the detailed calculation we refer to the literature [

10, 14] and to the orig-

inal paper by Hopﬁeld [

291]. The eigenfrequencies of the polaritons are those

found with the phenomenological approach and show the anti-crossing behav-

ior (Fig.

10.7), which is typical for hybridization (see Sect. 5.4). The lower

polariton branch away from the exciton resonance is photon-like and follows

the linear dispersion, but turns over into the exciton dispersion and becomes

exciton-like. The upper polariton branch starts at the longitudinal exciton

energy but approaches for higher energy the linear dispersion of photons. The

existence of p olaritons, as coupled exciton–photon modes is clearly demon-

strated by the quoted experiments. Thus, photons propagate through the solid

as polaritons, which convert to photons when passing back into the vacuum.

This means, that absorption is not the conversion of a photon into an elec-

tronic excitation like the exciton but due to polariton scattering (e.g., with

phonons or impurities), by which energy is dissipated into other excitations

of the solid.

10.5 Light-Scattering

Light-scattering, or more precisely inelastic light scattering, has, since its dis-

covery 1928 by Raman,

gained much importance a s a spectroscopical method,

especially with the ava i lability of laser s as intense light sources. A compre-

hensive overview of the method, its applications, and the theoretical concepts

is given in a series of books with the topic Light Scattering [

118]. A schematic

view, typical for all sca ttering experiments, is shown in Fig.

10.10.

The incident monochromatic light (vector potential A

(r,t)), with photon

energy ¯hω

and photon momentum ¯hκ

, is scattered at a sample (here the

solid), and the cross section for the scattered light (vector potential A

(r,t)),

with photons of energy ¯hω

and momentum ¯hκ

, is measured. It depends on

the energy and momentum transfer

Chandrasekhara Venkata Raman 1888–1970, Nobel prize in Physics 1930.

10.5 Light-Scattering 313

Fig. 10.10. Schematic view of the light-scattering experiment

¯hω =¯hω

− ¯hω

, ¯hq =¯hκ

− ¯hκ

, (10.80)

which, under the assumption of weak light–matter interaction, i.e., validity

of the Born approximation, provides information about an elementary exci-

tation with dispersion ω(q) in the sample. The light–matter interaction can

be described by the Hamiltonian H

el−rad

of (

10.13), with the vector potential

A(r,t)=A

(r,t)+A

(r,t). The cross section depends on both the incident

and scattered radiation ﬁelds, therefore, we expect contributions linear in the

product A

not only from the ﬁrst term of H

el−rad

(Ap -coupling ) in second

order but also from the second term, which already contains this product, in

ﬁrst order perturbation theory (A

-coupling).

Fermi’s Golden Rule applied to the A

-coupling

· e

i(ω

−ω



l=1

i(κ

−κ

)·r

+ h.c. (10.81)

allows to write down immediately the transition probability

i→f

2π

¯h

· e

f|



iq·r

|i

δ(E

− E

± ¯hω) (10.82)

and the diﬀerential scattering cross section

dΩdω

¯h

2π



i,f

i→f

· e



i,f

|f|N

−q

|i|

δ(E

− E

± ¯hω). (10.83)

As can be seen from this expression, the scattering due to the A

-coupling is

caused by number ﬂuctuations N

−q



exp(iq · r

) (see Sect.

4.5)andcan

be related with the dynamic structure factor

S(q,ω)=



i,f

|f|N

−q

|i|

δ(ω

− ω

± ω)

2π



+∞

−∞

±iωt

N

(t)N

−q

(0)dt, (10.84)

314 10 Light–Matter Interaction

,hk

,h(k+q)

hω

,hκ

hω

,hκ

Fig. 10.11. Feynman diagram for the light-scattering pro cess with the A

-coupling

Stokes

anti-Stokes

hω

dωdΩ

____

∆

Fig. 10.12. Schematic picture of the scattering cross section and of the diagram

of the inv olved energy levels. The peak of the cross section at ∆ω = 0 is due to

the unscattered light, while the satellites are due to stokes (S) and anti-stokes (AS)

scattering

where E

i,f

=¯hω

i,f

, or expressed by the energy–loss function. Thus, light-

scattering, employing the A

-coupling is capable to investigate collective

modes of the solids like charg e or spin density excitations. We note in passing

that for inelastic electron scatter ing the same expression holds if e

·e

|/m

is replaced by the Coulomb interaction v

(see (

4.131). The scattering process

can also be visualized in a Feynman diagram (Fig.

10.11). The vertex of the

diagram represents the number ﬂuctuation.

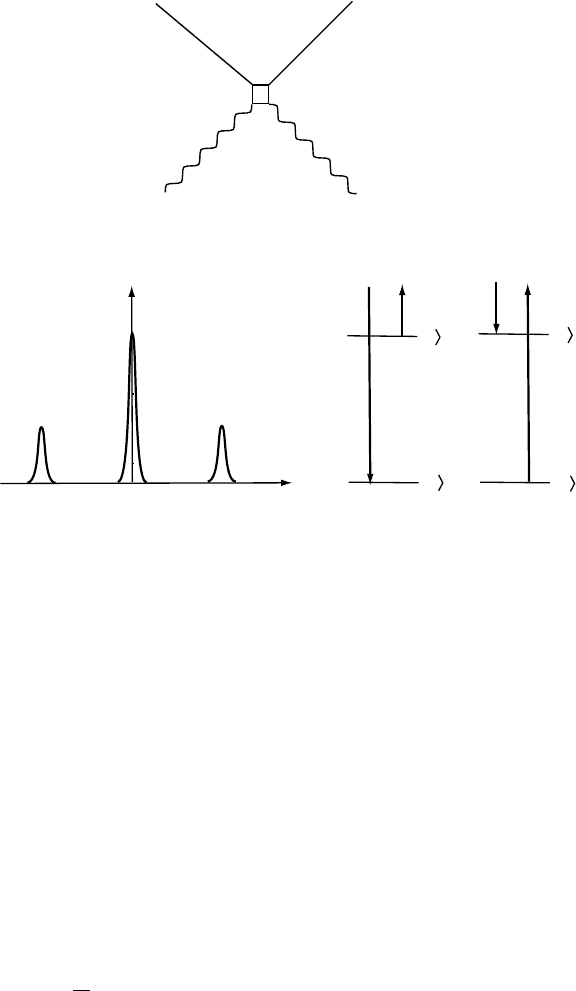
A schematic view of the s cattering cross section and the energy levels

involved in the scattering process is shown in Fig.

10.12. The central peak at

∆ω = ω − ω

+ ω

= 0 is caused by the unscattered laser light, the peaks at

positive (negative) ∆ω, called Stokes (anti-Stokes) line, result from creation

(annihilation) of an elementary excita tion in the solid.

The Ap -coupling





i(κ

·r −ω

+ e

i(κ

·r −ω



+ h.c. (10.85)

contributes in second order perturbation theory by terms linear in both vector

potentials of incident and scattered light. The cross section essentially has

10.5 Light-Scattering 315

the same structure as the one for the A

-coupling but e

· e

is replaced by

·δ

↔

·e

under the sum over initial and ﬁnal states. Here, the components

of the Raman tensor δ

↔

are given by

f|δχ

µν

|i∼



1,fz

0,zi

− E

− ¯hω

+(0↔ 1). (10.86)

In dipole approximation, the matrix elements

1,fz

= f|



−iκ

·r

lµ

|z and M

0,zi

= z|



iκ

·r

lν

|i (10.87)

reduce to the momentum matrix elements f|p

lµ

|z and z|p

lν

|i, respectively,

if the corresponding transitions are dipole allowed.

In the foregoing, the states |i, |z, |f  are to be understood as exact eigen-

states of the solid, which are not known, but can be described approximately

with the concepts developed in the earlier chapters. Let us assume the Hamil-

tonian of the solid in the form H = H

el−ph

for electrons, phonons,

and electron–phonon interaction as in Chap.

8. The eigenstates |γof H

are products of electron and phonon states in occupation number represen-

tation, while the eigenstates of H can be considered as quasi-particle states

with energies E

+iΓ

, with ﬁnite lifetime due to the interaction H

el−ph

.The

exact intermediate state |z can be expressed by the perturbation expansion

|z = |γ +



′

|γ

′

γ

′

el−ph

|γ

− E

′

+ ... (10.88)

and one obtains contributions to f|δχ

µν

|i of ﬁrst order in H

el−ph

f|δχ

µν

|i∼



γ,γ

′

fγ

γγ

′

(¯hω

− E

′

− iΓ

′

)(¯hω

− E

− iΓ

)

+(0↔ 1) , (10.89)

where M

γγ

′

= γ|H

el−ph

|γ

′

. A graphical picture of such a contribution is

shown in Fig.

10.13 together with the energy level scheme. The incoming pho-

ton creates via Ap -coupling an electron-hole pair or exciton (a), which emits

(or absorbs) a phonon (b) and recombines via Ap -coupling to the scattered

photon (c). Higher order processes with H

el−ph

are possible.

The process described here in detail is used to investigate phonons in bulk

material, quantum wells, or at surfaces. If optical phonons are involved, it

is called Raman scattering, while Brillouin scattering is due to emission or

absorption of acoustic phonons. Instead of the electron–phonon interaction as

the origin of the inelastic light-scattering, one could have also considered the

coupling between the electron system and other collective excitations like plas-

mons, plasmon–phonon mo des, or magnons to map out disp ersion. The energy

denominators in the scattering cross section can be exploited to enhance the

scattering eﬃciency by using the possible resonances of incident or scattered

light with the electronic excitation (resonant light-scattering).

316 10 Light–Matter Interaction

(a)

(b)

(c)

exciton

(a)

(b)

(c)

,hκ

hω

,hκ

Fig. 10.13. Feynman diagram and level diagram for the light-scattering process

with Ap and electron–phonon coupling

10.6 Coherent Interband Dynamics

The light–matter interaction has been treated in the previous sections of this

chapter either as a time-dependent perturbation of the electron system on a

long time scale by applying Fermi’s Golden Rule or by creating the instante-

neous formation of polaritons as coupled modes of electronic excitation and

electro-magnetic ﬁeld. In this section, we focus on the dynamics of the inter-

band transitions by looking at the light–matter system as a system of driven

oscillators or two-level systems on the very short time scale after excitation,

for which the polarization is in phase with the radiation ﬁeld. Experimentally,

the investigation of this coherent regime is possible with spectroscopy using

light pulses in the ps and fs range. The approach of this and the following sec-

tion, which, besides light–matter interaction also includes many-bo dy aspects,

provides a very general view, because previous results of this chapter can be

recovered as special cases[

95, 284, 285].

Let us start with the Hamiltonian

H = H

+ H

Coul

. (10.90)

We adopt a semiconductor in the form of a two-band model with valence and

conduction band (n = c, v) separated by a direct gap at k = 0 and formu-

late the single-particle part of the system Hamiltonia n in second quantization:



n=c,v

(k)c

†

. (10.91)

The light–matter interaction is reduced to the Ap -coupling written as

= −



k,κ



(k) · E(κ,t)c

†

vk−κ

+ h.c.



, (10.92)

with the dipole matrix element d

(k)=eck|r|vk for the transition between

the valence and conduction band states at k and the (real) electric ﬁeld vector

E(κ,t) for a harmonic wave with wave vector κ (see Problem 10.1). While

the interaction between all electrons in the ﬁlled valence band is considered

in the energies E

(k) of the Bloch states (in the vein of DFT discussed in

10.6 Coherent Interband Dynamics 317

Chap.

5), we have to explicitly consider the Coulomb interaction between the

carriers created by the primary excitation

Coul



k,k

′

q=0

†

ck+q

†

′

−q

′

+ c

†

vk+q

†

′

−q

′

+2c

†

ck+q

†

′

−q

′

. (10.93)

Further simpliﬁcations can be made with the dipole approximation, according

to which the spatial variation of the electric ﬁeld can be ignored with κ =0,

and by considering electron–hole pair transitions only close to the fundamen-

tal gap at k = 0, which all have the same dipole matrix element d

. For an

isotropic semiconductor and linear l y polarized light we may simplify d

·E(t)

to the scalar form d

E(t) and write the light–matter coupling in the form

= −



E(t)



†

+ d

∗

†



. (10.94)

Let us ﬁrst study the kinetics of optical interband transitions with-

out the Coulomb interaction. This leaves us with a single-particle problem,

which can be solved by looking at the equations of motion for the oper-

ators c

†

, and c

†

. In the Schroedinger picture these

are time-dependent operators, their thermal expectation values ρ

′

(k,t)=

c

†

(t)c

′

(t) are el ements of the time-dependent density matrix

(t)=

(k,t) ρ

(k,t)

(k,t) ρ

(k,t)

(10.95)

of a two -level system at k. We switch to the interaction picture with

O =e

¯h

−

¯h

(10.96)

and write down the equation of motion for the density matrix

¯ρ

(t)=−

¯h



(t), ¯ρ

(t)



, (10.97)

which for its elements hav e the following form (here ǫ

= E

(k)/¯h):

¯ρ

(k,t)=

¯h

E(t)e

i(ǫ

−ǫ

(¯ρ

(k,t) − ¯ρ

(k,t)) (10.98)

¯ρ

(k,t)=

¯h

E(t)



i(ǫ

−ǫ

¯ρ

(k,t) − c.c.



(10.99)

¯ρ

(k,t)=

¯h

E(t)



∗

−i(ǫ

−ǫ

¯ρ

(k,t) − c.c.



. (10.100)

318 10 Light–Matter Interaction

The diagonal elements are identical in the Schroedinger and interaction pic-

tures, ρ

(k,t)=¯ρ

(k,t), and their time derivatives are identical up to a

sign change, dρ

(k,t)/dt = −dρ

(k,t)/dt, as can be seen from (

10.99)and

(

10.100). These equations describe the interband kin etics of free carriers at k.

It will be shown later, that excitations at diﬀerent k are coupled due to H

Coul

Let us brieﬂy assume quasi-thermal equilibrium, i.e., initially created elec-

trons in the conduction band and holes in the valence band are thermalized

within their respective bands. Then, the diagonal elements of the density

matrix are Fermi–Dirac distribution functions f

and f

, respectively. For

this case, the calculation of the optical polarization P (t)=Tr(ρ(t)d), where

d is the electric dipole operator, yields the optical susceptibility χ(ω)andthe

expression for the dielectric function ε(ω) derived in Sect.

10.2 (Problem 10.7).

The more interesting case is the time scale, on which the interband excita-

tion follows the same time dependence as the driving electric ﬁeld, the c oherent

regime.Letuslookwith

E(t)=



iωt

−iωt



, (10.101)

at the equation of motion (

10.98) for the oﬀ-diagonal element of the density

matrix

¯ρ

(k,t)=e

i(ǫ

−ǫ

(k,t) , (10.102)

which takes the form

+i(ǫ

− ǫ

)

(k,t)=

¯h

E(t)(ρ

(k,t) − ρ

(k,t)) . (10.103)

The condition of almost resonant excitation with the detuning ν

= ǫ

−ǫ

−

ω is considered in the so-called rotating wave approximation by dropping the

term with exp(iωt)inE(t), which leads to

+iν

(k,t)e

iωt

= −

iω

(ρ

(k,t) − ρ

(k,t))

(k,t)=−

iω



(k,t)e

iωt

− c.c.



, (10.104)

with the Rabi

frequency ω

= d

/¯h. This set of equations is known as

coherent optical Bloch equations with reference to the Bloch equa tions used in

magnetic resonance spectroscopy. In order to s how this relation, the complex

elements of the density matrix can be used to deﬁne three real components of

a vector, the Bloch vector

(k,t)=ρ

(k,t)e

iωt

+ c.c.

(k,t)=i



(k,t)e

iωt

− c.c.



(k,t)=ρ

(k,t) − ρ

(k,t) , (10.105)

Isaac Isidor Rabi 1898–1988, Nobel prize in Physics 1944.

10.6 Coherent Interband Dynamics 319

whose time-dependence is ruled by

(k,t)=−ν

(k,t)

(k,t)=+ν

(k,t)+ω

(k,t)

(k,t)=−ω

(k,t) , (10.106)

which can also be written also in the compact form as

U(k,t)=Ω × U (k,t), (10.107)

with Ω = −ω

+ ν

. An equation of this form has been derived already

in Sect.

6.3 for the d y n amics of spins; its mechanical analogue is the equation

of motion for an angular momentum under the action of a torque.

Under resonant excitation, ν

= 0, the Bloch equation describes the rota-

tion of the Bloch vector around the −e

-axis with the Rabi frequency ω

Let us start at t = 0 with a population inversion describ ed by U (t =0)=

(0, 0 , −U

). After a half perio d, one has U (t = π/ω

)=(0, 0,U

), i.e., the ini-

tial popula tion inversion has changed its sign. This is called Rabi ﬂopping.At

the intermediate time, π/2ω

is completely converted into the component

of the Bloch vector, which is connected with the dielectric polarization

P (t). During the rotation caused by the coupling to the radiation ﬁeld, the

Bloch vector changes periodically between the components U

and U

,or

between population inversion and interband polarization, respectively.

The resonant condition cannot be fulﬁlled at the same time for inter-

band transitions at diﬀerent k, and the detuning ν

= 0 becomes important.

Let us consider a group of electron–hole pairs at diﬀerent k, but initially

with same Bloch vector U

(1)

=(0, 0,U

). A short light pulse of dura-

tion t

= π/2Ω

(so-called π/2 pulse) turns these Bloch vectors into the

2-direction, U

(2)

=(0,U

, 0), and they start to precess around the 3-direction

according to their individual detunings, i.e., the Bloch vectors run out of

phase and spread in the U

− U

plane. This spreading can b e reversed by

applying, after some time, T ,aπ pulse (duration t

= π/Ω

), which kicks

the Bloch vectors into the directions U

(3)

=(U

, −U

, 0) such that after 2T

their further precession around the 3-direction brings them all back to the

same phase with U

(4)

=(0, −U

, 0). This Bloch vector, which again is the

same for all electron–hole pairs, can be detected as emitted light pulse, the

photon echo. T he photon echo can be observed only, if the phase coherence o f

each Blo ch vector (or electron–hole excitation) with the exciting light is not

destroyed.

The coherent optical Bloch equation s exhibit some principle f eatures in

the dynamics of interband excitations, which, in reality, will be changed due

to the ﬁnite lifetime of the single-particle states and destroy phase coher-

ence. This can be considered by adding phenomenological damping terms to