R?ssler U. Solid State Theory: An Introduction
Подождите немного. Документ загружается.


370 Solutions
5.6: Proceed as in Problem 5.5 and see [
121] for the free-electron bands along Γ −L.
5.7: In the almost free-electron picture, the energy bands of Al, Si, and GaAs derive
from the free-electron bands of the fcc lattice (see Problem 5.6). Due to the differ-
ent crystal structures (Bravais lattice for Al, diamond structure for Si, zinc blende
structure for GaAs) the energy gaps are determined by different Fourier components
of the pseudo-potential:
V
psp
(r)=
n,τ
v
(τ )
psp
(r − R
0
n
− τ ) → V
psp
(G)=e
−ig·τ
v
(τ )
psp
(G).
For Al with τ = 0, the structure factor S(G)=
τ
exp (−iG · τ )equals1forall
G. For diamond and zinc blende with τ = ±τ
′
with τ
′
=(1, 1, 1)a/8 one has
V
psp
(G)=e
−iG·τ
′
v
(+)
(G)+e
iG·τ
′
v
(−)
(G)
=cos(G · τ
′
)v
S
(G) − isin(G · τ
′
)v
A
(G),
where
v
S
(G)=v
(+)
(G)+v
(−)
(G)andv
A
(G)=v
(+)
(G) − v
(−)
(G).
In Si the anti-symmetric potential v
A
(G) vanishes. Thus, Fourier components at
different reciprocal lattice vectors determine the energy bands as Al, Si, GaAs.
Especially, for G =(2, 0, 0)2π/a we have cos (G · τ ) = 0 but sin (G · τ )=1andthe
anti-symmetric potential present in GaAs removes the degeneracy of the level X
1
in
Si (see Fig.
5.11).
5.8: The crystal field splitting is determined by the matrix formed by
K
ν
′
ν
=
n
d
3
rφ
∗
ν
′ (r)v(r − R
0
n
)φ
ν
(r)
with ν = xy,yz, zx,3z
2
−r
2
,x
2
−y
2
. The p oint group operations of the cubic lattice
turn the coordinate triple x, y, z into any other permutation including sign changes
of x, y,andz, while leaving
n
v(r − R
0
n
) invariant. Thus, the groups of orbitals
d
xy
,d
yz
,d
zx
and d
3z
3
−r
2
,d
x
2
−y
2
form invariant sets under the cubic point group,
which are classified by the irreducible representations Γ
25
′
and Γ
12
, respectively,
and the matrix with the elements K
ν
′
ν
has block-diagonal form. Further inspection
shows, that each of the diagonal blocks is itself diagonal for the given basis with
identical diagonal matrix elements, thus, the crystal field splitting gives a threefold
(Γ
25
′
)andatwofold(Γ
12
) state as can b e seen at the Γ point of the band structures
depicted in Figs.
5.14 and 5.15. There is no difference between sc, bcc, and fcc crystal
structure because they have the same point group.
5.9:TheoverlapmatrixS
ν
′
ν
(k) is hermitian and can be diagonalized by a unitary
transformation U: USU
−1
= S
′
with S
′
µ
′
µ
= S
′
µ
δ
µ,µ
′
. The diagonal elements S
′
µ
of
the transformed overlap matrix represent the norms of the new basis states which
are always positive. Thus the eigenvalue equation can be rewritten
UHU
−1
H
′
UC
C
′
= EUSU
−1
S
′
UC
C
′
.
One can multiply this equation with the inverse square root of the diagonal matrix
S
′
to arrive at the eigenvalue equation
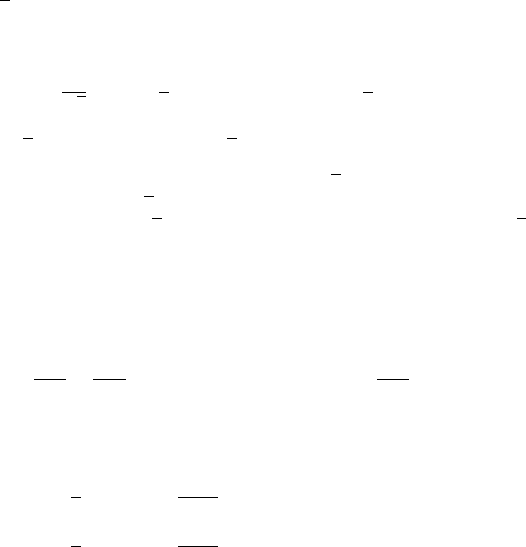
Solutions 371
S
′−1/2
H
′
S
′−1/2
S
′1/2
C
′
= ES
′1/2
C
′
and with
˜
H = S
′−1/2
H
′
S
′−1/2
,
˜
C = S
′1/2
C
′
one has the standard eigenvalue
problem with the secular equation
$
$
$
˜
H
µ
′
µ
− Eδ
µ
′
,µ
$
$
$
=0
with
˜
H = S
′−1/2
UH
′
U
−1
S
′−1/2
.
5.10: The nearest neighbors in the sc crystal structure are
R
0
n
: a(±1, 0, 0), (0, ±1, 0), (0, 0 ± 1)
leading to the dispersion
E
s
(k)=E
s
+2J
ss
(a)(cos (k
x
a)+cos(k
y
a)+cos(k
z
a))
which for k =(k, 0, 0) becomes E
s
(k)=E
s
+2J
ss
(a)cos(ka)andfork =
(k, k, k),E
s
(k)=E
s
+6J
ss
(a)cos(ka) with band widths E(0) − E((π/a,0, 0)) =
4J
ss
(a)andE(0) − E((π/a, π/a,π/a)) = 12J
ss
(a), respectively.
For the b cc crystal structure one has
R
0
n
:
a
2
(±1, ±1, ± 1), (∓1, ±1, ±1), (±1, ∓1, ± 1), (±1, ±1, ∓1)
leading to the dispersion
E
s
(k)=E
s
+2J
ss
a
√
3
!
&
cos
a
2
(k
x
+ k
y
+ k
z
)
+cos
a
2
(−k
x
+ k
y
+ k
z
)
+cos
a
2
(k
x
− k
y
+ k
z
)
+cos
a
2
(k
x
+ k
y
− k
z
)
'
which for k =(k, 0, 0) becomes E
s
(k)=E
s
+8J
ss
(a/
√
3) cos (ka/2) and for k =
(k, k, k),E
s
(k)=E
s
+2J
ss
(a/
√
3)(cos (3ka/2) + 3 cos (ka/2)) with band widths
E(0)−E((2π/a,0, 0)) = 16J
ss
(a/
√
3) and E(0)−E((π/a,π/a, π/a)) = 8J
ss
(a/
√
3).
5.11: For a solution see P.R. Wallace, Phys. Rev. 71, 622 (1947) and the article by
S.E. Louis in [
114].
5.12: Use the Peierls substitution ǫ(k) → H(p − eA)
2
with the vector potential
A =(0,B(x cos θ + z sin θ, 0)) corresponding to B = B(sin θ, 0, cos θ)towrite
H =
p
2
x
2m
t
+
1
2m
t
(p
y
− eB(x cos θ + z sin θ))
2
+
p
2
z
2m
l
.
The equations of motion for the components of the momentum are (up to terms
∼p
y
which vanish later due to ˙p
y
=0)
˙p
x
= −
i
¯h
[p
x
,H]=−
e
2
B
2
m
t
(x cos θ + z sin θ)cosθ
˙p
z
= −
i
¯h
[p
z
,H]=−
e
2
B
2
m
t
(x cos θ + z sin θ)sinθ.
Tak e the derivatives of these equation with respect to t and replace ˙x = p
x
/m
t
, ˙z =
p
z
/m
l
to obtain
372 Solutions
−¨p
x
= ω
2
t
cos
2
θp
x
+ ω
t
ω
l
sin θ cos θp
z
−¨p
z
= ω
2
t
sin θ cos θp
x
+ ω
t
ω
l
sin
2
θp
z
with ω
l,t
= eB/m
l,t
.Withp
x,z
∼ exp (−iωt) this becomes a set of homogeneous
linear equations and the eigenfrequencies follow from
$
$
$
$
ω
2
t
cos
2
θ − ω
2
ω
t
ω
l
sin θ cos θ
ω
2
t
sin θ cos θω
t
ω
l
sin
2
θ − ω
2
$
$
$
$
=0
with the nontrivial solution
ω
2
= ω
2
t
cos
2
θ + ω
t
ω
l
sin
2
θ = e
2
B
2
cos
2
θ
m
2
t
+
sin
2
θ
m
l
m
t
!
.
The expression in the bracket is the squared inverse cyclotron mass for the anisotropic
energy surface if the magnetic field includes the angle θ with the z-axis. See [
4].
5.13:Fork =(k
x
,k
y
, 0) and ∇V (001) the interface spin–orbit (or Rashba)-term
reads
H
SO
(k)=α|∇V |(k
y
σ
x
− k
x
σ
y
)
and with k
±
= k
x
± ik
y
= k exp (±iϕ)andσ
±
=(σ
x
± iσ
y
)/2
H
SO
(k, ϕ)=iα|∇V |(k
+
σ
−
− k
−
σ
+
)=iα
′
(e
iϕ
σ
−
− e
−iϕ
σ
+
).
The subband Hamiltonian with spin–orbit interaction becomes
H(k, ϕ)=
ǫ
k
iα
′
e
−iϕ
−iα
′
e
−iϕ
ǫ
k
!
.
Its eigenvalues ǫ
±
(k)=ǫ
k
± α|∇V |k do not depend on ϕ and are two parabolas
shifted against each other. Use the eigenvectors
|k, ± =
1
√
2
"
"
"
"
1
∓ie
iϕ
to calculate the expectation value of the vector of Pauli spin matrices:
k, ±|σ|k, ± = ±(e
x
sin ϕ − e
y
cos ϕ).
Thus, the spin is always oriented perpendicular to the wave vector k =(k
x
,k
y
, 0)
and rotates with ϕ. Note, that the states on each parabola form a Kramers pair.
See [
153].
Solutions for Chap.
6
6.1: Cho ose the quantum numbers for the Bloch states
α = nkσ, β =¯n
¯
k¯σ, α
′
= n
′
k
′
σ
′
,β
′
=¯n
′
¯
k
′
¯σ
′
.
After carrying out the summation over spin v ariables the matrix element reduces to
V
αββ
′
α
′
=
d
3
r
d
3
r
′
ψ
∗
nkσ
(r)ψ
∗
¯n
¯
k ¯σ
(r
′
)
e
2
κ|r − r
′
|
ψ
¯n
′
¯
k
′
σ
(r)ψ
n
′
k
′
¯σ
(r
′
).
Solutions 373
Decompose the Bloch function into plane wave and lattice periodic parts, expand
the products of periodic parts with the same argument in a Fourier series
u
∗
nkσ
(r)u
¯n
′
¯
k
′
σ
(r)=
G
B
n¯nk
¯
kσ
(G)e
iG·r
,
and use the Fourier transform of the Coulomb interaction to perform the integration
over t he space variables to find
V
αββ
′
α
′
=
G,G
′
,q
B
n¯n
′
k
¯
k
′
σ
(G)B
¯nn
′
¯
kk
′
¯σ
(G
′
)
×
e
2
ε
0
Vq
2
d
3
re
−i(k−
¯
k
′
−q−G)·r
d
3
r
′
e
−i(
¯
k−k
′
+q−G
′
)·r
′
.
For the single-band approximation set n =¯n =¯n
′
= n
′
and with only leading terms
in the Fourier series, G = G
′
=0,write
B
n¯n
′
k
¯
k
′
σ
(G) → B
kq
,B
¯nn
′
¯
kk
′
¯σ
(G
′
) → B
¯
k
q
and obtain
V
αββ
′
α
′
=
q
v(q) V
2
B
kq
B
¯
kq
δ
¯
k
′
,k−q
δ
¯
k,k
′
−q
.
6.2: To check normalization and orthogonality write
s
3
d
3
rφ
∗
nσ
(r − R)φ
n
′
σ
′
(r − R
′
)
=
1
N
δ
σ,σ
′
k,k
′
e
−ik·R−ik
′
·R
′
d
3
rψ
∗
nkσ
(r)ψ
n
′
k
′
σ
(r)
δ
n,n
′
δ
k,k
′
=
1
N
k
e
−ik·(R−R
′
)
δ
R,R
′
δ
n,n
′
= δ
n,n
′
δ
R,R
′
Thus localized functions, represented by Bloch functions, are orthogonal when cen-
tered on different sites. Insofar the Wannier representation differs from the LCAO.
Introduce fermion operators for these localized Wannier states by
c
nRσ
=
1
√
N
k
e
ik·R
c
nkσ
and calculate the anti-commutator
&
c
nRσ
,c
†
n
′
R
′
σ
′
'
=
1
N
k,k
′
e
ik·R−ik
′
·R
′
&
c
nkσ
,c
†
n
′
k
′
σ
′
'
δ
n,n
′
δ
k,k
′
δ
σ,σ
′
= δ
n,n
′
δ
σ,σ
′
1
N
k
e
ik·(R−R
′
)
= δ
n,n
′
δ
σ,σ
′
δ
R,R
′
.
The other anti-commutators yield

374 Solutions
&
c
†
nRσ
,c
†
n
′
R
′
σ
′
'
= {c
nRσ
,c
n
′
R
′
σ
′
}.
6.3: Use the representation (
6.7) of the Bloch functions to write
V
αββ
′
α
′
=
1
N
2
R
1
,R
2
,R
′
1
,R
′
2
e
−ik·R
1
e
−i
¯
k·R
2
e
i
¯
k
′
·R
′
1
e
ik
′
·R
′
2
×
d
3
r
d
3
r
′
φ
∗
(r − R
1
)φ
∗
(r
′
− R
2
)
e
2
κ|r − r
′
|
φ(r − R
′
1
)φ(r
′
− R
′
2
).
Use (
6.8) with the exponentials and sums over the wave vectors to replace the
fermion operators of Bloch states in the interaction term by those of Wannier states
to find (
6.10).
6.4: The commutator b etween c
†
↑
c
↓
and c
†
↓
c
↑
[c
†
↑
c
↓
,c
†
↓
c
↑
]=c
†
↑
c
↓
c
†
↓
c
↑
− c
†
↓
c
↑
c
†
↑
c
↓
is evaluated by using the anti-commutator for fermion operators and writing
c
†
↑
c
↓
c
†
↓
c
↑
= c
†
↑
(1 − c
†
↓
c
↓
)c
↑
= c
†
↑
c
↑
− c
†
↑
c
†
↓
c
↓
c
↑
= c
†
↑
c
↑
− c
†
↓
(1 − c
↑
c
†
↑
)c
↓
= c
†
↑
c
↑
− c
†
↓
c
↓
+ c
†
↓
c
↓
c
↑
c
†
↑
,
where the last term cancels in the commutator. Thus we have
[c
†
↑
c
↓
,c
†
↓
c
↑
]=c
†
↑
c
↑
− c
†
↓
c
↓
.
The other commutation relations
[c
†
↑
c
↓
,c
†
↑
c
↑
− c
†
↓
c
↓
]=−2c
†
↑
c
↓
, and [c
†
↓
c
↑
,c
†
↑
c
↑
− c
†
↓
c
↓
]=2c
†
↓
c
↑
follow in a similar way. These three commutators are the same as those between S
±
and S
z
and correspond to the operator algebra of the Cartesian components of the
angular momentum S
x
,S
y
,andS
z
.
6.5: Evaluate the commutator
[S
β
i
S
β
k
,S
x
j
]=S
β
k
S
x
j
S
β
i
− S
x
j
S
β
i
S
β
k
= −iε
xβγ
S
γ
j
S
β
k
δ
i,j
− S
β
i
iε
xβγ
S
γ
j
δ
j,k
,
to write the commutator of S
x
j
with the first term of the Heisenberg hamiltonian
i,k
i=k
J
ik
β
[S
β
i
S
β
k
,S
x
j
]=
+
−
k=j
β,γ
J
jk
iε
xβγ
S
γ
j
S
β
k
for i = j, k = j
−
i=j
β,γ
J
ij
iε
xβγ
S
β
i
S
γ
j
for k = j, k = i
= −i
i=j
J
ij
(S
i
× S
j
)
x
where for obtaining the last line use was made of i = k and of the meaning of the
Levi–Civita symbol. For the commutator with the second term of the Heisenberg
hamiltonian evaluate
i
[S
z
i
,S
x
j
]=
i,β
iε
zxβ
S
β
j
δ
i,j
=iS
y
j
.

Solutions 375
Putting together both contributions find
dS
x
j
dt
=
i
¯h
H
spin
,S
x
j
= −
1
¯h
i
J
ij
S
i
× S
j
x
+ gμ
B
H
ext
× S
j
x
.
6.6: Evaluate the commutator
/
α
k
,α
†
k
′
0
=
/
u
k
b
1k
− v
k
b
†
2k
,u
k
′
b
†
1k
′
− v
k
′
b
2k
′
0
= u
k
u
k
′
/
b
1k
,b
†
1k
′
0
δ
k,k
′
+v
k
v
k
′
/
b
†
2k
,b
2k
′
0
−δ
k,k
′
=
u
2
k
− v
2
k
δ
k,k
′
,
which for
u
2
k
− v
2
k
= 1 is a boson commutation relation. In the same way,
calculate
[α
k
,β
k
′
]=
/
u
k
b
1k
− v
k
b
†
2k
,u
k
′
b
2k
′
− v
k
′
b
†
1k
′
0
= −u
k
v
k
′
/
b
1k
,b
†
1k
′
0
− v
k
u
k
′
/
b
†
2k
,b
2k
′
0
=0.
The remaining commutation relations are obtained in a similar way.
6.7: Using the new boson op erators for coupled magnon–phonon modes, the
hamiltonian becomes
H
p−m
=
k
(
α
†
k
α
k
¯hω
p
k
cos
2
Θ
k
+¯hω
m
k
sin
2
Θ
k
− 2c
k
sin Θ
k
cos Θ
k
+ β
†
k
β
k
¯hω
p
k
sin
2
Θ
k
+¯hω
m
k
cos
2
Θ
k
+2c
k
sin Θ
k
cos Θ
k
+ α
†
k
β
k
(¯hω
p
k
− ¯hω
m
k
)sinΘ
k
cos Θ
k
+ c
k
cos
2
Θ
k
− sin
2
Θ
k
+ α
k
β
†
k
(¯hω
p
k
− ¯hω
m
k
)sinΘ
k
cos Θ
k
+ c
k
cos
2
Θ
k
− sin
2
Θ
k
)
.
It can be diagonalized with
¯hω
p
k
− ¯hω
m
k
sin Θ
k
cos Θ
k
+ c
k
cos
2
Θ
k
− sin
2
Θ
k
=0
or
tan 2Θ
k
=
−2c
k
¯hω
p
k
− ¯hω
m
k
.
For ω
p
k
= ω
m
k
= ω
k
we have cos
2
Θ
k
=sin
2
Θ
k
=1/2 and find for the eigenenergies
of the coupled modes
¯hω
α
k
=¯hω
k
− c
k
and ¯hω
β
k
=¯hω
k
+ c
k
and for the corresponding boson operators
α
k
=
1
√
2
a
k
− b
k
and β
k
=
1
√
2
a
k
+ b
k
.

376 Solutions
6.8: With the inverted transformation relations (
6.59) write the terms of (6.56):
b
†
1k
b
1k
= α
†
k
α
k
u
2
k
+ β
†
k
β
k
v
2
k
+
α
†
k
β
†
k
+ α
k
β
k
u
k
v
k
b
†
2k
b
2k
= β
†
k
β
k
u
2
k
+ α
k
α
†
k
v
2
k
+
β
†
k
α
†
k
+ β
k
α
k
u
k
v
k
b
†
1k
b
†
2k
=
α
†
k
α
k
+ β
k
β
†
k
u
k
v
k
+ α
†
k
β
†
k
u
2
k
+ β
k
α
k
v
2
k
b
1k
b
2k
=
α
k
α
†
k
+ β
†
k
β
k
u
k
v
k
+ α
k
β
k
u
2
k
+ β
†
k
α
†
k
v
2
k
to obtain
H
spin
≃ E
a
+2J
a
νS
k
&
α
†
k
α
k
+ β
†
k
β
k
u
2
k
+ v
2
k
+2γ
k
u
k
v
k
+
α
†
k
β
†
k
+ α
k
β
k
2u
k
v
k
+ γ
k
(u
2
k
+ v
2
k
)
+2(γ
k
u
k
v
k
+ v
2
k
'
.
Add and subtract u
2
k
under the sum to find with u
2
k
−v
2
k
= 1 the expression (
6.60).
6.9:Extend(
6.53) by the terms due to the anisotropy field H
A
and the external
field H
ext
H
spin
= J
a
n.n.ij
S
1i
· S
2j
− gμ
B
i
H
A
+ H
ext
S
z
1i
−
H
A
− H
ext
S
z
2i
and replace the spin operators by boson operators on each sublattice using the
Holstein–Primakoff transformation to obtain
H
spin
= − 2J
a
νNS
2
− 4gμ
B
H
A
NS
+2J
a
νS
k
&
b
†
1k
b
1k
+ b
†
2k
b
2k
+ γ
k
b
†
1k
b
†
2k
+ b
1k
b
2k
'
+2gμ
B
H
A
k
b
†
1k
b
1k
+ b
†
2k
b
2k
+ gμ
B
H
ext
k
b
†
1k
b
1k
− b
†
2k
b
2k
.
Eliminate the coupling between the sublattices using the Bogoliubov transformation
(
6.57) and write with the abbreviations
C = −2J
a
νNS
2
− 4gμ
B
H
A
NS , A =2J
a
νS , B =2gμ
B
H
A
,C= gμ
B
H
ext
H
spin
≃C+
k
&
Aγ
k
2u
k
v
k
α
†
k
α
k
+ β
†
k
β
k
+1
+(u
2
k
+ v
2
k
)
α
†
k
β
†
k
+ α
k
β
k
+(A + B)
(u
2
k
+ v
2
k
)
α
†
k
α
k
+ β
†
k
β
k
+2u
k
v
k
α
†
k
β
†
k
+ α
k
β
k
+2v
2
k
+ C
α
†
k
α
k
− β
†
k
β
k
'
.
Diagonalize with Aγ
k
u
2
k
+ v
2
k
= −2(A + B)u
k
v
k
. Square this relation and use
u
2
k
− v
2
k
= 1 to get a biquadratic equation for u
k
. Take its solution to find
u
2
k
+ v
2
k
= ±
(A + B)
2
(A + B)
2
− A
2
γ
2
k
1/2
,u
k
v
k
= ∓
1
2
A
2
γ
2
k
(A + B)
2
− A
2
γ
2
k
1/2
.

Solutions 377
Identify the prefactor of the magnon number operators as the magnon energy
¯hω
k
=
(
(A + B)
2
− A
2
γ
2
k
)
1/2
which without anisotropy field (B = 0) reduces to the dispersion relation for the
antiferromagnetic magnons which for small k is linear. With anisotropy field one
finds a finite magnon energy for k = 0 and a quadratic dispersion for small k as can
be seen in Fig.
6.8.
6.10: Ev a luate for lo w temperature (T ≪ T
C
) the magnetization (per unit volume)
M(T )=gμ
B
NS −
k
b
†
k
b
k
or
M(0) − M(T )=gμ
B
k
1
exp (¯hω
k
/k
B
T ) − 1
= gμ
B
4π
(2π)
3
∞
0
k
2
dk
exp (Dk
2
/k
B
T ) − 1
where the quadratic dispersion for small k is used. The integral (it is a Bose integral)
can be solved as described in the Appendix (
A.3) to yield Bloch’s T
3/2
law:
M(0) − M(T )=ζ(
3
2
)
gμ
B
M(0)
k
B
4πD
!
3/2
T
3/2
.
See [
166].
6.11: Calculate the exp ectation value in (
6.106)forT =0:
...
0
=
m
(
Ψ
0
|M
+
(q,τ)|Ψ
m
Ψ
m
|M
−
(−q, 0)|Ψ
0
−Ψ
0
|M
−
(−q, 0)|Ψ
m
Ψ
m
|M
+
(q,τ)|Ψ
0
)
.
Replace the operators M
±
by the fermion operators and extract the exponentials
with the time dependence. The energy difference E
m
− E
0
of exact eigenstates
b ecomes in HF approximation the energy difference of single-particle energies for
particle–hole excitations with spin-flip across the Fermi energy. By manipulations
as in Sect.
4.5 one arrives at the spin susceptibility (6.108).
To evaluate (
6.108), use
ǫ
k+q↑
− ǫ
k↓
= −∆+
¯h
2
m
k · q + ǫ
q
,ǫ
k↑
− ǫ
k−q ↓
= −∆+
¯h
2
m
k · q − ǫ
q
with ǫ
q
=¯h
2
q
2
/2m and perform the sum over k with the substitution k · q =
kq cos θ, cos θ = x. The first term can b e written
A
↓
=
|k|≤k
F↓
1
¯hω + ǫ
k+q↑
− ǫ
k↓
=
V
(2π)
2
k
F
↓
0
dkk
2
+1
−1
1
¯hω − ∆+ǫ
q
+¯h
2
kqx/m
dx.

378 Solutions
The integral over x can be solved according to
+1
−1
dx
a + bx
=
1
b
a+b
a−b
dz
z
=
1
b
ln
"
"
"
"
1+b/a
1 − b/a
"
"
"
"
.
Looking for collective excitations at small q one has b/a ≪ 1andcanusethe
expansion
1
b
ln
"
"
"
"
1+b/a
1 − b/a
"
"
"
"
≃
2
b
+
b
a
+
1
3
b
a
!
3
,
=
2
a
+
1+
1
3
b
a
!
2
,
to obtain
A
↓
=
2V
(2π)
2
1
¯hω − ∆+ǫ
q
k
−
F
0
dkk
2
+
1+
k
2
3
¯h
2
q
m
!
2
1
¯hω − ∆+ǫ
q
!
2
,
.
After integration and corresponding evaluation of the second term A
↑
one arrives
at (
6.108).
Solutions for Chap.
7
7.1: Evaluate the commutator [c
¯
k,¯σ
,c
†
k+qσ
c
†
k
′
−qσ
′
c
k
′
σ
′
c
kσ
] by successively inter-
changing c
¯
k,¯σ
with the four operators appearing in the interaction term. Each step
leads to a change in sign and in addition gives a Kronecker δ for exchange with the
creation operators, thus
c
¯
k,¯σ
c
†
k+qσ
c
†
k
′
−qσ
′
c
k
′
σ
′
c
kσ
= δ
¯
k,k+q
δ
¯σ,σ
c
†
k
′
−qσ
′
c
k
′
σ
′
c
kσ
− δ
¯
k,k
′
−q
c
†
k+qσ
c
k
′
σ
′
c
kσ
.
Interchange the last two operators in the second term and replace σ by σ
′
and k by
k
′
. Replace in the first term q by −q and consider the properties of the interaction
matrix element to find the expression for [c
¯
k
, H
int
](
7.20). The commutator [c
†
¯
k
, H
int
]
is evaluated by analogous steps.
7.2: The equation of motion of the full Green function G(kσ; t − t
′
)(
7.21)canbe
writtenwith(
7.23)as
i¯h
∂
∂t
− ǫ
kσ
!
G(kσ; t − t
′
)=δ(t − t
′
)+
dt
′′
Σ(kσ; t − t
′′
)G(kσ; t
′′
− t
′
).
Replace the Green function and the self-energy by their Fourier transform with
respect to the time arguments and identify the integrands to obtain
(¯hω − ǫ
kσ
) G(kσ; ω)=1+Σ(kσ; ω)G(kσ; ω).
After multiplication with the Green function of the noninteracting system
G
0
(kσ; ω)=(¯hω − ǫ
kσ
)
−1
one arrives at the Dyson equation
G(kσ; ω)=G
0
(kσ; ω)+G
0
(kσ; ω)Σ(kσ; ω)G(kσ; ω).
7.3: The commutator of n
i−σ
c
iσ
with the single-particle part H
0
yields three terms
due to interchange of creation and annihilation operators:
Solutions 379
[n
i−σ
c
iσ
,H
0
]=
mjσ
′
t
mj
c
†
i−σ
c
i−σ
c
iσ
c
†
mσ
′
c
jσ
′
− c
†
mσ
′
c
jσ
′
c
†
i−σ
c
i−σ
c
iσ
=
mjσ
′
t
mj
δ
im
δ
σσ
′
n
i−σ
c
jσ
− δ
im
δ
σ−σ
′
c
†
i−σ
c
iσ
c
j−σ
− δ
ij
δ
σ−σ
′
c
†
m−σ
c
i−σ
c
iσ
=
m
t
im
n
i−σ
c
mσ
+ c
†
i−σ
c
m−σ
c
iσ
− c
†
m−σ
c
i−σ
c
iσ
,
where the last line is obtained by prop er choice of the summation indices and
rearranging the operators. Similarly the commutator with the interaction term is
evaluated
[n
i−σ
c
iσ
,H
1
]=
1
2
U
mσ
′
(n
i−σ
c
iσ
n
mσ
′
n
m−σ
′
− n
mσ
′
n
m−σ
′
n
i−σ
c
iσ
)
=
1
2
U
mσ
′
n
i−σ
c
iσ
c
†
mσ
′
c
mσ
′
n
m−σ
′
− n
mσ
′
n
m−σ
′
c
iσ
=
1
2
U
mσ
′
n
i−σ
(δ
im
δ
σσ
′
c
iσ
n
i−σ
+ δ
im
δ
σ−σ
′
n
i−σ
c
iσ
) ,
which using n
2
i−σ
= n
i−σ
becomes (
7.55).
7.4: Calculate the derivative of the self-energy (
7.70) and obtain the spectral weight
Z(E)=
1 −
∂Σ
∂E
!
−1
=
E − ǫ
0
− U(1 −n
−σ
)
2
E − ǫ
0
− U(1 −n
−σ
)
2
+ U
2
n
−σ
(1 −n
−σ
)
.
For the lower Hubbard band with E = ǫ
0
+2t cos ka this becomes
Z
lower
=
2t cos ka − U(1 −n
−σ
)
2
2t cos ka − U(1 −n
−σ
)
2
+ U
2
n
−σ
(1 −n
−σ
)
and reduces for k = π/2a to Z
lower
=1−n
−σ
. For the upp er Hubbard band with
E = ǫ
0
+ U +2t cos ka the result is
Z
upper
=
2t cos ka + Un
−σ
2
2t cos ka + Un
−σ
2
+ U
2
n
−σ
(1 −n
−σ
)
and Z
upper
= n
−σ
for k = π/2a. Note that the spectral weights for k = π/2a are
those of the atomic limit (see Fig. 7.3).
7.5: This problem is solved in some detail in [
169, 206]. It leads to the so-called t−J
model, where t is the hopping integral and J ∼ t
2
/U is the effective exchange matrix
element.
7.6: Describing the delocalized electrons by fermion operators c
†
kσ
,c
kσ
in a band
with dispersion ǫ
k
and the localized electrons with energy ǫ
d
by fermion operators
d
†
σ
,d
σ
, the Hamiltonian is formulated as
H =
k,σ
ǫ
k
c
†
kσ
c
kσ
+
σ
ǫ
d
d
†
σ
d
σ
+
k,σ
V
kσ
d
†
σ
c
kσ
+ c
†
kσ
d
σ
+ Un
d
↑
n
d
↓
.
