Рубин А.Б., Шинкарев В.П. Транспорт электронов в биологических системах

Подождите немного. Документ загружается.

ятности первого состояния, согласно формуле

(7.10)

можно

написать

•'

<РЛ*)<:—+

\Pi (0) — —1

е-

101

Мы

видим, что стационарная оценка в данном

случае

является

неэффективной.

Это значит, что, используя локальный подход,

когда вероятность интересующего нас состояния оценивается ис-

ходя лишь из уравнения для этого состояния, а в самой оценке

фигурируют лишь константы скорости «притока» и

«оттока»

для

данного состояния, нельзя рассчитывать на то, что верхняя оцен-

ка

даст

значение, близкое к истинному. Она может лишь указать

тот предельный уровень, выше которого стационарная заселен-

ность данного состояния быть не может. Совершенно очевидно,

что если стационарная вероятность состояния, переходящего в

первое состояние с константой скорости 100, равна нулю, то и

вероятность первого состояния также равна нулю. 2. Пусть граф

состоянии комплекса имеет вид:

—*•()-*•

Для вероятности пер-

вого состояния, согласно выражению (7.10), можно написать:

1/Ю0 + [МО) — 1/Ю1]

е-

101

В рассматриваемом

случае

эффективной является как нижняя,

так и верхняя оценки. Следовательно, здесь локальный

подход

позволяет достаточно хорошо оценить вероятность рассматривае-

мого состояния. Заметим, что согласно выражению (7.6) величи-

на

верхней оценки не изменится, если считать, что в первое со-

стояние переходит произвольное число состояний с константами

скорости, меньшими, чем 1. Действительно, в этом

случае

макси-

мальная из констант скорости «притока» в данное состояние по-

прежнему равна 1, и, таким образом, величина оценки не изме-

нится.

3. В качестве последнего примера рассмотрим граф со-

стояний

комплекса, у которого к интересующему нас 1-му состоя-

нию подходит 100 состояний с одинаковыми константами скоро-

сти, а оно в свою очередь переходит в 20

других

состояний с те-

ми

же константами скорости.

1001.

Тогда неравенство

(7.10)

для вероятности застать комплекс в

1-м состоянии в момент времени t имеет вид

0< 1/21

Вероятность состояния I в стационарном состоянии не превыша-

ет 1/21. На первый взгляд полученный

результат

несколько не-

151

обычен, поскольку интуитивно кажется, что в рассматриваемом

случае

стационарная вероятность должна быть близка к едини-

це,

вследствие того что число состояний, в которые оно перехо-

дит, существенно меньше числа состояний, которые переходят в

1-е состояние, а величины констант скорости в обоих случаях

одинаковы.

Полученный

результат

находит простое объяснение.

Исходя из схемы

существует

по крайней мере 100 отличных от

/-го состояний с ненулевыми вероятностями застать в них комп-

лекс.

Поскольку сумма

всех

вероятностей комплекса равна еди-

нице,

то это приводит к уменьшению вероятности /-го состояния.

Прежде чем вывести оценки для вероятности суммы состоя-

ний,

отметим, что в силу несовместности отдельных состояний

комплекса

вероятность суммы состояний равна сумме вероятно-

стей состояний. Это позволяет для получения необходимых оце-

нок

воспользоваться системой дифференциальных уравнений

(7.1). Кроме того, отметим также тот простой факт, что если име-

ется верхняя оценка для суммы вероятностей, то эта же оценка

справедлива и для каждого слагаемого и, наоборот, из нижней

оценки

для одного слагаемого

следует

справедливость этой оцен-

ки

и для всей суммы.

Совершенно

аналогично тому как это было сделано при вы-

воде неравенства (7.10), можно получить верхнюю и нижнюю

оценки

и для вероятности суммы произвольных г состояний комп-

лекса

P(5

+S,-

... + S

, t),

l<i

...

<n,

суммируя

необходимые уравнения из системы уравнений (7.1).

Для

удобства

обозначений

будем

считать, что нам необходи-

мо получить оценку лишь для вероятности суммы первых г со-

стояний.

Просуммировав дифференциальные уравнения (7.1)

для вероятностей p

i=\, 2, .. ., г этих состояний и приводя по-

добные члены, получим дифференциальное уравнение для сум-

мы этих вероятностей:

d(Pi+

•••

pr)/dt

= —

+ • • • —

knPr

Здесь k'

—сумма

всех

констант скорости, с которыми £-е со-

стояние

(l<i«:r) переходит в состояния, не принадлежащие вы-

деленным r-состояниям. Исходя из выражения

(7.12)

выведем

оценки

для суммы вероятностей р

..., р

. Среди вероятностей

Pi, j>r нет вероятностей таких, что их индексы меньше г, поэто-

му, пользуясь неравенством

1>'

1—1

следующим из условия нормировки

152 ;

(7.14)

а также тем, что

' +

• • •

можно получить дифференциальное неравенство для суммы ве-

роятностей:

где а!— максимальная из сумм констант скорости, с которыми

комплекс переходит в выделенные г состояний исходя из осталь-

ных состояний; Ь

— минимальная из сумм констант скорости, с

которыми выделенные г состояний переходят во все остальные

состояния.

Решая это дифференциальное неравенство, получим

верхнюю оценку для вероятности суммы состояний [Шинкарев,

1978; Венедиктов, Шинкарев, 1979]:

(7.15)

Здесь

Все сказанное выше для вероятности отдельного состояния

дословно переносится на рассматриваемый случай.

В качестве примера применения оценки

(7.15)

рассмотрим

граф состояний, соответствующий переносу электронов в комп-

лексе

трех

одноэлектронных переносчиков в отсутствие коопера-

тивное™

Найдем оценку для состояний 100 и 101, из которых возмо-

жен переход по константе скорости k

. В эти два состояния

ведут

153

константы скорости k

и k

, поэтому а

=тах (k

). Рассматри-

ваемые состояния 5 и 6 переходят в остальные состояния с кон-

стантами скорости k

, поэтому bi=ki. Следовательно, согласно

формуле

(7.15)

имеем

, k

)

*2 -f max (k

Это неравенство показывает, что если константа скорости k

су-

щественно больше констант скорости k

{

и k

, то вероятность сум-

мы рассматриваемых состояний пренебрежимо мала, начиная со

времени т~ \\к

7.2. Рекуррентный метод получения оценок

Одним из возможных способов получения оценок является

рекуррентный метод, когда для получения новых оценок исполь-

зуются уже ранее найденные. В отличие от изложенного выше

метода нахождения локальных оценок, он предполагает извест-

ным

если не весь граф состояний, то по крайней мере его доста-

точно большую часть. В связи с этим его рационально применять

случае

не очень сложных схем.

Рассмотрим граф состояний комплекса, имеющий следующий

вид:

...-+п%.

(7.16)

jmi \m, |т, \

Такого рода схема переходов состояний комплекса, как мы уви-

дим далее, часто встречается при анализе переходных процессов

при

фотосинтезе. Кроме того, она представляет самостоятельный

интерес, поскольку часто возникает при кинетическом анализе

переходных процессов в ферментативных реакциях [Березин,

Варфоломеев, 1979], а также при анализе надежности различ-

ного рода систем [Гнеденко и др., 1965; Соловьев, 1975; Березин,

Варфоломеев, 1979]. Если на этой

схеме

положить все

rrii

— O,

то

получится система последовательных мономолекулярных реак-

ций,

для которой известно как точное решение [Бартлетт, 1958;

Родигин, Родигина, 1960; Бенсон, 1964], так и различного рода

оценки

[Гнеденко и др., 1965; Соловьев, 1975].

Точное

решение

Будем предполагать, что все k

+ trii—различные. Система

дифференциальных уравнений, описывающая переходы, проис-

ходящие согласно

схеме

(7.1), имеет следующий вид:

/dt=k

—(k

, i=\,2.

..., п.

(7.17)

154

Здесь по определению положено &

= 0. Ниже

будем

предпола-

гать, что начальные условия для рассматриваемой системы

уравнений

имеют вид:

/?,(())

= 1,

р,(0)=0,

i>2. (7.18)

Как

можно проверить по индукции, решением системы урав-

нений

(7.17) с начальными условиями (7.18) является следую-

щее выражение:

(0 = КК

• • •

kt-i 2 -i-i-, i = 1, 2, ..., п,

(7.19)

здесь

= k

+ m

; ы

{

(— Я,,)

(Я,,—Я,.) (Я,

—Я,)

...

(Я,,-,—Я,»)

Х(Я.1+1—

Я,,)

...

(Я,(—Я,,). Полученное решение, хотя

элементар-

но,

однако имеет достаточно громоздкий

вид и

труднопримени-

мо

при

больших

п. В

связи

этим ниже выведены простые нера-

венства, которые позволяют оценить кинетическое поведение

от-

дельных переменных.

Вывод

оценок

[Шинкарев,

1982]

Обозначим

через M

и m

соответственно максимальную и ми-

нимальную из величин (ki+rrii):

= max (k

(

+ mi), m

= min (ki + mi). (7.20)

Подставляя

в систему уравнений (7.17) вместо величин k

{

величины

и m

, получим следующую систему дифференциаль-

ных неравенств:

kt-ipi-i

—

Mgpi

< pt <

kuxPi-x

—

pi,

* = 1,2, .... q. (7.21)

Рассмотрим

сначала правые неравенства. Вводя новые перемен-

ные

(

=р<е"У, i= 1,2, q, правые неравенства можно перепи-

сать в виде

*,_„

i=l, 2,

...,q.

(7.22)

Так

как k

= 0, то решением первого неравенства в формуле

(7.22) является

*,<*,(())

=р,(0)

= 1. (7.23)

Легко видеть, что *Д0)

=рД0)=О,

i>\, поэтому из формулы

(7.22)

следует,

что

(7.24)

Итерируя

последовательно соотношение (7.24) с учетом (7.23),

155

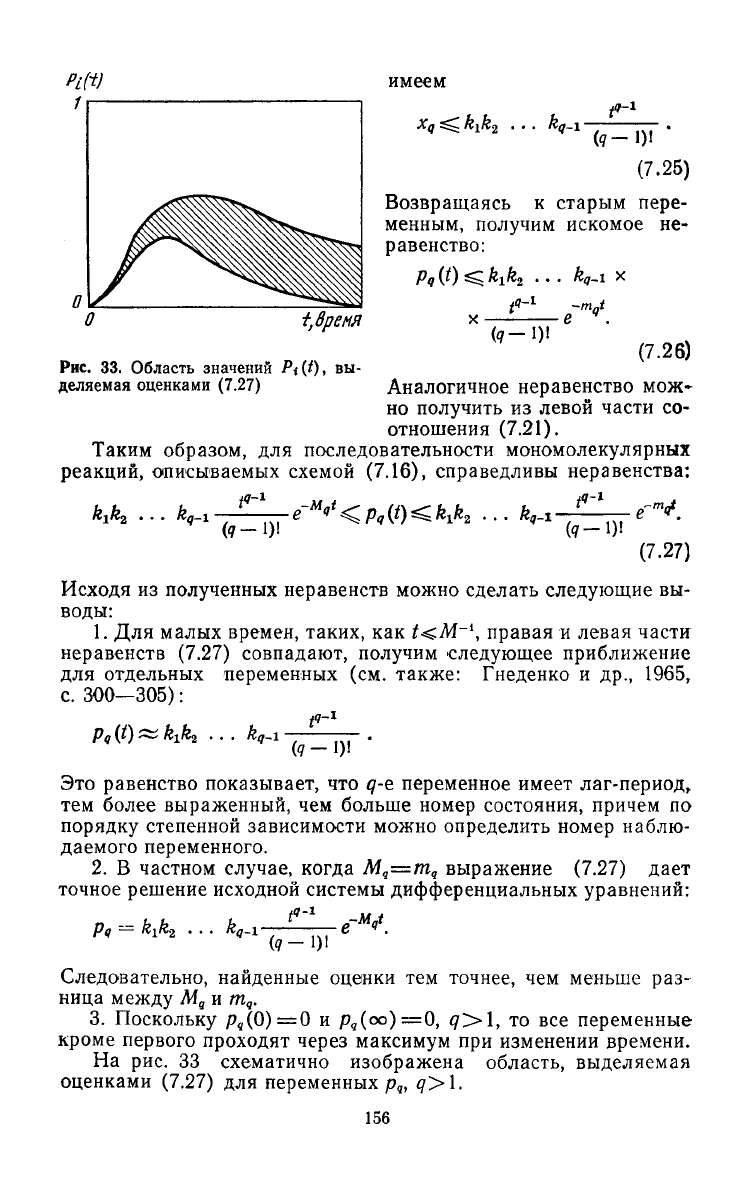
имеем

(9-1)1

(7.25)

Возвращаясь

старым пере-

менным,

получим искомое

не-

равенство:

МО'

время

Рис.

33. Область

значений

Р<(0.

вы

деляемая

оценками

(7.27)

-v

(9-1)1

(7.26)

Аналогичное неравенство мож-

но

получить

из

левой части со-

отношения

(7.21).

Таким

образом,

для

последовательности мономолекулярных

реакций,

описываемых схемой (7.16), справедливы неравенства:

-i

(9-1)1

(9-1)'

(7.27)

Исходя

из

полученных неравенств можно сделать следующие вы-

воды:

1. Для малых времен, таких, как

^<М~',

правая

левая части

неравенств

(7.27)

совпадают, получим следующее приближение

для отдельных переменных (см. также: Гнеденко

др.,

1965,

с.

300—305):

q-l

Pq(t) ЯК

&Л . . .

kq-1

_ .

Это равенство показывает, что q-e переменное имеет лаг-период,

тем более выраженный, чем больше номер состояния, причем

по

порядку степенной зависимости можно определить номер наблю-

даемого переменного.

частном случае, когда M

выражение

(7.27)

дает

точное решение исходной системы дифференциальных уравнений:

Следовательно, найденные оценки

тем

точнее,

чем

меньше

раз-

ница

между

и т

3. Поскольку

р„(0)=0

(оо)=0,

<7>1,

то все

переменные

кроме первого проходят через максимум при изменении времени.

На

рис.

схематично изображена область, выделяемая

оценками

(7.27)

для переменных

, q>\.

156

7.3.

Оценки

для

стационарных

вероятностей

Для стационарных вероятностей состояний комплекса

могут

быть получены оценки, отличные от тех, которые являются пре-

дельными для экспоненциальных. Это связано с возможностью

использовать для их получения систему линейных алгебраичес-

ких уравнений относительно стационарных вероятностей.

Верхние

стационарные

оценки

Исходя из формулы (7.1) для стационарных вероятностей

можно записать

следующую

систему линейных алгебраических

уравнений:

2 O, (7.28)

где

= 2

Чтобы получить оценку для стационарной вероятности того

или иного состояния можно воспользоваться любым уравнением,.

Рис.

34. К выводу неравенства

(7.32)

куда

входит

эта вероятность. Несложно видеть, что стационар-

ная

вероятность p

фигурирует как в условии стационарности

для самого i-ro состояния:

-*«Р*

+ 2%»/ = 0, (7.29)

так и в качестве слагаемого в уравнениях для вероятностей тех

состояний,

в которые переходит t-e состояние:

—*nPi

+ *«Pi+ ... =0, 1фи

(7.30)

Ранее мы уже использовали уравнение

(7.29)

для получения

стационарных оценок — они были предельными для экспоненци-

альных. Сейчас мы выведем оценки для вероятности i-ro состоя-

ния,

применяя условие стационарности

(7.30)

для тех состояний,

в которые переходит i-e состояние (рис. 34).

Пренебрегая в условии стационарности

(7.30)

всеми членами,

кроме k

{

, получим

kuPi^krf,.

(7.21)

Учитывая теперь, что в силу условия нормировки (7.3)

<\—р

{

157

для вероятности р

{

можем записать

Таким образом стационарная вероятность застать комплекс в

/-том состоянии не превосходит суммы

всех

констант скорости

«оттока»

из соседнего по

выходу

состояния, деленной на

сумму

этой суммы и константы скорости перехода из i-ro состояния в

1-е.

Рассмотрим пример применения полученного неравенства.

Пусть граф переходов имеет вид

100 100 I

—>-1

—*•

2 —••.

Сумма

всех

констант скорости оттока из второго состояния рав-

на

1, поэтому для вероятности интересующего нас первого со-

стояния

получим р,= 1/(1 +100) =

1/100.

Пример иллюстрирует

тот случай, когда использование выведенной ранее стационар-

ной

оценки (7.7) малоэффективно, а использование оценки

(7.32)

позволяет значительно лучше оценить вероятность перво-

го состояния. Фактически это связано с тем, что при получении

оценки

(7.32)

учтена информация о состояниях, соседних с ин-

тересующим нас состоянием. Можно попытаться за счет расши-

рения

числа используемых для получения оценок алгебраических

уравнений улучшить полученные ранее оценки. Ниже для полу-

чения

оценок используются не только отдельные уравнения, но

их суммы.

Метод

контура

Система дифференциальных уравнений (7.1) есть условие не-

прерывности в пространстве состояний — изменение во времени

заселенности какого-либо состояния обусловлено переходом ком-

плекса из данного состояния и приходом в него из

других

состоя-

ний.

В стационарных условиях для каждого состояния наблюда-

ется равенство скоростей «притока» и

«оттока».

Геометрически

можно считать, что записывается условие стационарности для

замкнутого контура f, окружающего выделенное состояние. На-

пример, если контур Y окружает состояние 2

то в контур

входит

поток

pi,

а выходит k

. Условие стацио-

нарности для контура ч запишется так же, как для состояния 2:

А^=&

. Окружим контуром 7 не одно, а два состояния, на-

пример состояния 2 и 3.

158

Рис.

35. К выводу неравенства (7.36) Рис. 36. К выводу неравенства (7.37)

В данном

случае

условие стационарности запишется как

(7.33)

Очевидно, потоки, находящиеся внутри контура, в этом

случае

учитывать не надо, поскольку они взаимно уничтожаются. Фак-

тически выражение

(7.33)

получается при сложении условий

стационарности для состояний 2 и 3. Однако если число состоя-

ний

достаточно велико, то графический метод может оказаться

более предпочтительней, ввиду его наглядности. Выбирая опре-

деленным образом контуры, можно получить необходимые для

проведения оценок условия стационарности.

Более общие, чем полученные выше, оценки можно вывести

из

условия стационарности для контура •у. Для того чтобы мож-

но

было получить оценку для стационарной вероятности р

не-

обходимо, чтобы контур содержал внутри себя интересующее

нас состояние i либо чтобы это состояние могло переходить в од-

но

из состояний контура у. Рассмотрим более подробно процесс

получения оценок. Пусть интересующее нас состояние i находит-

ся

внутри контура f и имеется состояние т вне f, в которое пе-

реходит состояние i (рис. 35). Условие стационарности для кон-

тура,

удовлетворяющего этому требованию, имеет вид:

• • •

+pX=kp

+ ...

(7.34)

Здесь k — сумма констант скорости, с которыми состояние i пере-

ходит

в состояния, не принадлежащие ч; /г„ ..., k

—суммы кон-

стант скорости, с которыми переходят состояния, не входящие в

контур -у, в состояния, входящие в него. Учитывая закон сохра-

нения

и следующее из него неравенство p

+ ... +р

= \—р

по-

следовательно имеем

< max kj (p

•

(7.35)

159

Таким образом, для вероятности застать комплекс в состоянии

имеем

следующую

оценку:

< max

fc//(max

It,-

+ k),

(7.36)

т. е. стационарная вероятность p

не больше максимальной из

сумм констант скорости перехода состояний, находящихся вне

If, в состояния, принадлежащие if, деленной на

сумму

всех

кон-

стант скорости

«вытока»

состояния i из контура f и указанной

выше максимальной суммы констант скорости «притока» в кон-

тур f. Ясно, что полученная оценка совпадает с полученной вы-

ше оценкой (7.7), если контур •у окружает лишь одно £-е состоя-

ние.

Совершенно аналогично из рассмотрения случая, когда ин-

тересующее нас состояние переходит в одно из состояний конту-

ра (рис. 36), можно получить

следующую

оценку:

(7.37)

где а — максимальная из сумм констант скорости, с которыми

состояния,

принадлежащие контуру к, переходят в состояние вне

f, a k

— константа скорости, с которой интересующее нас состоя-

ние

переходит в контур у.

Ясно,

что выведенные здесь оценки для стационарных веро-

ятностей являются обобщением неравенств (7.7) и

(7.32)

соот-

ветственно.

Рассмотрим пример применения выведенных неравенств.

Пусть нам необходимо оценить вероятность третьего состояния

на

графе

Исходя из контура -у, для вероятности р

получим согласно фор-

муле

(7.37):p

<:*

/(fe

+fe

Аналогично исходя из контура f

получим согласно формуле

(7.36)

<max(ki,

)Amax(^

) + fe

+&,]. Если задана опре-

деленная иерархия величин констант скорости, то соответствую-

щим выбором контура можно добиться того, что оценка веро-

ятности интересующего нас состояния

будет

весьма эффектив-

ной.

160