Рубин А.Б., Шинкарев В.П. Транспорт электронов в биологических системах

Подождите немного. Документ загружается.

состояний комплекса конечно, то на каком-то (<7+1-)м шаге нач-

нутся повторения одних и тех же состояний, т. е. получится не-

кий

цикл F. Назовем состояния i, и (i).

• •

•, /»-i (0 и указанный

цикл

F квазисостояниями первого ранга, порожденными состоя-

нием

i. В

результате

последовательного применения данной про-

цедуры множество

всех

состояний комплекса разобьется на ква-

зисостояния первого ранга, которыми являются как построен-

ные циклы, так и состояния комплекса, не входящие ни в один

из

циклов.

Для того чтобы задать укрупненную цепь, достаточно ука-

зать, как вычисляются константы скорости выхода из цикличе-

ских квазисостояний, поскольку все остальные квазисостояния

совпадают с состояниями комплекса. Как легко понять, вычис-

ление констант выхода из квазисостояний нужно производить по

следующему плану. Сначала вычисляется стационарное распре-

деление вероятностей на состояниях, принадлежащих некоторо-

му изолированному циклическому квазисостоянию F, при пред-

положении, что

существуют

только переходы

между

состояния-

ми,

принадлежащими F, а константы скорости переходов в до-

полнение к этому квазисостоянию равны нулю.

Пусть р

, ..., р

есть указанное стационарное распреде-

ление вероятностей на F; г — число состояний в F. Тогда кон-

станта скорости перехода из F, в не принадлежащее F состоя-

ние,

с номером т имеет вид

(8.14)

где k

—константы скорости перехода из состояния /ef в со-

стояние т, m(£F. Из формулы

(8.14)

следует,

что среднее время

выхода из данного квазисостояния F равно

т —.

(8.15)

Если имеется иерархия величин констант скорости переходов

между

уже построенными квазисостояниями первого ранга, то

можно получить квазисостояния второго ранга, применив ука-

занную процедуру к квазисостояниям первого ранга и т. д.

Полученная редуцированная цепь также является марков-

ской,

но с новыми константами переходов

между

квазисостоя-

ниями

[Королюк, Турбин, 1976]. Эффективность процедуры вы-

деления квазисостояний, очевидно, связана с иерархией величин

констант скорости; чем больше по порядку отличаются величины

констант скорости, тем точнее функционирование комплекса опи-

сывается через квазисостояния. Поясним это на примере. Оценка

приближения может быть получена из сравнений вероятности

остаться после одного

«оборота»

в данном циклическом квази-

181

состоянии F с вероятностью

выхода

из него. Пусть квазисостоя-

ние

F имеет вид

"•--Г.

_>•••

(8.16)

где /п,-—константы скорости

выхода

из данного квазисостояния,

— соответствующие константы скорости перехода в состояния,

принадлежащие данному квазисостоянию F. Тогда вероятность

остаться в данном квазисостоянии за один

«оборот»,

исходя, на-

пример,

из 1-го состояния, равна —

•

— ... —.

ki~\-m

-\- т

-j-

Выделение данного квазисостояния оправдано, если эта величи-

на

близка к единице.

Следует

отметить, что предложенная конструкция [см. так-

же: Вентцель, Фрейдлин, 1979], с одной стороны, представляет

перенесение на случайный процесс принципа усреднения [Бого-

любов, Митропольский, 1974], а с

другой

— если перейти к рас-

смотрению распределения этого процесса, то она является ана-

логом известной теоремы Тихонова о быстрых и медленных пе-

ременных [Васильева, Бутузов, 1973]. В частном

случае

стацио-

нарной

ферментативной кинетики подобный метод был предло-

жен в работе [Cha, 1968], где квазисостояниям отвечали

участ-

ки

«быстрого наступления равновесия».

8.3.

Состояния

комплекса,

достижимые

за

время

наблюдения

Число различных состояний комплекса экспоненциально воз-

растает при увеличении числа переносчиков, однако при задан-

ном

соотношении величин констант скорости не все из возмож-

ных состояний комплекса реализуются за время наблюдения.

Очевидно, что, чем меньше рассматриваемый промежуток вре-

мени,

тем меньшее число состояний комплекса может быть до-

стигнуто исходя из некоторого фиксированного начального со-

стояния.

Оценив время

выхода

из квазисостояния F, можно ука-

зать то множество квазисостояний, которое доступно комплексу

на

данных временах рассмотрения. Следовательно, множество

состояний,

которое необходимо рассматривать для описания

функционирования

комплекса, зависит как от начальных усло-

вий,

так и от времени наблюдения за комплексом. Часто началь-

ные условия таковы, что за интересующее нас время комплекс,

изначально находясь в каком-то квазисостоянии F, не успевает

выйти из него, и

тогда

для описания работы такого комплекса

достаточно ограничиться множеством состояний, принадлежащих

F. Рассмотрение только переходов

между

состояниями F пред-

ставляет собой значительное упрощение.

182

Таким образом, на малых временах достаточно рассмотре-

ния

небольшого числа состояний,

которые комплекс может по-

пасть за это время; на больших интервалах времени увеличива-

ется число состояний, доступных комплексу, однако при описании

функционирования

комплекса уже возможен переход от состоя-

ний

квазисостояниям

рассмотрение эволюции квазисостоя-

ний.

Следовательно, несмотря на увеличение числа доступных

комплексу состояний,

удается

уменьшить объем фазового про-

странства путем введения квазисостояний.

8.4.

Пример.

Нециклический

транспорт

электронов

хроматофорах

пурпурных

бактерий

В качестве иллюстрации применения метода, изложенного

разделе 8.3, рассмотрим нециклический транспорт электронов

хроматофорах пурпурных бактерий, который осуществляется со-

гласно следующей

схеме

[Dutton, Prince, 1978; Blankenship, Par-

son, 1979]:

-^CSP^QjSQnA

(8.17)

Здесь С — цитохром: Р — фотохимически активный пигмент ре-

акционного

центра (димер бактериохлорофилла а, Р870);

— соответственно, первичный и вторичный хиноны;

—

псевдомономолекулярные константы скорости, пропорциональ-

ные концентрации экзогенного донора и акцептора соответствен-

но;

— константа скорости, пропорциональная интенсивности

действующего света; k-

, k

, k-

, k

— соответствующие константы

скорости переноса электронов

между

цитохромом и пигментом,

а также

между

и Q

. Предполагается, что все указанные пере-

носчики

входят

единый комплекс. Для простоты рассмотрим

только окислительно-восстановительные реакции переносчиков.

Перенос электронов в реакционном центре, происходящий со-

гласно

схеме

(8.17), может быть описан исходя из графа состоя-

ний

комплекса, представленного на рис. 39 (см. также гл. 3).

0(1) на рисунке означает, что соответствующий переносчик элек-

тронов окислен (восстановлен). Согласно данным, представлен-

ным

гл. 1, для констант скорости справедливы следующие со-

отношения

»£_

^?ft

>£_

~A!,~A:

(8.18)

так как

~10

Уг_

~10\

~10

А:_

~10

— 0,1 —10,

—

0—10

—

0,1—10

с-

Поскольку константы скорости обратных реакций на стадиях

Сч=ьР

QI*±QH

достаточно велики, то циклическими квазисо-

стояниями

первого ранга

будут,

очевидно, только квазисостоя-

ния,

содержащие не более чем два состояния. На рис. 39 для на-

глядности обведены все квазисостояния первого ранга. Новый

размеченный граф квазисостояний примет вид, указанный

на

183

two

«s

К-4

.—•

•s

'«s

1101

s—

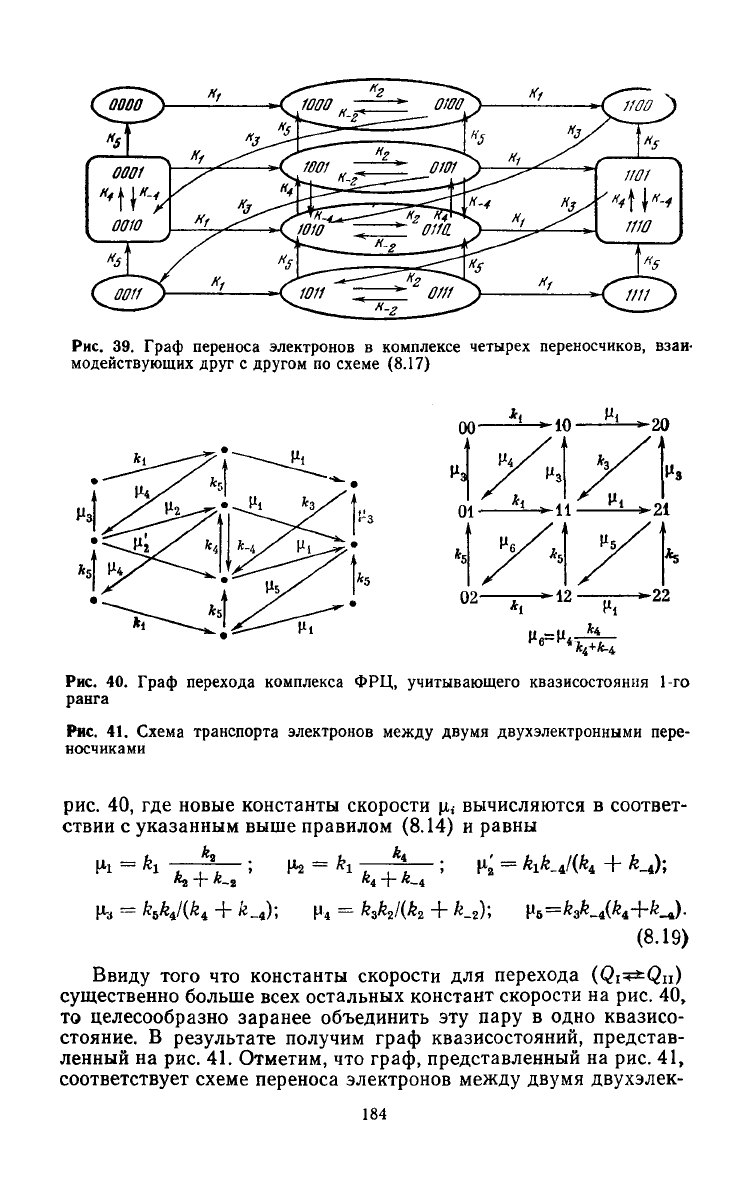
Рис.

39.

Граф переноса электронов

комплексе четырех переносчиков, взаи-

модействующих

друг

другом

по

схеме (8.17)

Рис.

40.

Граф перехода комплекса

ФРЦ,

учитывающего квазисостояния

1-го

ранга

Ряс.

41.

Схема транспорта электронов между двумя двухэлектронными пере-

носчиками

рис.

40, где новые константы скорости ц

(

вычисляются в соответ-

ствии с указанным выше правилом

(8.14)

и равны

+ *-4

(8.19)

= V

Ввиду

того

что

константы скорости

для

перехода

(Qi*)

существенно больше всех остальных констант скорости

на рис. 40,

то целесообразно заранее объединить

эту

пару

одно квазисо-

стояние.

результате получим граф квазисостояний, представ-

ленный

на рис. 41.

Отметим,

что

граф, представленный

на рис. 41,

соответствует схеме переноса электронов

между

двумя двухэлек-

184

тронными переносчиками

, которые взаимодействуют

по

схеме

->•#,->

-*•

(8.20)

Каждый из переносчиков

и R

может находиться

трех

раз-

личных состояниях: 0 — полностью окисленном,

1—частично

восстановленном и 2 — полностью восстановленном.

Фактически граф, представленный на рис. 41, уже достаточ-

но

прост для того, чтобы по нему рассчитать стационарное рас-

пределение вероятностей состояний,

также процесс темнового

восстановления (k, = 0). Так, процесс темнового восстановления

цитохрома

пигмента

могут

быть рассчитаны исходя из

следу-

ющей схемы:

(С°Р°)

(С'Р

)

(&Р

(8.21)

Решая

систему дифференциальных уравнений, соответствующую

этой

схеме

bx—w,

(8.22)

найдем

= х(0) е-

у = J^B-

е-м

+ (у (0)

-*£«°Ц

-^t.

.23)

Следовательно, процесс темнового восстановления цитохрома

пигмента описывается следующим образом:

(С

)

У(О)

*Щ-)е-М,

(8.24)

(8.25)

где х(0), у(0) —стационарные значения вероятностей

{С°Р°)

(СР

рассчитанных исходя

из

графа, представленного

на

рис.

41.

Граф на рис. 41,

следовательно,

решение, полученное

его помощью, очевидно

служат

хорошим приближением для пер-

воначальной схемы рис. 39

времен ~0,01

с.

На меньших вре-

менах, принимая во внимание, что

начальный момент времени

f=0,

комплекс

вероятностью, близкой

единице, находится

состоянии 1100, эволюция комплекса ограничена меньшим чис-

лом состояний и кинетика описывается цепью небольшого числа

последовательных реакций вида

185

8.5.

Сведение

большого

числа

одноэлектронных

переносчиков

меньшему

числу

многоэлектронных

переносчиков

В этом параграфе излагается

метод

упрощения системы диф-

ференциальных уравнений, описывающей перенос электронов в

комплексах молекул переносчиков. Физический смысл

метода

состоит в замене большого числа одноэлектронных переносчи-

ков,

входящих в комплекс, меньшим числом многоэлектронных

переносчиков. Приведенный

метод

является частным

случаем

метода,

изложенного ранее, однако имеет самостоятельное зна-

чение, поскольку укрупнение производится непосредственно на

уровне состояний отдельных переносчиков, а не на уровне со-

стояний

комплекса как целого [Шинкарев, 1978; Венедиктов

др.,

19796].

Рассмотрим перенос электронов в комплексе т одноэлек-

тронных переносчиков С

, ..., С

, происходящий согласно

следующей

схеме:

ft, k

k, k

*m+l

d ^ С

С-

• •

^=+ С

^± .

(8.26)

*-i *-« *-> *-

*-(т+Ц

Здесь k

, k-

• • •,

km, k-m— мономолекулярные константы скоро-

сти переноса электронов в комплексе; k

m+u

(m+1)

—

псев-

домономолекулярные константы скорости, пропорциональные

концентрации

экзогенных доноров и акцепторов в

соответствую-

щей форме.

Пусть кинетические константы скорости k

m+i

, k-

im+li

обмена комплекса со средой существенно меньше, чем констан-

ты скорости переноса электронов внутри комплекса.

Тогда

элек-

трон, попав в такой комплекс, быстро

«размазывается»

по пере-

носчикам,

прежде чем произойдет изменение числа электронов

в комплексе. Следовательно, на временах, больших, чем время,

необходимое для такого усреднения, комплекс переносчиков при-

ближенно можно рассматривать как один т электронный пере-

носчик,

поскольку знания числа электронов, находящихся в дан-

ный

момент в комплексе, достаточно, чтобы найти редокс-состоя-

ния

отдельных переносчиков, входящих в комплекс. Этот много-

электронный переносчик (/?) может переходить из одного со-

стояния

другое

по

следующей

схеме:

Hi HI V-г »т-1 V-m

0^1^:2^t

. .

,l±/n-l^w.

(8.27)

К Я, h, *m-l fc

Цифрами

на этой

схеме

обозначено число электронов, находя-

щееся в комплексе, т. е. восстановленность введенного много-

электронного переносчика, а константы

\1„

X, зависят как от кон-

стант скорости k\, k-i и k

+i, &-

(

m+i) соответственно, так и от ста-

ционарных вероятностей тех состояний, из которых комплекс

переходит

с этими константами скорости. Отметим, что именно

в реакциях с константами скорости ц,„, "К., s = \, ..., т происхо-

дит изменение числа электронов в комплексе.

186

Таким

образом, вместо 2

состояний, соответствующих т од-

ноэлектронным

переносчикам, рассматривается только т+1 со-

стояние,

соответствующее одному m-электронному переносчику.

Система дифференциальных уравнений, отвечающая перехо-

дам этого многоэлектронного переносчика R, содержит только

т+

1 переменное и имеет вид

(8.28)

Хт—

—1

Am-*m,

где Xi—вероятность того, что многоэлектронный переносчик R

имеет / электронов.

Каждому состоянию такого многоэлектронного переносчика

с фиксированным числом электронов соответствует несколько

различных состояний комплекса, отличающихся

друг

от

друга

распределением электронов

между

отдельными переносчиками.

За

время существенно меньшее, чем время, необходимое для из-

менения

числа электронов в комплексе, в такой группе состоя-

ний

с фиксированным числом электронов успевает установиться

равновесие. Поэтому для определения новых констант скорости

переходов ц,„ А, для схемы

(8.27)

можно рассмотреть равнове-

сие в следующей системе т одноэлектронных переносчиков

..., С

, содержащей ровно s электронов и взаимодействую-

щих по

схеме

С^С

^---^

(8.29)

Обозначим через

P(C

) вероятность того, что в комплексе

переносчиков

с фиксированным числом электронов (s) и взаи-

модействующих

друг

другом

согласно

схеме

(8.29), С,-й пере-

носчик

находится в восстановленном состоянии. Тогда новые

константы

скорости ц, и К, для схемы

(8.27)

могут

быть найде-

ны

согласно следующим формулам:

k_,P

(Cl.,)

m+1

(Ci,,,).

(8.30)

Стационарные

вероятности

P(C?

P(Ci

P (Cm

P(C

mtS

)

мож-

но

найти из следующей системы уравнений, получающейся при-

менением

принципа детального равновесия к

схеме

(8.29):

(Clcl)

= Р

(С;с

)

(8.31)

187

где l\t = соответствующие константы равновесия, а

-i

Р(С

{

С°)

есть стационарная вероятность того, что Сгй перенос-

чик

электронов восстановлен, а С

й окислен.

Каждое из уравнений этой системы эквивалентно на самом

/т — 2\ (т —2)!

деле

= - уравнениям относительно ста-

s — 1 / (m

—s—l)!(s—1)!

ционарных вероятностей состояний комплекса как целого. На-

пример,

первое уравнение системы

(8.31)

эквивалентно

следую-

1т — 2\

щей системе уравнении:

\s—1 1

(delete),

...

)

= Р

{ciclcic),...

с)).

(8.32)

Здесь i

означает номер переносчиков, которые восстановлены, а

события

(C\ClC)jO),

... Cj

) означают, что первый, i

, h, ..., i

переносчики восстановлены, а остальные (т—s) окислены.

Рассмотрим произвольное состояние комплекса с s электро-

нами

(t'i, i

, ..., i.), где, как и ранее, i

указывает переносчик, на

котором находится й-й электрон. Для того чтобы комплекс из

состояния (1, 2, ..., s) перешел в состояние (»',, £

, ..., i.), нужно,

чтобы s-й электрон перешел на i,-e место, ..., 1-й электрон пе-

решел на i

e место. Учитывая справедливость принципа деталь-

ного равновесия для схемы

(8.29)

и также то, что каждому пере-

ходу

электрона соответствует определенная константа равнове-

сия,

а последовательно осуществляемым переходам—произве-

дение соответствующих констант равновесия, имеем

Pi,!,

={Ks+i-Ks+2---K(

)(K

-K

i---Ki

)

•

••••

(К

••••Kt

Или,

что то же,

«>

(8.33)

1 •• i

Г=1

Подставляя полученные выражения для вероятностей состояний

комплекса в условие нормировки ZJPI ~

< получим

Рх

»...*=

(8.34)

Откуда с

учетом

(8.33)

несложно найти выражение для произ-

вольной вероятности

/?w,...j

а следовательно, и выражение для

вероятностей редокс-состояний отдельных переносчиков, входя-

188

щих в комплекс, просуммировав вероятности тех состояний ком-

плекса с фиксированным числом электронов, в которых рассмат-

риваемый переносчик находится в интересующем нас состоянии.

Таким образом, системы уравнений (8.31), вместе с условием'

нормировки для стационарных вероятностей состояний комплек-

са с фиксированным числом электронов, достаточны для нахож-

дения

Для вычисления новых констант скорости ц„ К, в

схеме

(8.27)

необходимо, согласно формуле (8.30), стационарные ве-

роятности умножить на те константы скорости, которые приво-

дят к изменению числа электронов в комплексе.

Так,

например, для случая, когда в комплексе находится

только один электрон

(s=l),

имеем

следующую

схему

перехо-

дов

между

состояниями комплекса:

(10

... 0) ^Ь (010 ... 0) §1

• • •

:£ (0 ... 01). (8.35)

В данном

случае

отдельные состояния комплекса можно отож-

дествить с восстановленными формами соответствующих пере-

носчиков.

Решая систему уравнений

(8.31)

для схемы (8.35), на-

ходим

Р(С\

)

= ! ; Р (С) г) =^

1+P

P++P

•

где

-..

.•/(,,

Следовательно,

\-?

константы скорости щ и Я,, равны

1 +

P3-I

= k.

1+P*+Ps-|

Если стадии переноса электрона внутри комплекса практи-

чески необратимы (&_

=&_j=... = &_

=0), то возможны только

следующие состояния комплекса: 0 ... 01, 0 ... 011, 0 ... 0111, ...

•

•, 01... 1, 1... 1, относительная вероятность которых в группе

состояний с фиксированным числом электронов близка к едини-

це.

Ввиду

необратимости, а также того, что всю группу с фикси-

189

рованным числом электронов представляет только одно состоя-

ние,

параметры ц„ X, равны соответственно й, и

m+l

В этом

случае

схема переходов

(8.27)

примет особенно простой вид

ft, ft,

А,

t t

••

-Z(m —

l)^z—m.

(8.36)

Очевидно, что приведенный в этом параграфе метод упрощен-

ного рассмотрения переноса электронов справедлив на временах,

больших, чем время, необходимое для «размазывания» электро-

на

по комплексу, и тем более точен, чем больше отличаются по

порядку величины констант скорости переноса электрона внут-

ри

комплекса от констант скорости обмена комплекса со средой.

Ясно также, что он может быть применен к произвольной

схеме

взаимодействия переносчиков, а не только к линейной, как в

рассмотренном случае. Если для переноса электронов в комплек-

се, состоящем из большого числа переносчиков, имеется иерар-

хия в величинах констант скорости переноса электронов

между

ними,

то, последовательно применяя указанный метод укрупне-

ния

к группе рядом расположенных переносчиков, константы

скорости у которых существенно больше, чем константы скорости

обмена электронами

между

группами, можно свести описание

функционирования

такого комплекса к переносу электронов

между

меньшим числом многоэлектронных переносчиков (на

временах, больших, чем время, необходимое для усреднения

электронов

между

переносчиками такой группы).

Заключение

В данной главе мы рассмотрели методы упрощенного описа-

ния

переноса электронов в комплексах. При этом были использо-

ваны два подхода для анализа такого рода систем.

В первом — предполагается, что комплекс переносчиков элек-

тронов уже исходно устроен так, что в нем реализуется опреде-

ленная

иерархия величин констант скорости. В этом

случае

для

описания

кинетики переноса электронов необходимо использо-

вать различные стандартные методы исследования систем диф-

ференциальных уравнений с малым параметром. Дополнитель-

ные возможности для упрощения

дает

то обстоятельство, что ин-

тересующие нас состояния отдельных переносчиков представля-

ют собой

сумму

состояний комплекса. Поэтому во многих слу-

чаях можно пренебречь большей частью слагаемых этой суммы

ввиду их малости. В качестве примера такого рода подхода мож-

но

привести анализ кинетического поведения ФРЦ пурпурных

бактерий (см. подробнее гл. 9). В реакционном центре уже из-

начально имеется определенная иерархия величин констант ско-

рости переноса электронов

между

отдельными переносчиками.

Эта иерархия приводит к

тому,

что для описания переноса элек-

тронов на временах, сопоставимых с частотой попадания воз-

190