Salby M.L. Fundamentals of Atmospheric Physics

Подождите немного. Документ загружается.

430 14 Atmospheric Waves

These features allow the wave field to be constructed from a superposition of

plane waves, which is expressed in the Fourier integral

p'(x, t) - (21r)3 f f f P~l(z)ei(kx+ly-~t' dkdld~r

l fff

: (2,n.) 3 ~

Pff(z)e i(k'x-crt) dkdcr,

(14.11.1)

wherein the z dependence must satisfy boundary conditions. Equation

(14.11.1) describes a spectrum of monochromatic plane waves, individ-

ual components of which have angular frequency or, wavenumber vector

k = (k,l),

and complex amplitudes

P~(z)

that contain the magnitude

and phase of oscillations. An individual component of the wave spectrum

(Fig. 14.2) has lines of constant phase:

kx + ly-

at = const, which propagate

Cy T, Ikl

! ! I

.,,.... ...... . ....."

c=~

2~; " ~ .... ~. x

k -"

Figure 14.2 An individual plane wave component having wavenumber vector k = (k, l) and

frequency tr. Lines of constant phase:

kx + ly-

trt - const, propagate parallel to k (tr > 0) or

antiparallel to k (tr < 0), with

phase speed c = tr/[k[.

Phase propagation in the x and y directions

is described by the

trace speeds Cx = tr/k

and

Cy = o/l,

which equal or exceed c and are related to

it through

1/c 2 + 1/c 2

1/C 2,

SO they do not represent its components. As k becomes orthogonal

to a direction, the trace speed in that direction becomes infinite.

14.1 Description of Wave Propagation

431

in the direction of k with the

phase speed

c = ik I , (14.11.2)

where

Ikl 2

= k 2 + l 2. Phase propagation in the x and y directions is described

by the

trace speeds

Cx= k'

or (14.11.3)

Cy = -{ .

2 2 r

Note that

c x + Cy ~

According to Fig. 14.2, the trace speed in a given

direction equals or exceeds the phase speed and approaches infinity as k

becomes orthogonal to that direction.

By the Fourier integral theorem (see, e.g., Rektorys, 1969), the complex

amplitudes in (14.11.1) follow as

fff

Pk~(z) -- p'(x, y,

z, t)e -i(kx+ly-~rt)

dxdydt,

(14.12.1)

which defines the

Fourier transform

of the variable p' at level z. Equation

(14.12.1) describes a spectrum of complex wave amplitude over the space-

time scales k, l, and o-. Real p' requires the amplitude spectrum to satisfy the

Hermitian property

-~ - P~* (14.12.2)

P-~-t ~t 9

Because (14.11.1) and (14.12.1) constitute a one-to-one mapping,

p'(x, t)

in physical space and its counterpart in Fourier space,

P~(z),

are equivalent

representations of the wave field. The

power spectrum, IP~I

12, then describes the

distribution over wavenumber and frequency of variance [p,[2, which reflects

the energy in the wave field. In general, a disturbance excites a continuum of

space and timescales, so wave variance follows as an integral over wavenumber

and frequency:

1 ~ 12

f f

Ip'(x,

t)12dxdt-(2,rr) 3

f f f=

IP~ dkdcr,

(14.13)

which is known as

Parseval's theorem.

Differentiating p' in physical space is equivalent to multiplying its transform

P~t by the corresponding space and time scales:

ap'

ikP~,

•p!

ilP~z,

(14.14)

ap,

+-~ -i~rP~t ,

the demonstration of which is left as an exercise. Then applying (14.12.1)

432 14

Atmospheric Waves

transforms the material derivative into

Dp'

--+ --iwPk~l,

(14.15.1)

where

to - o- kK (14.15.2)

is the

intrinsic frequencymthat

relative to the medium, for the component with

frequency ~r and zonal wavenumber k. The term -kK represents a Doppler

shift of the intrinsic frequency by background motion. A component propa-

gating opposite to ~ is Doppler-shifted to higher intrinsic frequency: w > ~r,

whereas one propagating in the same direction as K is Doppler-shifted to lower

intrinsic frequency: o~ < or.

Applying (14.12.1) transforms the governing equations in physical space:

(14.6), (14.9.2), and (14.10), into their counterparts in Fourier space:

32Pfft

Ikl2e~

= 0, (14.16.1)

~Z 2

aPk

= 0 z = O, (14.16.2)

OPk~l to 2

Pk5 -- 0 Z = H.

(14.16.3)

3z g

Space-time dependence involving derivatives with respect to x, y, and t has

been reduced to algebraic dependence on the scales k, l, and o- for individ-

ual modes, which can be resynthesized via (14.11.1). The general solution of

(14.16.1) satisfying the lower boundary condition (14.16.2) is of the form

Pfft(z) = Z

cosh(Iklz) (14.17)

(Fig. 14.1). Substituting into the upper boundary condition (14.16.3) then

yields the algebraic identity

o~ 2 - glkl

tanh(Ikln). (14.18)

Referred to as the

dispersion relation,

(14.18) must be satisfied by each com-

ponent

(k,l,~r)

if the wave spectrum is to obey the goveming equations. The

dispersion relation expresses one of the space-time scales (e.g., frequency)

in terms of the others. Therefore, the spatial scales of an individual wave

component determine its frequency.

14.1.3 Limiting Behavior

According to (14.18), different horizontal scales propagate relative to the

medium with different intrinsic phase speeds

Ikl

[gHtanh(Ikl

~ ] '

(14.19)

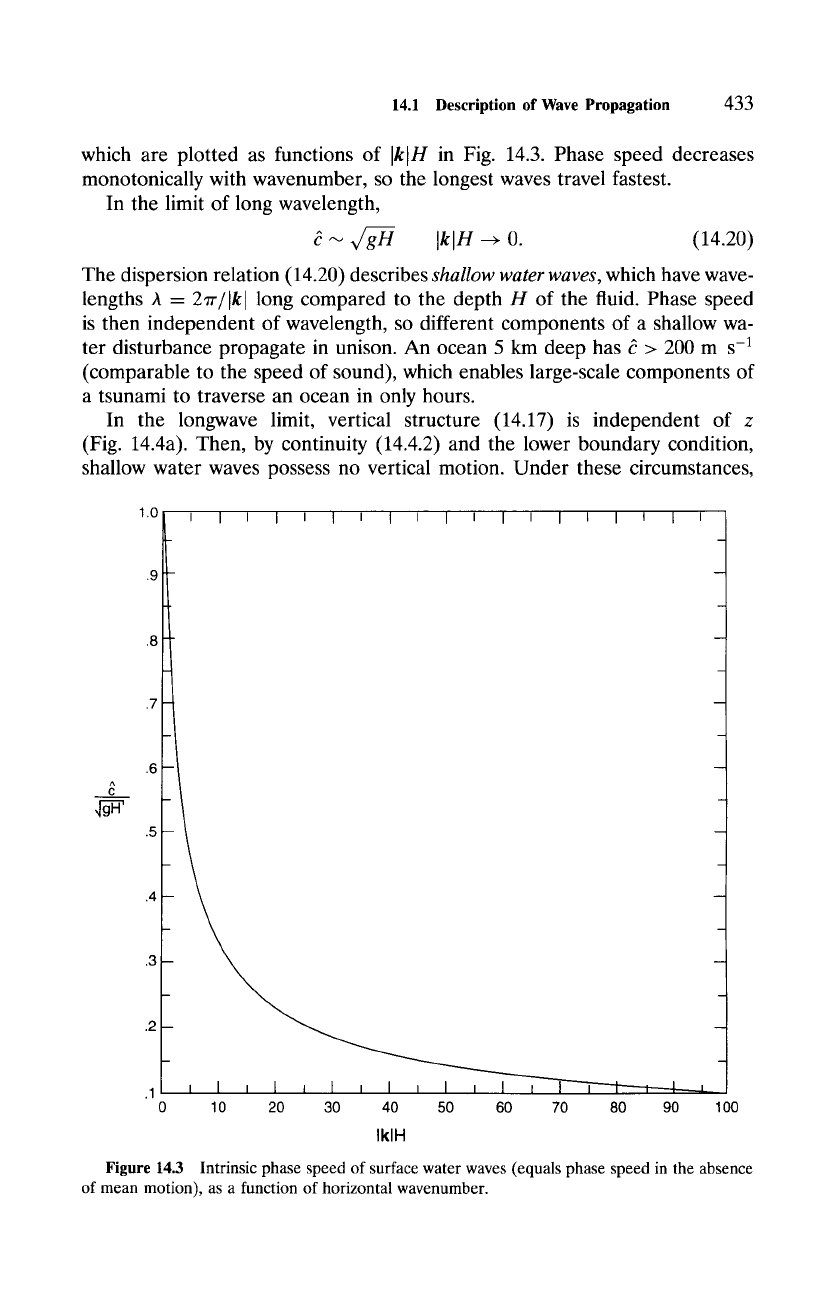
14.1

Description of Wave Propagation

433

which are plotted as functions of IklH in Fig. 14.3. Phase speed decreases

monotonically with wavenumber, so the longest waves travel fastest.

In the limit of long wavelength,

~ ~ Ikln --+ O. (14.20)

The dispersion relation (14.20) describes shallow water waves, which have wave-

lengths A = 2~r/Ikl long compared to the depth H of the fluid. Phase speed

is then independent of wavelength, so different components of a shallow wa-

ter disturbance propagate in unison. An ocean 5 km deep has ~ > 200 m s -1

(comparable to the speed of sound), which enables large-scale components of

a tsunami to traverse an ocean in only hours.

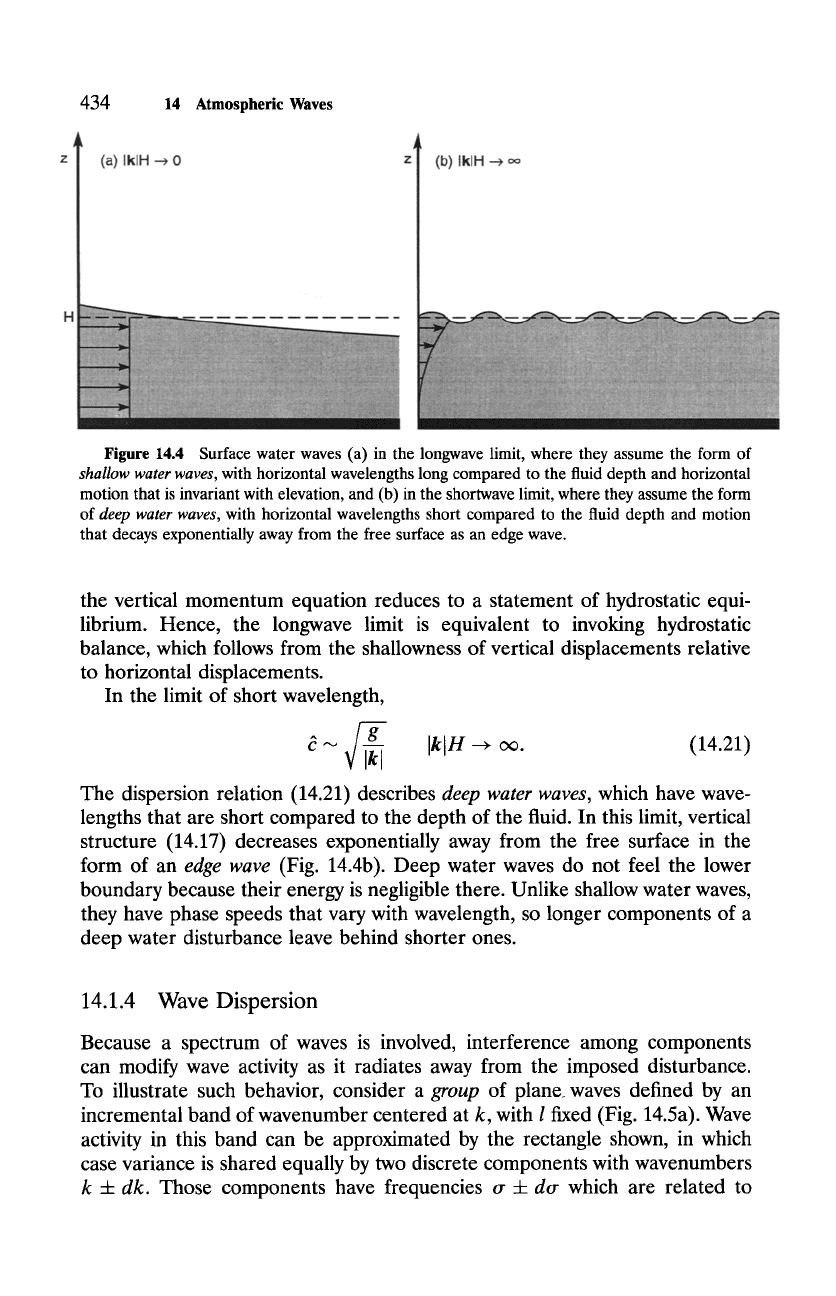
In the longwave limit, vertical structure (14.17) is independent of z

(Fig. 14.4a). Then, by continuity (14.4.2) and the lower boundary condition,

shallow water waves possess no vertical motion. Under these circumstances,

1.0

I I I I I I I I I I I I I I I I I I

0 10 20 30 40 50 60 70 80 90 100

IkIH

Figure 14.3 Intrinsic phase speed of surface water waves (equals phase speed in the absence

of mean motion), as a function of horizontal wavenumber.

434

Atmospheric Waves

(a) IklH ---> 0

(b) IklH ---> oo

Figure 14.4 Surface water waves (a) in the longwave limit, where they assume the form of

shallow water waves, with horizontal wavelengths long compared to the fluid depth and horizontal

motion that is invariant with elevation, and (b) in the shortwave limit, where they assume the form

deep water waves, with horizontal wavelengths short compared to the fluid depth and motion

that decays exponentially away from the free surface as an edge wave.

the vertical momentum equation reduces to a statement of hydrostatic equi-

librium. Hence, the longwave limit is equivalent to invoking hydrostatic

balance, which follows from the shallowness of vertical displacements relative

to horizontal displacements.

In the limit of short wavelength,

~ ~~kl Ik[H--> oo.

(14.21)

The dispersion relation (14.21) describes

deep water waves,

which have wave-

lengths that are short compared to the depth of the fluid. In this limit, vertical

structure (14.17) decreases exponentially away from the free surface in the

form of an

edge wave

(Fig. 14.4b). Deep water waves do not feel the lower

boundary because their energy is negligible there. Unlike shallow water waves,

they have phase speeds that vary with wavelength, so longer components of a

deep water disturbance leave behind shorter ones.

14.1.4 Wave Dispersion

Because a spectrum of waves is involved, interference among components

can modify wave activity as it radiates away from the imposed disturbance.

To illustrate such behavior, consider a

group

of plane, waves defined by an

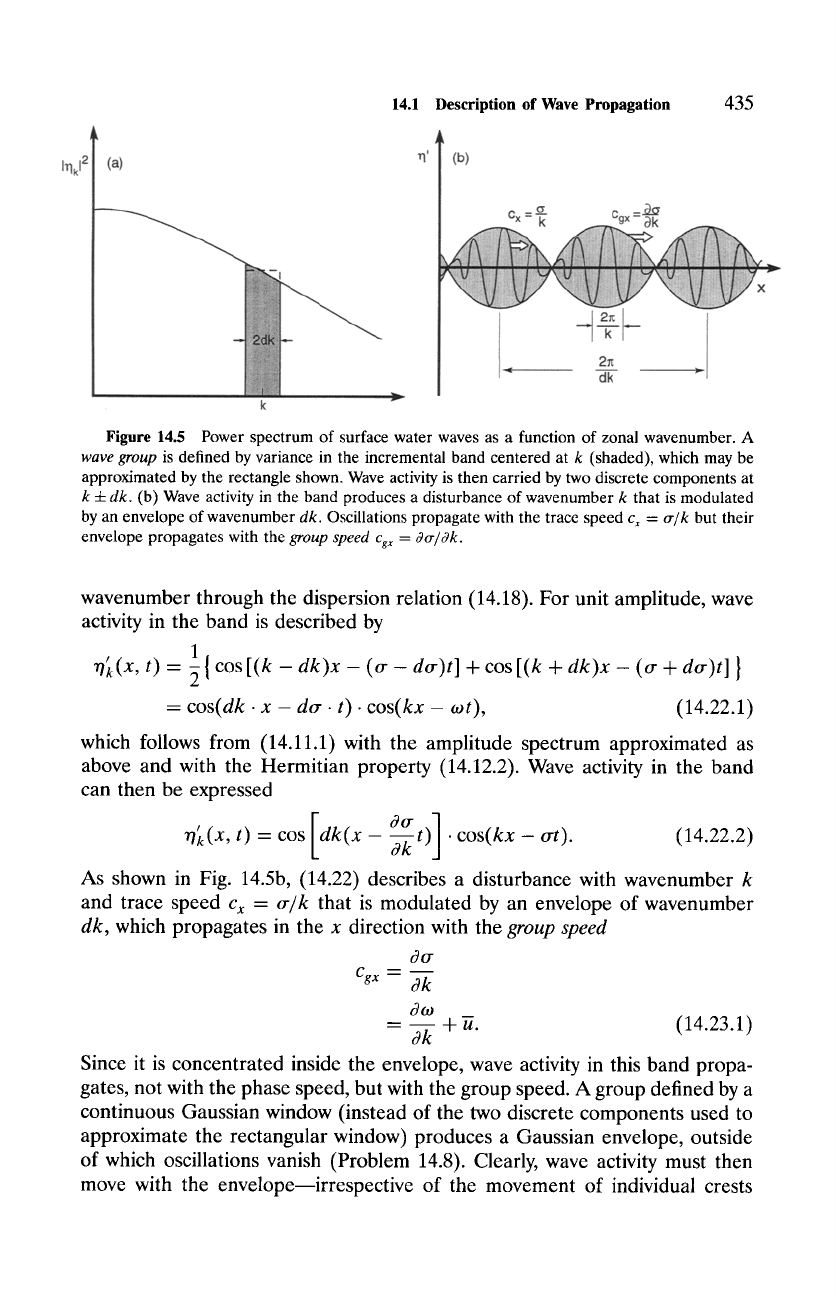
incremental band of wavenumber centered at k, with I fixed (Fig. 14.5a). Wave

activity in this band can be approximated by the rectangle shown, in which

case variance is shared equally by two discrete components with wavenumbers

k + dk.

Those components have frequencies tr + dtr which are related to

I'rlk 12

14.1 Description of Wave Propagation

435

(a)

(b)

c -_0_~

. __ gx- ~k

V -

q h-

Figure 14.5 Power spectrum of surface water waves as a function of zonal wavenumber. A

wave group

is defined by variance in the incremental band centered at k (shaded), which may be

approximated by the rectangle shown. Wave activity is then carried by two discrete components at

k -4-dk.

(b) Wave activity in the band produces a disturbance of wavenumber k that is modulated

by an envelope of wavenumber

dk.

Oscillations propagate with the trace speed

c x = tr/k

but their

envelope propagates with the

group speed Cgx = ~tr/,3k.

wavenumber through the dispersion relation (14.18). For unit amplitude, wave

activity in the band is described by

, 1

wk(x, t) - ~{ cos [(~ -

dk)x - (,~ - d~)t] +

cos [(~ +

d~:)x - (~ + d~)t] }

- cos(dk 9 x - do-. t). cos(kx - tot), (14.22.1)

which follows from (14.11.1) with the amplitude spectrum approximated as

above and with the Hermitian property (14.12.2). Wave activity in the band

can then be expressed

r/~(x, t) -- cos

dk(x - -~t) 9

cos(kx - o-t). (14.22.2)

As shown in Fig. 14.5b, (14.22) describes a disturbance with wavenumber k

and trace speed

Cx = o-/k

that is modulated by an envelope of wavenumber

dk,

which propagates in the x direction with the

group speed

3o-

Cgx = 3k

3to

= ~k + u. (14.23.1)

Since it is concentrated inside the envelope, wave activity in this band propa-

gates, not with the phase speed, but with the group speed. A group defined by a

continuous Gaussian window (instead of the two discrete components used to

approximate the rectangular window) produces a Gaussian envelope, outside

of which oscillations vanish (Problem 14.8). Clearly, wave activity must then

move with the envelope~irrespective of the movement of individual crests

436

Atmospheric Waves

and troughs inside it. A similar analysis applied to wavenumber I with k fixed

yields the group speed in the y direction:

30"

Cgy = 31

3to

= ---/. (14.23.2)

Then wave activity is propagated in the

x-y

plane with the

group velocity

30" 30")

Ok'31

oo)

= .

(14.23.3)

A function of k and l,

describes the propagation of wave activity in indi-

vidual bands of the spectrum (14.11.1). According to (14.23.3), background

motion advects wave activity with the basic flow. The intrinsic group velocity

~:g - Cg - -~i

(14.23.4)

gives the same information relative to the medium and is recognized as just

the gradient of to with respect to k = (k, l).

Let us return now to the limiting forms of surface water waves described

previously and in the absence of background motion: K = 0. In the longwave

limit, phase speed (14.20) is independent of k. Since individual wave compo-

nents all propagate with the same speed, a disturbance comprised of shallow

water waves retains its initial shape. Such waves are said to be

nondispersive

because a disturbance that is initially compact remains so. The group speed

of shallow water waves follows from (14.23) as

Cg = x/gH

= c. (14.24)

Because all of its components propagate with identical phase speed, a group

of shallow water waves centered at wavenumber k propagates in the same

direction and with the same speed.

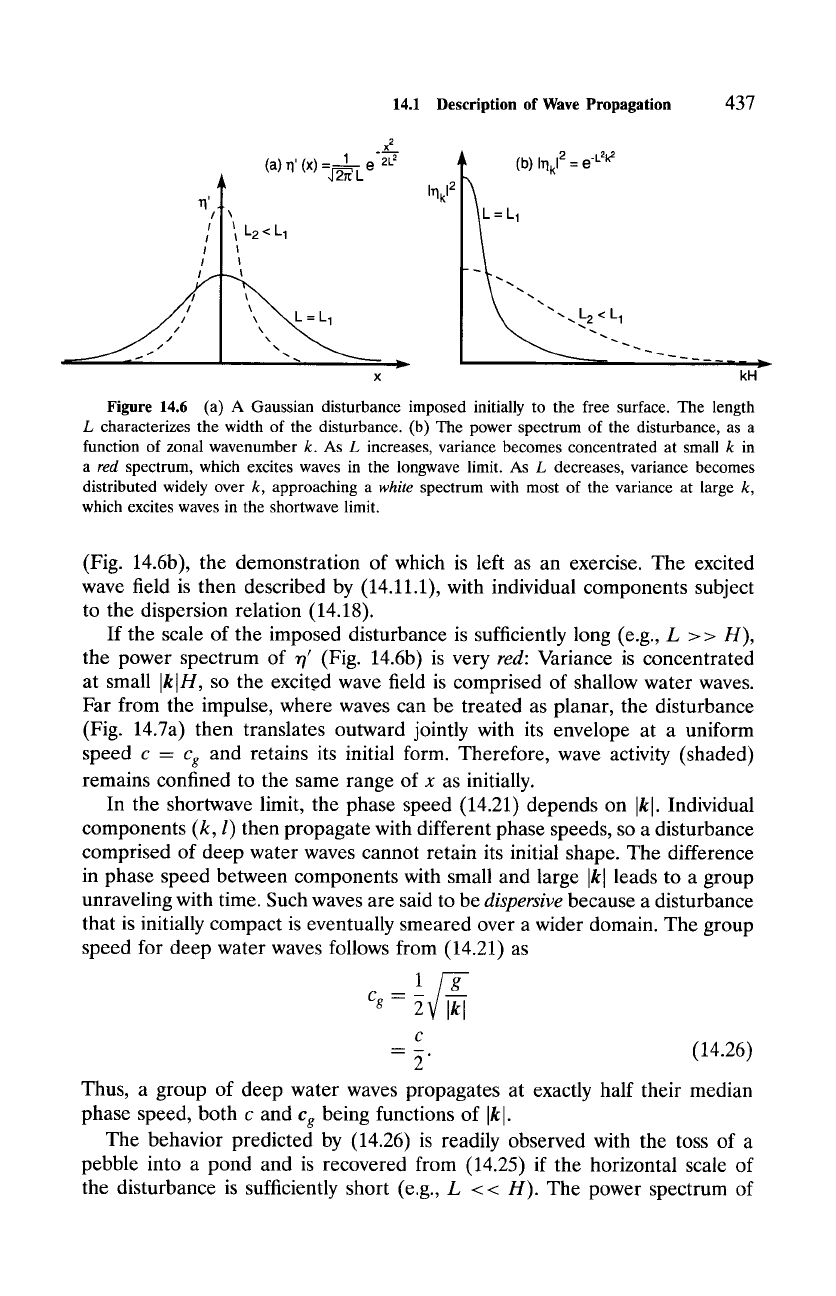
An example is presented in Figs. 14.6 and 14.7. The free surface is initialized

with a compact disturbance (Fig. 14.6a)

x 2 +y2

r/'(x, y, 0) = ~_~------~e 2L-z , (14.25.1)

with characteristic horizontal scale L. Because it is not simple harmonic, that

disturbance excites a continuum of waves. Transforming (14.25.1) via (14.12.1)

with t = 0 gives its power spectrum

[ r/k/I 2=

e -L2(k2+12)

(14.25.2)

14.1

Description of Wave Propagation

437

x 2

1 2L 2

(a) q' (x)-~---L e

~','I \', L2<L I

/1i

/l '~~L

L 1

Irlk 12

(b) Irlk 12 = e "L2k2

...

L1 ~

Figure 14.6

(a) A Gaussian disturbance imposed initially to the free surface. The length

L characterizes the width of the disturbance. (b) The power spectrum of the disturbance, as a

function of zonal wavenumber k. As L increases, variance becomes concentrated at small k in

a red

spectrum, which excites waves in the longwave limit. As L decreases, variance becomes

distributed widely over k, approaching a

white

spectrum with most of the variance at large k,

which excites waves in the shortwave limit.

(Fig. 14.6b), the demonstration of which is left as an exercise. The excited

wave field is then described by (14.11.1), with individual components subject

to the dispersion relation (14.18).

If the scale of the imposed disturbance is sufficiently long (e.g., L > > H),

the power spectrum of r/' (Fig. 14.6b) is very

red:

Variance is concentrated

at small

IklH,

so the excit.ed wave field is comprised of shallow water waves.

Far from the impulse, where waves can be treated as planar, the disturbance

(Fig. 14.7a) then translates outward jointly with its envelope at a uniform

speed c = c~ and retains its initial form. Therefore, wave activity (shaded)

remains confined to the same range of x as initially.

In the shortwave limit, the phase speed (14.21) depends on

Ikl.

Individual

components (k, l) then propagate with different phase speeds, so a disturbance

comprised of deep water waves cannot retain its initial shape. The difference

in phase speed between components with small and large

Ikl

leads to a group

unraveling with time. Such waves are said to be

dispersive

because a disturbance

that is initially compact is eventually smeared over a wider domain. The group

speed for deep water waves follows from (14.21) as

cg-~ Ikl

-- ~. (14.26)

Thus, a group of deep water waves propagates at exactly half their median

phase speed, both c and

being functions of

Ikl.

The behavior predicted by (14.26) is readily observed with the toss of a

pebble into a pond and is recovered from (14.25) if the horizontal scale of

the disturbance is sufficiently short (e.g., L < < H). The power spectrum of

438

14 Atmospheric Waves

Cg=C

Cg= ~.

(a) L >> H

Ikl

L H

(b) <<

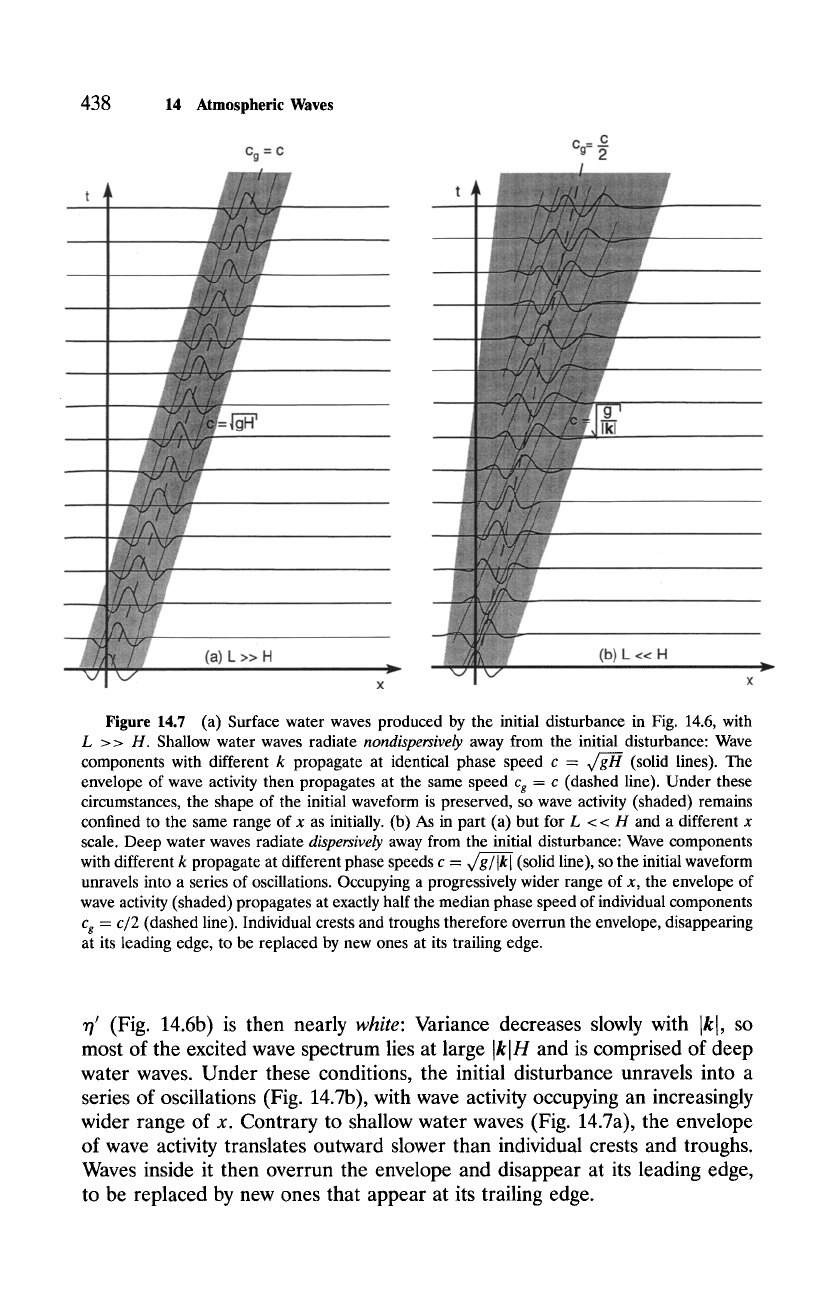
Figure 14.7 (a) Surface water waves produced by the initial disturbance in Fig. 14.6, with

L > > H. Shallow water waves radiate

nondispersively

away from the initial disturbance: Wave

components with different k propagate at identical phase speed c = ~ (solid lines). The

envelope of wave activity then propagates at the same speed c 8 = c (dashed line). Under these

circumstances, the shape of the initial waveform is preserved, so wave activity (shaded) remains

confined to the same range of x as initially. (b) As in part (a) but for L < < H and a different x

scale. Deep water waves radiate

dispersively

away from the initial disturbance: Wave components

with different k propagate at different phase speeds c = ~ (solid line), so the initial waveform

unravels into a series of oscillations. Occupying a progressively wider range of x, the envelope of

wave activity (shaded) propagates at exactly half the median phase speed of individual components

cg = c/2

(dashed line). Individual crests and troughs therefore overrun the envelope, disappearing

at its leading edge, to be replaced by new ones at its trailing edge.

r/' (Fig. 14.6b) is then nearly

white:

Variance decreases slowly with [kl, so

most of the excited wave spectrum lies at large

IklH

and is comprised of deep

water waves. Under these conditions, the initial disturbance unravels into a

series of oscillations (Fig. 14.7b), with wave activity occupying an increasingly

wider range of x. Contrary to shallow water waves (Fig. 14.7a), the envelope

of wave activity translates outward slower than individual crests and troughs.

Waves inside it then overrun the envelope and disappear at its leading edge,

to be replaced by new ones that appear at its trailing edge.

14.2 Acoustic Waves 439

14.2 Acoustic Waves

The simplest wave motions supported by the governing equations are sound

waves. Compressibility provides the restoring force for simple acoustic waves,

which have timescales short enough to ignore rotation, heat transfer, fric-

tion, and buoyancy. Further, because they are longitudinal disturbances, in

which fluid displacements are parallel to the propagation vector k, we may

consider motion in the x direction. Under these circumstances, air motion is

governed by

du 1 ~p

= (14.27.1)

dt p dx

dp l- p-- - 0 (14.27.2)

dt dx

pp-~ conserved, (14.27.3)

where Poisson's relation (2.30) serves as a statement of the first law under adi-

abatic conditions. Applying the logarithm to (14.27.3) followed by the material

derivative obtains

1 dlnp ldp

3' dt p dr'

which, on substitution into (14.27.2), yields

1 dlnp du

t -- 0. (14.28)

3" dt dx

For a homogeneous basic state (e.g., one that is isothermal and in uniform

motion), the first-order perturbation equations are then

Du' 1 ~p'

Dt -fi dx

Dp' Ou'

YP~

Dt 3x

-0.

(14.29)

These may be consolidated into a single second-order equation

D2p ' _d2p '

Dt 2 TRT ~ - O. (14.30)

Equation (14.30) is a one-dimensional wave equation for the perturbation

pressure p', from which other field properties follow. Its coefficients are inde-

pendent of x and t, so we may consider solutions of the form exp[i(kx- r

which is an implicit application of (14.12.1). Substituting then transforms

(14.30) into the dispersion relation

~2 = 7RT, (14.31)