Salby M.L. Fundamentals of Atmospheric Physics

Подождите немного. Документ загружается.

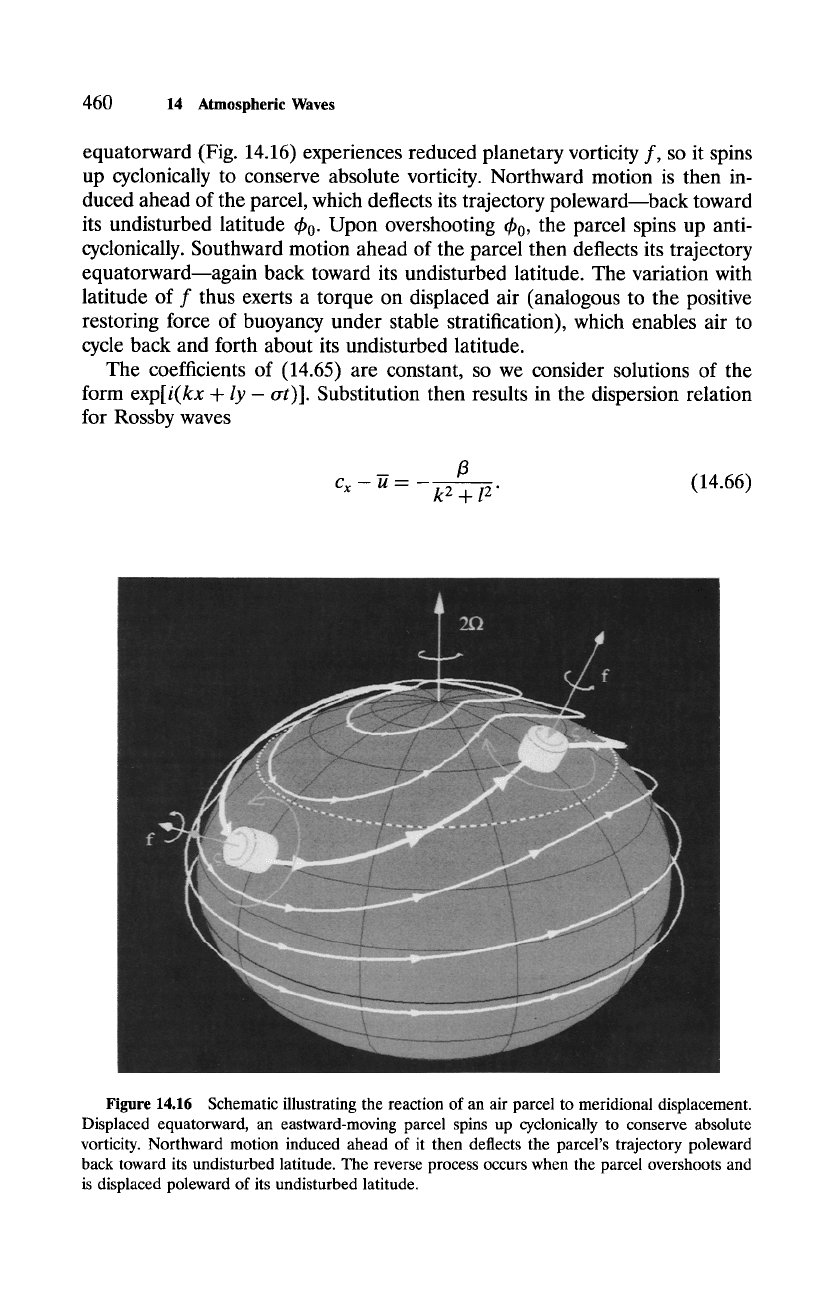
460 14 Atmospheric Waves

equatorward (Fig. 14.16) experiences reduced planetary vorticity f, so it spins

up cyclonically to conserve absolute vorticity. Northward motion is then in-

duced ahead of the parcel, which deflects its trajectory polewardmback toward

its undisturbed latitude ~b 0. Upon overshooting ~b 0, the parcel spins up anti-

cyclonically. Southward motion ahead of the parcel then deflects its trajectory

equatorwardmagain back toward its undisturbed latitude. The variation with

latitude of f thus exerts a torque on displaced air (analogous to the positive

restoring force of buoyancy under stable stratification), which enables air to

cycle back and forth about its undisturbed latitude.

The coefficients of (14.65) are constant, so we consider solutions of the

form

exp[i(kx + ly-

trt)]. Substitution then results in the dispersion relation

for Rossby waves

Cx - ~ - - k2 + ~ 9 (14.66)

Figure 14.16 Schematic illustrating the reaction of an air parcel to meridional displacement.

Displaced equatorward, an eastward-moving parcel spins up cyclonically to conserve absolute

vorticity. Northward motion induced ahead of it then deflects the parcel's trajectory poleward

back toward its undisturbed latitude. The reverse process occurs when the parcel overshoots and

is displaced poleward of its undisturbed latitude.

14.5 Rossby Waves 461

Relative to the basic state, Rossby waves propagate only westward. 4 Their

intrinsic trace speed,

c x --~ = w/k,

is proportional to the local gradient of

planetary vorticity and inversely proportional to the horizontal wavenumber

squared. Hence, Rossby waves are dispersive, with the gravest dimensions

propagating westward fastest. Small scales with slow phase speeds will be

swept eastward by westerly zonal flow, as is typical of synoptic disturbances

(Fig. 1.9). Stationary Rossby waves forced orographically propagate only if the

basic flow is westerly.

The intrinsic frequency I~oh of Rossby waves is proportional to/3, so it has

a high-frequency cutoff of 21)--analogous to the cutoff N for internal gravity

waves.

The solenoidal character of Rossby waves distinguishes them from gravity

waves, which are nearly irrotational. Because Rossby waves are almost non-

divergent, the Helmholtz theorem (12.4) implies that horizontal motion can

be characterized by the vorticity field, with vertical motion ignored to a first

approximation. Conversely, gravity waves are determined chiefly by vertical

motion and hence by the divergence field. Although the essential properties

of Rossby waves follow from the rotational component of motion, divergence

enters by forcing absolute vorticity.

14.5.2 Rossby Wave Propagation in Three Dimensions

To examine three-dimensional wave propagation, divergence must be ac-

counted for. Within the framework of quasi-geostrophy, air motion is

governed by conservation of quasi-geostrophic potential vorticity. Lineariz-

ing (12.49) about an isothermal basic state in uniform motion leads to the

perturbation potential vorticity equation for wave motion on a beta plane

D [V2~O,+{f2~ 10 [_Oq/)]

0q/=0 ' (14.67)

D t \ N 2 ] p -~z ~ P -~z + fl 3 x

where z refers to log-pressure height and q/ = (1/f0)~' to the geostrophic

streamfunction.

Since coefficients are again constant, we consider solutions of the form

exp[(z/2H)+ i(kx + ly+ mz-crt)].

Substitution into (14.67) recovers the

dispersion relation for

quasi-geostrophic Rossby waves

~ ,

{f~'~

1 (14.68)

C x -- U -- k 2 n t- l 2 n t-

IkN2,]

( m2 + 4-H -~)

4The

direction of Rossby wave propagation can be deduced from the vorticity pattern in Fig.

14.16, relative to the frame of the material contour shown. Southward motion behind the cyclonic

anomaly displaces that segment of the material contour equatorward, shifting the wave trough west-

ward. Northward motion behind the anticyclonic anomaly has the same effect on the wave crest.

462 14 Atmospheric Waves

If the denominator is identified as the effective total wavenumber squared,

(14.68) has a form analogous to (14.66), but modified by the stratification of

mass. For many applications, m 2 > > 1/4H 2. Vertical stretching (12.36) is then

embodied in the term

(f2/N2)m2.

As the vertical wavelength

2,rr/m --+ oo,

divergence forcing of vorticity vanishes and (14.68) reduces to.the dispersion

relation for barotropic nondivergent Rossby waves.

Because their intrinsic phase speeds depend on wavenumber, Rossby waves

are dispersive. Expressing (14.68) as

/3k

(.o -- -- [" f2"~

(14.69)

k2-1-12-1- ~k ) "~g

(m2+ a-B:)

leads to the components of group velocity:

k2 __ 12. { f2"~ 1

-- -- ~'N2 J (m2 + 4-H-T)

{f2'~

o(2%k)

Cg x

--U- /~1- 12 = k

1+ ~ , (14.70.1)

[

k2 + 12 + kui] (m2 + ~-r)

]

213kl

2&o a

Cgy

= [ /'f2'~ 1

]2"-- /3k' (14.70.2)

9 k2 -+- 12 + \N2] ( m2 + ~-H--g)

2em (6) t'

1 2 "

cg z

[ k2+ 12-1 - (Nf--4~ ( m2+ TH-r)] ~N2 ] ~ (14.70.3)

Wave activity propagates in the positive y and z directions if

> 0 and

> 0, respectively. Since ~o < 0, the form adopted for q,' then implies

phase propagation in the opposite directions. Thus, downward and equator-

ward phase propagation corresponds to energy propagation that is upward and

poleward. For stationary waves in the presence of westerly flow, these condi-

tions translate into phase surfaces that tilt westward in the direction of energy

propagation, for example, in the upward and equatorward directions for the

circumstances just described (Fig. 14.17).

Contrary to

Cgy

and

Cgz,

the sign of

Cg x --U

depends on the magnitude of

k. For k < & (e.g., long zonal wavelength), group propagation relative to the

t~ n

medium is westward. But k > ~-~ (e.g., short zonal wavele gth) gives intrinsic

z~lOJ I

group propagation that is eastward. Separating westward and eastward group

propagation is the locus of wavenumbers that makes

Cgx - -5

vanish:

ke-le+\Ne

(me+~H2).

(14.71)

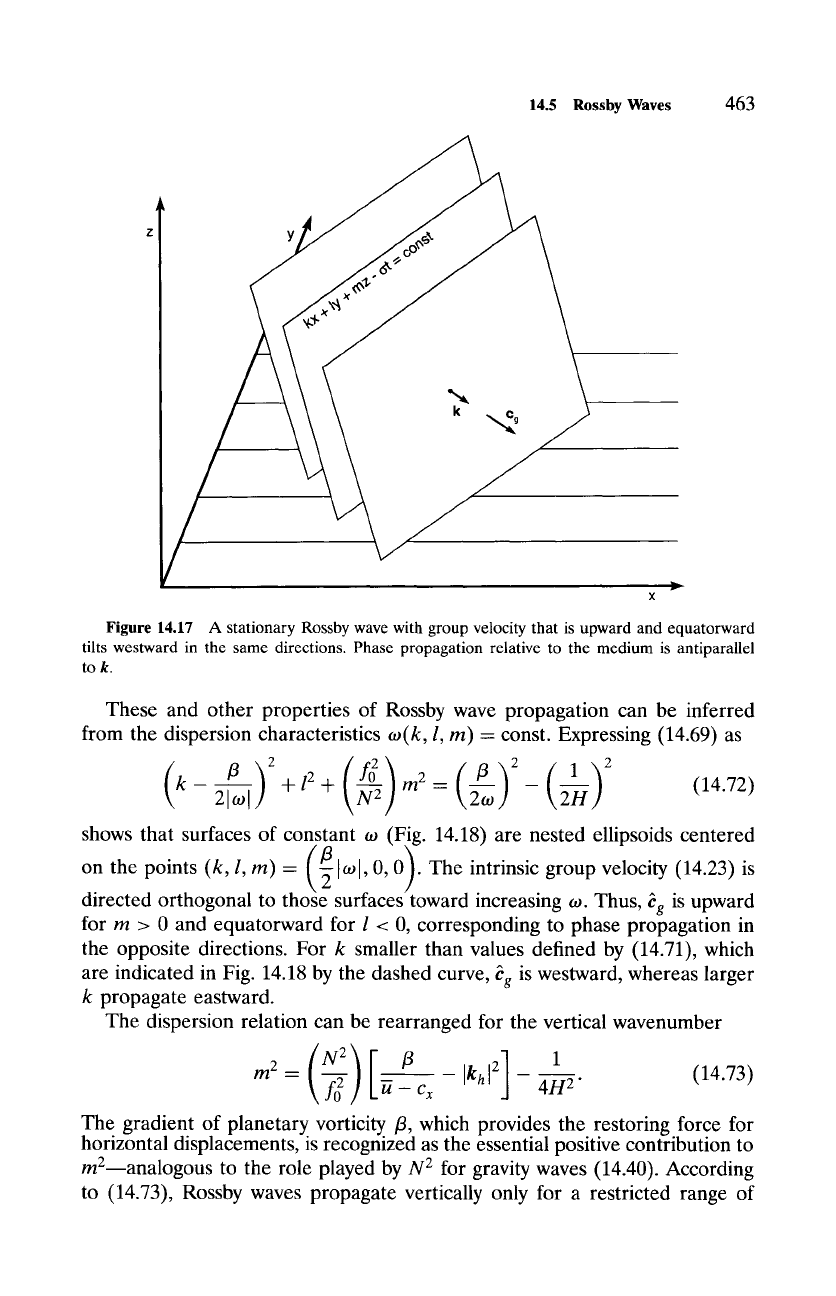
14.5

Rossby Waves

463

Figure 14.17

A stationary Rossby wave with group velocity that is upward and equatorward

tilts westward in the same directions. Phase propagation relative to the medium is antiparallel

to k.

These and other properties of Rossby wave propagation can be inferred

from the dispersion characteristics

w(k,

l, m) = const. Expressing (14.69) as

t (' lm2

k 2[wl + + ~ - ~ - ~ (14.72)

shows that surfaces of constant o) (Fig. 14.18) are nested ellipsoids centered

-I~ol,

0, 0 The intrinsic group velocity (14 23) is

on the points (k, l, m)- 2 "

directed orthogonal to those surfaces toward increasing ~o. Thus, g:g is upward

for m > 0 and equatorward for l < 0, corresponding to phase propagation in

the opposite directions. For k smaller than values defined by (14.71), which

are indicated in Fig. 14.18 by the dashed curve, g-g is westward, whereas larger

k propagate eastward.

The dispersion relation can be rearranged for the vertical wavenumber

( 2)E i 1

m 2 0

Ikhl 2

(14.73)

f2 -a Cx

4H 2"

The gradient of planetary vorticity/3, which provides the restoring force for

horizontal displacements, is recognized as the essential positive contribution to

m2--analogous to the role played by N 2 for gravity waves (14.40). According

to (14.73), Rossby waves propagate vertically only for a restricted range of

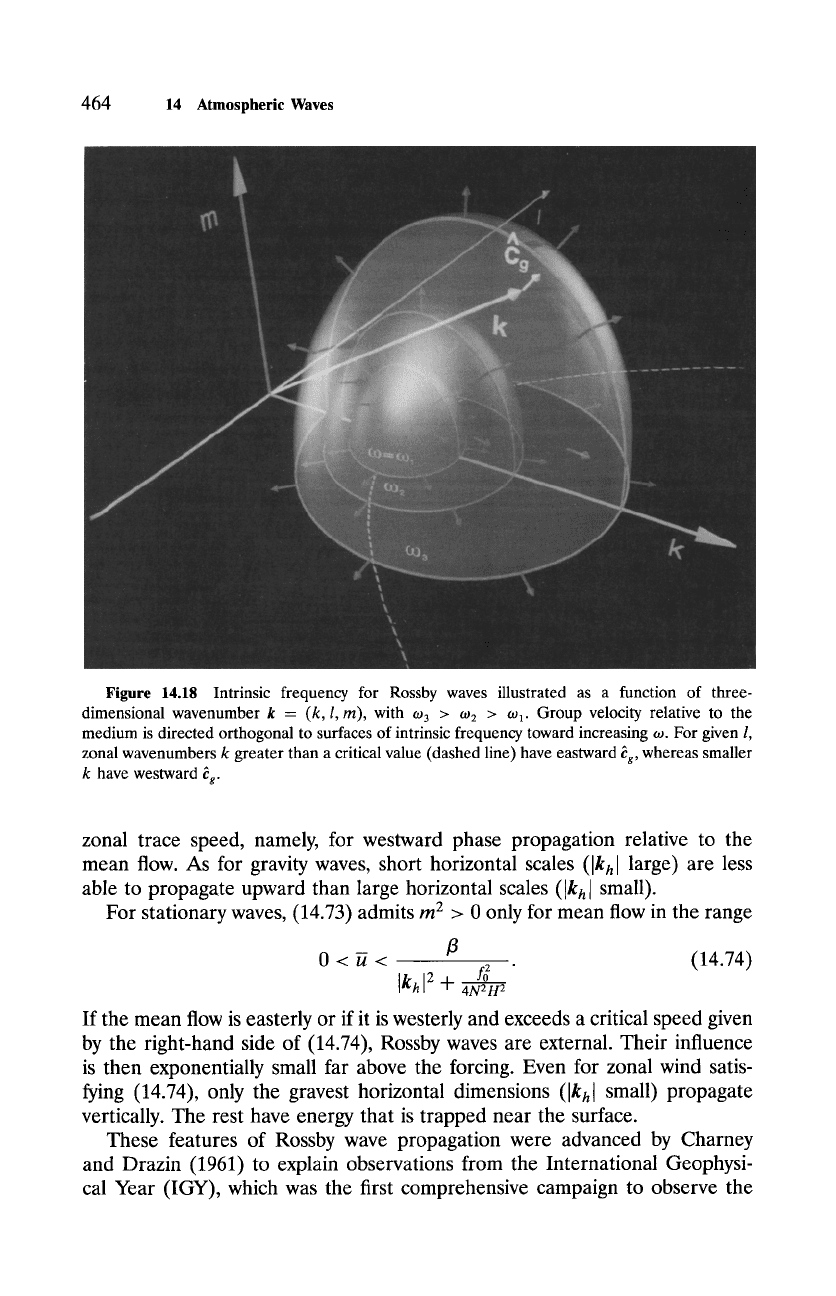
464

14 Atmospheric Waves

Figure

14.18 Intrinsic frequency for Rossby waves illustrated as a function of three-

dimensional wavenumber k = (k, I, m), with ~o 3 > to 2 > to 1. Group velocity relative to the

medium is directed orthogonal to surfaces of intrinsic frequency toward increasing to. For given 1,

zonal wavenumbers k greater than a critical value (dashed line) have eastward s whereas smaller

k have westward ~g.

zonal trace speed, namely, for westward phase propagation relative to the

mean flow. As for gravity waves, short horizontal scales ([khl large) are less

able to propagate upward than large horizontal scales ([kh[ small).

For stationary waves, (14.73) admits m 2 > 0 only for mean flow in the range

0 < K < . (14.74)

[khl 2§ f2

4N2H 2

If the mean flow is easterly or if it is westerly and exceeds a critical speed given

by the right-hand side of (14.74), Rossby waves are external. Their influence

is then exponentially small far above the forcing. Even for zonal wind satis-

fying (14.74), only the gravest horizontal dimensions

(Ikhl

small) propagate

vertically. The rest have energy that is trapped near the surface.

These features of Rossby wave propagation were advanced by Charney

and Drazin (1961) to explain observations from the International Geophysi-

cal Year (IGY), which was the first comprehensive campaign to observe the

14.5 Rossby Waves

465

atmosphere. Taken during 1958, observations from the IGY revealed that the

synoptic eddies which dominate the tropospheric circulation are conspicuously

absent in the stratosphere (refer to Figs 1.9 and 1.10). All eddy scales are ab-

sent from the time-mean circulation in the summer hemisphere, which is

nearly circumpolar. According to the preceding analysis, only planetary-scale

components of the wave spectrum can propagate into the strong westerlies

of the winter stratosphere (Fig. 1.8). Disturbances of smaller horizontal di-

mension encounter turning levels not far above the tropopause (Fig. 14.14),

below which they are trapped. During summer, stratospheric easterlies pre-

vent all horizontal scales from propagating vertically because Rossby waves

then encounter critical levels (Fig. 14.15), where Cx - u and wave activity is

absorbed.

Charney and Drazin argued that these features of the stratospheric flow pre-

vent kinetic energy, which is concentrated in the troposphere in synoptic-scale

eddies, from propagating to high levels. Were vertical propagation possible for

energy-bearing eddies in the troposphere, the

exp(z/2H)

amplification associ-

ated with stratification would produce enormous temperatures at high altitude

to yield a corona similar to the sun.

Easterly flow in the tropical troposphere has a similar effect by block-

ing wave propagation between hemispheres. Therefore, large orographic fea-

tures that produce amplified waves in the Northern Hemisphere exert only

a minimal influence on the Southern Hemisphere. These interhemispheric

differences combine to produce a broken storm track in the Northern Hemi-

sphere (e.g., where amplified wave motions reinforce and interfere with with

the zonal-mean jet) and a comparatively uniform one in the Southern Hemi-

sphere.

14.5.3 Planetary Wave Propagation in Sheared Mean Flow

Westerly mean flow during winter and equinox enables planetary-scale Rossby

waves to radiate into the middle atmosphere. Due to stratification of mass,

those waves amplify vertically. Where planetary wave activity propagates and

is absorbed can be understood from a ray-tracing analysis.

Consider zonal-mean flow that varies with latitude and height K- K(y, z).

Linearizing the quasi-geostrophic potential vorticity equation (12.49) and not-

ing that

-3q,/,~y - -~

leads to the perturbation potential vorticity equation

1 O f0 _O~' 3~'

V2~ ' + - +/3 -- O, (14.75 1)

p ~z -~P~z e-~X

where

(2)

1 o~ fo _3~

~ e -- ~ -- -U y y -p o~ Z -~ P -~Z

= (14.75.2)

466

Atmospheric Waves

represents the meridional gradient of zonal-mean vorticity and is referred to

beta effective.

According to (14.75), positive curvature of the basic flow re-

duces the effective restoring force to meridional displacements of air, whereas

negative curvature reinforces it~analogous to gravity wave propagation in

sheared flow (14.40).

Considering solutions of the form

exp[(z/2H)+ i(kx-

o-t)] transforms

(14.75) into a Helmholtz equation

O2aI/'~ " a (f2 oat/'~ " ) /,,2 o"

dy ----T + -~z

N 2

+ (y' z)~l' = 0, (14.76.1)

where

l,'2(y, Z) = _ ~e

k 2 _ f2

(14.76.2)

u -- c x

4NZH 2

represents a reduced two-dimensional index of refraction that describes prop-

agation in the

y-z

plane. Solutions oscillate in regions where

v2(y, z) > O,

whereas they are evanescent in regions where

v2(y, z) <_ O.

Hence, propaga-

tion is excluded from regions where

fie

is sufficiently small or g is sufficiently

strong. Should

-~(y, z) ~ Cx, v 2

becomes infinite and (14.76) is singular. The

critical region defined by this condition differs from that for gravity waves

because v 2 ~ +c~ on either side (compare Fig. 14.15b). So wave structure

oscillates rapidly on one side of the critical line but is sharply evanescent on

the other.

Analytical solutions to (14.76) exist only under very idealized circumstances.

But, within the framework of the WKB approximation, wave propagation can

be diagnosed in terms of monochromatic behavior along rays. The dispersion

relation then assumes the same form as (14.69), but with

fie

in place of/3.

Under these circumstances, propagation in the

y-z

plane is controlled by

f2) m 2

_ #e k 2 f2

(14.77)

12+ ~ - -~_c x

-4N2H 2,

which is analogous to (14.40.2) for gravity waves. Figure 14.19 shows rays

introduced into zonal-mean flow representative of the winter stratosphere.

Planetary wave activity radiating upward and northward into strengthening

westerlies of the polar-night jet encounters a turning line, where 12 + m 2 van-

ishes, and is reflected. Refracted equatorward toward easterlies, wave activity

along that ray then encounters a critical line, where o) and the group velocity

vanish, so the ray stalls out. Analysis similar to that in Sec. 14.3.4 for gravity

waves shows that, ahead of the critical line, planetary wave activity is frozen

in the medium and hence absorbed. Planetary wave activity radiating ini-

tially upward and equatorward encounters a critical line and is absorbed even

sooner. Dickinson (1968) used the foregoing analysis to explain observed am-

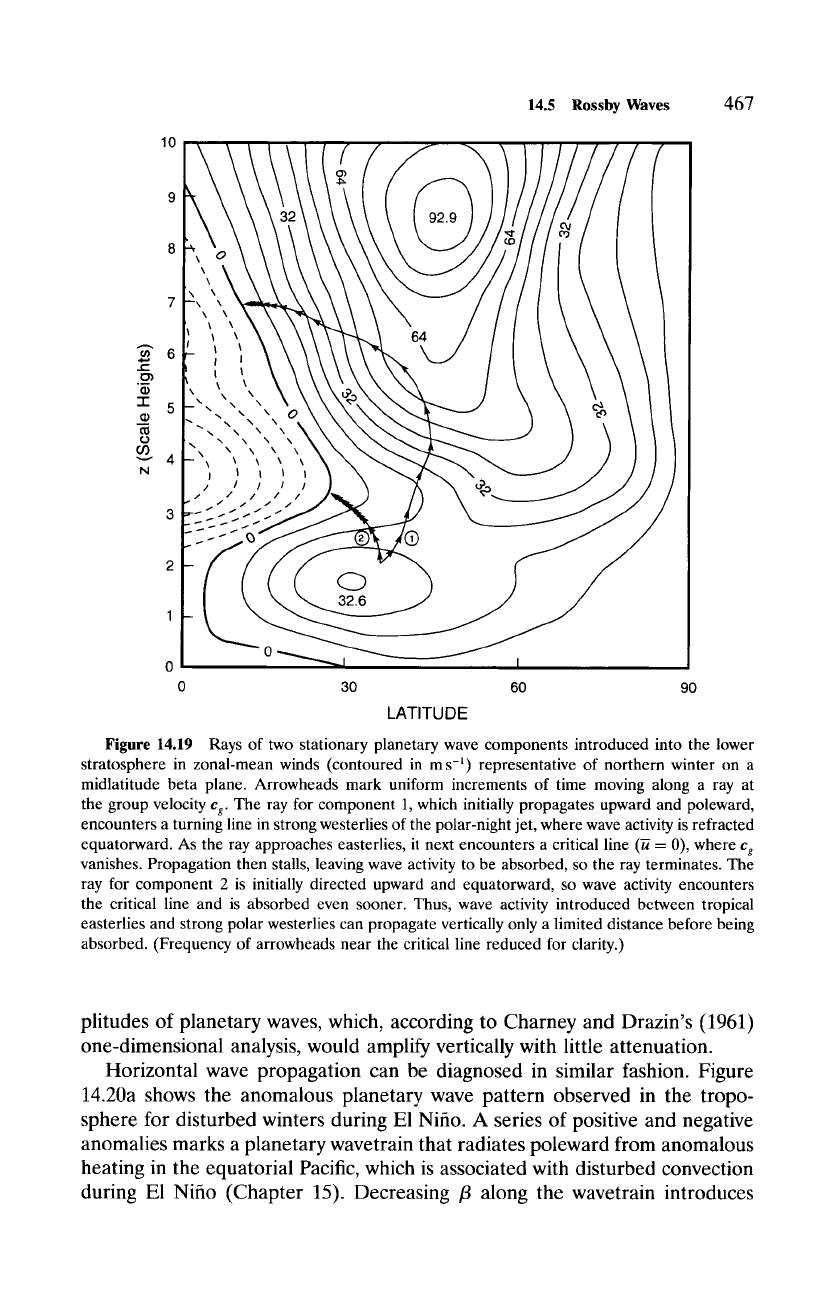
14.5 Rossby Waves

467

9 "r- 5

v 4

I l

, \ \

\\ 0

N %

~X\ \\ \\ \\

9 \ \ \ \

\\ \ \ \ \

I I I I I

/ / / /I I

/ / / /

~ .,, _

32.6

0 30 60 90

LATITUDE

Figure 14.19 Rays of two stationary planetary wave components introduced into the lower

stratosphere in zonal-mean winds (contoured in ms -i) representative of northern winter on a

midlatitude beta plane. Arrowheads mark uniform increments of time moving along a ray at

the group velocity

cg. The

ray for component 1, which initially propagates upward and poleward,

encounters a turning line in strong westerlies of the polar-night jet, where wave activity is refracted

equatorward. As the ray approaches easterlies, it next encounters a critical line (~ - 0), where

vanishes. Propagation then stalls, leaving wave activity to be absorbed, so the ray terminates. The

ray for component 2 is initially directed upward and equatorward, so wave activity encounters

the critical line and is absorbed even sooner. Thus, wave activity introduced between tropical

easterlies and strong polar westerlies can propagate vertically only a limited distance before being

absorbed. (Frequency of arrowheads near the critical line reduced for clarity.)

plitudes of planetary waves, which, according to Charney and Drazin's (1961)

one-dimensional analysis, would amplify vertically with little attenuation.

Horizontal wave propagation can be diagnosed in similar fashion. Figure

14.20a shows the anomalous planetary wave pattern observed in the tropo-

sphere for disturbed winters during E1 Nifio. A series of positive and negative

anomalies marks a planetary wavetrain that radiates poleward from anomalous

heating in the equatorial Pacific, which is associated with disturbed convection

during E1 Nifio (Chapter 15). Decreasing /3 along the wavetrain introduces

468

14 Atmospheric Waves

(a) A

---_______t~ 10 o N--'-'-T ~0C

160 o W 140 o 120 ~ _...-

Figure 14.20 (a) Anomalous planetary wave field for northern winters during E1 Nifio, when

anomalous convection (stippled) is positioned in the tropical central Pacific. The anomalous ridge

over western Canada and trough over the eastern United States characterize the so-called

Pacific

Noah America (PNA) pattern

that upsets the normal track of the jet stream (wavy trajectory) and

cyclone activity during E1 Nifio winters. After Horel and Wallace (1981); see Wallace and Gutzler

(1981) for a detailed plot.

(continues)

a turning latitude, where wave activity is reflected equatorward. Calculations

with convective heating in the tropical central Pacific (Fig. 14.20b) produce

similar structure, in particular, the prominent ridge over western Canada and

trough over the eastern United States that characterize the so-called Pacific

North America (PNA) pattern during E1 Nifio winters. By interfering with the

extratropical planetary wave field (e.g., as manifested in undulations of the jet

stream in Fig. 14.20a), those anomalies upset the normal pattern of cyclone

development, which controls weather in the troposphere.

14.6 Wave Absorption

In the absence of dissipation, wave activity is conserved following a wavepacket

(e.g., moving along a ray with the velocity

Cg)?

When dissipation is present,

5Amplitude, however, varies along a ray (14.41); see Lighthill (1978).

14.6

Wave Absorption

469

(b)

/ / ~ !/L_...." .: .......

' ",

\XX~/}

"i:~?~,,:~,X

\/\ \ -~ ,,,

:, ~ \

...~, ,, ,) ', i ..........

"' ~

""7\ ........... ', \ -- , ,, ...&"'~-; ,

// .... X .... .~,z.. ............ j. ................. i--:h:- .............. <" ", .... h'-,. ',,

/ \ i ~

/ ~

"...::::-:'-..~

~ ', ..:,~-::=....,:~.., "

') ...,., i '':.-.., ........... --,.., ...... i'ii ..... :::: ..... ",

~: : !

.............. " ..... ~i ............. .,'. ,'..~i

i ! ......................... .:., i ..... I ....... ~,..

....... i ! i i ,~ ..... [

......

i.. ! i i .../: ..... !

9 :

......... ~ z

.,~

......

~ !

':, i ............. i ........................ E~ ........... i ......................... i ~:: /

........ ~.... ! ~ ...

iiiiiiiiiiiiiiii

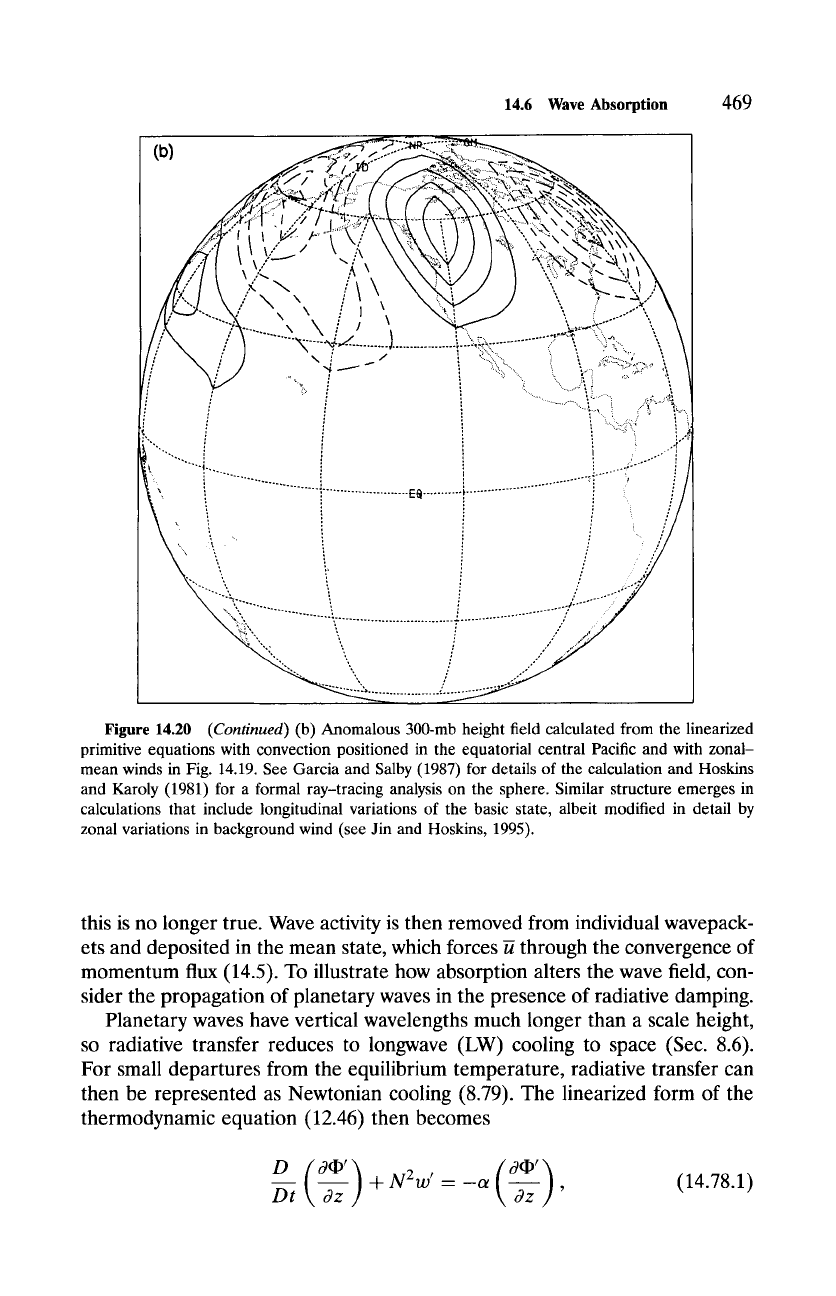
Figure 14.20

(Continued)

(b) Anomalous 300-mb height field calculated from the linearized

primitive equations with convection positioned in the equatorial central Pacific and with zonal-

mean winds in Fig. 14.19. See Garcia and Salby (1987) for details of the calculation and Hoskins

and Karoly (1981) for a formal ray-tracing analysis on the sphere. Similar structure emerges in

calculations that include longitudinal variations of the basic state, albeit modified in detail by

zonal variations in background wind (see Jin and Hoskins, 1995).

this is no longer true. Wave activity is then removed from individual wavepack-

ets and deposited in the mean state, which forces K through the convergence of

momentum flux (14.5). To illustrate how absorption alters the wave field, con-

sider the propagation of planetary waves in the presence of radiative damping.

Planetary waves have vertical wavelengths much longer than a scale height,

so radiative transfer reduces to longwave (LW) cooling to space (Sec. 8.6).

For small departures from the equilibrium temperature, radiative transfer can

then be represented as Newtonian cooling (8.79). The linearized form of the

thermodynamic equation (12.46) then becomes

Dt ~1 + \ Oz '

(14.78.1)