Salby M.L. Fundamentals of Atmospheric Physics

450 14 Atmospheric Waves

inhibits vertical propagation by reducing m 2. The vertical wavelength is then

elongated, which makes wave activity increasingly vulnerable to reflection.

If m 2 is driven to zero for a particular k, the vertical wavelength becomes

infinite (see Fig. 14.14b). Continued propagation is then forbidden and wave

activity is fully reflected. The height where this occurs is called the

turning

level,

above which wave structure is external (m 2 < 0). On the other hand,

decreasing

Cx--~

favors vertical propagation by increasing m 2. The vertical

wavelength is then shortened, which reduces reflection by making variations

in refractive properties comparatively gradual. Should

Cx--~

decrease to zero,

(14.40) becomes singular. The refractive index is then unbounded and the

vertical wavelength collapses to zero (see Fig. 14.15b). The height where this

occurs is called the

critical level.

Contrary to a turning level, which leads to

reflection, the condition m 2 --+ cx~ leads to absorption of wave activity.

14.3.3 The WKB Approximation

Analytical solutions to (14.40) can be obtained only for very idealized profiles

of N2(z) and K(z). But an approximate class of solutions that is valid when

the basic state varies slowly compared to the phase of oscillations affords

great insight into how wave activity propagates--even under more general

circumstances. The approximate solutions

W~(z) = W~ exp[+i f m(z) dz]

(14.41)

v/m(z)

satisfy the related equation

32W+

~z------ 2- + m2(z)W + = -R(z)m2(z)W +,

(14.42.1)

where

R(z)= 1 o2m

3 (0m) 2

2m 3 3z 2 4m 4 ~ (14.42.2)

symbolizes the interdependence of W + and W- and therefore wave reflection.

In the limit of R ~ 0 everywhere, (14.42) reduces to the general form of

(14.40). Reflection then vanishes and the upward- and downward-propagating

waves can be treated independently. In the absence of dissipation, wave ac-

tivity then propagates conservatively along

rays

that are smoothly refracted

through the medium. The solution (14.41) defines the so-called

slowly varying

or WKB

approximation. 3

Its validity (e.g., R < < 1 ) rests on refractive proper-

ties changing on a scale that is long compared to the wavelength. In practice,

(14.41) often provides a qualitatively correct description of the wave field even

3The letters stand for Wentzel (1926), Kramer (1926), and Brillouin (1926), who rediscovered

the procedure in different problems, after being introduced originally by Liouville (1837) and

Green (1838).

14.3 Buoyancy Waves

451

when it cannot be justified formally. Should R become O(1) somewhere, re-

flection introduces the other of the components in (14.41). Clearly, m 2 = 0

violates the aforementioned condition because the local wavelength is then

infinite, which is attended by strong reflection. Although the WKB approxi-

mation breaks down there, the wave field can be matched analytically across

the turning level (see, e.g., Morse and Feschbach, 1953).

14.3.4 Method of Geometric Optics

under conditions of the WKB approximation, wave activity can be traced from

its source along rays that are defined by the local group velocity

cg.

If

N 2

K= << ic ~ _ K[, (14.43)

(14.40.2) has the same form as the dispersion relation for simple gravity waves

in the short wavelength limit (14.36). Components of

cg

then follow from

(14.23) as

m2to

Cg x = k(k 2 +

m 2)

m

+u,

(14.44)

mr

Cg z=-(k 2+m2) '

with m =

m(z)

and K- K(z). Tangent to

Cg,

a ray has local slope in the

x-z

plane

dz Cgz

= (14.45)

.

dx r

Specifying its initial coordinates then determines the ray corresponding to an

individual component (k, m) of the wave spectrum.

TURNING LEVEL

Orographically forced gravity waves involve a spectrum about zero fre-

quency. Figure 14.14 shows rays of two components with o- - 0 under the

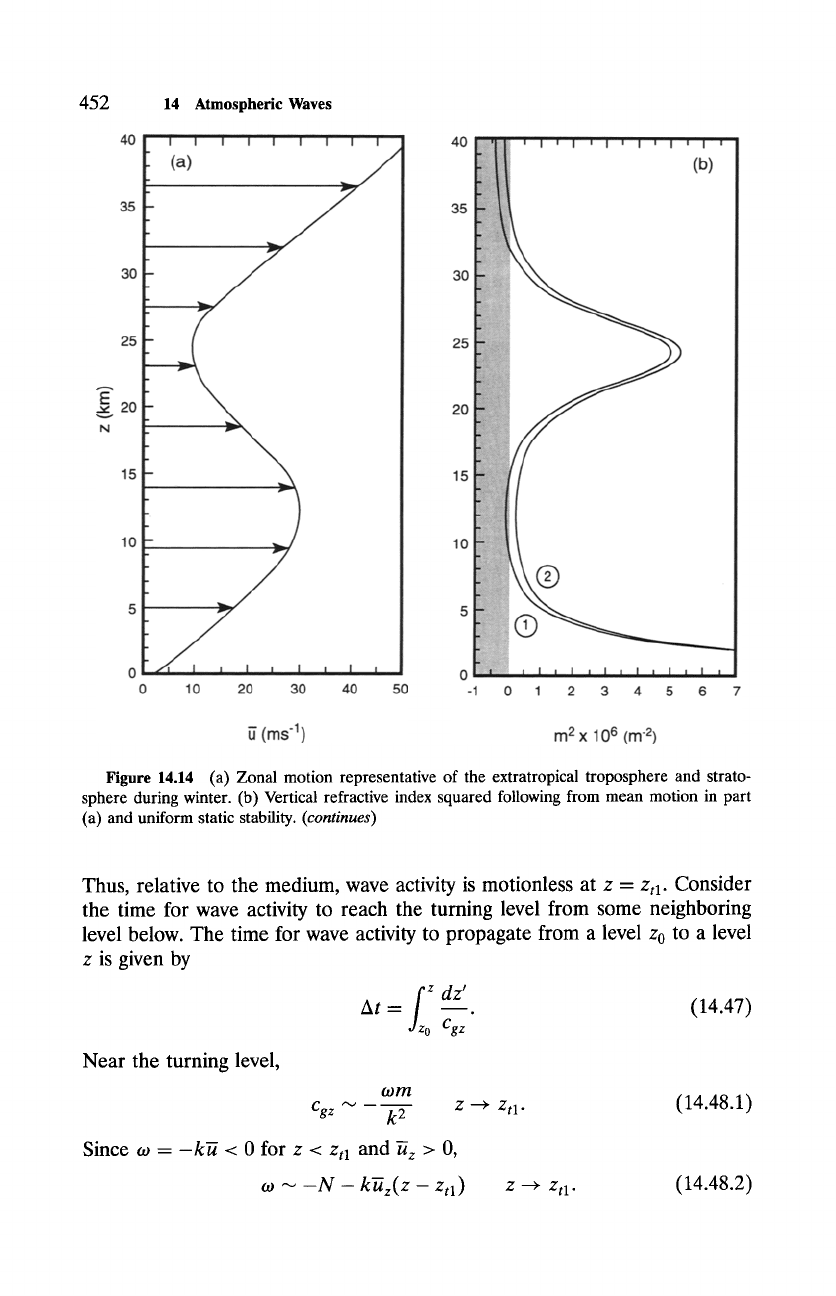
conditions of (14.43) for N2=const and ~(z) representative of the tropo-

sphere and wintertime stratosphere (Fig. 14.14a). Each ray emanates from a

point source located at the origin of the

x-z

plane. For component 1, which

has short horizontal wavelength, westerly shear drives o92 to N 2 and m 2 to zero

near the tropopause (Fig. 14.14b). The ray for that component (Fig. 14.14c)

is reflected at its turning level

Ztl,

above which wave amplitude decays expo-

nentially.

Since m- 0 at the turning level,

Cg x ~ lg

z- Ztl.

(14.46)

Cg~ - 0

452

14 Atmospheric Waves

40

35

I

" (a)

3~ f

25

N . v~

15

10

5

0 I ~ I

0 10 2o 30

|

(b)

40 50 -1 0 1 2 3 4 5 6 7

(ms "1) m 2 x 106 (m -z)

Figure 14.14 (a) Zonal motion representative of the extratropical troposphere and strato-

sphere during winter. (b) Vertical refractive index squared following from mean motion in part

(a) and uniform static stability.

(continues)

Thus, relative to the medium, wave activity is motionless at z =

ztl.

Consider

the time for wave activity to reach the tuming level from some neighboring

level below. The time for wave activity to propagate from a level z0 to a level

z is given by

fz~ dz'

At = ~. (14.47)

Cgz

Near the turning level,

o)m

z ~ Ztl.

(14.48.1)

cg z ~ _ k2

Since oJ = -k~ < 0 for z <

zta

and Uz > 0,

oJ ~ -N- k-~z(Z-

Ztl )

Z --+ Ztl.

(14.48.2)

40

35

14.3 Buoyancy Waves

i

f' j

................... Zt2 ............................................................

453

30

25

E

~, 20

v

N

1~[- |

10 I"- ....... ,,4' ......................................... Ztl

(9

0

0 5 10 15 20 25 30 35 40 45

x

(km)

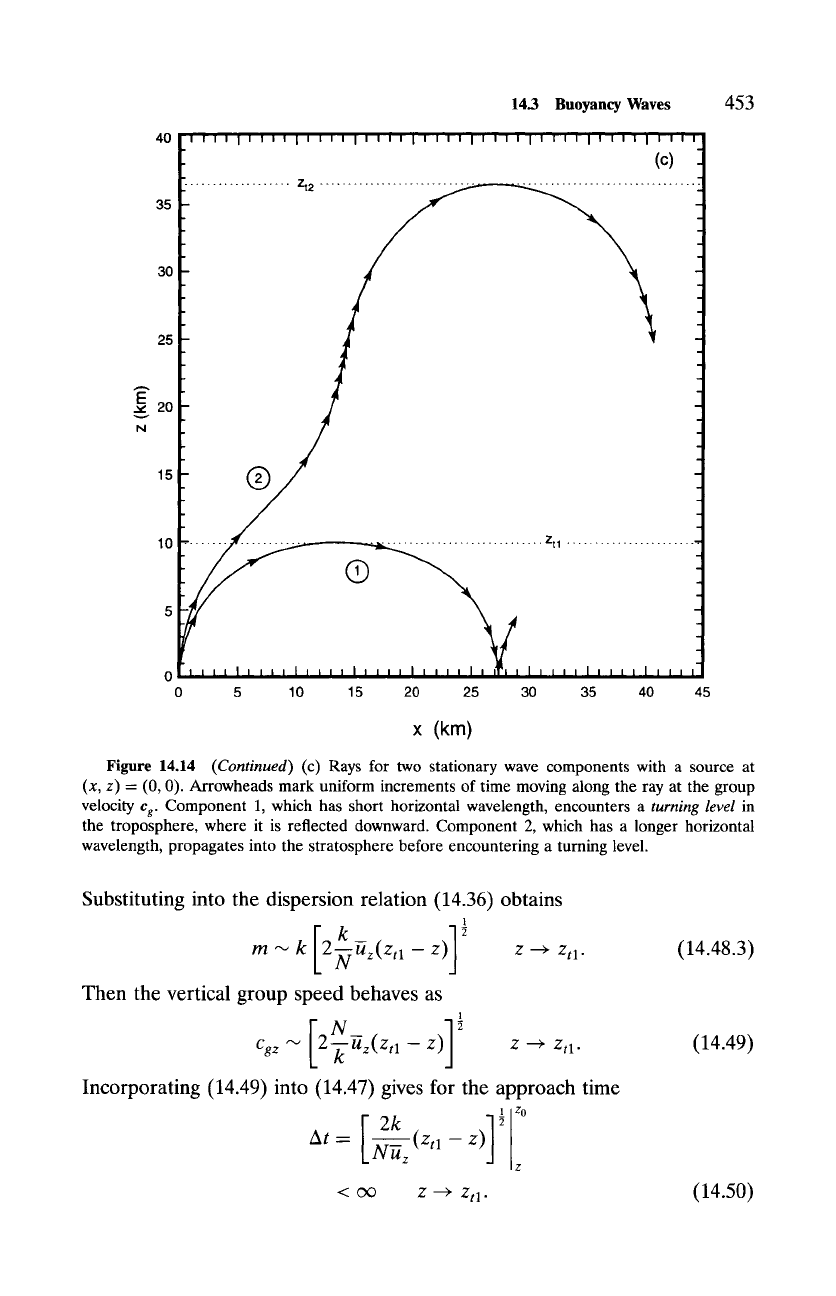
Figure 14.14

(Continued)

(c) Rays for two stationary wave components with a source at

(x, z) = (0, 0). Arrowheads mark uniform increments of time moving along the ray at the group

velocity

Cg.

Component 1, which has short horizontal wavelength, encounters a

turning level

in

the troposphere, where it is reflected downward. Component 2, which has a longer horizontal

wavelength, propagates into the stratosphere before encountering a turning level.

Substituting into the dispersion relation (14.36) obtains

k

m'~ k [2-~-Uz(Ztl - z)189

z ~ Ztl.

(14.48.3)

Then the vertical group speed behaves as

1

Cg z ~ (Ztl -- Z) Z ~ Ztl.

Incorporating (14.49) into (14.47) gives for the approach time

~u~u (z,, - ~tl ~

< co z----~ Ztl.

(14.49)

(14.50)

I I I I I

(bl

40

35

30

25

~ 20

N

15

10

5

0

-30 -20 -10 0 10 20

(ms -1)

454

14

Atmospheric Waves

l I i~l

0 10 20 30 40 50

m 2 x 106 (m "2)

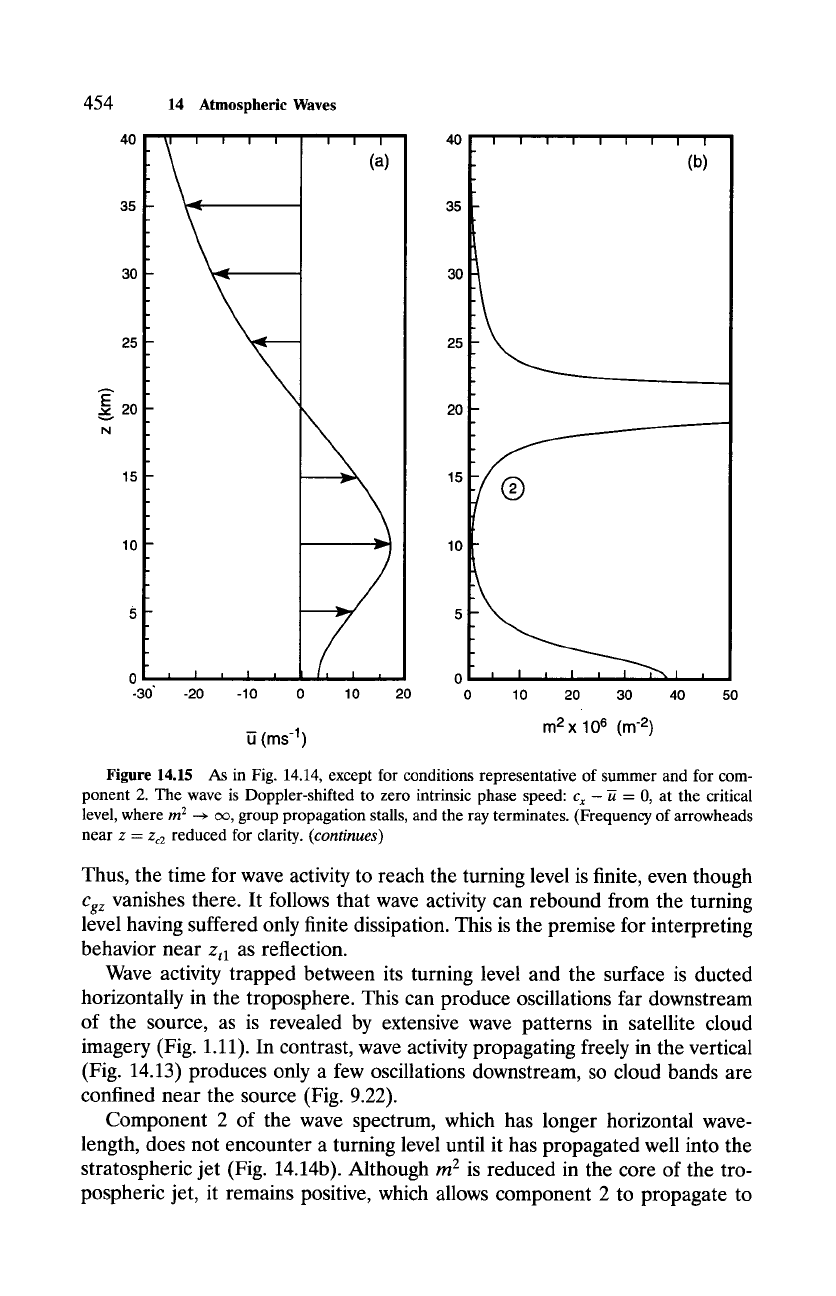
Figure 14.15 As in Fig. 14.14, except for conditions representative of summer and for com-

ponent 2. The wave is Doppler-shifted to zero intrinsic phase speed:

Cx

- ~ = 0, at the critical

level, where m 2 ~ ~, group propagation stalls, and the ray terminates. (Frequency of arrowheads

near z =

Zc2

reduced for clarity.

(continues)

Thus, the time for wave activity to reach the turning level is finite, even though

Cg z

vanishes there. It follows that wave activity can rebound from the turning

level having suffered only finite dissipation. This is the premise for interpreting

behavior near

Ztl

as reflection.

Wave activity trapped between its turning level and the surface is ducted

horizontally in the troposphere. This can produce oscillations far downstream

of the source, as is revealed by extensive wave patterns in satellite cloud

imagery (Fig. 1.11). In contrast, wave activity propagating freely in the vertical

(Fig. 14.13) produces only a few oscillations downstream, so cloud bands are

confined near the source (Fig. 9.22).

Component 2 of the wave spectrum, which has longer horizontal wave-

length, does not encounter a turning level until it has propagated well into the

stratospheric jet (Fig. 14.14b). Although m 2 is reduced in the core of the tro-

pospheric jet, it remains positive, which allows component 2 to propagate to

14.3 Buoyancy Waves

455

A

E

v

N

:35

-

30

25-

' I ' I ' I ' I ' I ' I ' I ' I ' I

(c)

20 ! ............................. Zc2

15

|

10

|

0 1 2 3 4 5 6 7 8 9 10

x (km)

Figure 14.15

(Continued)

higher levels. The region of small

m 2

in the upper troposphere coincides with

small vertical group speed. Propagation is then refracted into a shallower an-

gle (Fig. 14.14c), only to be refracted more steeply again when it encounters

weaker zonal flow in the lower stratosphere. Eventually, K in the stratospheric

jet becomes large enough to drive

m 2 to

zero, which occurs at the turning

level

zt2

and below which component 2 is vertically trapped.

CRITICAL LEVEL

Consider now conditions representative of summer. Figure 14.15 shows

the same features for component 2, but for easterly flow in the stratosphere.

Having Cx = 0, component 2 is Doppler-shifted to zero at the zero wind line,

which lies not far above the tropopause (Fig. 14.15a). At the critical level Zc2,

m 2 --+

cx~ and the vertical wavelength collapses to zero (Fig. 14.15b).

456

14 Atmospheric

Waves

Since w -0 at the critical level,

%x=K-O

z = Zc2,

(14.51)

Cg z -- 0

so wave activity is again motionless relative to the medium. Consider the time

for it to reach the critical level from some neighboring level z0 below. For z

near the critical level,

to

Cg z ~---- Z ~ Zc2.

(14.52)

m

Since ~o - -kg < 0 for z <

Zc2

and Uz < O,

to ~ -k-~z(Z- Zc2 )

Z ~ Zc2.

(14.53.1)

Substituting into the dispersion relation gives

N

m ~

z ~ Zc2.

(14.53.2)

-~z(Z- Zc2 )

Then the vertical group speed behaves as

_ r

--2 )2

(14.54)

Cg z ~-" u Uz,Z -

Zc2

Z

---+ Zc2.

By incorporating (14.54) into (14.47), we obtain for the approach time

N 17

At = -1

"---> O0 Z ~ Zc2.

(14.55)

Unlike behavior at a turning level, the time for wave activity to reach the

critical level is infinite. Thus, the critical level is never actually encountered.

Instead, wave activity remains frozen relative to the medium for infinite dura-

tion, allowing dissipation to absorb it. The ray for component 2 (Fig. 14.15c)

is then refracted into the critical level, where it stalls and terminates.

14.4 The Lamb Wave

Consider oscillations in an unbounded atmosphere and in the absence of

forcing. These conditions define an eigenvalue problem for the normal modes

of that system, namely, wave modes that can persist without forcing. Should

forcing exist at the corresponding eigenfrequencies, normal modes are greatly

amplified relative to other wave components.

For oscillations that are hydrostatic, the perturbation equations (14.33) re-

duce to

Du'

-- -gH Off

, (14.56.1)

Dt Ox

14.4 The Lamb Wave

457

H a )P' h'

Oz 1 + = 0, (14.56.2)

Dt~' Ou' (O l)w,=O, (14.56.3)

D--t- § Ox + Oz H

D

D---~(/3' - yt3') + 3' w' - 0. (14.56.4)

Considering solutions of the form

exp[i(kx -

~rt)] transforms (14.56) into

- iwU~ = -ikgHP~,

(14.57.1)

3-z 1 P~ + p~ - 0, (14.57.2)

-',wPk '~ +"kUk" +(OzO

H) Wff = 0 ,1 (14.57.3)

-iw(P~

- yp~)+ YHWff = 0. (14.57.4)

Using (14.57.2) to eliminate density in (14.57.4) gives

iWH(HO)

w~= K oz K P~ (14.58)

for the vertical velocity. Then, incorporating (14.58), (14.57.1), and (14.57.3)

yields a second-order differential equation for the perturbation amplitude

P~(z)

2 cr or k 2

0 Pk 10P~ Kg

3z 2 H Oz ~- -H--JPff

= 0. (14.59)

For physically meaningful behavior, solutions to (14.59) must satisfy bound-

ary conditions. At the surface, we require w' to vanish. The upper boundary

condition depends on whether the solution is vertically propagating or evanes-

cent. If the solution is evanescent, it must have bounded column energy. If it

is vertically propagating, at large distances from the source, the solution must

transfer wave activity away from regions of possible excitation (e.g., from finite

z). These conditions define the so-called

finite-energy

and

radiation conditions,

respectively, which apply at z ~ ec. Collectively,

P~(z)

must then satisfy

oZP~ 1 OP~ Kg

k 2 .,,~r

o~Z 2

H Oz ~- ~-~r~, - 0, (14.60.1)

H ~zz - K Pff =0 z--0, (14.60.2)

finite-energy/radiation z --+ ~. (14.60.3)

Equations (14.60) define a homogeneous boundary value problem for the

vertical structure

P~(z),

namely, one with no forcing in the interior or on

458

14 Atmospheric Waves

the boundaries of the domain. Nontrivial solutions can exist only at particular

frequencies.

Seeking solutions of the form exp[(1/2H + im)z] transforms (14.60.1) into

the dispersion relation

1

N 2

- ~k 2.

(14.61)

m 2 + 4H 2 -- CO 2

Equation (14.61) may be recognized as (14.35.2) in the limit k ~ 0, wherein

the horizontal wavelength is long enough for vertical displacements to be hy-

drostatic. If m 2 > 0, solutions are vertically propagating. By (14.44), upward

energy propagation (14.60.3) requires mo~ < 0, which corresponds to down-

ward phase propagation. For w > 0, this requires m < 0. It is readily verified

that these solutions do not satisfy the homogeneous lower boundary condition

(14.60.2). Nor do their counterparts for ~o < 0. If m 2 = -rh 2 < 0, the solu-

tions of (14.60.1) are external. The requirement of bounded column energy

then selects solutions of the form exp[(1/2H- rh)z]. One of these satisfies

the lower boundary condition, namely, th = (K- 89 which has the vertical

structure

P~(z) = e "(h). (14.62.1)

For this particular vertical structure, (14.61) reduces to

~2 __

ygH

2 (14.62.2)

C s .

The vertical structure (14.62), which defines the Lamb mode and is pictured

in Fig. 14.8b, makes w' vanish~not just at the surface, but everywhere (14.58).

Buoyancy oscillations then vanish identically. The restoring force for Lamb

waves is provided entirely by compressibility so they propagate at the speed

of sound (Fig. 14.9). Lamb waves are the normal modes of an unbounded,

compressible, stratified atmosphere. Even though their energy decreases up-

ward like an edge wave, Lamb waves amplify vertically, which makes them

potentially important in the upper atmosphere.

Because they are normal modes of the atmosphere, Lamb waves are excited

preferentially by forcing that is indiscriminate over frequency, for example, an

impulsive disturbance (Problems 14.33). The response spectrum to such forc-

ing is unbounded at those wavenumbers and frequencies satisfying (14.62.2),

so it is dominated by Lamb waves (Problem 14.32). Historical records in-

clude several impulses to the atmosphere that were felt around the earth.

Most notable was the eruption of Krakatoa in 1883 (Chapter 8). Disturbances

in surface pressure cycled around the globe several times before dissipating.

Taylor (1929) used barometric records to infer the vertical structure of at-

mospheric normal modes. By comparing arrival times at several stations, he

showed that the compression wave emanating from Krakatoa propagated at

14.5 Rossby Waves

459

the speed of sound. Then, with the aid of a system like (14.60), Taylor de-

duced the Lamb structure for atmospheric normal modes. A similar analysis

was performed by Whipple (1930) for the impact of the great Siberian meteor

in 1908. The Lamb vertical structure applies to atmospheric normal modes

at all frequencies, even very low-frequency waves supported by the earth's

rotation (Dikii, 1968).

14.5 Rossby Waves

At frequencies below 2f~, another class of wave motion exists, one possible

only in a rotating medium. Named for C. G. Rossby who established their

connection to weather phenomena (Rossby et al., 1939), these waves are also

referred to as rotational waves and, on the gravest dimensions, planetary waves.

The restoring force for Rossby waves is provided by the variation with latitude

of the Coriolis force, which links them directly to the earth's rotation.

14.5.1 Barotropic Nondivergent Rossby Waves

The simplest model of Rossby waves relies on the solenoidal character of

large-scale motion (Sec. 12.1). Under nondivergent conditions, atmospheric

motion is governed by conservation of absolute vorticity (12.30), which on a

beta plane is expressed by

d~

+/3v = 0.

dt

Linearizing about a basic state that is barotropically stratified and in uniform

motion, we obtain the perturbation vorticity equation

D~"

D---t- +/3v' - 0. (14.63)

The motion is nondivergent, so it can be represented in terms of a stream-

function

v~ - k • Vqd. (14.64)

Then the perturbation vorticity equation becomes

~,'

O V2 ~, -~- ~ --

0, (14.65)

Dt dx

which is just the linearized form of the barotropic nondivergent vorticity equa-

tion ( 12.31).

Known as the Rossby wave equation, (14.65) reflects a balance between

changes in the relative vorticity of an air parcel and changes in its planetary

vorticity due to meridional displacement. An eastward-moving parcel deflected

Salby M.L. Fundamentals of Atmospheric Physics

Подождите немного. Документ загружается.