Salby M.L. Fundamentals of Atmospheric Physics

Подождите немного. Документ загружается.

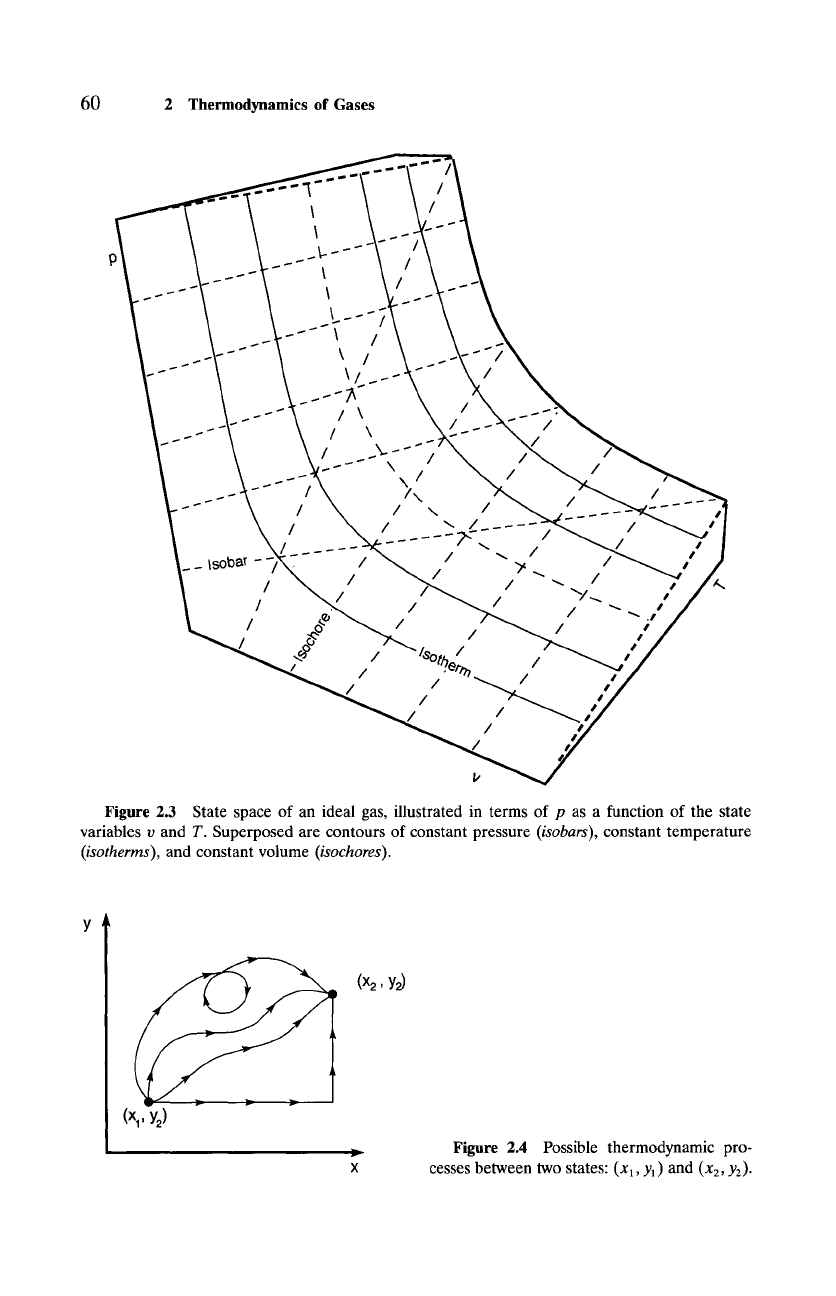
60 2 Thermodynamics of Gases

_ Isobar

......, W "" "" "" "

. ..---"

~ /

\ /

\/ . ..--

/ \ --~"

/ \ ...---7

'),. /

/ / \ / __ ----

\ /_ ,,

/ / / ~.~

.....

/ i

"~x / ,,

'~.// ~/~ ,,

"--,>...

- ,

/ / / ~ .,,

/ .

/ ~oth^~ /

""-..~'

/ / ~ / t

/ / ~

~ /

Figure 2.3 State space of an ideal gas, illustrated in terms of p as a function of the state

variables v and T. Superposed are contours of constant pressure

(isobars),

constant temperature

(isotherms),

and constant volume

(isochores).

v r r v

(x~, y~)

(X2,

Y2)

Figure 2.4 Possible thermodynamic pro-

cesses between two

states: (Xl, Yl)

and

(X2, y2)o

2.1 Thermodynamic Concepts

The incremental change of a quantity

z(x, y)

satisfying (2.5) may be repre-

sented as an exact differential"

3z d

dz -- 3z dx +

(2.6)

o-~ ~ y'

which is true only under certain conditions.

Exact Differential Theorem

Consider two continuously differentiable functions

M(x, y)

and

N(x, y)

in a simply connected region of the

x-y

plane. The contour integral

between two points (x0, Y0) and (x, y)

f(x x'y)

o,Yo)

M(x', y')dx' + N(x', y') dy'

(2.7)

(e.g., along a specified contour

g(x, y)

relating x and y) is path indepen-

dent if and only if

3M 3N

3y ,~x

(2.8)

Under these circumstances, the quantity

M(x, y)dx + N(x, y)dy - dz

represents an exact differential. That is, there exists a function z such that

M(x, y) -

3X'

U(x, y) - --,

in which case the contour integral (2.7) reduces to

(2.9)

z(x,y)

(xo,yo)

dz - z(x, y)- Z(Xo, Yo)

= Az

z - z(x, y) + c.

The variable defined by (2.7) is a

point function:

It depends only on the

evaluation point (x, y), and its net change along a contour depends only on

the initial and final points of the contour. Because it is unique only up to

2 Thermodynamics of

Gases

an additive constant, only changes of a point function are significant. Also

referred to as a

potential function, z(x, y)

defines an

irrotational

vector field I

v--Vz

= M(x, y)i + N(x, y)/',

(2.10.1)

which satisfies

v - 0. (2.10.2)

Conversely, an irrotational vector field may be represented as the gradient of

a scalar potential z. Gravity g is an irrotational vector field: V x g = 0. The

work performed to displace a unit mass between two points in a gravitational

field is independent of path and defines the gravitational potential ~.

Thermodynamic state variables are point functions. As properties of the

system, they depend only on the system's state but not on its history. By

contrast, the work performed by the system and the heat transferred into it

during a thermodynamic process are not properties of the system. Work and

heat transfer are, in general,

path functions.

They depend on the path in state

space followed by the system. For this reason, the thermodynamic process

must be specified to define those quantities unambiguously.

Path-dependent, work and heat transfer can differ along the forward and

reverse legs of a cyclic process. Consequently, the net work and heat transfer

during a cyclic variation of the system need not vanish, as does the net change

of a state variable (2.5). The path dependence of work and heat transfer

produces a

hysteresis

in the

w-q

plane, illustrated in Fig. 2.5. During a cyclic

variation of the system, the cumulative work and heat

w= f 6w

and

q= f 6q

do not return to their original positions after the system has been restored to

its initial state. The discrepancy

Aw -- f 6w

after one cycle equals the area in

the

p-v

plane enclosed by the contour in Fig. 2.2. Due to hysteresis, successive

cycles lead to a drift of the above quantities in the

w-q

plane, which reflects

the net work performed by and the heat transferred into the system.

Under special circumstances, the work performed by a system or the heat

transferred into it "is" independent of path, in which case that quantity does

vanish for a cyclic process. Because it is then a point function, this special form

of work or heat transfer can be used to define a state variable. For instance,

the displacement work in a gravitational field is path independent. Hence,

that work can then be used to define the gravitational potential ~, which is a

property of the system.

If it refers to force, the vector field v is said to be

conservative

because the net work performed

along a cyclic path vanishes (2.5).

2.2

The First Law

Figure 2.5 Cumulative work and heat transfer during successive thermodynamic cycles of

the system. The path dependence of w and q introduces a hysteresis into those quantities, even

though the system (i.e., any state variable) is restored to its initial state after each cycle.

2.2 The First Law

2.2.1 Internal Energy

The first law of thermodynamics is inspired by the observation that the work

performed on an adiabatic system is independent of the process, that is, it

is independent of the path in state space followed by the system. For an

adiabatic process, expansion work depends only on the initial and final states

of the system, so it behaves as a state variable. The

internal energy u

is defined

as that state variable whose difference equals the work performed on the

system under adiabatic conditions, or minus the work performed "by" the

system under adiabatic conditions

Au = --Wad.

(2.11.1)

For an incremental process,

du = --6Wad,

(2.11.2)

where 6 refers to an incremental change that is, in general, path dependent,

and d to one that is path independent (i.e., of a state variable). Under the

special circumstances defined earlier, work is path independent, so the net

work performed during a cyclic process vanishes. It follows that the system

returns to its initial state along the same path it followed out of that state.

2.2.2 Diabatic Changes of State

Consider now a diabatic process, as illustrated in Fig. 2.6. Because heat is

exchanged with the environment,

w # Wad = --AU.

Thermodynamics of Gases

Figure 2.6 An air parcel undergoing a process

between states 1 and 2, during which it performs

work w and absorbs heat q.

The work performed by the system w will differ from that performed under

adiabatic conditions

Wad

by an

amount q, which equals the energy transferred

"into" the system through heat exchange. Hence,

Au = q- w. (2.12.1)

Equation (2.12.1) constitutes the

first law of thermodynamics.

For an incre-

mental process and for a system capable of expansion work only, the first law

can be expressed

du = 6q- pdv.

(2.12.2)

In (2.12),

pdv

represents the work performed "by" the system on its surround-

ings and q the heat transfer "into" the system. Although the change of internal

energy between two states is path independent, the same is not true of the

work performed by the system and the heat transferred into it. Except under

adiabatic conditions, the work performed by the system during a change of

state depends on the thermodynamic process. Likewise, except under special

circumstances, the heat transferred into the system depends on the path fol-

lowed in state space. Since each is path dependent, neither the work nor the

heat transfer vanishes for a cyclic process. However, the change of internal

energy does vanish for a cyclic process, in which case the first law reduces to

fpdv=f6q.

(2.13)

The net work performed by the system during a cyclic process is balanced by

the net heat absorbed by the system.

A closed system that performs work through a conversion of heat absorbed

by it is said to be a

heat engine.

Conversely, a system that rejects heat through a

2.3 Heat Capacity 65

9 2

conversion of work performed on it is a

refrtgerator.

We will see in Chapter 6

that individual air parcels comprising the circulation of the troposphere behave

as a heat engine. By absorbing heat at the earth's surface through transfers

of radiative, sensible, and latent heat, and by rejecting heat in the upper

troposphere through LW emission to space, air parcels perform net work as

they evolve through a thermodynamic cycle (refer to Fig. 1.27). According

to (2.13), the net work performed during such a cycle equals the net heat

absorbed by the parcel. That work is ultimately realized as kinetic energy,

which maintains the circulation of the troposphere against frictional dissipation

and makes it thermally driven.

In contrast, the circulation of the stratosphere behaves as a radiative re-

frigerator. For vertical motion to occur, individual air parcels must have work

performed on them, which is eventually rejected to space in the form of LW

radiation. In that sense, the circulation of the stratosphere is mechanically

driven. Gravity waves and planetary waves that propagate upward from the

troposphere and are dissipated in the stratosphere exert an influence analo-

gous to paddle work. By rearranging stratospheric air, those disturbances drive

the circulation out of radiative equilibrium, which results in net IR cooling to

space.

It is convenient to introduce the state variable

enthalpy

h -- u + pv.

(2.14)

In terms of enthalpy, the first law becomes

dh = 6q + vdp.

(2.15)

Enthalpy is useful for diagnosing processes that occur at constant pressure.

Under those circumstances, the first law reduces to a statement that the change

in enthalpy equals the heat transferred into the system.

2.3 Heat Capacity

Observations indicate that the heat absorbed by a homogeneous system which

is maintained at constant pressure or at constant volume is proportional to the

change of the system's temperature. The constants of proportionality between

heat absorption and temperature change define the

specific heat capacity at

constant pressure

6qp

(2.16.1)

Cp = dT

2 In some texts, the term

refrigerator

refers to a particular type of heat engine. However, we

reserve this term for a system that converts work into heat and use the term

heat engine

exclusively

for a system that converts heat into work.

66 2

Thermodynamics of Gases

and the

specific heat capacity at constant volume

~qv (2.16.2)

cv= dT'

where the subscripts denote

isobaric

(p = const) and

isochoric

(v = const)

processes, respectively.

The specific heat capacities are related closely to the internal energy and

enthalpy of the system. Because they are state variables, u and h can be

expressed in terms of any two other state variables. For instance, u =

u(v, T),

in which case

du = du dv + dT.

T v

Incorporating this transforms the first law (2.12.2) into

() ]

du dT + ~ + p dv= 6q.

v 7"

For an isochoric process, this reduces to

(O~T) = 'qv

~, dT

=co. (2.17.1)

Thus, the specific heat capacity at constant volume measures the rate internal

energy increases with temperature during an isochoric process. In a similar

fashion, the enthalpy may be expressed h =

h(p, T),

with which the first law

(2.15) becomes

[ (~~--~hT) r

v]dp+(~T)pdT='q"

For an isobaric process, this reduces to

~ p dr

=cp.

(2.17.2)

The specific heat capacity at constant pressure measures the rate enthalpy

increases with temperature during an isobaric process.

In a strict sense, cp and cv are state variables, so they depend on pressure

and temperature. However, over ranges of pressure and temperature relevant

to the atmosphere, the specific heats may be regarded as constant. Therefore,

the change of internal energy during an isochoric process is proportional to the

change of temperature alone and similarly for the change of enthalpy during

an isobaric process. It turns out that, for an ideal gas, the relationships (2.17)

hold irrespective of process.

2.3 Heat Capacity 67

Consider the internal energy of an ideal gas in the form u = u(p, T).

Joule's experiment, which is pictured in Fig. 2.7, demonstrates that u is then a

function of temperature alone. Two ideal gases that are initially isolated and

at pressures Pl and P2 are brought into contact and allowed to equilibriate,

for example, by rupturing a diaphragm that separates them. Observations

indicate that no heat transfer takes place with the environment during this

process. Then the first law reduces to a statement that the change of internal

energy equals minus the work performed. However, the volume of the system

(that occupied by both gases) does not change, so the work also vanishes and

Au = 0. Yet, the final equilibrated pressure clearly differs from the initial

pressures of the two gases in isolation. Since the total internal energy of the

system equals the sum of the contributions from the two cells, it follows that

u is not a function of pressure. Therefore,

u(p, T) reduces to

u = u(T),

which must hold regardless of process for an ideal gas. Incorporating this result

and the ideal gas law into (2.14) demonstrates that the enthalpy is likewise a

function of temperature alone

h =

which again holds irrespective of process.

Based on these conclusions, equations (2.17) are valid in general for an ideal

gas. Integrating with respect to temperature yields finite values of internal

energy and enthalpy, which are unique up to constants of integration. It is

customary to define u and h so that they vanish at a temperature of absolute

zero. With that convention,

u =cvT, (2.18.1)

h --cpT,

(2.18.2)

It follows that

Cp - c,, = R. (2.19)

According to statistical mechanics, the specific heat at constant volume is

given by

- 3R (2.20.1)

cv 2

Figure 2.7 Schematic of Joule's experi-

ment: Two ideal gases in states 1 and 2 are

brought into contact by rupturing a diaphragm

that separates them initially. No heat transfer

with the surroundings is observed.

2 Thermodynamics

of Gases

for a monotomic gas, and by

c v - ~R (2.20.2)

for a diatomic gas (e.g., Lee, Sears, and Turcotte, 1973). These values are con-

firmed experimentally over a wide range of pressure and temperature relevant

to the atmosphere. Taking air to be chiefly diatomic together with the value

of Rd in (1.18) yields the specific heats for dry air

Cvd --

717.5 J kg -1K -1,

(2.21.1)

Cpd-

1004.5 J kg -1 K -1,

and the dimensionless constants

"y- Cp/C v --

1.4, (2.21.2)

K--R/Cp

= (y- 1)/y

0.286. (2.21.3)

With the aforementioned definitions, the first law can be expressed in the

two equivalent forms:

c,,dT + pdv- 6q,

(2.22.1)

cpdT- vdp- 6q.

For isochoric and isobaric processes, these expressions reduce to

6% -- cvdT,

(2.22.2)

(2.23.1)

6qp = cpdT,

(2.23.2)

respectively. Because the right-hand sides of (2.23) involve only state variables,

the same must be true of the left-hand sides. Thus, under these special cir-

cumstances, heat transfer behaves as a state variable. Although generally path

dependent, heat transfer during an isochoric process or during an isobaric

process is uniquely determined by the change of temperature.

2.4 Adiabatic Processes

For an adiabatic process, the first law reduces to

cvdT + pdv - O,

(2.24.1)

cpdT - vdp - O.

(2.24.2)

2.4

Adiabatic Processes

Dividing through by T and introducing the the gas law transforms (2.24) into

cvdln T + Rdln

v = 0, (2.25.1)

cpd

T - Rd

In p = 0,

which may be integrated to obtain the identities

T cv

V R ---

const

(2.25.2)

(2.26.1)

TCp p-R

= const. (2.26.2)

A third identity, which relates p and

can be derived from (2.25) with the

aid of a differential form of the ideal gas law

din p + dln v = dln T, (2.27)

which follows from (1.1). Using (2.27) to eliminate T from (2.25.2) gives

cvd

p + cpd

In v = 0, (2.28)

which on integration yields

pCvvCp

= const. (2.29)

The three identities, (2.26.1), (2.26.2), and (2.29), can be cast in terms of

dimensionless constants as

Tv 7-1 =

const, (2.30.1)

Tp -~

= const, (2.30.2)

pv ~

= const. (2.30.3)

Known as

Poisson's equations,

(2.30) define adiabatic paths in the state space

of an ideal gas. Each describes the evolution of a state variable during an

adiabatic process in terms of only one other state variable. Thus, the change of

a single state variable together with the condition that the process be adiabatic

is sufficient to determine the change of a second state variable and hence the

change of thermodynamic state. For this reason, an adiabatic system possesses

only one independent state variable and thus only one thermodynamic degree

of freedom.

Because the state space of a pure substance is represented by the plane of

any two intensive properties zl and z2, a thermodynamic process describes a

contour

g(za, z2) = const.

Poisson's equations (2.30) are of this form and describe a family of contours,

known as

adiabats,

in the plane of any two of the state variables p, T, and v

(Fig. 2.8). In a similar fashion, isobaric processes describe a family of

isobars

(p = const), isothermal processes describe a family of

isotherms

(T = const),