Salby M.L. Fundamentals of Atmospheric Physics
Подождите немного. Документ загружается.


80 3
The Second Law and Its Implications
Figure 3.1 A gas at the system pressure Ps that is acted on by a piston with pressure pp and
is maintained at constant temperature through contact with a heat reservoir.
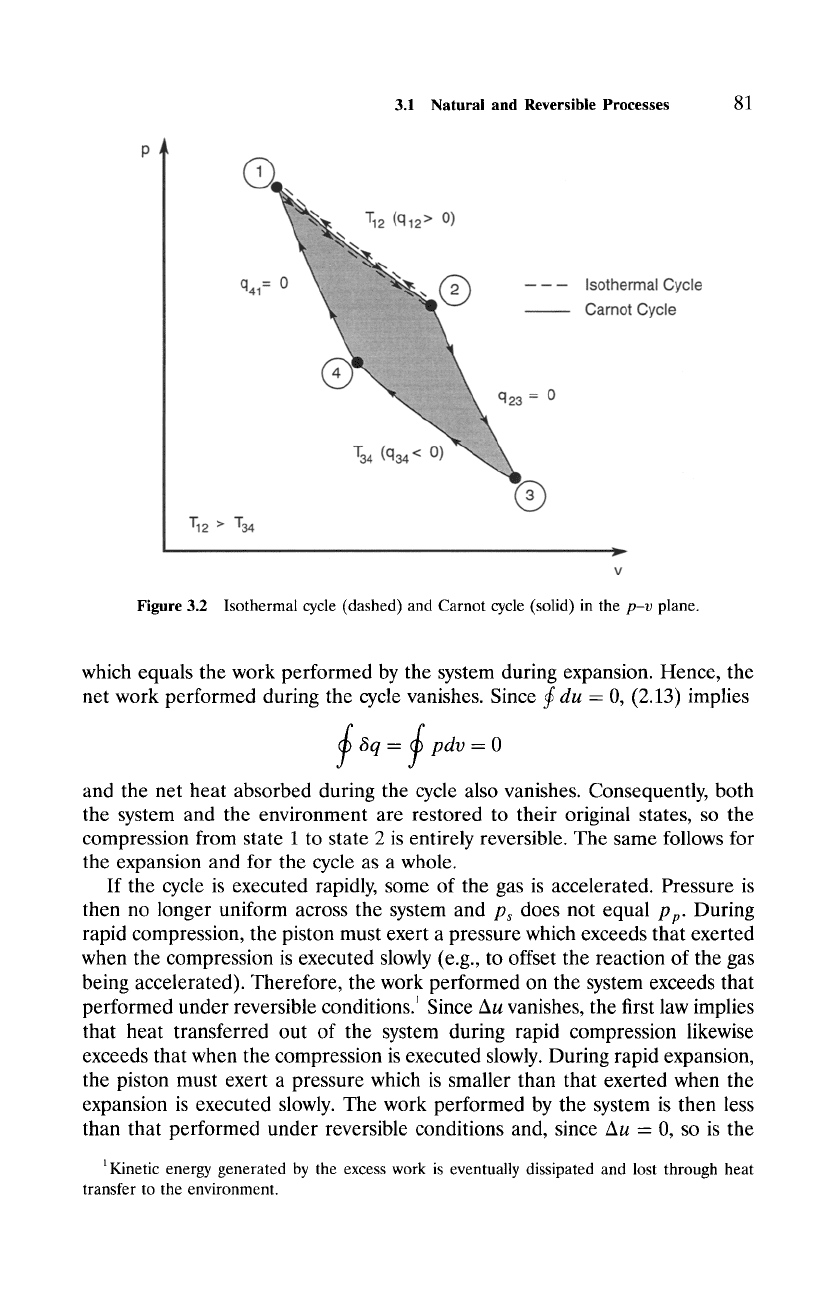
isothermal compression at the same temperature (Fig. 3.2). If the cycle is ex-
ecuted very slowly and without friction, the system pressure p~ is uniform
throughout the gas and equals that exerted by the piston
p p
at each stage of
the process. Therefore, the work performed by the system during expansion is
given by
W12 __
f2
ppdv
f2 RT12 dv
,11
v
v2
- RTI2 In (~11) 9
Likewise, the work performed on the system during compression is
--W21 -- --
f21
ppdv
=RT121n(V2) '01
(3.1.1)
(3.1.1)
3.1
Natural and Reversible Processes
81
q41 = 0
T12 > T34
T12 (q 12 > O)
(~ Isothermal Cycle
Carnot Cycle
T34 (q34 < O)
q23 = 0
Figure
3.2 Isothermal cycle (dashed) and Carnot cycle (solid) in the
p-v
plane.
which equals the work performed by the system during expansion. Hence, the
net work performed during the cycle vanishes. Since
f du
= 0, (2.13) implies
f, q-fpdv-o
and the net heat absorbed during the cycle also vanishes. Consequently, both
the system and the environment are restored to their original states, so the
compression from state 1 to state 2 is entirely reversible. The same follows for
the expansion and for the cycle as a whole.
If the cycle is executed rapidly, some of the gas is accelerated. Pressure is
then no longer uniform across the system and
Ps
does not equal
pp.
During
rapid compression, the piston must exert a pressure which exceeds that exerted
when the compression is executed slowly (e.g., to offset the reaction of the gas
being accelerated). Therefore, the work performed on the system exceeds that
performed under reversible conditions. ~ Since Au vanishes, the first law implies
that heat transferred out of the system during rapid compression likewise
exceeds that when the compression is executed slowly. During rapid expansion,
the piston must exert a pressure which is smaller than that exerted when the
expansion is executed slowly. The work performed by the system is then less
than that performed under reversible conditions and, since Au ---_ 0, so is the
1Kinetic energy generated by the excess work is eventually dissipated and lost through heat
transfer to the environment.

82
3
The Second Law and Its Implications
heat transferred into the system. Thus, executing the isothermal cycle rapidly
results in
f pdv = f 6q < O.
Net work is performed on the system, which must be compensated by net
rejection of heat to the environment.
This example illustrates that completing a transition between two states
reversibly minimizes the work that must be performed on a system and maxi-
mizes the work that is performed by the system. These results can be extended
to a system that performs work through a conversion of heat transferred into
it, namely, to a heat engine. With (2.13), it follows that the cyclic work per-
formed by such a system is maximized when the cycle is executed reversibly.
Irreversibility reduces the net work performed by the system over a cycle,
which must be associated with some heat rejection to the environment.
3.1.1 The Carnot Cycle
Consider a cyclic process comprised of two isothermal legs and two adiabatic
legs (Fig. 3.2). During isothermal expansion and compression, the system is
maintained at constant temperature through contact with a thermal reservoir,
which serves as a heat source or heat sink. During adiabatic compression and
expansion, the system is thermally isolated. If executed reversibly, this process
describes a
Carnot cycle.
The leg from state 1 to state 2 is isothermal expansion
at temperature T12, so
AL/12 -- 0.
Then the heat absorbed during that leg is given by
q12 -- w12
- f12pdv
=RTa21n(V2) "vl
The leg from state 2 to state 3 is adiabatic, so
(3.2.1)
q23 -- 0
and
--W23 -- AU23
= co(T34 -
Z12 ).
(3.2.2)

3.1
Natural and Reversible Processes
83
Similarly, the leg between states 3 and 4 is isothermal compression, so the heat
transfer and work are given by
q34-w34-RT341n(V-~33), (3.2.3)
whereas the leg between states 4 and 1 is adiabatic, so it involves work
W41 --
cv(Zl2 -
T34 ). (3.2.4)
If the cycle is executed in reverse, the work and heat transfer during each leg
are exactly cancelled by those during the corresponding leg of the forward
cycle. Therefore, the Carnot cycle is reversible.
During the two adiabatic legs of (3.2.2) and (3.2.4), the work performed
cancels, while the heat transfer vanishes identically. Hence, the net work and
heat transfer over the cycle follow from the isothermal legs alone. The volumes
in (3.2.1) and (3.2.3) are related to the changes of temperature along the
adiabatic legs, which follow from Poisson's identity (2.30.1)
y-1
T12T34 --(V~-~)')'-I--(~I 4)
Thus,
1) 2 1) 3
1) 1 1) 4
Collecting the heat transferred during the isothermal legs yields
1)4
f6q--RT1eln(~11 )
-i- RT34 In (~33)
= R(T12 - T34)In (v~-12) ,
which is positive for T12
> T34
if v2 > va. Then
(3.3)
(3.4)
f pdv-
f
6q
> O. (3.5)
The system performs net work, which is converted from heat absorbed during
the cycle.
The Carnot cycle is a paradigm of a heat engine. For net work to be per-
formed by the system, heat must be absorbed at high temperature T12 (during
isothermal expansion) and rejected at low temperature T34 (during isothermal
compression). According to (3.2), more heat is absorbed at high temperature
than is rejected at low temperature. The first law (2.13) then implies that net
heat absorbed during the cycle is balanced by net work performed by the sys-
tem. If the preceding cycle is executed in reverse, the system constitutes a

84
3 The Second Law and Its Implications
refrigerator. More heat is rejected at high temperature than is absorbed at
low temperature. Then (2.13) asserts that net heat rejected during the cycle
must be compensated by work performed on the system.
Net work and heat transfer over the cycle are proportional to the tempera-
ture difference T12-
T34
between the heat source and heat sink. Not all of the
heat absorbed by the system during expansion is converted into work. Some
of that heat is rejected during compression. Therefore, the efficiency of a heat
engine is limited--even for a reversiblecycle.
3.2 Entropy and the Second Law
In the development of the first law, we observed that work is independent of
path under adiabatic conditions, which allowed the internal energy be intro-
duced as a state variable. The second law of thermodynamics is inspired by
the observation that the quantity
q/T
is independent of path under reversible
conditions. As for the first law, this allows the introduction of a state vari-
able,
entropy,
which is defined in terms of a quantity that is, in general, path
dependent.
Consider the Carnot cycle. According to (3.4),
f 6q=R
[In (V~a) (v~)]
-T +In =0,
which is equivalent to the identity
q1____22 -I- q4____l_l _ 0.
(3.6)
r12 T41
It turns out this relationship holds under fairly general circumstances.
Carnot's Theorem
The identity (3.6) holds for any reversible cycle between two heat reser-
voirs at temperatures
T12
and T41, irrespective of details of the cycle.
It can be shown that any reversible cycle can be represented as a succession of
infinitesimal Carnot cycles (e.g., Keenan, 1970). Therefore, Carnot's theorem
implies that the identity
6q
f (T)rev--0 (3.7)
holds irrespective of path.
By the exact differential theorem (Sec. 2.1.4), it follows that the quantity
(x y)
(6q/T)rev
represents a point function. That is,
f~x'.,
x(6q/T)rev
depends only
on the thermodynamic state (x, y) and not on the ~ l~at'~ along which the system

3.2 Entropy and the Second
Law 85
evolved to that state. In the spirit that internal energy was introduced (Sec.
2.2), we define the state variable entropy
rev
which constitutes a property of the system.
Carnot's theorem and the identity (3.7) apply to a reversible process. Under
more general circumstances, the following inequality holds.
The Clausius Inequality
For a cyclic process,
f~q
-T < 0, (3.9)
where equality applies if the cycle is executed reversibly.
One of several statements of the second law, the Clausius inequality has the
following consequences that pertain to the direction of thermodynamic pro-
cesses:
1. Heat must be rejected to the environment somewhere during a cycle.
2. Under reversible conditions, more heat is exchanged at high temper-
ature than at low temperature.
3. Irreversibility reduces the net heat absorbed during a cycle.
The first consequence precludes the possibility of a process that converts heat
from a single source entirely into work: a perpetual motion machine of the sec-
ond kind. Some of the heat absorbed by a system that performs work must be
rejected. Representing a thermal loss, that heat rejection limits the efficiency
of any heat engine, even one operated reversibly. The second consequence of
(3.9) implies that net work is performed by the system during a cycle (namely,
it behaves as a heat engine) if heat is absorbed at high temperature and
rejected at low temperature. Conversely, net work must be performed on the
system during the cycle (namely, it behaves as a refrigerator) if heat is rejected
at high temperature and absorbed at low temperature. The third consequence
of (3.9) implies that irreversibility reduces the net work performed by the sys-
tem, in the case of a heat engine, and increases the net work that must be
performed on the system, in the case of a refrigerator.
A differential form of the second law, which applies to an incremental pro-
cess, may be derived from the Clausius inequality. Consider a cycle comprised
of a reversible and an irreversible leg between two states 1 and 2 (Fig. 3.3). A
cycle comprised of two reversible legs may also be constructed between those
states. For the first cycle, the Clausius inequality yields
2 8q 1
f (_~_)revq_f2 (t~q
)
~/irrev ~
0,
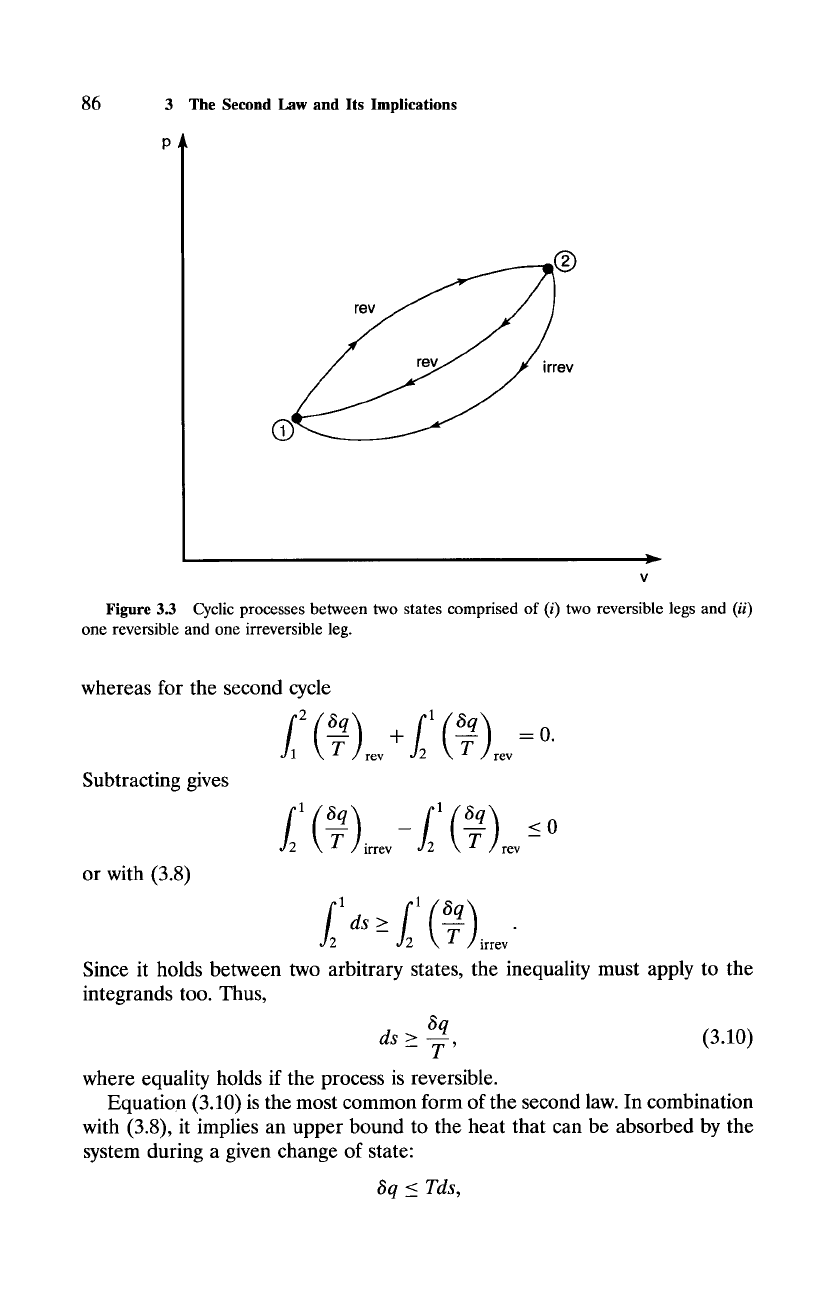
86
3
The Second Law and Its Implications
v
v
Figure 3.3 Cyclic processes between two states comprised of (i) two reversible legs and
(ii)
one reversible and one irreversible leg.
whereas for the second cycle
~12(-~)revd-~21 (-~)rev--O"
Subtracting gives
or with (3.8)
f2 a ( 6q 1
--T-) -f2 (6q
irrev -T-) rev ~ 0
ds >
irrev
Since it holds between two arbitrary states, the inequality must apply to the
integrands too. Thus,
6q
ds
> (3.10)
- T'
where equality holds if the process is reversible.
Equation (3.10) is the most common form of the second law. In combination
with (3.8), it implies an upper bound to the heat that can be absorbed by the
system during a given change of state:
6q <_ Tds,

3.3 Restricted
Forms of the Second Law
87
namely, the heat absorbed when that process is executed reversibly. If the
process is executed irreversibly, additional heat is rejected to the environment.
This reduces
6q
and the net heat absorbed, which in turn reduces the net work
performed by the system if the process is cyclic (2.13).
Also represented in (3.10) is the direction of thermodynamic processes.
Through the inequality, the second law asserts whether or not a system is
capable of evolving along a given path. A process for which the change of
entropy satisfies (3.10) is possible. If (3.10) is satisfied through equality, that
process is reversible, whereas if it is satisfied through inequality that process
is irreversible (e.g., a natural process). By contrast, a process that satisfies the
reverse inequality is impossible.
3.3 Restricted Forms of the Second Law
The entropy of a system can either increase or decrease, depending on the
heat transfer needed to achieve the same change of state under reversible
conditions. For certain processes, the change of entropy implied by the second
law is simplified.
For an adiabatic process, (3.10) reduces to
dSad > O,
(3.11)
so the entropy can then only increase. It follows that irreversible work increases
a system's entropy. Letting the control surface of a hypothetical system pass to
infinity eliminates heat transfer to the environment and leads to the conclusion
that the entropy of the universe can only increase. For a reversible adiabatic
process, (3.11) implies
ds
= 0, so such a process is
isentropic.
For an isochoric process, wherein expansion work vanishes, the first law
(2.23.1) transforms (3.8) into
ds-c~
-T- rev"
Since it involves only state variables, this expression must hold whether or not
the process is reversible. Hence,
- -T (3.12)
In the absence of work, entropy can either increase or decrease, depending
on the sign of
dT.
It follows that heat transfer can either increase or decrease
a system's entropy.
According to (3.11) and (3.12), changes of entropy follow from
1. Irreversible work and
2. Heat transfer.

88 3 The Second Law and Its Implications
Irreversible work only increases s, whereas heat transfer (irreversible or oth-
erwise) can either increase or decrease s. In the absence of work, the change
of entropy equals 6q/T, irrespective of path (e.g., whether or not the process
is reversible).
3.4 The Fundamental Relations
Substituting the second law (3.10) into the two forms of the first law (2.22)
leads to the inequalities
du < Tds- pdv, (3.13.1)
dh < Tds + vdp. (3.13.2)
For a reversible process, these reduce to
du = Tds- pdv, (3.14.1)
dh = Tds + vdp. (3.14.2)
Since they involve only state variables, the equalities (3.14) cannot depend on
path. Consequently, they must hold whether or not the process is reversible.
Known as the fundamental relations, these identities describe the change in
one state variable in terms of the changes in two other state variables. Even
though generally valid, the fundamental relations cannot be evaluated easily
under irreversible conditions. The values of p and T in (3.14) refer to the
pressure and temperature "of the system," which can be specified only under
reversible conditions. Under irreversible conditions, the relationship among
these variables reverts to the inequalities (3.13), wherein p and T denote
"applied values," which can be specified.
It is convenient to introduce two new state variables, that are referred to
as auxiliary functions. The Helmholtz function is defined by
f- u- Ts. (3.15.1)
The Gibbs function is defined by
g=h- Ts
= u + pv- Ts. (3.15.2)
In terms of these variables, the fundamental relations become
df = -sdT- pdv, (3.16.1)
dg = -sdT + vdp. (3.16.2)

3.4 The Fundamental Relations
89
The Helmholtz and Gibbs functions are each referred to as the
free energy
of the system: f for an isothermal process and g for an isothermal-isobaric
process, because they reflect the energy available for conversion into work
under those conditions (Problem 3.10).
3.4.1 The Maxwell Relations
Variables appearing in (3.14) and (3.16) are not entirely independent. Involv-
ing only state variables, each fundamental relation has the form of an exact
differential. According to the exact differential theorem (2.8), these relations
can hold only if the cross derivatives of the coefficients on the right-hand sides
are equal. Applying that condition to (3.14) and (3.16) yields the identities
(
Os
p
(3.17)
which are known as the
Maxwell relations.
3.4.2 Noncompensated Heat Transfer
The inequalities in (3.13) account for additional heat rejection to the environ-
ment that occurs through irreversibility. Those inequalities can be eliminated
in favor of equalities by introducing the
noncompensated heat transfer 3q',
defined by
6q = Tds- 6q',
(3.18)
where
6q'
> 0. The noncompensated heat transfer represents the additional
heat that must be rejected to the environment as a result of irreversibility, for
example, that associated with frictional dissipation of kinetic energy.
Substituting (3.18) into the first law (2.22.1) yields
du = Tds- pdv- 6q',
(3.19)
where p and T are understood to refer to applied values. An expression
for the noncompensated heat transfer can be derived from (3.14) and (3.19),
