Salby M.L. Fundamentals of Atmospheric Physics

Подождите немного. Документ загружается.

3 The Second Law and Its Implications

which hold for applied values under reversible and irreversible conditions,

respectively. Subtracting gives

~qt __ (T - Trev)ds - (p -

Prev)dl), (3.20)

where Trev and Prev refer to applied values under equilibrium conditions (i.e.,

those assumed by the system when the process is executed reversibly). Ac-

cording to (3.20), noncompensated heat transfer results from the thermal dis-

equilibrium of the system, which is represented in the difference T- Tre v, and

from the mechanical disequilibrium of the system, which is represented in the

difference p- Prev"

3.5 Conditions for Thermodynamic Equilibrium

By defining the direction of thermodynamic processes, the second law implies

whether or not a path out of a given thermodynamic state is possible. Since

this determines the likelihood of the system remaining in that state, the second

law characterizes the stability of thermodynamic equilibrium.

Consider a system in a given thermodynamic state. An arbitrary infinitesimal

process emanating from that state is referred to as a

virtualprocess. The

system

is said to be in

stable

true thermodynamic equilibrium

if no virtual process

emanating from that state is a natural process, i.e., if all virtual paths out of

that state are either reversible or impossible. If all virtual paths out of the

state are natural processes, the system is said to be in

unstable equilibrium. A

small perturbation will then result in a finite change of state. If only some of

the virtual processes out of the state are natural, the system is said to be in

metastable equilibrium.

A small perturbation then may or may not result in a

finite change of state, depending on the details of the perturbation.

These definitions can be combined with the second law to determine con-

ditions that characterize thermodynamic equilibrium. The relations

du < Tds- pdv,

dh < Tds + vdp,

df <_ -sdT- pdv,

dg <_ -sdT + vdp,

hold for a reversible process, in the case of equality, and for an irreversible

(e.g., natural) process, in the case of inequality. For a state to correspond to

thermodynamic equilibrium, the reverse must be true, that is,

du > Tds- pdv,

dh >_ Tds + vdp,

df > -sdT- pdv,

(3.21)

dg > -sdT + vdp,

3.6 Relationship of

Entropy to Potential Temperature

where inequality describes an impossible process. Inequalities (3.21) provide

criteria for thermodynamic equilibrium. If they are satisfied by all virtual pro-

cesses out of the current state, the system is in true thermodynamic equilib-

rium. If only some virtual paths emanating from the state satisfy (3.21), the

system is in metastable equilibrium.

Under special circumstances, simpler criteria for thermodynamic equilib-

rium exist. For an adiabatic enclosure, (3.10) reduces to

ds>_O,

where inequality corresponds to a natural process. Then a criterion for ther-

modynamic equilibrium is

dSad <

(3.22)

which describes reversible and impossible processes. According to (3.22), a

state of thermodynamic equilibrium for an adiabatic system coincides with a

local maximum of entropy (Fig. 3.4). Therefore, an adiabatic system's entropy

must increase as it approaches thermodynamic equilibrium.

Choosing processes for which the right-hand sides of (3.21) vanish yields

other criteria for thermodynamic equilibrium:

dus, v > O,

dhs, p > O,

df ~,v > O,

dg~,p >_0,

(3.23)

which must be satisfied by all virtual paths out of the current state for the

system to be in equilibrium. For the particular processes just discussed, (3.23)

implies that a state of thermodynamic equilibrium coincides with local minima

in the properties u, h, f, and g, respectively. Thus, for those processes the

internal energy, enthalpy, Helmholtz function, and Gibbs function must all

decrease as a system approaches thermodynamic equilibrium.

3.6 Relationship of Entropy to Potential Temperature

In Chapter 2, we saw that the change of potential temperature is proportional

to the heat absorbed by an air parcel. Under reversible conditions, (3.10)

implies that the same is true of entropy. Substituting (2.36) into the second

3 The Second Law and Its Implications

Figure 3.4 Local entropy

maximum in the

u-v

plane, symbolizing a state that corresponds

to thermodynamic

equilibrium.

law yields

din 0

_< ~,

(3.24)

where equality holds for a reversible process. Because it involves only state

variables, that equality must hold irrespective of whether or not the process is

reversible. Hence,

d In 0 -

~, (3.25)

and the change of potential temperature is related directly to the change of

entropy. Despite its validity, (3.25) applies to properties of the system (e.g., to

3.6 Relationship of Entropy to Potential Temperature

p and T through 0). Thus, like the fundamental relations, it can be evaluated

only under reversible conditions.

3.6.1 Implications for Vertical Motion

If a process is adiabatic,

= 0 and

ds >_ O.

The entropy remains constant or

it can increase through irreversible work (e.g., that associated with frictional

dissipation of kinetic energy). In the case of an air parcel, the conditions

for adiabatic behavior are closely related to those for reversibility. Adiabatic

behavior requires not only that no heat be transferred across the control sur-

face, but also that no heat be exchanged between one part of the system and

another (e.g., Landau

et al.,

1980). The latter requirement excludes turbu-

lent mixing, which is the principal form of mechanical irreversibility in the

atmosphere. It also excludes irreversible expansion work because such work

introduces internal motions that eventually result in mixing.

Since they exclude the important sources of irreversibility, the conditions

for adiabatic behavior are tantamount to conditions for isentropic behavior.

Thus, adiabatic conditions for the atmosphere are equivalent to requiring isen-

tropic behavior for individual air parcels. Under these circumstances, potential

temperature surfaces, 0 = const, coincide with isentropic surfaces, s = const.

An air parcel coincident initially with a certain isentropic surface remains on

that surface. Because those surfaces tend to be quasi-horizontal, adiabatic be-

havior implies no net vertical motion (see Fig. 2.9). Air parcels can ascend

and descend along isentropic surfaces, but they undergo no systematic vertical

motion.

Under diabatic conditions, an air parcel moves across isentropic surfaces

according to the heat exchanged with its environment (2.36). Consider an

air parcel advected horizontally through different thermal environments, like

those represented in the distribution of net radiation in Fig. 1.27. Because

radiative transfer varies sharply with latitude, this occurs whenever the par-

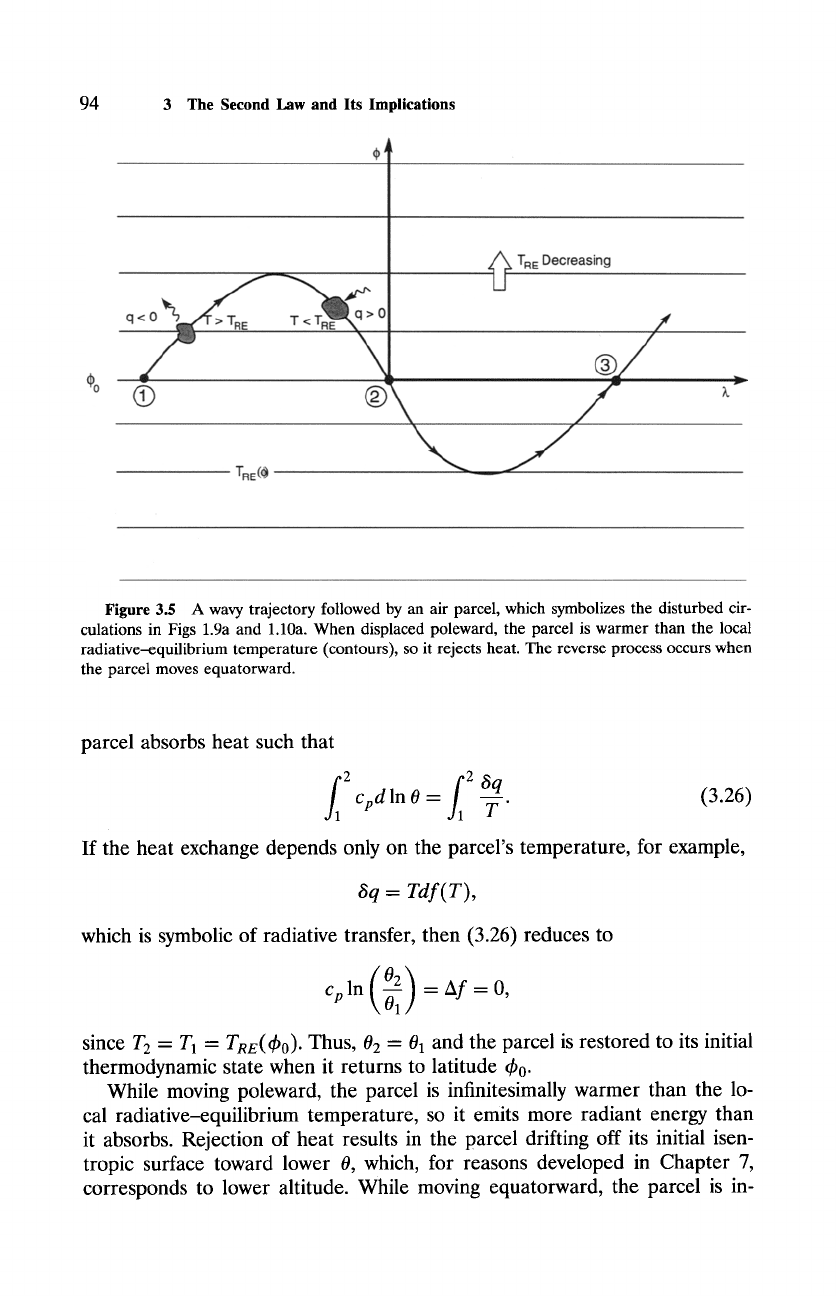
cel's motion is deflected across latitude circles. Figure 3.5 shows a wavy

trajectory followed by an air parcel that is initially at latitude ~b 0. Sym-

bolic of the disturbed circulations in Figs. 1.9 and 1.10, that motion ad-

vects air through different radiative envil'onments. Also indicated in Fig. 3.5

is the distribution of radiative-equilibrium temperature TRz(~b), at which air

emits radiant energy at the same rate as it absorbs it. That thermal struc-

ture is achieved if the motion is everywhere parallel to latitude circles, be,

cause air parcels then have infinite time to adjust to local thermal equili-

brium.

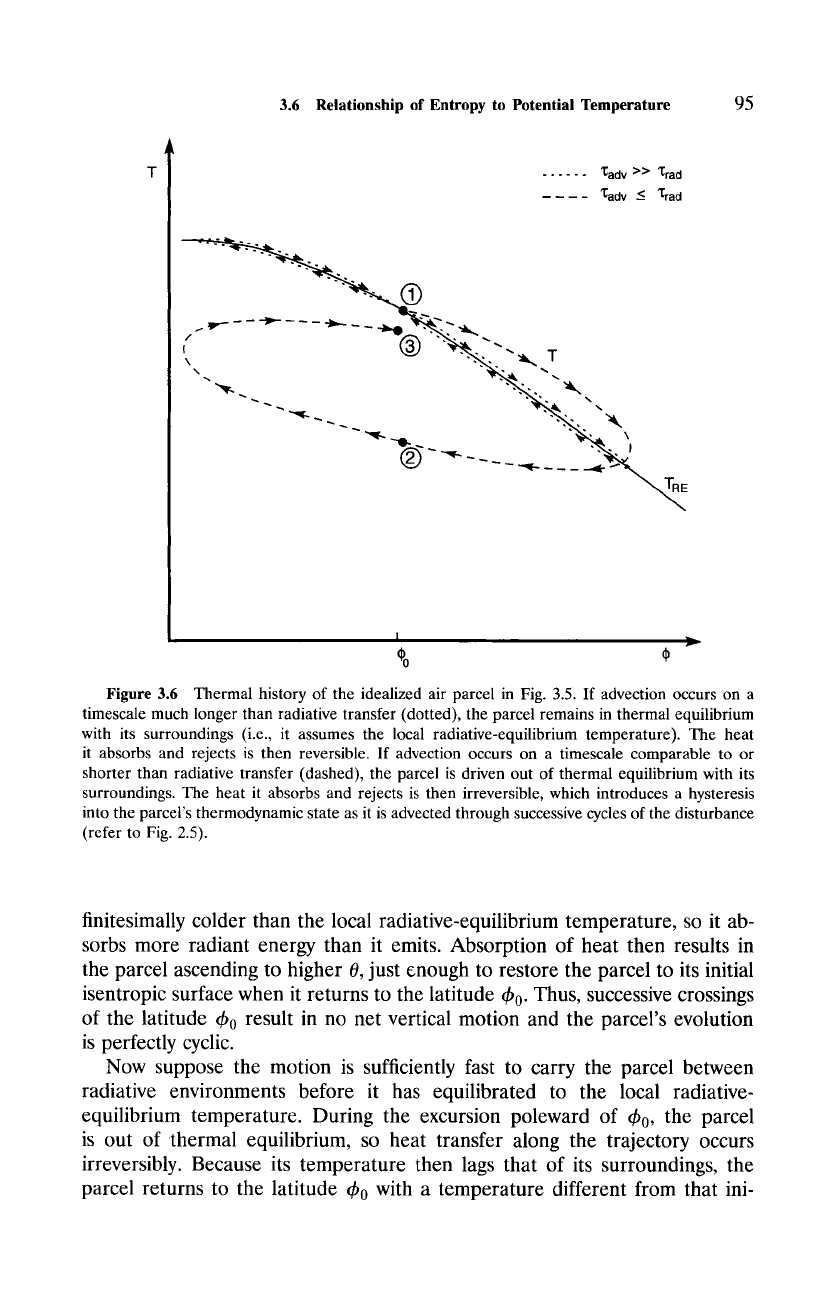
Suppose the displaced motion in Fig. 3.5 is sufficiently slow for the parcel

to equilibrate with its surroundings at each point along the trajectory. The

parcel's temperature then differs from TRZ only infinitesimally (Fig. 3.6), so the

parcel remains in thermal equilibrium and heat transfer along the trajectory

occurs reversibly. Between two successive crossings of the latitude ~b 0, the

The Second Law and Its Implications

O TRE Decreasing

q<O

>TRE

T<TF

*o @ | /

TRE(~

Figure 3.5 A wavy trajectory followed by an air parcel, which symbolizes the disturbed cir-

culations in Figs 1.9a and 1.10a. When displaced poleward, the parcel is warmer than the local

radiative-equilibrium temperature (contours), so it rejects heat. The reverse process occurs when

the parcel moves equatorward.

parcel absorbs heat such that

f2 f26q

(3.26)

cpd

0 - -~--.

If the heat exchange depends only on the parcel's temperature, for example,

6q = Tdf ( T),

which is symbolic of radiative transfer, then (3.26) reduces to

cpln(O-~11)-

Af- 0,

since Te = 7"1 =

TRe(~bo).

Thus,

0 2 "- 01

and the parcel is restored to its initial

thermodynamic state when it returns to latitude ~b 0.

While moving poleward, the parcel is infinitesimally warmer than the lo-

cal radiative-equilibrium temperature, so it emits more radiant energy than

it absorbs. Rejection of heat results in the parcel drifting off its initial isen-

tropic surface toward lower 0, which, for reasons developed in Chapter 7,

corresponds to lower altitude. While moving equatorward, the parcel is in-

3.6 Relationship of Entropy to Potential Temperature

=lp,~ _ _ ~ _ _ _ ..~. - ~'~

9 .-...,.,..

.....

~ "" "~r-~ ........

...... 1;ad v >> "l:;ra d

"lad v < 1;ra d

"" \1

Figure 3.6 Thermal history of the idealized air parcel in Fig. 3.5. If advection occurs on a

timescale much longer than radiative transfer (dotted), the parcel remains in thermal equilibrium

with its surroundings (i.e., it assumes the local radiative-equilibrium temperature). The heat

it absorbs and rejects is then reversible. If advection occurs on a timescale comparable to or

shorter than radiative transfer (dashed), the parcel is driven out of thermal equilibrium with its

surroundings. The heat it absorbs and rejects is then irreversible, which introduces a hysteresis

into the parcel's thermodynamic state as it is advected through successive cycles of the disturbance

(refer to Fig. 2.5).

finitesimally colder than the local radiative-equilibrium temperature, so it ab-

sorbs more radiant energy than it emits. Absorption of heat then results in

the parcel ascending to higher

just enough to restore the parcel to its initial

isentropic surface when it returns to the latitude ~b 0. Thus, successive crossings

of the latitude ~b 0 result in no net vertical motion and the parcel's evolution

is perfectly cyclic.

Now suppose the motion is sufficiently fast to carry the parcel between

radiative environments before it has equilibrated to the local radiative-

equilibrium temperature. During the excursion poleward of ~b 0, the parcel

is out of thermal equilibrium, so heat transfer along the trajectory occurs

irreversibly. Because its temperature then lags that of its surroundings, the

parcel returns to the latitude ~b 0 with a temperature different from that ini-

96 3

The Second Law and Its Implications

tially (Fig. 3.6). By the foregoing analysis, the parcel's potential temperature

02 also differs from that initially

Cp In (~)--Af #0,

since T2 ~ T1. Thus, the parcel is not restored to its initial isentropic surface,

but rather remains displaced vertically after returning to the latitude th0. Simi-

lar reasoning shows that heat transfer during the excursion equatorward of ~b0

(e.g., between positions 2 and 3 in Fig. 3.5) does not exactly cancel net heat

transfer during the poleward excursion. Hence, a complete cycle results in net

heat transfer and therefore a net vertical displacement of the parcel from its

initial isentropic surface.

Whether the parcel returns above or below that isentropic surface depends

on the radiative-equilibrium temperature and on details of the motion, which

control the history of heating and cooling. In either event, irreversible heat

transfer introduces a hysteresis (refer to Fig. 2.5), through which successive

cycles produce a vertical drift of air across isentropic surfaces. Because ad-

vection operates on a timescale much shorter than radiative transfer in the

atmosphere, disturbed horizontal motion invariably drives air out of thermal

equilibrium, introducing irreversible heat transfer, which in turn drives verti-

cal motion. Vertical motions generated in this fashion play an important role

in the mean meridional circulation of the atmosphere, which transfers heat,

moisture, and chemical constituents.

Suggested Reading

An illuminating treatment of the second law and its consequences to mechan-

ical and chemical systems is given in

The Principles of Chemical Equilibrium

(1971) by K. Denbigh.

Statistical Physics

(1980) by Landau

et al.

includes a clear discussion of re-

versibility and its implications for fluid systems.

Problems

3.1. Two hundred grams of mercury at 100~ is added to 100 g of water at

20~ If the specific heat capacities of water and mercury are 4.18 and

0.14 J kg-~K -1, respectively, determine (a) the limiting temperature of

the mixture, (b) the change of entropy for the mercury, (c) the change

of entropy for the water, and (d) the change of entropy for the system

as a whole.

3.2. For reasons developed in Chapter 9, many clouds are supercooled: They

contain droplets at temperatures below 0~ Consider 1 mol of super-

Problems

3.3.

3.4.

3.5.

3.6.

3.7.

3.8.

3.9.

cooled water in the metastable state: T = -10~ and p --- 1 atm. Fol-

lowing a perturbation, the water freezes spontaneously, with the ice and

its surroundings eventually returning to the original temperature. If the

heat capacities of water and ice remain approximately constant with the

values 75 and 38 J K -a mo1-1, respectively, and if the enthalpy of fusion

at 0~ is 6026 J mo1-1, calculate (a) the change of entropy for the water

and (b) the change of entropy for its environment.

Consider a parcel crossing isentropic surfaces. If radiative cooling is just

large enough to maintain the parcel on a fixed isobaric surface, what

is the relative change of its temperature when the parcel's potential

temperature has decreased to 90% of its original value?

Air moving inland from a cooler maritime region warms through con-

duction with the ground. If the temperature and potential temperature

increase by 5 and 6%, respectively, determine (a) the fractional change

of surface pressure between the parcel's initial and final positions and

(b) the heat absorbed by the parcel.

During a cloud-flee evening, LW heat transfer with the surface causes an

air parcel to descend from 900 to 910 mb and its entropy to decrease by

15 J kg -1 K -1. If its initial temperature is 280 K, determine the parcel's

(a) final temperature and (b) final potential temperature.

Derive expression (3.20) for the noncompensated heat transfer.

Air initially at 20~ and 1 atm is allowed to expand freely into an evacu-

ated chamber to assume twice its original volume. Calculate the change

of specific entropy.

(Hint:

How much work is performed by the air?)

The thermodynamic state of an air parcel is represented conveniently

on the

pseudo-adiabatic chart

(Chapter 5), which displays altitude in

terms of the variable pK. Show that the work performed during a cyclic

process equals the area circumscribed by that process in the

O-p ~

plane.

One mole of water at 0~ and 1 atm is transformed into vapor at 200~

and 3 atm. If the enthalpy of vaporization for water is 4.06

• 10 4

J mo1-1

and if the specific heat of vapor is approximated by

= 8.8- 1.9

• 10-3T

-t- 2.2

• 10-6T 2

cal

K -lmO1-1,

calculate the change of (a) entropy and (b) enthalpy.

3.10. The Helmholtz and Gibbs functions are referred to as

free energies

thermodynamic potentials.

Use the definitions (3.15) together with the

first and second laws for a closed system to show that (a) under isother-

mal conditions, the decrease of Helmholtz function describes the maxi-

The Second

Law and

Its Implications

mum total work which can be performed by the system:

Wma x ~ --Af,

(b)

under isothermal-isobaric conditions, the decrease of Gibbs function

describes the maximum work--exdusive of expansion work, which can

be performed by the system:

' - -Ag,

Wmax

where 8w' = 8w- pdv.

Chapter 4 Heterogeneous Systems

The thermodynamic principles developed in Chapters 2 and 3 apply to

a homogeneous system, which can involve only a single phase. For it to be

in thermodynamic equilibrium, a homogeneous system must be in thermal

equilibrium: at most an infinitesimal temperature difference exists between

the system and its environment, and also in mechanical equilibrium: at most

an infinitesimal pressure difference exists between it and its environment. A

heterogeneous system can involve more than one phase and, for it, thermo-

dynamic equilibrium requires an additional criterion. The system must also

be in

chemical equilibrium:

No conversion of mass occurs from one phase to

another. Analogous to thermal and mechanical equilibrium, chemical equilib-

rium requires a certain state variable to have virtually no difference between

the phases present.

4.1 Description of a Heterogeneous System

For a homogeneous system, two intensive properties describe the thermody-

namic state. Conversely, only two state variables may be varied independently,

so a homogeneous system has two thermodynamic degrees of freedom. For a

heterogeneous system, each phase may be regarded as a homogeneous sub-

system, one that is "open" due to exchanges with the other phases present.

Consequently, the number of intensive properties that describes the thermody-

namic state of a heterogeneous system is proportional to the number of phases

present. Were they independent, those properties would constitute additional

degrees of freedom for a heterogeneous system. However, thermodynamic

equilibrium between phases introduces additional constraints that actually re-

duce the degrees of freedom of a heterogeneous system below those of a

homogeneous system.

The system we consider is a two-component mixture of dry air and water,

with the latter existing

vapor I and possibly one condensed phase (Fig. 4.1).

This heterogeneous system is described conveniently in terms of extensive

1The

term vapor denotes water in gas phase and should not be confused with aerosol or other

forms of condensate.