Schlick T. Molecular Modeling and Simulation: An Interdisciplinary Guide

Подождите немного. Документ загружается.

300 10. Nonbonded Computations

Chapter 10 Notation Table (continued)

YMBOL DEFINITION

dv, dv

∗

volume elements

protonic charge

scattering amplitude for atom j

integer, level of reﬁnement in multipole expansion

particle mass

zeroth moment of Φ

components of dipole moment μ of Φ

, ···,m

components of quadrupole moment of Φ

integers

integer (power of expansion)

Coulomb partial charge for atom j

r, r

interatomic distance

{r, θ, φ}

spherical coordinates

u(x)

gravitational potential function

Lennard-Jones coefﬁcients for atom pair i, j (attraction,

repulsion)

coefﬁcients for modiﬁed Lennard-Jones potential

translational diffusion constant

coul

Coulomb potential

Lennard-Jones potential

nonbonded potential

scattered amplitude of whole crystal

gravitational constant

coul

Coulomb potential constant

box size dimension

} moments of the multipole expansion

number of variables (atoms)

Avogadro’s number

} Associated Legendre polynomials of degree n

earth’s radius

Squared interatomic distance (between atoms i and j),

)

S(r) shift/switch function

temperature

volume of unit cell (associated with volume element dv)

∗

volume of reciprocal space (associated with volume

element dv

∗

)

(θ, φ)} spherical harmonics functions

α, β, γ

angles

Gaussian screening parameter

Langevin damping constant



dielectric constant

(x)

position-dependent dielectric function



acc

desired accuracy

solvent viscosity

Debye screening parameter

ρ(x)

electron (or charge) density

screening Gaussian

φ(s)

phase angle associated with structure factor F

weight

10.1. A Computational Bottleneck 301

Chapter 10 Notation Table (continued)

YMBOL DEFINITION

Φ electrostatic potential

real

real (or direct-space) component of Φ

recip

reciprocal-space component of Φ

cor,ex

correction term for excluded nonbonded interactions

cor,self

correction term for self nonbonded interactions

cor,

correction term for ﬁnite dielectric

Hofstadter’s law: It always takes longer than you expect, even when

you take into account Hofstadter’s law.

Douglas R. Hofstadter, in Godel, Escher, Bach, 1979 (1945–).

10.1 A Computational Bottleneck

Reducing the cost of the nonbonded energy and force computations is of primary

importance in molecular mechanics and dynamics simulations of biomolecules.

This is because the direct evaluation of these nonbonded interactions involving all

atom pairs has the complexity of O(N

) where N is the number of atoms. Recall

that the bonded terms are local and thus have a linear computational complexity;

see homework assignment 8 for a related exercise.

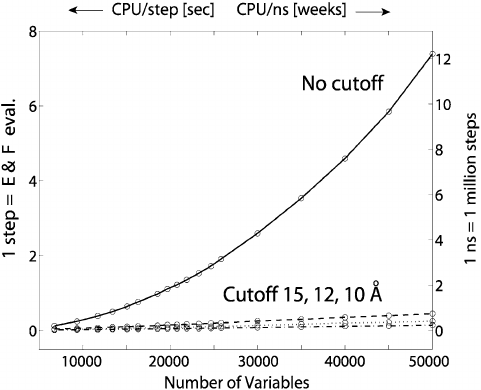
The rapid, quadratic growth in CPU time when all nonbonded interactions

are summed directly versus the linear growth associated with the “cutoff” pro-

cedures (consideration of interactions within a limited distance range) is shown in

Figure 10.1; see CPU scale at left for the evaluation of an energy and force. The

implication of these CPU times on total times for 1 ns trajectories (of one million

steps) is also shown (see scale at right), explaining the urgency in reducing the

nonbonded-term evaluation cost.

The data in Figure 10.1 and Table 10.1 show, for example, that computing all

the nonbonded energy and force interactions directly for a hen egg-white (HEW)

lysozyme protein (1960 atoms or 5880 Cartesian variables) in vacuum requires

about 0.18 seconds on a single Intel Xeon/3GHz processor of a Dell Linux ma-

chine. One million such steps to span one nanosecond by molecular dynamics

with a 1 femtosecond timestep would require approximately 1.4 days. A system

that is seven times larger (e.g., size range of a small solvated protein) requires

roughly a factor of 45 more computational time, or nearly 62 days of CPU to span

a single nanosecond!

Fortunately, techniques have been developed to reduce this cost dramatically

without destroying the value of simulations of biomolecules in solvent.

302 10. Nonbonded Computations

Figure 10.1. CPU time per step (energy plus force evaluation) for water clusters of various

sizes modeled in CHARMM when cutoffs are used (at 10, 12, and 15

A) versus no cutoffs

(see left vertical scale) by direct calculation, and corresponding times required for 1 ns tra-

jectories assuming 10

steps of 1 fs (see right vertical scale). The number of variables is

nine times the number of water molecules. Timings were obtained on a single Xeon/3GHz

processor of a Dell Linux machine.

This chapter introduces novice modelers to three fundamental techniques for

handling the nonbonded interactions of large biomolecular systems: spherical cut-

offs, particle-mesh Ewald, and fast multipole schemes. We conclude with a brief

mention of alternative continuum solvent models, such as Langevin and Brownian

dynamics and Poisson-Boltzmann calculations.

10.2 Approaches for Reducing Computational Cost

10.2.1 Simple Cutoff Schemes

The spherical cutoff techniques introduced in the next section are easy to im-

plement as well as computationally cheap (O(N )). More sophisticated than

straightforward truncation, these methods can yield reasonable approximations

to the energy and force functions up to some threshold separation-distance value.

They are particularly suitable for van der Waals interactions which decay rapidly

with distance and therefore can be considered zero beyond some interatomic

separation distance. Spherical cutoff methods have been used by necessity for

simulations of large systems

10.2. Approaches for Reducing Computational Cost 303

Table 10.1. Computational requirements of nonbonded calculations on CHARMM version

28a2 by cutoffs, direct nonbonded computations (‘all nonbonded’), or all nonbonded by

particle-mesh Ewald (PME).

Model

Atoms/ CPU/step

CPU/ns

Var iabl es [sec.] [days]

HEW Lysozyme, 12

A cutoffs 1960/ 0.03 0.29

HEW Lysozyme, all nonbonded 5880 0.18 1.38

Solvated DNA, 12

A cutoffs 12389/ 0.26 3.08

Solvated DNA, PBC, 12

A cutoffs 37167 0.63 7.35

Solvated DNA, all nonbonded 4.04 46.83

Solvated BPTI, 12

A cutoffs 14275/ 0.30 3.49

Solvated BPTI, PBC, 12

A cutoffs 42825 0.76 8.82

Solvated BPTI, PBC/PME 0.83 9.65

Solvated BPTI, all nonbonded 5.35 61.91

(For lysozyme): nonbonded cutoffs via group-based electrostatic switch and atom-based

Lennard-Jones switch functions, switch buffer 10 to 12

A, pairlist buffer 12 to 13

A, and SHAKE

used for all bonds involving hydrogens.

(For DNA dodecamer and BPTI): nonbonded cutoffs with periodic boundary conditions (PBC) via

atom-based electrostatic and Lennard-Jones switch functions, switch buffer 10 to 12

A, pairlist buffer

12 to 13

A, and SHAKE used for all bonds involving hydrogens.

Each step entails an energy and gradient evaluation performed in the CHARMM program. The

timings were made on a single Intel Xeon/3GHz processor of a Dell Linux machine.

We assume 1 fs timesteps.

10.2.2 Ewald and Multipole Schemes

Of course, cutoff methods neglect long-range interactions beyond some distance

and therefore are poor approximations for highly charged systems where large-

scale conformational arrangements of linearly-distant residues are involved. The

alternative techniques mentioned in the following sections are more suitable for

these cases.

Approximating all nonbonded interactions can be accomplished by fast elec-

trostatic techniques based on multipole expansions or Ewald lattice techniques.

These schemes have revolutionized the biomolecular simulation ﬁeld in the past

decade since their computational complexity is only O(N log N), a dramatic

computational saving with respect to the direct value of O(N

For example, computing the energy and force using spherical cutoffs of

range 12

A for a solvated small protein (BPTI) of size 14275 atoms (42825

variables) modeled in a periodic domain requires about 0.76 seconds on a

Xeon/3GHz processor of a Dell Linux machine; one million such steps to span

one nanosecond by molecular dynamics with a 1 fs timestep would require about

9 days. If all Coulomb interactions for the same system are computed with the

304 10. Nonbonded Computations

particle-mesh Ewald technique available in CHARMM, the computing time per

step (and nanosecond) would increase slightly (but of course accuracy will in-

crease; see Table 10.1). In comparison, direct evaluation of all nonbonded terms

would make the project untenable!

An efﬁcient three-dimensional version of the fast multipole method is rather

involved to implement; this might explain the preference to date for Ewald tech-

niques in the biological simulation community. The Ewald approach is applied

to periodic domains, and this has been known to produce nonphysical long-range

correlations for the system [510,580,581,1203]. These effects may, however, be

considered secondary in general in comparison with truncation artifacts.

Such problems remind practitioners that rarely in the ﬁeld of biomolecular sim-

ulations are pure gains involved due to improving methodologies; there is often

a balance between the approximations made and the physical reality of the re-

sulting models. See [1081] for an overview of Ewald and multipole methods for

computing long-range electrostatic effects in biomolecular dynamics simulations.

Before we introduce the Ewald and fast multipole techniques, we present

spherical cutoff methods. Continuum solvation models based on the Poisson-

Boltzmann equation are also discussed at the end of this chapter.

The notation used in this chapter (e.g., lattice vectors, scattering factors),

though different from some other parts of this text, follows presentations elsewhere

on the Ewald summation; these conventions originated in the crystallographic

community and have been adopted by the molecular simulation community.

10.3 Spherical Cutoff Techniques

10.3.1 Technique Categories

There are three basic categories of cutoff techniques: truncation, switch,andshift

formulations. All approaches set the distance-dependent nonbonded function to

zero beyond some distance value r = b; however the functional values for r<b

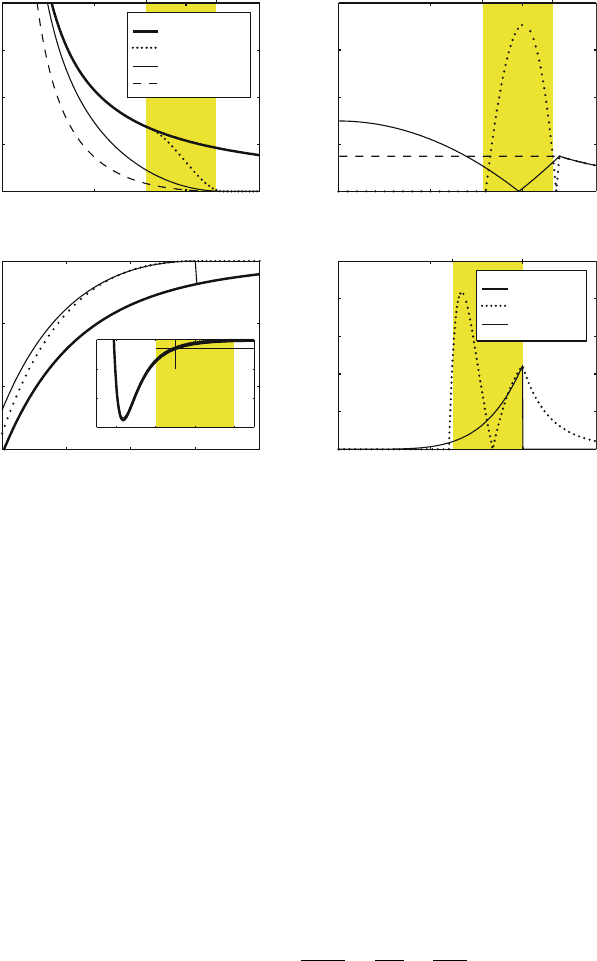
are treated differently (see Figure 10.2; the mathematical formulas mentioned in

the caption are discussed below):

• The simplest approach, truncation, abruptly deﬁnes values to be zero at b

and does not alter the values of the energies and forces for distances r<b.

• Switching schemes begin to change values at a nonzero value a<bbut

leave values for r<aunchanged.

• Shift functions alter the function more gradually for all r<b.

These three general categories can be applied to either the energy or the force

function of the nonbonded potential (van der Waals or electrostatic). When the

force rather than energy function is altered, the energy value is obtained by

integration.

10.3. Spherical Cutoff Techniques 305

In addition, atom-based or group-based schemes can be used. In the latter,

distance thresholds are applied to distances between group centers. Group-based

cutoffs can better maintain charges associated with entire residues. They can thus

avoid potential instabilities in the energy or force that arise when only a subset of

atoms of a particular residue is altered.

Besides choosing the particular approach (e.g., atom-based potential switch,

group-based force switch), care is required in specifying the distance parameters

a and b.

The cutoff techniques described here are also employed when multiple-

timestep integration schemes are applied to different force classes (see

Chapter 14); in these applications, force switching techniques are often used.

10.3.2 Guidelines for Cutoff Functions

In developing nonbonded cutoff functions, we are guided by the following

considerations.

1. The short-range energies and forces should be altered as minimally as

possible (while satisfying other criteria below).

2. The energies should be altered gradually rather than abruptly to avoid the

introduction of artiﬁcial minima (where the potential energy and gradient

values are suddenly zero).

3. The cutoff approach should avoid introducing large forces around the cutoff

region (spikes in right panels of Figure 10.2). This is especially important

for molecular dynamics simulations.

4. Also for molecular dynamics, it is important that the cutoff approach alters

the functions in a way to approximately conserve the energy.

Truncation schemes satisfy criterion 1 above but violate all others and are re-

moved from further consideration. Switching schemes alter the potential less than

shift schemes (since function values for r<aare not altered) but can introduce

artiﬁcial minima and large sudden forces (Fig. 10.2), violating criterion 3. Energy

conservation (criterion 4) can be problematic for certain group-based implemen-

tations when polar groups are involved near the cutoff region. Improved (force)

shift and force switch functions are often preferred for molecular dynamics ap-

plications [1220] with a sufﬁciently wide buffer region [a, b] (e.g., 8 to 12

Aor

11 to 15

A) and a large enough cutoff value b (≥12

A).

In general, the choice of the best spherical cutoff scheme to use depends on the

force ﬁeld and the system being studied. See [923] and references cited therein

for studies on the effect of different cutoff and long-range electrostatic models on

the stability and accuracy of biomolecular simulations.

306 10. Nonbonded Computations

a b

0 5 10

Orig.

Pot. SW

Pot. SH1

Pot. SH2

Elec. potential

a b

0 5 10

0.1

0.2

0.3

0.4

Elec. force error mag.

7 8 9 10 11

−6

−4

−2

x 10

−3

VdW potential

4 6 8 10

−0.06

−0.04

−0.02

a b

0 5 10

0.2

0.4

0.6

0.8

x 10

−3

VdW force error mag.

Orig.

Pot. SW

VdW SH

Figure 10.2. Various cutoff schemes — potential switch, eq. (10.4), and two types of poten-

tial shift, eqs. (10.10), (10.11) — with buffer regions of 8–12

A (electrostatic) and 6–10

(van der Waals). The altered potentials E(r) are shown on the left panels (a,c), and the cor-

responding errors in the associated forces (Δ|F

mod

− F

orig

|), reﬂecting the magnitude of

the difference between the original and modiﬁed force, are shown on the right panels (b,d).

The potential shift function for the van der Waals interaction corresponds to eq. (10.14).

Parameters from the CHARMM program are used, modeling a C

–C

interaction in pep-

tides. The corresponding charge for this atom type is −0.18 esu, and the van der Waals

parameters {

} are −0.055 kcal/mol and 2.175

A, respectively (see eqs. (9.36), (9.37)

of Chapter 9 for deriving V

and r

), producing: A

= 745.295 [kcal/mol]

and

=2.525 × 10

[kcal/mol]

; the values of C

and D

from eqs. (10.15)and

(10.16)areC

= −7.403 × 10

−10

[kcal/mol] /

and D

= −0.0015 kcal/mol.

10.3.3 General Cutoff Formulations

Consider the following general modiﬁcation to the nonbonded energy function

by a distance-dependent switch or shift function S(r):

(X)=



i,j

S(r

)



−A

r



. (10.1)

Here X is the collective position vector, r

represents the distance between atoms

i and j, and the parameters 0 ≤ ω

≤ 1 are weights. These weights can be

10.3. Spherical Cutoff Techniques 307

used to exclude bonded terms (i.e., 1–2 interactions) or bond-angle interactions

(1–3) (i.e., with ω

=0), or to scale other interactions such as those involving a

sequence of four bonded atoms (1–4).

Truncation

Simple truncation can be expressed by the switch function S deﬁned as

S(r)=



1 r<b

0 r ≥ b

. (10.2)

This function introduces a force discontinuity at r = b and fails to conserve en-

ergy. In general, S(r) is a distance-dependent distance function which assigns a

constant value or a function of r depending on the value of r with respect to the

distance parameters a and b. Thus S(r) may be set separately for the three cases:

r ≤ a, a<r≤ b,andr>b.

Switch/Shift

The switch/shift function can be different for the van der Waals and electrostatic

terms; in that case eq. (10.1) should be written as two terms with different func-

tions S(r). The CHARMM program, for example, uses the same switch functions

for both van der Waals and Coulomb interactions but different shift functions for

these terms when selected.

Atoms/Groups

The above formulation is atom-based. Group-based formulations apply the

distance-dependent switch/shift functions based on the separation of group

centers. For example, if such an intergroup distance is in the buffer region [a, b],

the modiﬁcation that S applies in this range (see below) is used for all atoms in

the two groups; similarly, this intergroup distance determines the modiﬁcations

applied to all atoms in the two groups when the distance falls in the other two

regions: r<aand r>b.

Energy/Force Modiﬁcations

When a modiﬁcation is applied to the force F

instead of the potential en-

ergy of the nonbonded terms, each r

-dependent force term, namely F

is modiﬁed as:



)=ω

S(r

) F

) (10.3)

where the force rather than the potential is switched by the operator S(r).The

corresponding energy must then be obtained by integration.

10.3.4 Potential Switch

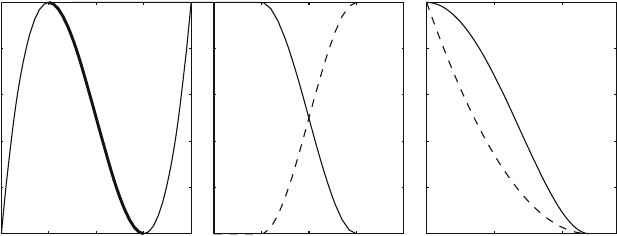
For potential switch functions, S(r) is a polynomial of r that alters the nonbonded

energy smoothly and gradually over the buffer region [a, b] so that E(b)=0,

308 10. Nonbonded Computations

while leaving values of the energy function E(r) for r ≤a unchanged. The poly-

nomial degree must be sufﬁciently high to ensure that both the energy and its

gradient are continuous functions. A satisfactory function is the following cubic

polynomial of r

(see Figure 10.3, part (a)):

S(r)=

⎧

⎨

⎩

1 r<a

1+y(r)

[2y(r) − 3] a ≤ r ≤ b

0 r>b

, (10.4)

where

y(r)=(r

− a

)/(b

− a

) . (10.5)

The S(r) expression above for a ≤ r ≤ b can also be written as (following

algebra):

S(r)=

− r

)

+2r

− 3a

)

− a

)

for a ≤ r ≤ b. (10.6)

From this form, it is clear that S(r) decreases monotonically from 1 to 0 as r

increases from a [y(a)=0and S(a)=1]tob [y(b)=1and S(b)=0]. Note

that for a<r<bthe derivative from eq. (10.6)is:



(r)=12ry(r)[y(r) − 1]/(b

− a

) , (10.7)

and thus both the right derivative of S(r) at a and the left derivative of S(r) at

b (where y(r)=0and 1, respectively) are zero. Since these derivatives are also

zero from the left of a and the right of b (where S(r) is a constant function), both

the potential and the gradient functions are continuous. This function S(r) also

yields continuous second derivatives when the force, rather than the energy, is

switched on or off.

10.3.5 Force Switch

Rather than switching the potential, force switching is used in multiple-timestep

schemes to gradually separate the short from long-range forces.

Often, force

classes are deﬁned according to a distance parameter b closely related to the cutoff

distance above. For example, interactions within a region of b

A can be considered

‘fast’ and those beyond that value ‘slow’ (e.g., b =6

A). In this case, the short-

range forces are turned off gradually by a switch function S(r) that decreases

from 1 to zero as r increases from a to b in a manner closely resembling that of

S deﬁned in eq. (10.4). Here the region [a, b] is the switching buffer region, and

c = b −a is the size of this buffer.

These two components are also termed ‘fast’ and ‘slow’ because the short-range terms are

rapidly varying in time while the long-range terms change more slowly with time; see Chapter 14.

10.3. Spherical Cutoff Techniques 309

−0.5 0 0.5 1 1.5

0.2

0.4

0.6

0.8

y(r)

Switch

S[y(r)]

6 8 10 12 14

S(r)

1−S(r)

MTS

Switch

0 5 10

(r)

Shift

S(r)

abc

Figure 10.3. Switch and shift functions: (a) the potential switch function of eq. (10.4)as

a function of y(r) given in eq. (10.5); only the heavier part of the curve is relevant since

y(r) increases from 0 to 1 as r increases from a to b; (b) the switch function S(r) of

eq. (10.9) that is applied to the fast force component in multiple-timestep schemes (solid

curve), along with 1 − S(r) (dashed curve) that is applied to the slow force component

(see eq. (10.8)); (c) the shift functions S

(r) and S

(r) of eqs. (10.10)and(10.11).

The switching function is applied as follows to the fast and slow force

components of F

NB, fast

= S(r) F

(r)

NB, slow

=[1− S(r)] F

(r) , (10.8)

where the function S(r) is deﬁned as:

S(r)=

⎧

⎨

⎩

1 r<a

1+r

(2r − 3) a ≤ r ≤ b

0 r>b

. (10.9)

See Figure 10.3, part (b), for an illustration.

Buffer Parameters

In addition to the buffer length c (which can range from 1 to 4

A, for example),

another buffer parameter c is typically used for bookkeeping purposes. Namely,

to keep track of the nonbonded atom pairs {i, j} used to associate each pair of

atoms with a force term in which it is calculated (i.e., fast or slow), the pairlist is

monitoreduptoadistanceb +c. Implementations vary from program to program,

but the main idea is to use this buffer size c to monitor changes in interatomic

distances that would require a new pairlist generation (see [1025] for example).

10.3.6 Shift Functions

Shift-type functions can avoid the sudden changes in force that occur with trun-

cation and switch methods at the cost of underestimating the short-range forces