Schlick T. Molecular Modeling and Simulation: An Interdisciplinary Guide

Подождите немного. Документ загружается.

13.2. Laplace’s Vision of Newtonian Mechanics 431

Caption to Figure 13.1: (a) MD simulations of 7 single-residue variants at

residue Arg517 of a polymerase λ/DNA complex illustrate this residue’s im-

portance in stabilizing the complex, as evident by the wide residue-dependent

ﬂuctuations captured in dynamics simulations [413]. The DNA snapshots are

superimposed with respect to the active (green) and inactive (red) DNA po-

sitions. (b) BD snapshots of long DNA capture large-scale motions, such as

site-juxtaposition kinetics (see Box 6.7 of Chapter 6) of two segments located

900-bp along the DNA contour, in the millisecond timeframe [577]. (c) MC con-

ﬁgurations and ensemble radius of gyration/energy plot from a folding simulation

of 434-repressor protein show RMS values for predicted structures, superimposed

with native conformations [437]. (d) PB contours illustrate the electrostatic poten-

tial of mouse acetylcholinesterase (D. Sept, K. Tai, and J.A. McCammon, personal

communication, and see [356, 1253]). (e) TMD snapshots of polymerase β cap-

ture the large-scale conformational change of the enzyme from closed (red) to

open (green) forms [1408] shown here as reﬂected by motion of several residues

near the active site. (f) The minimized adduct of a DNA duplex with a carcinogen

(2-aminoﬂuorene) was computed with NMR constraints [969].

The celebrated French mathematician Pierre Simon de Laplace (1749–1827)

recognized the far-reaching implications of Newtonian physics almost two cen-

turies ago. In this now-classic piece, Laplace dreams about predicting the future,

as well as reproducing the past, by animating Nature’s forces (see Box 13.1)[290].

While stated in an era when the effect of high-speed computers on modern

life and science could hardly be imagined, Laplace’s vision already contains

the essential ingredients of present-day biomolecular simulations: mathematical

construction of the suitable force ﬁeld (forces), design of appropriate numerical

integration tools (analysis), and long-time propagation of the equations of motion

(far-reaching intelligence).

One hundred years later, the British theoretical physicist Paul Dirac (1933

Nobel Laureate in Physics with Erwin Schr¨odinger for pioneering contributions

in quantum physics), acknowledged that we now have formulations for Nature’s

forces but lamented that these equations are too complex to solve [320]:

The fundamental laws necessary for the mathematical treatment of a

large part of physics and the whole of chemistry are thus known, and

the difﬁculty lies only in the fact that application of these laws leads

to equations that are too complex to be solved.

Indeed, the energy landscape is complex for biomolecules [422, 1386, 1387].

The various contacts — be they hydrogen bonds, disulﬁde bonds, or noncovalent

interactions like stacking and favorable electrostatics — are difﬁcult to predict

apriori. Thus, the multidimensional potential energy surface that governs biomo-

lecular structure has many maxima, minima, and saddle points. The distributions

about each favorable or unfavorable state are highly anisotropic, with the width

depending on the entropy associated with that state.

432 13. Molecular Dynamics: Basics

Biomolecules are also asymmetric in comparison to simple systems, such as

homogeneous liquid clusters, which were successfully simulated much earlier.

Certainly, there are symmetries in many aspects of protein and nucleic acid struc-

ture (e.g., many proteins are dimers, and the “ideal” DNA double helix has an

axis of symmetry), but in realistic environments there are many sequence-speciﬁc

motifs and binding interactions

However, modern computers have overcome the limitation noted by Dirac,

allowing us to solve the complex equations!

13.2.2 Deterministic Mechanics

As Laplace stated, the capability to analyze and predict motion — be it of the

solar system or a biological system — provides the link between the past and

the future. Still, even Newtonian mechanics taken to its extreme cannot predict

with certainty the future motion of all bodies. As became evident by the work of

Poincar´e less than a century after Laplace’s statement, the solar system is chaotic

even though the underlying laws can be clearly expressed. This understanding,

however, should not deter us from pursuing Laplace’s dream; rather, it should

stimulate us to explore as deeply as possible the consequences of Newtonian

physics.

13.2.3 Neglect of Electronic Motion

In addition to the limitation of deterministic mechanics, only the nuclear motion

of many-body systems is typically followed in molecular dynamics. Thus, elec-

tronic motion is not considered, and quantum effects are generally ignored. The

classical approximation is excellent for a wide range of systems and materials but

is unsuitable for reactions involving electronic rearrangements such as bond for-

mation and cleavage, polarization, and chemical bonding of metal ions. Quantum

dynamical approaches are used for this purpose. They are, however, at a relatively

early stage with respect to macromolecular applications and are not covered in

this text.

Box 13.1: Laplace’s ‘Far-Reaching Intelligence’

Laplace, the son of a Normandy farmer, is famous for his masterpieces on Celestial Me-

chanics and the Theory of Probability [290]. The Laplace equation (though written by Euler

in 1752 in a hydrodynamic context) is Laplace’s chief contribution to potential theory. In

his 1820 oeuvre [290], Laplace states:

Une intelligence qui, pour un instant donn´e, connaˆıtrait toutes les forces dont

la nature est anim´ee et la situation respective des ˆetres qui la composent,

si d’ailleurs elle ´etait assez vaste pour soumettre ces donn´ees `a l’Analyse,

embrasserait dans la mˆeme formule les mouvements des plus grands corps

de l’univers et ceux du plus l´eger atome: rien ne serait incertain pour elle,

13.2. Laplace’s Vision of Newtonian Mechanics 433

et l’avenir, comme le pass´e, serait pr´esent `a ses yeux. L’esprit humain offre,

dans la perfection qu’il a su donner `a l’Astronomie, une faible esquisse de

cette intelligence.

An intelligence which could, at any moment, comprehend all the forces by

which nature is animated and the respective positions of the beings of which

it is composed, and moreover, if this intelligence were far-reaching enough

to subject these data to analysis, it would encompass in that formula both

the movements of the largest bodies in the universe and those of the lightest

atom: to it nothing would be uncertain, and the future, as well as the past,

would be present to its eyes. The human mind offers us, in the perfection

which it has given to astronomy, a faint sketch of this intelligence.

13.2.4 Critical Frequencies

Classical MD simulations are also unsuitable for low temperatures, where the en-

ergy gaps among the discrete levels of energy dictated by quantum physics are

much larger than thermal energy available to the system. This is because the sys-

tem is conﬁned to one or a few of the low-energy states under such conditions.

This discrete description of energy states becomes less important as the temper-

ature is increased and/or the frequencies associated with motion are decreased

(i.e., have longer timescales). Under those conditions, more energy states become

thermally accessible.

Rough estimates for the characteristic motions for which Newtonian physics

is reasonable can be made on the basis of harmonic analysis. For a harmonic

oscillator, the quantized energies are separated by hν where h is Planck’s constant

and ν is the vibrational frequency.

Clearly, the classical approach is unsuitable for capturing motions with

relatively high frequencies ν, that is with ν  k

T/h,or

hν

 1 , (13.1)

where k

is Boltzmann’s constant, and T is the temperature. This is because the

probability of ﬁnding the system with this mode at the ground state energy is high.

The larger this ratio, the greater this probability.

Conversely, classical behavior is approached for frequency/temperaturecombi-

nations for which

hν

 1 . (13.2)

Around the room temperature of 300 K, k

T=0.6 kcal/mol. As we see

from Table 13.2, the high-frequency vibrational modes present in biomolecules

434 13. Molecular Dynamics: Basics

Table 13.2. Ratios for some high-frequency vibrational modes at T = 300 K.

Wave number Frequency Ratio

Vibrational mode (1/λ)[cm

−1

] ν = c/λ [s

−1

] hν/(k

O–H stretch 3600 1.1 × 10

C–H stretch 3000 9.0 × 10

O–C–O asym. stretch 2400 7.2 ×10

C=O (carbonyl) stretch 1700 5.1 × 10

C–N stretch (amines) 1250 3.8 × 10

O–C–O bend 700 2.1 × 10

have ratios larger than unity. They are thus not well treated by classical physics.

Speciﬁcally, Newtonian physics, which distributes the energy equally among

all vibrational modes according to the equipartition theorem, overestimates the

energy/motions associated with these high-frequency modes.

The critical frequency ν for which equality of the above ratio holds is around

6.25 × 10

−1

or 6 ps

−1

, corresponding to an absorption wavelength of

208 cm

−1

(or period of 160 fs). Thus, modes with characteristic timescales in

the picosecond and longer timeframes are reasonably treated by classical, Newto-

nian physics. The second and third classes of motions identiﬁed for biomolecules

in Table 13.3 fall in this range.

Table 13.3. The broad spectrum of characteristic timescales in biomolecules.

Internal Motion Timescale

[seconds]

Light-atom bond stretch 10

−14

Double-bond stretch 2 × 10

−14

Light-atom angle bend 2 ×10

−14

Heavy-atom bond stretch 3 × 10

−14

Heavy-atom angle bend 5 × 10

−14

Global DNA twisting 10

−12

Sugar puckering (nucleic acids) 10

−12

–10

−9

Collective subgroup motion (e.g., hinge bending,

allosteric transitions) 10

−11

–10

−7

Surface-sidechain rotation (proteins) 10

−11

–10

−10

Global DNA bending 10

−10

–10

−7

Site-juxtaposition (superhelical DNA) 10

−6

–1

Interior-sidechain rotation (proteins) 10

−4

–1

Protein folding 10

−5

–10

13.3. The Basics: An Overview 435

13.2.5 Hybrid Quantum/Classical Mechanics Treatments

Electronic motions which have much higher characteristic frequencies must be

treated by alternative approaches such as quantum-mechanical and hybrid quan-

tum/classical approximations; excellent progress has been made in recent years

on these techniques as discussed in a previous chapter [75, 270, 441, 452, 572–

574, 628, 1163–1165, 1342, 1348, 1442]. Essentially, in these approaches, the

reacting part of the system (e.g., active site of an enzyme) is treated quantum

mechanically, while the other components (e.g., remaining amino acids and sol-

vent) are modeled classically, by molecular mechanics, as ﬁrst proposed in the late

1970s [1344]. Such treatments are critical for calculating reaction pathways and

intermediates for bond-breaking events, reaction rates for formation of organic

compounds in solution, or free energies of hydration. They are also necessary

for describing localized enzymatic activity entailing charge transfer, or solvent

polarization effects. Important recent progress in this area was mentioned in

Chapter 8. Still, many technical details must be perfected regarding these more

complex simulation protocols. For example, challenging are the proper deﬁnition

of the quantum-mechanical treatment and the merging between the quantum and

classical approximations and the proper sampling involved to compute accurate

reaction rates.

Besides resorting to QM/MM techniques, many innovative sampling methods

have now been developed that can estimate reaction mechanisms and rates for

conformational pathways. These are mentioned in the end of the next chapter.

13.3 The Basics: An Overview

13.3.1 Following the Equations of Motion

The molecular dynamics approach is simple in principle. We simulate motion of

a system under the inﬂuence of a speciﬁed force ﬁeld by following molecular

conﬁgurations in time according to Newton’s equation of motion. We write these

equations for a system of N atoms as the following pair of ﬁrst-order differential

equations:

V (t)=F (X)=−∇E(X(t)) + ... ,

X(t)=V (t) . (13.3)

In these equations, X ∈ RI

denotes the collective Cartesian vector of the sys-

tem (i.e., the x, y,andz components of each atom are listed in turn); V is the

corresponding collective velocity vector; M is the diagonal mass matrix (i.e., the

masses of each atom are repeated three times in the diagonal array of length 3N);

and the dot superscripts denote differentiation with respect to time, t.

The total force F in the right-hand-side of eq. (13.3) is composed of the system-

atic force, which is the negative gradient (vector of ﬁrst partial derivatives) of the

potential energy E and, possibly, additional terms that mimic the environment.

436 13. Molecular Dynamics: Basics

(See section 14.4 on stochastic dynamics for an example of these additional

terms). Each gradient component i, i =1,...3N, is given by:

∇E(X)

= ∂E(X)/∂α

where α

denotes an x, y,orz component of an atom. These equations must be

integrated numerically since analytic (closed-form) solutions are only known for

the simplest systems. Such numerical integration generates a sequence of posi-

tions and velocity pairs, {X

}, for integers n that represent discrete times

t = nΔt at intervals (timesteps) Δt.

13.3.2 Perspective on MD Trajectories

Force Field Dependency

Results of a molecular dynamics simulation can only be as good as the governing

force ﬁeld. Essentially, the mechanical representation of a system — particles

connected by springs — assumes simple, pairwise-additive potentials. These

express how the composite atoms stretch, vibrate, and rotate about the bonds in re-

sponse to intramolecular and intermolecular forces. The resultant potential energy

E, as described in Chapters 9 and 10, is still highly approximate for biomolecules

and undergoes continuous improvements. Uncertainties are well recognized in the

representation of solvent [1099], polarization effects [510], and electrostatic in-

teractions [455, 668], and in the functional form of the local potentials (i.e., lack

of anharmonic [826] and cross terms [300]).

Statics Vs. Dynamics

Minimization of this approximate energy function yields information on favorable

regions in conﬁguration space (this approach is termed molecular mechanics or

statics). The numerical integration of the differential equations of motion reveals

the intrinsic motions of the system under the inﬂuence of the associated force

ﬁeld. Thus, in principle, MD simulations can combine both the spatial and tem-

poral aspects of conformational sampling. They are thus used in many cases as

conformational search tools — to bypass the multiple-minimum problem — and

as vehicles to reﬁne low-resolution X-ray or NMR (nuclear magnetic resonance)

data (e.g., [676]). However, for this purpose, special strategies, such as energy

modiﬁcations or high-temperature settings, are required if substantial movements

are desired. This is because MD simulations are severely limited by the very small

timesteps that must be used relative to the timescales of major biological interest.

Range of Timescales

Indeed, the motion of biomolecules involves an extraordinary range of timescales

(see Table 13.3). In general, the higher frequencies have smaller associated am-

plitude displacements. For example, while bond vibrations have characteristic

13.3. The Basics: An Overview 437

amplitudes of a tenth of an

Angstrom, global deformations can be in the order

of 100

A(seeTableIin[178] for classes of timescales and associated amplitudes

in biomolecular motions). The energies associated with these motions also span a

large range.

Though the fastest, high-frequency modes have the smallest amplitudes, these

motions affect other modes and thus their effect must be approximated in some

way. Yet, the existence of high-frequency modes severely affects the timestep that

can successfully be used in biomolecular simulations. Their timescale dictates

a timestep of 1 fs or less in standard explicit schemes for acceptable resolution

(a tenth or less of a period). This stepsize already implies one million steps to

cover only a nanosecond and falls short, by more than ten orders of magnitude,

of the slow and large-amplitude processes of major biological interest. Dealing

with this severe timestep problem has been the focus of many research groups,

and some results will be the subject of sections that follow.

Challenges

Thus, in summary, although the basic idea is simple, the art of MD simulations is

challenging in practice. The practical difﬁculties arise from various components

that enter into biomolecular simulations: setting initial conditions, implement-

ing various simulation protocols to ensure reliability, using suitable numerical

integrators, considering the sensitivity of trajectories to initial conditions and

other choices, meeting the large computational requirements, and visualizing and

analyzing the voluminous data that are generated.

13.3.3 Initial System Settings

A molecular dynamics trajectory consists of three essential parts: initialization,

equilibration, and production. Initialization requires specifying the initial coordi-

nates and velocities for the solute macromolecule, as well as for the solvent and

ion atoms.

Structure

Even when initial coordinates are available from experiment (e.g., crystal struc-

ture), the starting vector may not correspond to a minimum in the potential energy

function used, and hence minimization (further reﬁnement) is needed to relax

strained contacts. When an experimental structure is not available, a build-up

technique may be used to construct a structure on the basis of the known building

blocks, and minimization again is required.

Solvation

When water molecules and salt ions are also used, special care is needed to carve

an appropriate solvation model around the biopolymer. The water coordinates

438 13. Molecular Dynamics: Basics

are typically taken from a pure water simulation (which reproduces the ex-

perimentally determined density), with initial ion placement guided by the

biopolymer charge distribution and experimental measurements. Special itera-

tive ion-placement algorithms are available in molecular dynamics programs that

place positive ions in electronegative pockets and negative ions in positively-

charged cavities so as to achieve a desired total ionic concentration. The ﬁnal

model is constructed following appropriate superimpositioning, removal of over-

lapping atoms, and energy relaxation. See [1419,1421], for example, for detailed

descriptions of such equilibration procedures for B-DNA and in [525, 526]

for RNA.

Velocity

The initial velocity vector is typically set pseudorandomly so that the total kinetic

energy of the system, E

, corresponds to the expected value at the target temper-

ature T. According to the classical equipartition theorem, each normal mode has

T)/2 energy, on average, at thermal equilibrium. Thus

E

 =



i=1

≡

)

M(V

)=(N

T)/2 , (13.4)

where N

is the total number of degrees of freedom in the system (3N or 3N −3;

see below).

Such a velocity setting can be accomplished by assigning velocity components

from a Gaussian distribution. Namely, each component v

can be chosen from a

Gaussian distribution with zero mean and a variance of (k

T)/m

. This implies

that v

 =(k

T)/m

, where the bracket · denotes the expected value. Utilities

to generate such distributions are based on uniform pseudorandom number gen-

erators and are available in many software packages (see discussion in the Monte

Carlo chapter).

According to the Central Limit theorem (see Chapter 12), the sum of inde-

pendent random variates, each chosen from a normal distribution, has itself a

normal density with a mean and variance that are simply the sum of the individ-

ual means and variances. Thus, the expected value of E

will correspond to the

target temperature:

E

 =





i=1

 =3N (k

T)/2 . (13.5)

Often, the three translational degrees of freedom are removed by modifying

the initial velocity vector so that the initial momentum is zero. This is done

by subtracting from each component of V

the center of mass velocity, v



,wherei =1,...,N). This modiﬁcation leaves the

ﬁnal temperature, measured with N

=3N − 3, unchanged.

13.3. The Basics: An Overview 439

Equilibration

Once the system is set and initial coordinates and velocities are assigned, an initial

round of equilibration is necessary before the production phase of the simulation

can begin. In this equilibration period, there is an exchange between kinetic and

potential energies. Stability is evident when both terms, and the total energy, ap-

pear to converge, with ﬂuctuations occurring about the mean value. This is the

expected behavior from a microcanonical ensemble (ﬁxed total energy, volume,

and particle number, or NVE for short); see Chapter 12, Subsection 12.5.3 and

Section 13.6.

Illustration

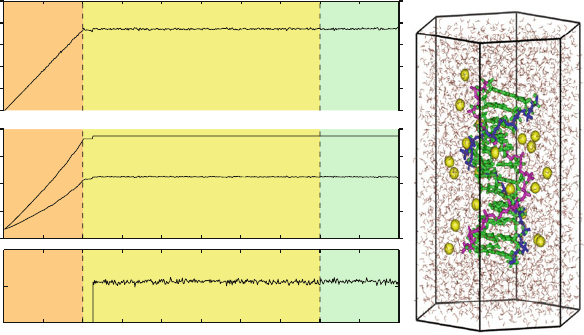
Figure 13.2 illustrates the convergence phase of a simulation, as obtained for a

hydrated DNA dodecamer system (12389 atoms: 760 of DNA, 22 sodium, and

3869 water molecules). A heating phase of 15,000 steps (5000 steps, 3

Kper

every 50 steps) ﬁrst brings the system to the target temperature. Note that dur-

ing the equilibration phase the potential and kinetic energies ﬂuctuate and the

total energy remains nearly constant (see enlargement at bottom). Second, the

leapfrog Verlet integrator (see later in chapter) with a timestep of 2 fs is applied,

in combination with bond-length restraints (see below), to all water molecules.

The water model consists of a periodic hexagonal-prism system of height 65

andsidelengthof26

A. In general, the equilibration time is system and protocol

dependent. A stochastic approach such as Langevin dynamics (as introduced in

Subsection 10.6.3 of Chapter 10) can simplify this equilibration task because the

random forces quickly lead the system to thermal equilibrium, even with a zero

initial velocity vector.

0.0

1.0

Heating Equilibration Production

−5.5

−3.5

Energy (kcal*10

/mol)

0 5 10 15 20 25 30 35 40 45 50

−3.630

−3.628

−3.626

Time (ps)

E, enlarged view

Figure 13.2. Heating and equilibration of a hydrated DNA dodecamer system of 12389

atoms in a hexagonal-prism periodic domain.

440 13. Molecular Dynamics: Basics

13.3.4 Sensitivity to Initial Conditions and Other Computational

Choices

The chaotic nature of individual MD trajectories is well appreciated. It is espe-

cially important to keep this aspect in mind when analyzing data for complex,

many-body systems. Roughly speaking, chaotic behavior means that a small

change in initial conditions (e.g., a fraction of an

Angstrom difference in Cartesian

coordinates) can lead to exponentially-diverging trajectories in a relatively short

time. The larger the initial differenceand/or the timestep, the more rapid this Lya-

punov instability [849].

Though chaos is a feature of the analytical equations

themselves, the ﬁnite arithmetic used by computers and the discretization errors

of the integrators used to simulate the trajectory are other factors that produce

divergence.

Chaos and Saturation

Figure 13.3 illustrates this sensitivity to initial conditions. Shown are the root-

mean-square (RMS) differences in atomic coordinates as a function of time t for

a water tetramer system:

e(t)=





i=1

(t) − x



(t))



1/2

; (13.6)

here, the coordinate of the perturbed trajectory is distinguished from the reference

trajectory by the prime superscript.

For each curve shown in the ﬁgure, the initial coordinates of the second trajec-

tory were perturbed by ± from the reference trajectory ( =10

−8

, 10

−6

, 10

−4

The velocity Verlet algorithm (see below) used timesteps of 0.1 fs and 1 fs, and

the difference e(t) is plotted every 20 fs, reﬂecting the average over that interval.

Several interesting features can be gleaned from this ﬁgure. A short period of

rapid exponential divergence is evident, followed by linear oscillations around

a threshold value. The ‘chaos’ often mentioned in MD texts refers to the initial

period of exponential growth. This is in fact local instability [849]. It is well

known from chaos theory that compact systems, like biomolecules, whose phase

space is ﬁnite, reach saturation for the trajectory error when the magnitude of the

deviations corresponds to a system-dependent value.

In other words, the phase trajectories cannot be found beyond the distance char-

acteristic of the phase space. As the plots show, the smaller the initial perturbation

(), the longer the time required to reach saturation. The same threshold is reached

for both timestep values.

Lyapunov exponents are related to the eigenvalues of the Jacobian of the transformation asso-

ciated with a dynamical system; they describe the rate of growth of an instability. For example, a

system that possesses local instability has a direction along which the distance between two points

in phase space at time t, |δ(t)|, grows exponentially at the rate λ

, the largest Lyapunov exponent:

|δ(t)| = |δ(0)|exp(λ

t).