Schlick T. Molecular Modeling and Simulation: An Interdisciplinary Guide

Подождите немного. Документ загружается.

13.3. The Basics: An Overview 441

0 5 10 15 20

Time (ps)

Δτ = 1 fs

ε = ±

0 5 10 15 20

−8

−7

−6

−5

−4

−3

−1

−2

−8

−7

−6

−5

−4

−3

−1

−2

Time (ps)

RMS coordinate deviation (A)

RMS coordinate deviation

(A)

Δτ = 0.1 fs

ε = ± 10

−4

−6

−8

−6

−8

ε = ±

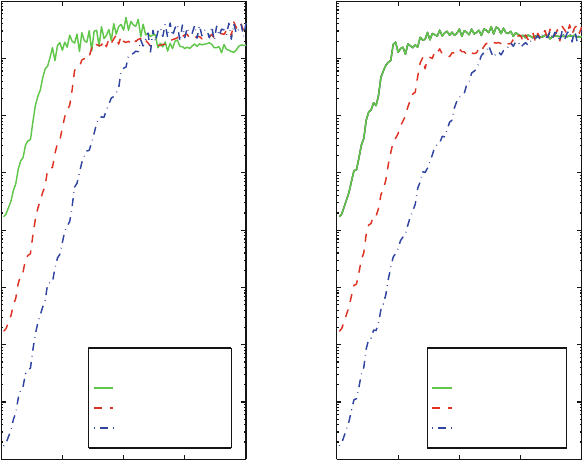
Figure 13.3. The rapid divergence of dynamic trajectories for four water molecules

differing slightly in initial conditions.

This stabilization behavior realized in practice for MD simulations can also

be understood by the different mathematical limit involved in the strict notion of

chaos compared to that relevant for MD. Physicists deﬁne chaos rigorously for

ﬁnite times but in the limit of timesteps approaching zero; in MD applications, we

instead work with ﬁnite timesteps and simulation times approaching inﬁnity.

Statistical View

For many other reasons than inherent chaos, including the approximate nature

of biomolecular simulations, MD trajectories are not intended to animate the

life of a biomolecule faithfully, as if by an unbiased video camera. Rather, our

experimental-by-nature computer ‘snapshots’ aim at gaining structural insights,

which can be tested, and predicting meaningful statistical properties of a complex

system in the ultimate goal of relating structure to function. The more reliable

quantities from MD simulations are thus space and time averaged. This is un-

like differential-equation applications in astrophysics, where precise trajectory

pathways are sought (e.g., planetary orbits). Often, more useful data are obtained

by averaging over, or calculating from, several trajectories rather than from one

long trajectory (e.g., [158, 286, 360, 364, 1428]). This has become very suitable

442 13. Molecular Dynamics: Basics

now with readily available parallel processor architectures and loosely connected

computer networks used for a common goal, as in the folding@home dis-

tributed computing initiative for simulating protein folding and related processes.

Launched in 2001, folding@home has become an international enterprise, with

clients like Sony PlayStations and numerous platforms. See also Skeel’s recent

analysis [1197] for a perturbation analysis on the effect of errors that aims to

show why molecular dynamics simulations “work”.

Let us consider the convergence of the end-to-end distance of a butane mol-

ecule, as ﬁrst illustrated in [304]. Figure 13.4 shows the time evolution of the

end-to-end-distance of the butane molecule for different choices of timesteps in

the range of 0.02 to 2.0 fs. Clearly, different paths are realized even for this very

small system. The associated average end-to-end distance values as a function of

the timestep are the points corresponding to the dashed curve in Figure 13.5.

These data reveal convergence only for small timesteps, less than 0.2 fs. This

value is typically much smaller than standard timesteps used in biomolecular sim-

ulations (0.5 fs or greater). Still, larger values can be quite reasonable depending

on the speciﬁc questions being asked from a simulation.

13.3.5 Simulation Protocol

A careful simulation protocol is essential for MD simulations, to ensure not only

the equilibration phases but also proper enforcement of the boundary conditions

0 100 200 300 400 500 600 700 800 900 1000

7.5

8.5

9.5

10.5

11.5

Time (fs)

End−to−end distance (Angstrom)

0.02 fs

0.2 fs

1.0 fs

2.0 fs

Figure 13.4. Time evolution of the end-to-end distance of butane for different timesteps.

13.3. The Basics: An Overview 443

(when, for example, a biomolecule is placed in a box of water molecules), po-

sitioning of solvent and salt molecules, or computation of the nonbonded terms

and associated pairlist arrays. Also important is monitoring the kinetic tempera-

ture and the energy ﬂuctuations, for the detection of systematic drifts or abrupt

changes, both of which may indicate numerical problems.

For example, severe artifacts arise when the nonbonded energy interactions

are truncated abruptly. This is because the associated force terms rise violently

at the truncation boundary. Improved techniques for smoothly handling the non-

bonded terms are necessary [1220], as described in Chapter 10. The alternative

approach described also in that chapter is to forgo cutoffs and compute all the

nonbonded terms by fast summation techniques such as multipole or Ewald

[142, 486]. Fortunately, such schemes approach linear, rather than quadratic,

dependence on system size.

13.3.6 High-Speed Implementations

High-speed computers are essential for performing the computationally-intensive

MD simulations [143, 658]. The dynamics of condensed systems was simulated

much earlier this century, but macromolecular applications only gained momen-

tum in the mid-to-late 1980s with the advent of high-speed computing. There are

many reasons why this lag occurred, and the issue at heart is best captured by the

following statement by Frauenfelder and Wolynes [423]:

Whatever complexity means, most people agree that biological

systems have it.

Indeed, the energy landscape is complex for biomolecules [422, 1386, 1387].

The various contacts — be they hydrogen bonds, disulﬁde bonds, or noncovalent

interactions like stacking and favorable electrostatics — are difﬁcult to predict

apriori. Thus, the multidimensional potential energy surface that governs biomo-

lecular structure has many maxima, minima, and saddle points. The distributions

about each favorable or unfavorable state are highly anisotropic, with the width

depending on the entropy associated with that state.

Biomolecules are also asymmetric in comparison to simple systems, such as

homogeneous liquid clusters, which were successfully simulated much earlier.

Certainly, there are symmetries in many aspects of protein and nucleic acid struc-

ture (e.g., many proteins are dimers, and the “ideal” DNA double helix has an

axis of symmetry), but in realistic environments there are many sequence-speciﬁc

motifs and binding interactions with other biomolecules in the environment that

induce local structural variations in macromolecules. These local trends can

produce profound global effects.

The motion of biomolecules is also more complex than that of small or homo-

geneous systems. The collective motion is a superposition of many fundamental

motions that characterize the dynamics of a biomolecule: bond stretches, an-

gle bends, torsions, and combinations of those “normal modes” (see Chapter 9

444 13. Molecular Dynamics: Basics

−3

−2

−1

9.12

9.13

9.14

9.15

9.16

9.17

9.18

Convergence of Butane

s End−to−End Distance

Δ t (fs)

End−to−end distance (Angstrom)

3−timestep integration

1−timestep integration

−3

−2

−1

9.127

9.128

9.129

9.130

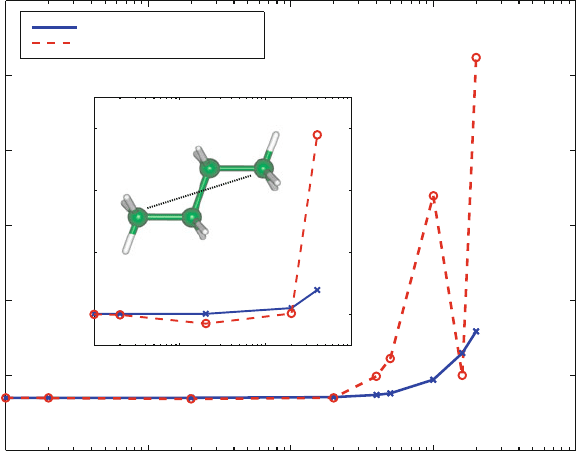
Figure 13.5. Average butane end-to-end distance for single (dashed line) and triple (solid

line) timestep protocols (note logarithmic scale) as computed over 1 ps (see Figure 13.4).

In the latter, the timestep used to deﬁne the data point is the outermost timestep Δt (the

interval of updating the nonbonded forces), with the two smaller values used as Δt/2

and Δt/4 (for updating the dihedral-angle terms and the bond-length and angle terms,

respectively).

for deﬁnitions and examples). Although these components have associated fre-

quencies of disparate magnitudes, the overall motion of a biomolecule is highly

cooperative. That is, small local ﬂuctuations can trigger a chain of events that will

lead to a large global rearrangement. Energy transfer among vibrational modes

may also be involved.

In addition to the overall asymmetry and complexity (of energy landscape

and motion), the solvent and ions in the environment inﬂuence the structure

and dynamics of biomolecules profoundly. Solvent molecules surround and inter-

penetrate proteins and nucleic acids and damp many characteristic motions that

might be present in vacuum. Similarly, ions (sodium, calcium, magnesium, etc.)

inﬂuence structure and dynamics signiﬁcantly, especially of the polyelectrolytic

nucleic acids [850, for example]. Thus, for physical reliability, these long-range

electrostatic interactions are essential to consider in MD simulations of macro-

molecules. This has proven especially important for stabilizing DNA simulations

and accurately describing kinetic processes involving conformational transitions

of DNA [219,220].

13.3. The Basics: An Overview 445

13.3.7 Analysis and Visualization

Careful analysis of the results and visualization techniques are also essential

components of biomolecular simulations today. With the increasing ease and ac-

cessibility of generating computer trajectories, the challenge remains of carefully

analyzing the voluminous data to distill the essential ﬁndings. While many scalar

and vector functions can be computed from a long series of conﬁgurations, under-

standing the dynamics behavior requires a combination of sophisticated analysis

and chemical/biological intuition.

Molecular graphics techniques were more of a problem in the early days of

molecular mechanics than they are now. Before the surge of graphics innovations,

researchers relied more heavily on mechanical models and physical sense (see

related comment in this book’s Preface).

These days, molecular modeling software and analysis tools have become a

large industry. Many sophisticated and useful tools are available to both ex-

perimentalists and computational/theoretical chemists. The dazzling capability

of computer graphics today to render and animate a large, complex three-

dimensional image — often so “real” in appearance that the source may be

obscured — has certainly made biological interpretation much easier, but one

still has to know exactly where, and for what, to look!

13.3.8 Reliable Numerical Integration

To increase the reliability of macromolecular simulations, special care is needed

to formulate efﬁcient numerical procedures for generating dynamic trajectories.

Mathematically, there are classes of methods for conservative Hamiltonian sys-

tems termed symplectic that possess favorable numerical properties in theory and

practice [1090]. In particular, these schemes preserve volumes in phase space (as

measured rigorously by the Jacobian of the transformation from one set of coordi-

nates and momenta to the next). This preservation in turn implies certain physical

invariants for the system.

Another view of symplectic integration is that the computed trajectory (with

associated Hamiltonian H(X

)) remains close in time to the solution of a

nearby Hamiltonian



H. This proximity is rigorously deﬁned as a trajectory whose

energy is order O(Δt)

away from the initial value of the true Hamiltonian H:

H ≡

)

M(V

)+E(X

) ,

where p is the order of the integrator, and X

and V

are the collective position

and velocity vectors at time nΔt. This symplectic property translates to good

long-time behavior in practice: small ﬂuctuations about the initial (conserved in

theory) value of H, and no systematic drift in energy, as might be realized by a

nonsymplectic method.

Figure 13.6 illustrates this favorable symplectic behavior for a simple nonlinear

system, a cluster of four water molecules, integrated by Verlet and by the classical

446 13. Molecular Dynamics: Basics

0 2 4 6 8 10 12 14 16 18 20

−27.5

−27

−26.5

−26

−25.5

−25

Velocity Verlet, Δ

= 1 fs

Runge−Kutta 4, Δ

= 1 fs

0 2 4 6 8 10 12 14 16 18 20

−25.464

−25.4635

−25.463

−25.4625

−25.462

Velocity Verlet, Δ

= 0.1 fs

Runge−Kutta 4, Δ

= 0.1 fs

Time (ps)

Total Energy (Kcal/mol)

Figure 13.6. Energy evolution of a water tetramer simulated by the symplectic Verlet

scheme (solid line) versus the nonsymplectic Runge-Kutta integrator (dashed line) at two

timesteps Δt (0.1 and 1 fs). Note the different energy scales of the plots.

fourth-order (nonsymplectic) Runge-Kutta method. A clear damping trend (i.e.,

decrease of energy with time) is seen by the latter, non-symplectic integrator,

especially at the larger timestep (top).

While symplectic methods can follow kinetics accurately (assuming the

force ﬁeld is adequate), other approaches as discussed in the next chapter —

Langevin and Brownian dynamics — can be effective for thermodynamic sam-

pling. Though additional terms are added (e.g., random thermal forces), enhanced

sampling made possible by larger timesteps can yield more information on the

thermally-accessible conﬁguration space.

13.3.9 Computational Complexity

Intensive Requirements

Trimming the computational time of MD simulations remains a challenge [1110].

As seen from Table 1.2 of Chapter 1, the all-atom molecular models used for

biomolecules are quite large (thousands of atoms). The energy and derivative

computations required at each dynamic step are expensive and limit the total

time that can be simulated: typical timesteps (1 fs) imply one million integration

steps per nanosecond. Interestingly, Table 1.2 also shows our tendency to increase

13.3. The Basics: An Overview 447

system size rather than the simulation time. This can be explained, in part, by the

desire to model more complex and realistic systems and by the timespan/sampling

limitation of MD. Dynamic motions over substantially longer times, as well as

larger spatial scales, can only be approximated through macroscopic models of

proteins and DNA (see [1119] for example).

To reduce computational time of MD simulations, two basic routes can be taken

and combined: reducing the work per timestep, and/or increasing the integration

timestep, Δt. In the latter case, the parameter we aim to lengthen is that associated

with long-range force calculations, that is, the ‘outermost timestep’ in multiple-

timestep (MTS) methods.

Less Work Per Step

Reducing the work per step can be achieved with various protocols used in

practice: employing cutoff ranges for the nonbonded interactions, updating the

nonbonded pairlist infrequently (i.e., less often than every outer timestep), and

reducing the number of degrees of freedom by constraining certain molecular

regions (e.g., protein residues revealed by experiment not to be important for a

certain localized transition).

Larger Timesteps: Accuracy vs. Stability

The maximum value for the outer timestep that can be successfully used is limited

by both accuracy and stability considerations, as will be detailed below. Essen-

tially, instability of a trajectory is easily detected when coordinates and energies

grow uncontrollably. This often signals that the timestep is too large. However,

unless the timestep is far too large, this instability may only be apparent from a

trajectory of length of hundreds of picoseconds or longer. The guidelines for sta-

bility for a given integrator are often derived from linear analysis (i.e., theoretical

analysis for a harmonic oscillator) [866,967, 1437, for example]. In practice, the

timestep must typically be smaller than this limit for complex nonlinear problems

to ensure stability as well as reasonable accuracy.

Accuracy limits the timestep Δt in the sense that the resolution produced

must be adequate for the processes being followed and the measurements tar-

geted. Thus, a simulation may be stable but the timestep too large to capture

high-frequency ﬂuctuations accurately.

Closely related to stability and accuracy are resonance artifacts. This topic of

recent interest will be discussed separately.

Techniques for increasing the timestep range from constraining the fastest

degrees of freedom via algebraic constraints to using multiple-timestep (MTS)

schemes to formulating rigid-body dynamics. For recent reviews, see [1110,

1118], for example.

Constraining Fastest Motions

The technique of constrained dynamics has been used for a long time to enforce

rigidity of bond lengths [868,1079,1291,1292]. This approach helps increase the

448 13. Molecular Dynamics: Basics

timestep by a typical factor of two (e.g., from 1 to 2 fs), with similar gains in

the computational time. Freezing bond angles, however, alters the overall motion

substantially [1296]. See the last section of this chapter.

Splitting Forces in MTS Schemes

In MTS schemes, we divide the force components into classes and update the

associated forces at timesteps appropriate for the class. Three-class partitioning

schemes are common in biomolecular simulations, though more classes can be

used for added accuracy/efﬁciency.

For example, a simple partitioning based on potential-energy components

[1349] can place bond-length and bond-angleterms into the fastest class, dihedral-

angle terms into the medium class, and the remaining forces into the slow-force

class. Incorporating distance classes (e.g., interactions within 6

A into the

medium-force class) involves more complex bookkeeping work for the non-

bonded pairlist generation but often works better. The numerical details of how

these different updates are merged affect the stability of the trajectory signiﬁcantly

[94,134]; see the separate section on MTS methods in the next chapter for details.

To illustrate a simple MTS scheme, consider using three timesteps for the bu-

tane system analyzed above for computing the end-to-end distance. We set the

three values as Δτ,2Δτ ,and4Δτ ≡ Δt; thus a 3-timestep integrator associated

with the outer timestep of Δt =2fs has an inner timestep of 0.5 fs and a medium

timestep of 1 fs. Bond-length and angle terms are updated every Δτ; dihedral-

angle terms are updated every 2Δτ; and nonbonded interactions are recalculated

every 4Δτ for this butane model. This partitioning should thus save work for this

MTS protocol {Δτ,2Δτ, 4Δτ} relative to the single-timestep integrator at Δτ.

The data shown in Figure 13.5 for the average end-to-end distance of bu-

tane compares values obtained from single-timestep methods to those obtained

by Verlet-based MTS simulations. We see that the accuracy is determined

by the innermost timestep. This is precisely the advantage exploited in MTS

schemes: same accuracy at less computation (under the appropriate comparison)

[579,1448].

For the small butane system, the MTS force splitting is not computation-

ally advantageous because the nonbonded interactions represent a small fraction

of the total force-evaluation work. However, for biomolecules, non-negligible

speedups (e.g., factor of 2 or more) can be reaped with respect to single-timestep

simulations performed at the inner timestep (Δτ) used in the MTS protocol.

13.4 The Verlet Algorithm

One of the simplest and best family of integrators for biomolecular dynamics is

the leapfrog/ Verlet/ St¨ormer group. The basic scheme was derived as a truncation

of a higher-order method used by St¨ormer in 1907 [1227] to integrate trajectories

of electrons. The scheme was adapted by Verlet 60 years later [1302]. A favorable

13.4. The Verlet Algorithm 449

numerical property of this family is exceptional stability over long times (recall

the example in Figure 13.6, where the Verlet trajectory shows favorable energy

conservation compared to the Runge-Kutta trajectory).

Stability far more than accuracy limits the timestep in simulations of biomo-

lecular motion governed by approximate force ﬁelds. Programming ease is a

boon for weary simulators who must wade through thousands of lines of molec-

ular mechanics and dynamics programs. Far from mere convenience, simplicity

in the integration also facilitates the implementation of variations in the basic

method (e.g., constrained dynamics, extensions to various statistical ensembles)

and the merging of integration schemes with other program components (e.g., fast

electrostatics by the particle-mesh Ewald method).

For both these practical and theoretical reasons, it has become very difﬁcult

for alternative schemes — such as higher-order and implicit discretizations —

to compete with Verlet in popularity [1110]. For the same reason, the single-

timestep Verlet method is still more popular in general than MTS variants (as

introduced in Subsection 13.3.9 and discussed in detail in the next chapter), but

this is likely to change as comprehensive and reliable MTS routines for various

statistical ensembles enter into the popular biomolecular dynamics packages.

Not surprisingly, generalizations of the Verlet method have been applied to

other formulations, such as constrained and stochastic dynamics. The Verlet

scheme is also the basis of the common force-splitting MTS methods and for

approaches using various thermodynamic ensembles.

Below we describe how the scheme is formulated and derive its leapfrog,

velocity, and position variants.

13.4.1 Position and Velocity Propagation

Iterative Recipe

To derive the Verlet propagation scheme for Newtonian dynamics, we write the

equation of motion, eq. (13.3), as

X(t)=F (X(t)) (13.7)

where

F (X(t)) = −∇E(X(t)) . (13.8)

We also use the symbol



F (the acceleration, or the force scaled by the inverse-

mass matrix) to simplify the formulas below, where



F (X(t)) = M

−1

F (X(t)) = −M

−1

∇E(X(t)) . (13.9)

In a numerical discretization, a timestep Δt is chosen and the continuous variables

X(t) and V (t) are approximated by values at discrete time intervals nΔt for

n =0, 1, 2,... ,denoted as X

and V

. Below we also use the notation F

short hand for the force at time nΔt, namely F(X

). Similarly,



represents

the numerical estimate to the acceleration at time nΔt:



F (X

450 13. Molecular Dynamics: Basics

An iterative formula is then chosen to deﬁne recursively the positions and

velocities of the molecular system. If the formula deﬁnes the solution at timestep

n +1in terms of quantities determined at previous iterates, as in

n+1

= V

+Δt



the discretization method is explicit. If instead the new solution is deﬁned

implicitly, in terms of known and unknown quantities, as in

n+1

= V

+Δt



n+1

the method is implicit. The explicit versions generally involve simple algorithms

that (for propagation only) use modest memory, while implicit methods involve

more complex algorithms but may enjoy enhanced stability properties.

Position Update

The original Verlet algorithm [1302] describes an update for trajectory positions,

as follows:

n+1

=2X

− X

n−1

+Δt



. (13.10)

This is a two-step propagation scheme since positions from two prior steps (n and

n−1) must be stored. A one-step scheme — preferable in terms of storage — can

be obtained by using V

instead of X

n−1

as a variable on the left-hand side (see

below).

The Verlet algorithm is fourth-order accurate in position. To see this, use the

Taylor expansion around X(t) to obtain:

X(t +Δt)+X(t − Δt)

= X(t)+ΔtV(t)+

Δt



F (X(t)) +

Δt

V (t)+O(Δt

)

+ X(t) − ΔtV(t)+

Δt



F (X(t)) −

Δt

V (t)+O(Δt

)

=2X(t)+Δt



F (X(t)) + O(Δt

) . (13.11)

Velocity Update

The ﬂexibility in deﬁning compatible velocity formulas from the Verlet position

propagation formula (eq. (13.10)) has led to Verlet variants. These variants rely

on a velocity formula consistent with eq. (13.10).

We derive such a formula by subtracting the Taylor expansion for X(t − Δt)

from that for X(t +Δt), instead of adding as done above, to obtain:

X(t +Δt) −X(t − Δt)

2Δt

= V (t)+O(Δt

) . (13.12)

This deﬁnition can be written as the central difference approximation

=(X

n+1

− X

n−1

)/(2Δt) . (13.13)