Schutz B. A first course in general relativity

Подождите немного. Документ загружается.

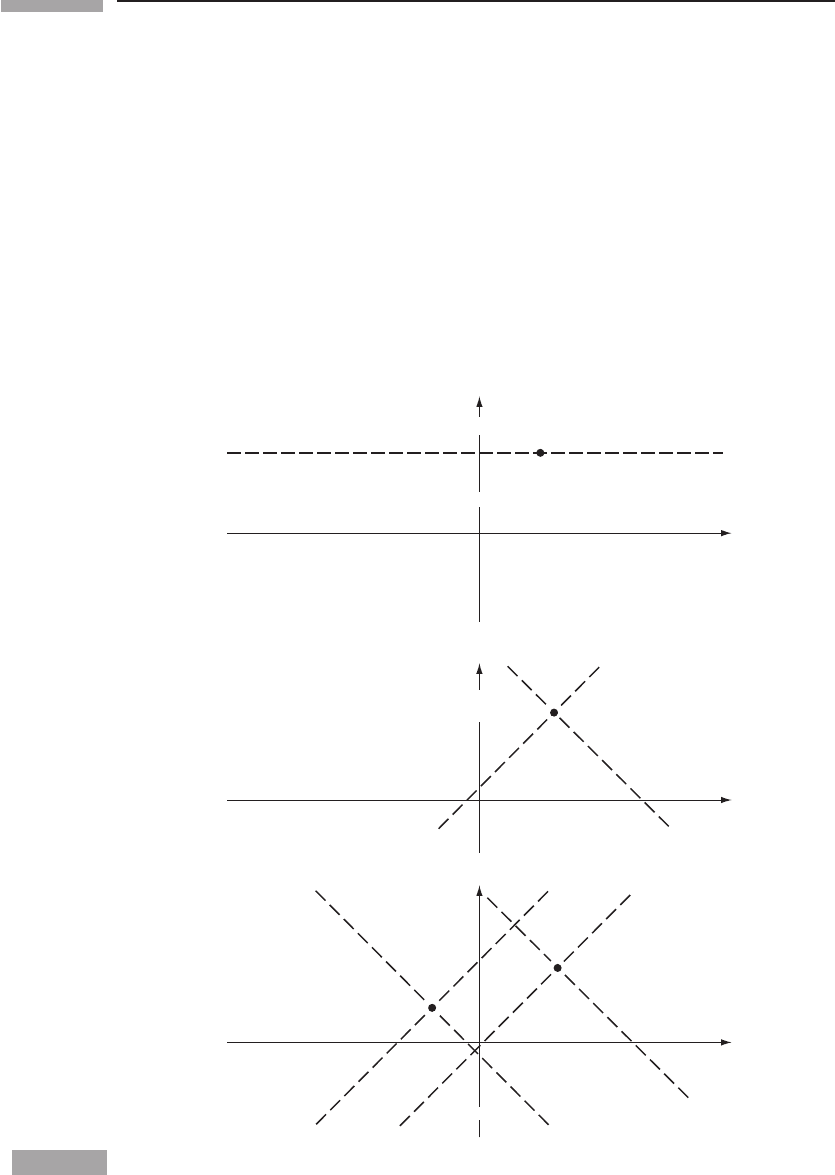
13 1.6 Invariance of the interval

The events that are lightlike separated from any particular event A, lie on a cone whose

apex is A. This cone is illustrated in Fig. 1.8. This is called the light cone of A. All events

within the light cone are timelike separated from A; all events outside it are spacelike

separated. Therefore, all events inside the cone can be reached from A on a world line

which everywhere moves in a timelike direction. Since we will see later that nothing

can move faster than light, all world lines of physical objects move in a timelike direc-

tion. Therefore, events inside the light cone are reachable from A by a physical object,

whereas those outside are not. For this reason, the events inside the ‘future’ or ‘forward’

light cone are sometimes called the absolute future of the apex; those within the ‘past’ or

‘backward’ light cone are called the absolute past; and those outside are called the abso-

lute elsewhere. The events on the cone are therefore the boundary of the absolute past

Galileo:

Einstein:

Two events:

Future of event 

Past of event 

Past of 

‘Elsewhere’

of 

‘Elsewhere’

of 

Future

of 

Common

future

Future

of 

Future

of 

Past of 

Past of 

‘Now’ for

event 

‘Now’ is only

 itself







Common past

Figure 1.9

Old and new concepts of spacetime

14 Special relativity

and future. Thus, although ‘time’ and ‘space’ can in some sense be transformed into one

another in SR, it is important to realize that we can still talk about ‘future’ and ‘past’ in

an invariant manner. To Galileo and Newton the past was everything ‘earlier’ than now;

all of spacetime was the union of the past and the future, whose boundary was ‘now’. In

SR, the past is only everything inside the past light cone, and spacetime has three invari-

ant divisions: SR adds the notion of ‘elsewhere’. What is more, although all observers

agree on what constitutes the past, future, and elsewhere of a given event (because the

interval is invariant), each different event has a different past and future; no two events

have identical pasts and futures, even though they can overlap. These ideas are illustrated

in Fig. 1.9.

1.7 Invariant hyperbolae

We can now calibrate the axes of

O’s coordinates in the spacetime diagram of O,Fig.1.5.

We restrict ourselves to the t −x plane. Consider a curve with the equation

−t

+ x

= a

where a is a real constant. This is a hyperbola in the spacetime diagram of O, and it

passes through all events whose interval from the origin is a

. By the invariance of the

interval, these same events have interval a

from the origin in

O, so they also lie on the

curve −

+¯x

= a

. This is a hyperbola spacelike separated from the origin. Similarly,

the events on the curve

−t

+ x

=−b

all have timelike interval −b

from the origin, and also lie on the curve −

+¯x

=−b

These hyperbolae are drawn in Fig. 1.10. They are all asymptotic to the lines with slope

±1, which are of course the light paths through the origin. In a three-dimensional diagram

(in which we add the y axis, as in Fig. 1.8), hyperbolae of revolution would be asymptotic

to the light cone.

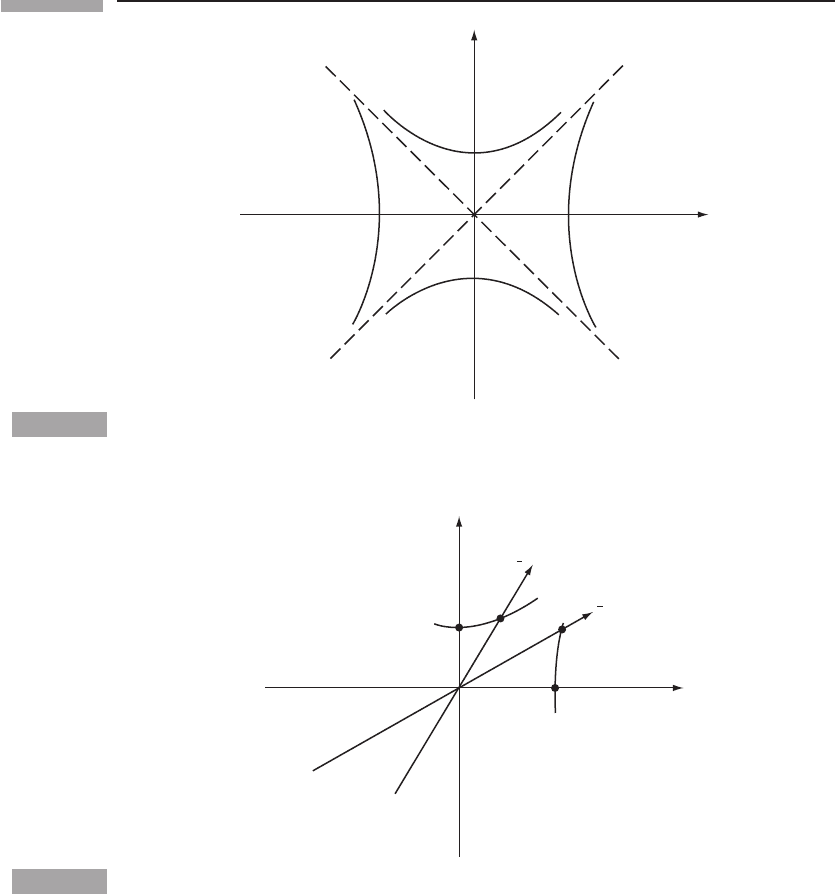
We can now calibrate the axes of

O.InFig.1.11 the axes of O and

O are drawn, along

with an invariant hyperbola of timelike interval −1 from the origin. Event A is on the t

axis, so has x = 0. Since the hyperbola has the equation

−t

+ x

=−1,

it follows that event A has t = 1. Similarly, event B lies on the

t axis, so has ¯x = 0. Since

the hyperbola also has the equation

−

+¯x

=−1,

it follows that event B has

t = 1. We have, therefore, used the hyperbolae to calibrate the

axis. In the same way, the invariant hyperbola

−t

+ x

= 4

15 1.7 Invariant hyperbolae

–a

–b

Figure 1.10

Invariant hyperbolae, for a > b.









Figure 1.11

Using the hyperbolae through events

A and E to calibrate the

x and

t axes.

shows that event E has coordinates t = 0, x = 2 and that event F has coordinates

t = 0,

¯x = 2. This kind of hyperbola calibrates the spatial axes of

Notice that event B looks to be ‘further’ from the origin than A.Thisagainshows

the inappropriateness of using geometrical intuition based upon Euclidean geometry. Here

the important physical quantity is the interval −(t)

+ (x)

, not the Euclidean distance

(t)

+ (x)

. The student of relativity has to learn to use s

as the physical measure of

‘distance’ in spacetime, and he has to adapt his intuition accordingly. This is not, of course,

in conﬂict with everyday experience. Everyday experience asserts that ‘space’ (e.g. the

16 Special relativity

section of spacetime with t = 0) is Euclidean. For events that have t = 0 (simultaneous

to observer O), the interval is

s

= (x)

+ (y)

+ (z)

This is just their Euclidean distance. The new feature of SR is that time can (and must)

be brought into the computation of distance. It is not possible to deﬁne ‘space’ uniquely

since different observers identify different sets of events to be simultaneous (Fig. 1.5). But

there is still a distinction between space and time, since temporal increments enter s

with the opposite sign from spatial ones.





(b)

(a)





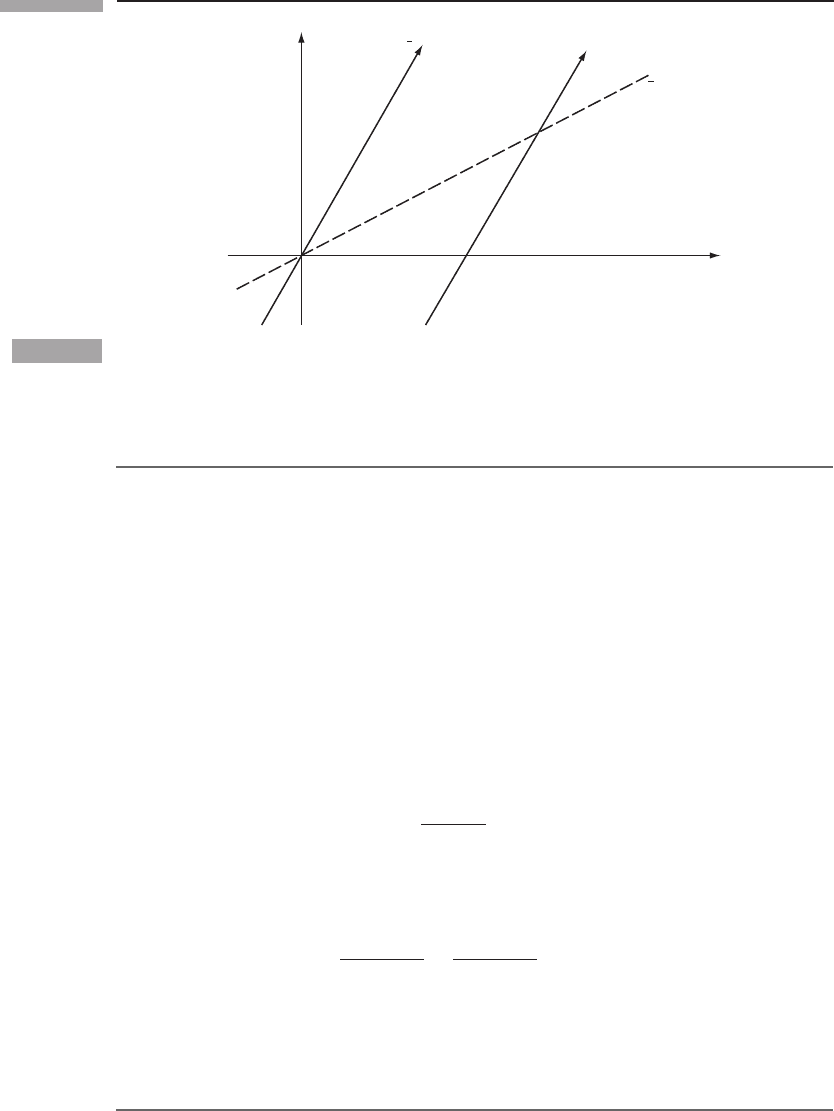
Figure 1.12

(a) A line of simultaneity in

O is tangent to the hyperbola at P. (b) The same tangency as seen

17 1.8 Particularly important results

In order to use the hyperbolae to derive the effects of time dilation and Lorentz contrac-

tion, as we do in the next section, we must point out a simple but important property of the

tangent to the hyperbolae.

In Fig. 1.12(a) we have drawn a hyperbola and its tangent at x = 0, which is obviously

a line of simultaneity t = const. In Fig. 1.12(b) we have drawn the same curves from the

point of view of observer

O who moves to the left relative to O. The event P has been

shifted to the right: it could be shifted anywhere on the hyperbola by choosing the Lorentz

transformation properly. The lesson of Fig. 1.12(b) is that the tangent to a hyperbola at any

event P is a line of simultaneity of the Lorentz frame whose time axis joins P to the origin.

If this frame has velocity v, the tangent has slope v.

1.8 Particularly important results

Time dilation

From Fig. 1.11 and the calculation following it, we deduce that when a clock moving on the

t axis reaches B it has a reading of

t = 1, but that event B has coordinate t = 1/

√

(1 − v

)

in O.SotoO it appears to run slowly:

(t)

measured in O

(

t )

measured in

√

(1 − v

)

. (1.8)

Notice that 

t is the time actually measured by a single clock, which moves on a world

line from the origin to B, while t is the difference in the readings of two clocks at rest

in O; one on a world line through the origin and one on a world line through B . We shall

return to this observation later. For now, we deﬁne the proper time between events B and

the origin to be the time ticked off by a clock which actually passes through both events. It

is a directly measurable quantity, and it is closely related to the interval. Let the clock be

at rest in frame

O, so that the proper time τ is the same as the coordinate time 

t. Then,

since the clock is at rest in

O,wehave¯x = ¯y = ¯z = 0, so

s

=−

=−τ

. (1.9)

The proper time is just the square root of the negative of the interval. By expressing the

interval in terms of O’s coordinates we get

τ = [(t)

− (x)

− (y)

− (z)

]

1/2

= t

√

(1 − v

). (1.10)

This is the time dilation all over again.

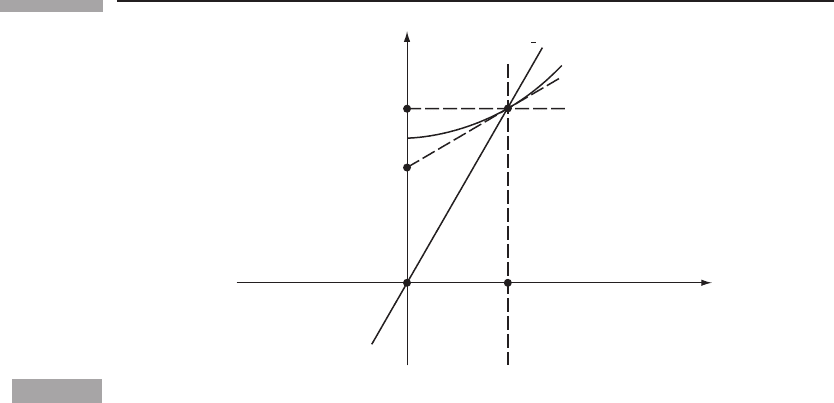
18 Special relativity







Rear of rod

Front of rod

Figure 1.13

The proper length of

AC is the length of the rod in its rest frame, while that of AB is its length

Lorentz contraction

In Fig. 1.13 we show the world path of a rod at rest in

O. Its length in

O is the square

root of s

, while its length in O is the square root of s

. If event C has coordinates

t = 0, ¯x = l, then by the identical calculation from before it has x coordinate in O

= l/

√

(1 − v

and since the ¯x axis is the line t = vx,wehave

= vl/

√

(1 − v

The line BC has slope (relative to the t-axis)

x/t = v,

and so we have

− x

− t

= v,

and we want to know x

when t

= 0. Thus,

= x

− vt

√

(1 − v

)

−

√

(1 − v

)

= l

√

(1 − v

). (1.11)

This is the Lorentz contraction.

Conventions

The interval s

is one of the most important mathematical concepts of SR but there

is no universal agreement on its deﬁnition: many authors deﬁne s

= (t)

− (x)

−

19 1.8 Particularly important results

(y)

− (z)

. This overall sign is a matter of convention (like the use of Latin and Greek

indices we referred to earlier), since invariance of s

implies invariance of −s

.The

physical result of importance is just this invariance, which arises from the difference in

sign between the (t)

and [(x)

+ (y)

+ (z)

] parts. As with other conventions,

students should ensure they know which sign is being used: it affects all sorts of formulae,

for example Eq. (1.9).

Failure of relativity?

Newcomers to SR, and others who don’t understand it well enough, often worry at this

point that the theory is inconsistent. We began by assuming the principle of relativity, which

asserts that all observers are equivalent. Now we have shown that if

O moves relative to O,

the clocks of

O will be measured by O to be running more slowly than those of O.Soisn’t

it therefore the case that

O will measure O ’s clocks to be running faster than his own? If

so, this violates the principle of relativity, since we could as easily have begun with

O and

deduced that O’s clocks run more slowly than

O’s.

This is what is known as a ‘paradox’, but like all ‘paradoxes’ in SR, this comes from

not having reasoned correctly. We will now demonstrate, using spacetime diagrams, that

O measures O’s clocks to be running more slowly. Clearly, we could simply draw the

spacetime diagram from

O’s point of view, and the result would follow. But it is more

instructive to stay in O’s spacetime diagram.

Different observers will agree on the outcome of certain kinds of experiments. For exam-

ple, if A ﬂips a coin, every observer will agree on the result. Similarly, if two clocks are

right next to each other, all observers will agree which is reading an earlier time than the

other. But the question of the rate at which clocks run can only be settled by comparing

the same two clocks on two different occasions, and if the clocks are moving relative to

one another, then they can be next to each other on only one of these occasions. On the

other occasion they must be compared over some distance, and different observers may

draw different conclusions. The reason for this is that they actually perform different and

inequivalent experiments. In the following analysis, we will see that each observer uses two

of his own clocks and one of the other’s. This asymmetry in the ‘design’ of the experiment

gives the asymmetric result.

Let us analyze O’s measurement ﬁrst, in Fig. 1.14. This consists of comparing the read-

ing on a single clock of

O (which travels from A to B) with two clocks of his own: the

ﬁrst is the clock at the origin, which reads

O’s clock at event A; and the second is the

clock which is at F at t = 0 and coincides with

O’s clock at B. This second clock of O

moves parallel to the ﬁrst one, on the vertical dashed line. What O says is that both clocks

at A read t = 0, while at B the clock of

O reads

t = 1,

while that of O reads a later time,

t = (1 −v

)

−1/2

. Clearly,

O agrees with this, as he is just as capable of looking at clock

dials as O is. But for O to claim that

O’s clock is running slowly, he must be sure that

his own two clocks are synchronized, for otherwise there is no particular signiﬁcance in

observing that at B the clock of

O lags behind that of O.Now,fromO’s point of view, his

20 Special relativity











Figure 1.14

The proper length of

AB is the time ticked by a clock at rest in

O,whilethatofAC is the time it

takestodosoasmeasuredby

clocks are synchronized, and the measurement and its conclusion are valid. Indeed, they

are the only conclusions he can properly make.

But

O need not accept them, because to him O’s clocks are not synchronized. The dotted

line through B is the locus of events that

O regards as simultaneous to B. Event E is on this

line, and is the tick of O’s ﬁrst clock, which

O measures to be simultaneous with event B.

A simple calculation shows this to be at t = (1 − v

)

1/2

, earlier than O’s other clock at B,

which is reading (1 − v

)

−1/2

.So

O can reject O’s measurement since the clocks involved

aren’t synchronized. Moreover, if

O studies O’s ﬁrst clock, he concludes that it ticks from

t = 0tot = (1 −v

)

1/2

(i.e. from A to B) in the time it takes his own clock to tick from

t = 0to

t = 1 (i.e. from A to B). So he regards O’s clocks as running more slowly than

his own.

It follows that the principle of relativity is not contradicted: each observer measures the

other’s clock to be running slowly. The reason they seem to disagree is that they measure

different things. Observer O compares the interval from A to B with that from A to C.The

other observer compares that from A to B with that from A to E. All observers agree on

the values of the intervals involved. What they disagree on is which pair to use in order to

decide on the rate at which a clock is running. This disagreement arises directly from the

fact that the observers do not agree on which events are simultaneous. And, to reiterate a

point that needs to be understood, simultaneity (clock synchronization) is at the heart of

clock comparisons: O uses two of his clocks to ‘time’ the rate of

O’s one clock, whereas

O uses two of his own clocks to time one clock of O.

Is this disagreement worrisome? It should not be, but it should make the student very

cautious. The fact that different observers disagree on clock rates or simultaneity just means

that such concepts are not invariant: they are coordinate dependent. It does not prevent any

given observer from using such concepts consistently himself. For example, O can say that

A and F are simultaneous, and he is correct in the sense that they have the same value of the

coordinate t. For him this is a useful thing to know, as it helps locate the events in spacetime.

21 1.9 The Lorentz transformation

Any single observer can make consistent observations using concepts that are valid for

him but that may not transfer to other observers. All the so-called paradoxes of relativity

involve, not the inconsistency of a single observer’s deductions, but the inconsistency of

assuming that certain concepts are independent of the observer when they are in fact very

observer dependent.

Two more points should be made before we turn to the calculation of the Lorentz trans-

formation. The ﬁrst is that we have not had to deﬁne a ‘clock’, so our statements apply

to any good timepiece: atomic clocks, wrist watches, circadian rhythm, or the half-life of

the decay of an elementary particle. Truly, all time is ‘slowed’ by these effects. Put more

properly, since time dilation is a consequence of the failure of simultaneity, it has nothing

to do with the physical construction of the clock and it is certainly not noticeable to an

observer who looks only at his own clocks. Observer

O sees all his clocks running at the

same rate as each other and as his psychological awareness of time, so all these processes

run more slowly as measured by O . This leads to the twin ‘paradox’, which we discuss

later.

The second point is that these effects are not optical illusions, since our observers exer-

cise as much care as possible in performing their experiments. Beginning students often

convince themselves that the problem arises in the ﬁnite transmission speed of signals, but

this is incorrect. Observers deﬁne ‘now’ as described in § 1.5 for observer

O, and this is

the most reasonable way to do it. The problem is that two different observers each deﬁne

‘now’ in the most reasonable way, but they don’t agree. This is an inescapable consequence

of the universality of the speed of light.

1.9 The Lorentz transformation

We shall now make our reasoning less dependent on geometrical logic by studying the

algebra of SR: the Lorentz transformation, which expresses the coordinates of

O in terms

of those of O. Without losing generality, we orient our axes so that

O moves with speed

v on the positive x axis relative to O. We know that lengths perpendicular to the x axis

are the same when measured by O or

O. The most general linear transformation we need

consider, then, is

t = αt +βx ¯y = y,

¯x = γ t + σ x ¯z = z,

where α, β, γ , and σ depend only on v.

From our construction in § 1.5 (Fig. 1.4) it is clear that the

t and ¯x axes have the

equations:

t axis (¯x = 0) : vt − x = 0,

¯x axis (

t = 0) : vx − t = 0.

The equations of the axes imply, respectively:

γ/

σ =−v, β/α =−v,

22 Special relativity

which gives the transformation

t = α(t −vx),

¯x = σ (x −vt).

Fig. 1.4 gives us one other bit of information: events (

t = 0, ¯x = a) and (

t = a, ¯x = 0) are

connected by a light ray. This can easily be shown to imply that α = σ . Therefore we have,

just from the geometry:

t = α(t −vx),

¯x = α(x − vt).

Now we use the invariance of the interval:

−(

+ (¯x)

=−(t)

+ (x)

This gives, after some straightforward algebra,

α =±1/

√

(1 − v

We must select the + sign so that when v = 0 we get an identity rather than an inversion

of the coordinates. The complete Lorentz transformation is, therefore,

t =

√

(1 − v

)

−

√

(1 − v

)

¯x =

−vt

√

(1 − v

)

√

(1 − v

)

¯y = y,

¯z = z.

(1.12)

This is called a boost of velocity v in the x direction.

This gives the simplest form of the relation between the coordinates of

O and O. For this

form to apply, the spatial coordinates must be oriented in a particular way:

O must move

with speed v in the positive x direction as seen by O, and the axes of

O must be parallel to

the corresponding ones in O. Spatial rotations of the axes relative to one another produce

more complicated sets of equations than Eq. (1.12), but we will be able to get away with

Eq. (1.12).

1.10 T h e ve l oc i ty - co m po s it i on l aw

The Lorentz transformation contains all the information we need to derive the standard

formulae, such as those for time dilation and Lorentz contraction. As an example of its use

we will generalize the Galilean law of addition of velocities (§ 1.1).