Шапкин А.С., Шапкин В.А. Задачи по высшей математике, теории вероятностей, математической статистике, математическому программированию с решениями
Подождите немного. Документ загружается.


411
2. Íàéòè îáùåå ðåøåíèå ñèñòåìû â âèäå
x
1
= f (x
3
, x
4
, x
5
),
x
2
= ϕ (x
3
, x
4
, x
5
).
3. Íàéòè ÷àñòíîå ðåøåíèå ñèñòåìû
),(
54321
, , , ,
xxxxxa =
ïî-
ëîæèâ õ
3
= m, õ
4
= n, õ
5
= m n è ïðîâåðèòü ñèñòåìó.
1.5. Ñîáñòâåííûå ÷èñëà è ñîáñòâåíûå âåêòîðû
1.5.1. Íàéòè ñîáñòâåííûå ÷èñëà è ñîîòâåòñòâóþùèå èì ñîá-
ñòâåííûå âåêòîðû äëÿ ìàòðèöû
.
0
−
=
m
nnm
A
2. Àíàëèòè÷åñêàÿ ãåîìåòðèÿ
2.1. Ïðÿìàÿ íà ïëîñêîñòè
2.1.1. Íà ïðÿìóþ mx + ny m
2
n
2
= 0, ñïîñîáíóþ îòðàæàòü
ëó÷è, ïàäàåò ëó÷ 2nx + my 3mn = 0. Ñîñòàâèòü óðàâíåíèå îòðà-
æåííîãî ëó÷à.
2.1.2. Äàí òðåóãîëüíèê ÀÂÑ ñ âåðøèíàìè À (m + 1; n + 1), B
(m; n) è Ñ (m; n). Íàéòè:
à) âåëè÷èíó óãëà À;
á) êîîðäèíàòû òî÷êè ïåðåñå÷åíèÿ ìåäèàí;
â) êîîðäèíàòû òî÷êè ïåðåñå÷åíèÿ âûñîò;
ã) äëèíó âûñîòû, îïóùåííîé èç âåðøèíû À;
ä) ïëîùàäü òðåóãîëüíèêà ÀÂÑ;
å) ñèñòåìó íåðàâåíñòâ, çàäàþùèõ îáëàñòü âíóòðè òðåóãîëüíè-
êà ÀÂÑ, è ñäåëàòü ÷åðòåæ.
2.2. Êðèâûå âòîðîãî ïîðÿäêà íà ïëîñêîñòè
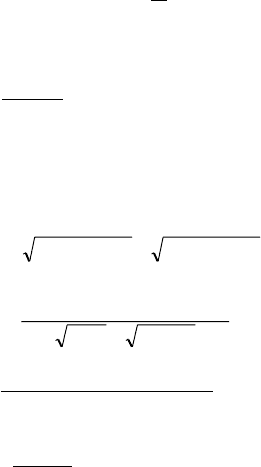
2.2.1. Ñîñòàâèòü óðàâíåíèå êðèâîé, äëÿ êàæäîé òî÷êè êîòî-
ðîé îòíîøåíèå ðàññòîÿíèÿ äî òî÷êè F (n; m) ê ðàññòîÿíèþ äî ïðÿ-
ìîé x = m ðàâíî
.
n
m
Ïðèâåñòè ýòî óðàâíåíèå ó êàíîíè÷åñêîìó
âèäó è îïðåäåëèòü òèï êðèâîé.
412
2.3. Ïðÿìàÿ è ïëîñêîñòü â ïðîñòðàíñòâå
2.3.1. Ïèðàìèäà SABC çàäàíà âåðøèíàìè S (m; n; m + n),
A (m + 1; n; m), B (n; m + 1; n), C (n; m; m n). Íàéòè:
à) óðàâíåíèå ïëîñêîñòè, ïðîõîäÿùåé ÷åðåç òî÷êè À,  è Ñ;
á) âåëè÷èíó óãëà ìåæäó ðåáðîì SC è ãðàíüþ ÀÂÑ;
â) ïëîùàäü ãðàíè ÀÂÑ;
ã) óðàâíåíèå âûñîòû, îïóùåííîé èç âåðøèíû S íà ãðàíü ÀÂÑ
è åå äëèíó;
ä) îáúåì ïèðàìèäû SABC.
3. Äèôôåðåíöèàëüíîå èñ÷èñëåíèå
3.1. Ïîñòðîåíèå ãðàôèêîâ ýëåìåíòàðíûõ ôóíêöèé
3.1.1. Ñ ïîìîùüþ ñìåùåíèÿ, ðàñòÿæåíèÿ è îòðàæåíèÿ ãðàôè-
êîâ ôóíêöèé y = x
2
è
x
y
1
=
ïîñòðîèòü ãðàôèêè ôóíêöèé:
à)
; |2|
222
nmmxxy −+−=
á)
.
nxm
nmx
y
−
+
=
3.2. Ïðåäåëû, íåïðåðûâíîñòü è ðàçðûâû ôóíêöèé
3.2.1. Íàéòè ïðåäåëû ôóíêöèé:
à)
; lim
22
+−−++
±∞→
mnxxnmxx
x
á)
;
2
)(
lim
222
/
nmxmx
mnxnmmnx
mnx
+−
++−
→
â)
;
)( cos1
) )(( cos)( cos
lim
0
nx
xnmmx
x
−
+−
→
ã)
; lim
)(
xnm
x
nmx
nmx
+
∞→
+
−
ä)
.
)(
2
))2((coslim
mx
x
nx
ctg
π
→
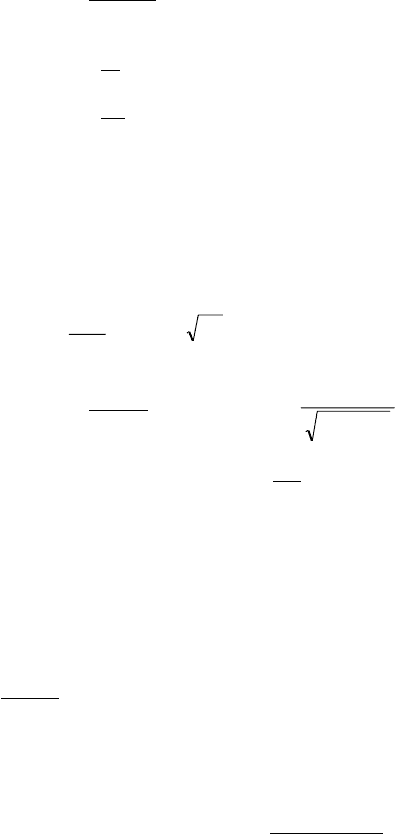
413
3.2.2.  òî÷êàõ õ
1
= 0 è õ
2
= n äëÿ ôóíêöèè f (x) óñòàíîâèòü
íåïðåðûâíîñòü èëè îïðåäåëèòü õàðàêòåð òî÷åê ðàçðûâà. Íàðèñî-
âàòü ãðàôèê ôóíêöèè f (x) â îêðåñòíîñòÿõ ýòèõ òî÷åê:
à)
;
22
)(
/
−
=
xn
m
x
f
á)
+∞<<
≤≤−
<<∞+
=
;åñëè,
,0åñëè,)(
,0åñëè),(
)(
2
2
xnmx
nxnx
n
m
xnx
n
m
xf
3.3. Ïðîèçâîäíûå ôóíêöèé
3.3.1. Íàéòè ïðîèçâîäíûå y ′(x) ôóíêöèé:
à)
;
1
41
1
1
nm
m
n
mnxx
n
y
+
+
+
++⋅
+
=
á)
;
/
)1(
n
xm
ny
+=
â)
;
)/(
ln
nmm
m
nx
nmx
y
+
+
+
=
ã)
;
)(1
)( arcsin
2
nx
nx
y
−
=
ä)
;
)( sin
)(
mx
nx
y
=
e)
;
mn
my
nx
e
nymx
=−
+
æ)
++=
++=
.2
,)( ln
2
mntnty
mntmtx
3.4. Ïðèëîæåíèÿ ïðîèçâîäíîé
3.4.1. Ñîñòàâèòü óðàâíåíèÿ êàñàòåëüíûõ ê ãðàôèêó ôóíêöèè
,
nmx
nmx
y
−
+
=
ïàðàëëåëüíûõ ïðÿìîé 2mx + ny + mn = 0.
3.4.2. Íàéòè íàèáîëüøåå è íàèìåíüøåå çíà÷åíèÿ ôóíêöèè
f (x) = 2õ
3
+ 3 (m n) õ
2
6mnõ + 1 íà îòðåçêå [m n; m + n].
3.4.3. Ñ ïîìîùüþ ìåòîäîâ äèôôåðåíöèàëüíîãî èñ÷èñëåíèÿ
ïîñòðîèòü ãðàôèê ôóíêöèè
.
22
3
)(
)(
nmx
mx
y
−−
−
=
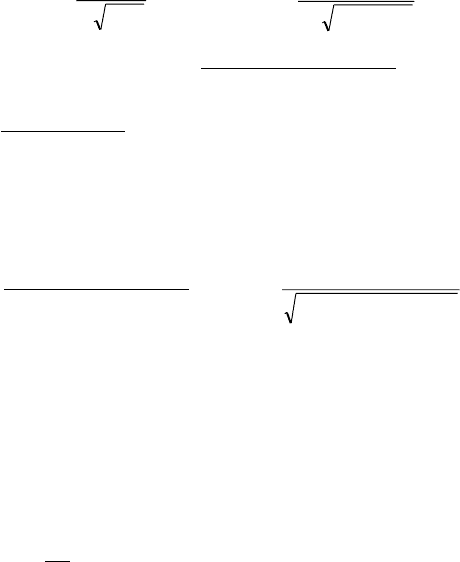
414
3.5. Ïðèáëèæåííîå ðåøåíèå àëãåáðàè÷åñêèõ óðàâíåíèé
3.5.1. Äëÿ óðàâíåíèÿ mõ cos (nõ) = 0 îòäåëèòü ïîëîæèòåëü-
íûé êîðåíü è íàéòè åãî ïðèáëèæåííî ñ òî÷íîñòüþ
ε
= 0,01:
à) ìåòîäîì äåëåíèÿ îòðåçêà ïîïîëàì;
á) ìåòîäîì êàñàòåëüíûõ.
Ïðèìå÷àíèå. Ìîæíî ñ÷èòàòü, ÷òî òî÷íîñòü
ε
äîñòèãíóòà, åñëè
ðàçíîñòü ìåæäó ñîñåäíèìè ïðèáëèæåíèÿìè x
k + 1
è x
k
óäîâëåòâî-
ðÿåò íåðàâåíñòâó | x
k + 1
x
k
| <
ε
.
4. Èíòåãðàëüíîå èñ÷èñëåíèå
4.1. Íåîïðåäåëåííûé èíòåãðàë
4.1.1. Íàéòè èíòåãðàëû:
à)
;
2
1
1
dxmn
x
n
xm
m
n
n
∫
+−⋅
+
+
á)
;
2
∫
−⋅ nxmxx
dx
â)
;
2
)(
dxemx
nx
−
⋅+
∫
ã)
;
)(2
2223
22
dx
xnmnxx
nmnx
∫
++−
++
ä)
∫
++
.
1)( sin
nmx
dx
4.2. Íåñîáñòâåííûå èíòåãðàëû
4.2.1. Âû÷èñëèòü èíòåãðàëû èëè óñòàíîâèòü èõ ðàñõîäèìîñòü:
à)
;
)/( arctg)(
22
∫
+∞
⋅+
n
nxxn
dx
á)
∫
+
++−
nm
n
mnxnmx
dx
.
)(
2
4.3. Ïðèìåíåíèÿ îïðåäåëåííûõ èíòåãðàëîâ
4.3.1. Ïîñòðîèòü ñõåìàòè÷åñêèé ÷åðòåæ è íàéòè ïëîùàäü ôè-
ãóðû, îãðàíè÷åííîé ëèíèÿìè:
à) y = õ
2
+ mõ n
2
, (mn + n
2
) x (m + n) y + m
2
n n
3
= 0;
á) (x
2
+ y
2
)
2
= 2 (m + n)
2
xy.
4.3.2. Íàéòè îáúåì òåëà, ïîëó÷åííîãî ïðè âðàùåíèè âîêðóã
îñè ÎÕ ôèãóðû, îãðàíè÷åííîé ëèíèÿìè:
.0 , ,0
2
2
=−−+== mnmnymx
m
x
yy
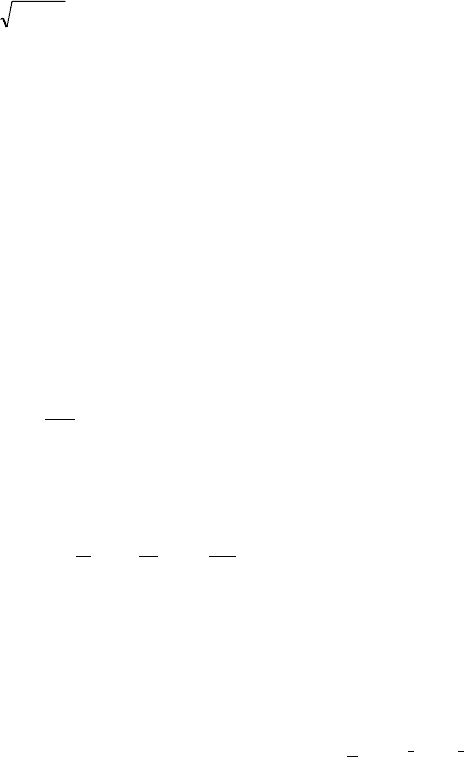
415
4.4. Ïðèáëèæåííîå âû÷èñëåíèå
îïðåäåëåííûõ èíòåãðàëîâ
4.4.1. Äëÿ âû÷èñëåíèÿ îïðåäåëåííîãî èíòåãðàëà
,
5
5
2
∫
+
−
+=
m
m
dxnxJ
ðàçáèâàÿ îòðåçîê èíòåãðèðîâàíèÿ ñíà÷àëà íà
10 ðàâíûõ ÷àñòåé, à çàòåì íà 20 ðàâíûõ ÷àñòåé, íàéòè ïðèáëèæåí-
íûå çíà÷åíèÿ J
10
è J
20
:
à) ïî ôîðìóëå òðàïåöèé;
á) ïî ôîðìóëå Ñèìïñîíà.
Îöåíèòü òî÷íîñòü ïðèáëèæåíèÿ ñ ïîìîùüþ ðàçíîñòè
ε
= | J
10
J
20
|.
5. Ôóíêöèè íåñêîëüêèõ ïåðåìåííûõ
5.1. ×àñòíûå ïðîèçâîäíûå è äèôôåðåíöèàë ôóíêöèè
5.1.1. Íàéòè ÷àñòíûå ïðîèçâîäíûå
xyyx
zzz
′′′′
è ,
ôóíêöèé:
à) z = (x m)
2
· y
n
+ x
m
· (y + n)
3
+ mn;
á)
.
ny
mx
ez
−
−
=
5.1.2. Íàéòè äèôôåðåíöèàë dz ôóíêöèè z = sin
2
(mx
2
ny
2
).
5.1.3. Ïîêàçàòü, ÷òî ôóíêöèÿ z = y · ln (mx
2
ny
2
) óäîâëåòâîðÿ-
åò óðàâíåíèþ
.
2
y
mz
z
y
m
z
x
n
yx
=
′
⋅+
′
⋅
5.2. Ïðèëîæåíèÿ ÷àñòíûõ ïðîèçâîäíûõ
5.2.1. Ñîñòàâèòü óðàâíåíèÿ êàñàòåëüíîé ïëîñêîñòè è íîðìàëè
ê ïîâåðõíîñòè 4z = xy nx my + mn â òî÷êå (m; n; mn).
5.2.2. Äëÿ ôóíêöèè z = ln (mx
2
+ ny
2
) â òî÷êå À (n; m) íàéòè
ãðàäèåíò è ïðîèçâîäíóþ ïî íàïðàâëåíèþ
.jnima ⋅−⋅=
5.2.3. Íàéòè íàèáîëüøåå è íàèìåíüøåå çíà÷åíèÿ ôóíê-
öèè z = 4x
2
+ y
2
4mx ny + m
2
+ n
2
â îáëàñòè, çàäàííîé íåðàâåí-
ñòâàìè: x ≥ 0; nx my ≤ 0; x + y m n ≤ 0.
416
6. Äâîéíûå, òðîéíûå è êðèâîëèíåéíûå
èíòåãðàëû
6.1. Äâîéíûå èíòåãðàëû
6.1.1. Èçìåíèòü ïîðÿäîê èíòåãðèðîâàíèÿ:
à)
∫∫
+
my
nmy
n
dx
y
x
f
d
y
/0
;
),(
á)
∫∫∫∫
−+
+
+
2
)/(
0
/)(
00
.
),( ),(
mxnxnm
nm
m
m
d
y
y
x
f
dxd
y
y
x
f
dx
6.1.2. Ñäåëàòü ÷åðòåæ è íàéòè îáúåì òåëà, îãðàíè÷åííîãî ïî-
âåðõíîñòÿìè z = 0, y = x
2
è ïëîñêîñòüþ, ïðîõîäÿùåé ÷åðåç òî÷êè
À (n; n
2
; 0), B (m; n
2
; 0) è Ñ (0; 0; m + n).
6.1.3. Ñäåëàòü ÷åðòåæ è íàéòè ïëîùàäü ôèãóðû, îãðàíè÷åí-
íîé ëèíèÿìè:
à) y = 0, y = x
2
, ny = m
2
(x m n);
á) õ
2
+ y
2
≥ 6, õ
2
+ y
2
≤ 2nx + 2ny.
6.2. Òðîéíûå èíòåãðàëû
6.2.1. Íàéòè
∫∫∫
V
dzdydxx
,
åñëè òåëî V îãðàíè÷åíî ïëîñêîñòÿ-
ìè x = 0, y = 0, n
2
x + m
2
y mnz = 0 è x + y + z m n = 0.
6.2.2. Íàéòè îáúåì òåëà, îãðàíè÷åííîãî ïîâåðõíîñòÿìè
nz = x
2
+ y
2
, z = n, x = 0, ny = mx.
6.3. Êðèâîëèíåéíûå èíòåãðàëû
6.3.1. Âû÷èñëèòü
∫
+
C
d
y
y
xQdx
y
xP
,
),( ),(
ãäå P (x, y) = ny + 2x, Q (x, y) = mx + 2y, à êîíòóð Ñ îáðàçîâàí
ëèíèÿìè n
2
y = m
2
x
2
, y = m
2
, x = 0:
a) íåïîñðåäñòâåííî;
á) ïî ôîðìóëå Ãðèíà.
417
6.3.2. Âû÷èñëèòü
∫
+−+++
C
zdznmd
y
nz
y
dxmzx
, )( 2 )2( )2(
ãäå êîíòóð Ñ ÿâëÿåòñÿ îäíèì âèòêîì âèíòîâîé ëèíèè:
+=
≤≤=
=
, )(
20),( sin
),( cos
.
tnmz
tmtny
mtnx
π
7. Ýëåìåíòû òåîðèè ïîëÿ
7.1. Äèôôåðåíöèàëüíûå îïåðàöèè
7.1.1. Íàéòè â òî÷êå À (n; m; 0) ãðàäèåíò ñêàëÿðíîãî ïîëÿ
.
nymx
nmz
u
+
++
=
7.1.2. Íàéòè â òî÷êå B (n; m; m + n) äèâåðãåíöèþ âåêòîðíîãî
ïîëÿ
. )( ) , ,(
22
2222
kznmj
x
nyz
i
y
mxz
zyxF ⋅++⋅
−
+⋅
−
=
7.1.3. Íàéòè â òî÷êå Ñ (m; n; 1) ðîòîð âåêòîðíîãî ïîëÿ
. )( ) , ,( kznymxj
z
nymx
i
z
mynx
zyxF ⋅+−
−
+⋅
−
=
7.2. Èíòåãðàëû è èíòåãðàëüíûå òåîðåìû
7.2.1. Óáåäèòüñÿ, ÷òî ïîëå
knymxjnzimzzyxF ⋅++⋅+⋅= )(),,(
ïîòåíöèàëüíî, è íàéòè åãî ïîòåíöèàë.
7.2.2. Äàíû ïîëå
kxynmjmznxinzmyF ⋅++⋅−+⋅−= )()()(
2222
è ïèðàìèäà ñ âåðøèíàìè O (0; 0; 0), A (m; 0; 0), B (0; n; 0),
Ñ (0; 0; m + n). Íàéòè:
à) ïîòîê ïîëÿ
F
÷åðåç ãðàíü ÀÂÑ ïèðàìèäû â íàïðàâëåíèè
íîðìàëè, ñîñòàâëÿþùåé îñòðûé óãîë ñ îñüþ ÎZ;
418
á) ïîòîê ïîëÿ
F
÷åðåç âíåøíþþ ïîâåðõíîñòü ïèðàìèäû ñ ïî-
ìîùüþ òåîðåìû Îñòðîãðàäñêîãî Ãàóññà;
â) öèðêóëÿöèþ ïîëÿ
F
âäîëü çàìêíóòîãî êîíòóðà ÀÂÑ:
â
1
) íåïîñðåäñòâåííî;
â
2
) ñ ïîìîùüþ òåîðåìû Ñòîêñà (îáõîä êîíòóðà ïðîèñõî-
äèò â ïîëîæèòåëüíîì íàïðàâëåíèè îòíîñèòåëüíî âíåø-
íåé íîðìàëè ê ïîâåðõíîñòè ïèðàìèäû).
8. Äèôôåðåíöèàëüíûå óðàâíåíèÿ
8.1. Óðàâíåíèÿ ïåðâîãî ïîðÿäêà
8.1.1. Íàéòè îáùåå ðåøåíèå óðàâíåíèÿ:
à) y ′ = e
mx ny
;
á) (nx my) · y ′ = mx + ny;
â)
;
arctg)(
22
m
x
nyyxm =+
′
⋅+
ã)
.
12
+
⋅=+
′
n
y
x
x
m
y
y
8.1.2. Ñêîðîñòü ðîñòà áàíêîâñêîãî âêëàäà ïðîïîðöèîíàëü-
íà ñ êîýôôèöèåíòîì ðàâíûì m âåëè÷èíå âêëàäà. Íàéòè çàêîí èç-
ìåíåíèÿ âåëè÷èíû âêëàäà ñî âðåìåíåì, åñëè ïåðâîíà÷àëüíàÿ ñóì-
ìà âêëàäà ñîñòàâëÿëà n ìèëëèîíîâ ðóáëåé.
8.2. Ëèíåéíûå óðàâíåíèÿ âûñøèõ ïîðÿäêîâ
8.2.1. Ðåøèòü çàäà÷ó Êîøè:
à) y ′″ (m n) · y″ mn · y ′ = 0, y (0) = 0, y ′ (0) = m, y″ (0) = n;
á) y ″ 2n · y ′ + n
2
y = (x + m) · e
(m + n)x
, y (0) = m, y ′ (0) = n;
â) y ″ + n
2
y = sin (mx), y (0) = 0, y ′ (0) = m + n.
8.3. Ñèñòåìû ëèíåéíûõ óðàâíåíèé
8.3.1. Ðåøèòü ñèñòåìó ëèíåéíûõ óðàâíåíèé
+=
−=
,
,
mynx
dt
dy
nymx
dt
dx
ñ íà÷àëüíûìè óñëîâèÿìè x (0) = 1, y (0) = 2.
419
9. Ðÿäû
9.1. ×èñëîâûå ðÿäû
9.1.1. Èññëåäîâàòü íà ñõîäèìîñòü ðÿäû ñ ïîëîæèòåëüíûìè ÷ëå-
íàìè:
à)
;
21
3
1
2
2
∑
∞
=
+−
+−
k
nkk
nkmk
á)
;
23
12
1
∑
∞
=
+
+
+
+
k
mk
nk
â)
∑
∞
=
+⋅+
+⋅
1
2
2
;
)(
k
k
mknm
nkm
ã)
∑
∞
=
++
1
.
1)1(
! )(
k
k
n
mk
9.2. Ñòåïåííûå ðÿäû
9.2.1. Íàéòè îáëàñòü ñõîäèìîñòè ñòåïåííîãî ðÿäà:
à)
;
12
2
1
∑
∞
=
+
⋅
k
nk
kmk
x
á)
;
)(
23
12
1
1
∑
∞
=
+
−⋅
+⋅
+⋅
k
k
m
m
nx
k
k
â)
.
! )(
2
1
∑
∞
=
⋅
k
knk
mk
x
9.2.2. Ðàçëîæèòü ôóíêöèþ f (õ) â ðÿä Òåéëîðà â îêðåñòíîñòè
òî÷êè õ
0
:
à)
; ,
0
)(
nx
mx
x
xf
=
+
=
á)
∫
=
−
=
nx
m
x
x
dx
xf
0
.0
0
,
1
)(
9.2.3. Ñ ïîìîùüþ ðàçëîæåíèÿ â ðÿä âû÷èñëèòü ïðèáëèæåííî ñ
òî÷íîñòüþ 0,001 çíà÷åíèÿ:
à) å
n
;
á)
.
)( sin
0
2
dx
x
x
nm
n
∫
+
9.3. Ðÿäû Ôóðüå
9.3.1. Ðàçëîæèòü ôóíêöèþ f (õ) â ðÿä Ôóðüå â óêàçàííîì èí-
òåðâàëå: f (õ) = (x m)
2
â èíòåðâàëå (0, m).

420
10. Ôóíêöèè êîìïëåêñíîãî ïåðåìåííîãî
10.1. Äåéñòâèÿ ñ êîìïëåêñíûìè ÷èñëàìè
10.1.1. Âûïîëíèòü äåéñòâèÿ:
à) (m + in)
2
· (n im);
á)
.
imn
inm
+
−
10.2. Àíàëèòè÷åñêèå ôóíêöèè
10.2.1. Ïîêàçàòü, ÷òî ôóíêöèÿ f (z) = (z + m)
2
+ z ni
àíàëèòè÷íà.
10.3. Èíòåãðèðîâàíèå ôóíêöèé
êîìïëåêñíîãî ïåðåìåííîãî
10.3.1. Âû÷èñëèòü
∫
++−
C
dzmyxiynx , ))( )((
ãäå êîíòóð Ñ
íåçàìêíóòàÿ ëîìàíàÿ, ñîåäèíÿþùàÿ òî÷êè Î (0, 0), À (m, n)
è B (0, m + n).
10.4. Ðÿäû Òåéëîðà è Ëîðàíà
10.4.1. Ðàçëîæèòü ôóíêöèþ
mnmznmz
z
zf
+++−
=
22
)2(
)(
â îêðåñòíîñòè òî÷êè z
0
= 0 â ðÿä Òåéëîðà è íàéòè ðàäèóñ ñõîäèìî-
ñòè ðÿäà.
10.5. Âû÷åòû è èõ ïðèëîæåíèÿ
10.5.1. Îïðåäåëèòü òèï îñîáûõ òî÷åê ôóíêöèè
23
1
)(
nzz
zf
+
=
è íàéòè âû÷åòû â íèõ.
11. Ïðèëîæåíèÿ îïåðàöèîííîãî èñ÷èñëåíèÿ
11.1. Ðåøèòü îïåðàöèîííûì ìåòîäîì äèôôåðåíöèàëüíîå óðàâ-
íåíèå:
x″ + (m n)x′ mnx = e
(mn)t
, x(0) = 0, x′(0) = m.
