Шапкин А.С., Шапкин В.А. Задачи по высшей математике, теории вероятностей, математической статистике, математическому программированию с решениями
Подождите немного. Документ загружается.

81
Îñíîâíûå ïðàâèëà äèôôåðåíöèðîâàíèÿ
Ïóñòü Ñ ïîñòîÿííàÿ, u(x), v(x) äèôôåðåíöèðóåìûå â òî÷êå õ
ôóíêöèè.
1. C′ = 0;
2. x′ = 1;
3. (u ± v)′ = u′ ± u′;
4. (cu)′ = cu′;
5. (uv)′ = u′v + uv′;
6.
,
2
v
vuvu
v
u
′
−
′
=
′
v ≠ 0;
7. Åñëè y = f(u), ãäå u = u(x), (òî åñòü y = f(u(x)) ñëîæíàÿ
ôóíêöèÿ îò õ) è ôóíêöèè f (u) è u(x) äèôôåðåíöèðóåìû, òî ïðîèç-
âîäíàÿ ñëîæíîé ôóíêöèè y = f (u(x)) âû÷èñëÿåòñÿ ïî ôîðìóëå
.
xux
ufy
′
⋅
′
=
′
8. Åñëè ôóíêöèÿ àðãóìåíòà õ çàäàíà ïàðàìåòðè÷åñêè
=
=
),(
)(
ty
tx
ψ
ϕ
òî
dt
dx
dt
dy
y
x
=
′
èëè
.
t
t
x
x
y
y
′
′
=
′
Îïðåäåëåíèå. Äèôôåðåíöèàëîì ôóíêöèè y = f(x) íàçûâàåòñÿ
ãëàâíàÿ ÷àñòü åå ïðèðàùåíèÿ, ëèíåéíàÿ îòíîñèòåëüíî ïðèðàùåíèÿ
àðãóìåíòà, òî åñòü, åñëè ∆y = f ′(x)∆x +
α
(∆x) · ∆x, ãäå
α
(∆x) → 0
áåñêîíå÷íî ìàëàÿ ôóíêöèÿ ïðè ∆x → 0, òî äèôôåðåíöèàë ôóíê-
öèè dy = f ′(x)dx.
Äèôôåðåíöèàë íåçàâèñèìîãî àðãóìåíòà ðàâåí ïðèðàùåíèþ àð-
ãóìåíòà, òî åñòü dx = ∆x. Ñëåäîâàòåëüíî, dy = f ′ (x) · dx.
Åñëè ∆x ìàëî, òî ∆y ≈ dy, è, ñëåäîâàòåëüíî, f(x + ∆x) ≈ f (x) + dy =
= f(x) + f ′(x)dx (ôîðìóëà ïðèáëèæåííîãî âû÷èñëåíèÿ ñ ïîìîùüþ
äèôôåðåíöèàëà).
Ïðèìåð 2.11. Íàéòè ïðîèçâîäíûå äàííûõ ôóíêöèé:
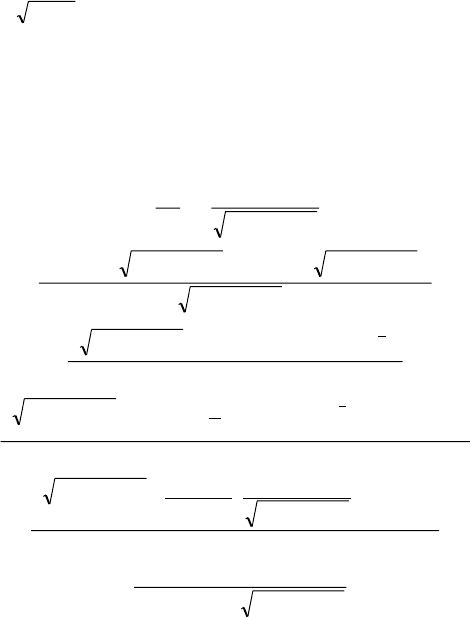
à)
;
43
63
2
xx
x
y
+−
+
=
82
á) y = sin
2
(x cosx
3
);
â)
;ln
3
xxy =
ã) y = x
tgx
;
ä) x
3
+ y
3
3xy = 0.
Ðåøåíèÿ:
à) ïðèìåíèì òåîðåìó î ïðîèçâîäíîé ÷àñòíîãî:
;
43)43(
1524
43
)24(
43
1
2
)63(
436
43
)43()43(
2
1
)63(436
43
))43)((63(436
)43(
)43)(63(43)63(
43
63
22
2
2
2
2
222
2
22
22
22
2
2
1
2
1
xxxx
õ
xx
õ
xx
x
xx
xx
xxxxxxx
xx
xxxxx
xx
xxxxxx
xx
x
dx
dy
y
+−+−
−
=
=
+−
+−⋅
+−
⋅
+
−+−
=
=
+−
′
+−⋅+−⋅+−+−
=
=
+−
′
+−+−+−
=
=
+−
′
+−+−+−⋅
′
+
=
=
′
+−
+
==
′
−
á) ïðèìåíèì òåîðåìû î ïðîèçâîäíîé ïðîèçâåäåíèÿ è ïðîèç-
âîäíîé ñëîæíîé ôóíêöèè:
);3sin)(coscos(2sin
))(sin)(coscos(2sin
))(coscos()cos(2sin
)cos()coscos()cossin(2
))cos(sin()cossin(2
2333
3333
333
333
33
xxxxxx
xxxxxx
xxxxxx
xxxxxx
xxxxy
⋅−=
=
′
−=
=
′
+
′
⋅=
=
′
⋅⋅=
=
′
⋅=
′

83
â)
);
1
(ln)ln(
3
1
))(lnln()ln(
3
1
)ln()ln(
3
1
)ln(
3
2
3
2
3
2
3
1
x
xxxxxxxxxx
xxxxxxy
⋅+=
′
+
′
⋅=
=
′
⋅=
′
=
′
−−
−
ã) ïðîëîãàðèôìèðóåì îáå ÷àñòè ðàâåíñòâà:
,lntgln;lnln
tg
xxyxy
x
⋅−==
−
ó÷èòûâàÿ, ÷òî ó ÿâëÿåòñÿ ôóíêöèåé îò õ, íàéäåì ïðîèçâîäíûå îáå-
èõ ÷àñòåé ðàâåíñòâà:
.)lntg()(ln
′
⋅−=
′
xxy
;
tg
cos
lntg
cos
ln
;
1
tgln
cos
1
2
tg
2
2
+−=
+−=
′
⋅−⋅−=
′
−
x
x
x
x
x
x
x
x
x
yy
x
xx
x
y
y
x
ä) ôóíêöèÿ çàäàíà íåÿâíî. Äëÿ òîãî, ÷òîáû íàéòè y ′, ïðî-
äèôôåðåíöèðóåì îáå ÷àñòè ðàâåíñòâà ïî õ, ñ÷èòàÿ ó ôóíêöèåé îò
x(y = y(x)), à çàòåì ðàçðåøèì óðàâíåíèå îòíîñèòåëüíî y ′:
(x
3
+ y
3
3yx)′ = 0′; 3x
2
+ 3y
2
y ′ 3(y + xy ′) = 0;
y ′(3y
2
3x) = 3y 3x
2
;
.
33
33
2
2
2
2
xy
xy
xy
xy
y
−
−
=
−
−
=
′
Ïðèìåð 2.12. Íàéòè ïðîèçâîäíóþ ôóíêöèé:
à)
;)623(
4
3
25
+−= xxy
;
3
4
15)623(4
]0)(2)(3[)623(4
])6()2()3[()623(4
)623()623(4])623[(
3
1
3
2
3
2
43
3
25
53
3
25
53
3
25
3
2514
3
254
3
25
−⋅+−=
=+
′
−
′
+−=
=
′
+
′
−
′
+−=
=
′
+−⋅+−=
′
+−=
′
−
−
xxxx
xxxx
xxxx
xxxxxxy
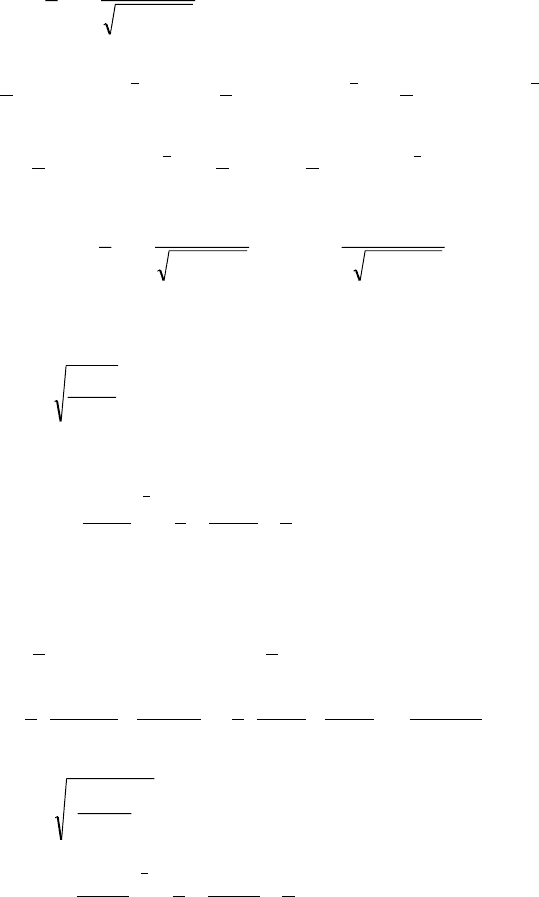
84
á)
.
)2(
1
2
1
6
3
42
6
+
−=
x
xy
)
.
)2(3
8
3
)2(
1
2
1
6
)2()2(
3
4
6
2
1
)2(
2
1
6
)2(
2
1
)2(
2
1
6)2(
2
1
3
72
5
5
3
42
6
225
5
26
26
5
26
6
26
3
7
3
4
3
4
3
4
3
4
+
+⋅
+
−=
=
′
+
⋅+⋅
−−⋅
+−=
=
′
+−⋅
+−=
′
+−=
′
−−
−−−
x
x
x
x
x
xxxxx
xxxxxxy
Ïðèìåð 2.13. Íàéòè ïðîèçâîäíóþ ôóíêöèé:
à)
.
1
1
ln
3
4
4
x
x
y
+
−
=
Èñïîëüçóÿ ñâîéñòâà ëîãàðèôìîâ, óïðîñòèì
()
.)1ln()1ln(
3
1
1
1
ln
3
1
1
1
ln
44
4
4
4
4
3
1
xx
x
x
x
x
y +−−=
+
−
=
+
−
=
Íàõîäèì ïðîèçâîäíóþ
()()()
;
)1(3
8
1
4
1
4
3
1
1
)1(
1
)1(
3
1
)1ln()1ln(
3
1
)1ln()1ln(
3
1
8
3
4
3
4
3
4
4
4
4
4444
−
−=
+
−
−
−
=
+
+
−
−
′
−
=
=
′
+−
′
−=
′
+−−=
′
x
x
x
x
x
x
x
x
x
x
xxxxy
á)
.
2
61
ln
9
2
3
+
−
=
x
x
y
Ïðåîáðàçóåì ôóíêöèþ
()
.)2ln()61ln(
9
2
2
61
ln
9
2
2
61
ln
3
33
9
2
xx
x
x
x
x
y +−−=
+
−
=
+
−
=
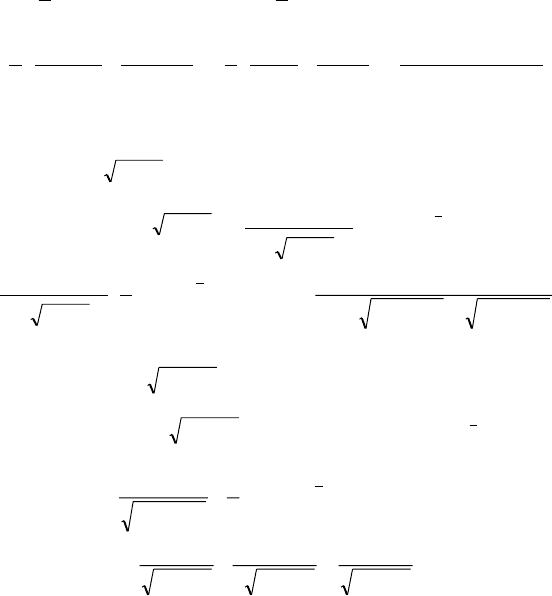
85
Äèôôåðåíöèðóåì
()
.
)2)(61(3
)44(2
2
3
61
6
9
2
2
)2(
61
)61(
9
2
]))2(ln())61[(ln(
9
2
)2ln()61ln(
9
2
3
32
3
2
3
3
33
xx
xx
x
x
x
x
x
x
x
xxxxy
+−
−+−
=
+
−
−
−
=
+
′
+
−
−
′
−
=
=
′
+−
′
−=
′
+−−=
′
Ïðèìåð 2.14. Íàéòè ïðîèçâîäíóþ ôóíêöèé:
à)
.21tgarc
3
xy −=
Äèôôåðåíöèðóåì
()
()
()
;
)21())21(1(3
2
)21()21(
3
1
211
1
)21(
211
1
21arctg
3
2
3
2
1
2
3
2
3
3
3
1
3
1
xx
xx
x
x
x
xy
−⋅−+
−
=
′
−⋅−⋅
−+
=
=
′
−⋅
−+
=
′
−=
′
−
á)
.412arcsin
2
xxy −−=
Äèôôåðåíöèðóåì
()
.
41
)21(2
412
8
41
2
)41()41(
2
1
)2(1
)2(
)41(2arcsin412arcsin
222
2
1
2
2
22
2
1
2
1
x
x
x
x
x
xx
x
x
xxxxy
−
+
=
−
−
−
−
=
=
′
−⋅−−
−
′
=
=
′
−−
′
=
′
−−=
′
−
Ìåõàíè÷åñêèé ñìûñë ïðîèçâîäíîé
Åñëè ïðè ïðÿìîëèíåéíîì äâèæåíèè òî÷êè çàäàí çàêîí
äâèæåíèÿ S = s(t), òî ñêîðîñòü äâèæåíèÿ â ìîìåíò t
0
åñòü ïðîèç-
âîäíàÿ ïóòè ïî âðåìåíè:
v = s ′(t
0
).
Ïðèìåð 2.15. Êàêîé óãîë îáðàçóåò ñ îñüþ àáñöèññ êàñàòåëü-
íàÿ ê êðèâîé y = x
3
+ 4x
2
, ïðîâåäåííàÿ â òî÷êå Ì
0
(1; 5). Íàïèñàòü
óðàâíåíèÿ êàñàòåëüíîé è íîðìàëè, ïðîâåäåííûõ ê êðèâîé â äàí-
íîé òî÷êå.
86
Äëÿ îïðåäåëåíèÿ óãëîâîãî êîýôôèöèåíòà êàñàòåëüíîé íàõî-
äèì ïðîèçâîäíóþ îò çàäàííîé ôóíêöèè:
f ′(x) = 3x
2
+ 8x.
Äàëåå îïðåäåëÿåì ÷èñëåííîå çíà÷åíèå ïðîèçâîäíîé â òî÷êå
Ì
0
(1; 5), äëÿ ýòîãî ïîäñòàâëÿåì â âûðàæåíèå ïðîèçâîäíîé
x = 1:
f ′(1) = 3(1)
2
+ 8(1) = 11.
Çíà÷åíèå ïðîèçâîäíîé ïðè x = 1 è äàåò èñêîìûé óãëîâîé êî-
ýôôèöèåíò k = 11, ò.å. tg
α
= 11, îòêóäà
α
= arc tg (11) ≈ 84°50′.
Äëÿ ñîñòàâëåíèÿ óðàâíåíèÿ êàñàòåëüíîé èñïîëüçóåì ôîð-
ìóëó y y
0
= f ′(x
0
)(x x
0
):
y 5 = 11(x 1) èëè 11x y 6 = 0.
Äëÿ ñîñòàâëåíèÿ óðàâíåíèÿ íîðìàëè ïîëüçóåìñÿ ôîðìóëîé
:)(
)(
1
0
0
0
xx
xf
yy −
′
−=−
)1(
11
1
5 −−=− xy
èëè x + 11y 56 = 0.
Ïðèìåð 2.16. Îïðåäåëèòü, ïîä êàêèì óãëîì êðèâàÿ
2
1
1
x
x
y
+
−
=
ïåðåñåêàåò îñü àáñöèññ.
Íàõîäèì òî÷êó ïåðåñå÷åíèÿ êðèâîé
2
1
1
x
x
y
+
−
=
ñ îñüþ OX, óðàâ-
íåíèå êîòîðîé ó = 0, ò.å. ðåøàåì ñèñòåìó:
,0
1
1
,
0
1
1
2
2
=
+
−
⇒
=
+
−
=
x
x
y
x
x
y
îòêóäà ïîëó÷àåì õ = 1.
Ïîä óãëîì äàííîé êðèâîé ñ îñüþ OX ïîíèìàåòñÿ óãîë, êî-
òîðûé êàñàòåëüíàÿ ê ýòîé êðèâîé â òî÷êå õ = 1 îáðàçóåò ñ îñüþ

87
àáñöèññ. Íàéäåì óãëîâîé êîýôôèöèåíò êàñàòåëüíîé ê êðèâîé â
òî÷êå õ = 1:
,
2
1
)11(
211
)1(
21
)1(
)1(21
1
1
tg
2
1
22
2
1
22
2
2
=
+
+−
=
+
+−
=
=
+
−−+
=
′
+
−
=
′
=
=
=
x
x
x
xx
x
xxx
x
x
y
α
îòêóäà
.4326
2
1
tgarc
′
≈=
o
α
Ïðèìåð 2.17. Ïîä êàêèì óãëîì ïåðåñåêàþòñÿ ïàðàáîëû
y = 4 + 6x x
2
è y = (x 2)
2
?
Ðåøàÿ ñîâìåñòíî óðàâíåíèÿ ïàðàáîë, íàõîäèì àáñöèññû èõ
òî÷åê ïåðåñå÷åíèÿ:
.4,1
;045
;64)2(
,64
,)2(
21
2
22
2
2
==
=+−
−+−=−
−+−=
−=
xx
xx
xxx
xxy
xy
Îïðåäåëÿåì, ÷òî òî÷êè ïåðåñå÷åíèÿ ïàðàáîë, ñîîòâåòñòâóþùèå
íàéäåííûì àáñöèññàì ýòî òî÷êè À(1; 1) è B(4; 4) (ðèñ. 23).
õ = 1 õ = 1
Ðèñ. 23
y
B
A
ϕ
2
ϕ
1
<
<
x
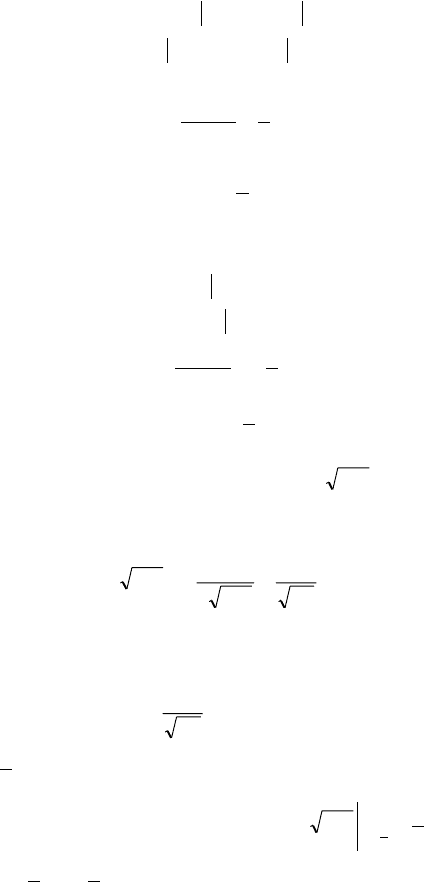
88
Íàõîäèì óãëîâûå êîýôôèöèåíòû êàñàòåëüíûõ ê ïàðàáîëàì â
òî÷êå À:
.2)2(2])2[(
,426)64(
11
2
2
11
2
1
−=−=
′
−=
=−=
′
−+−=
==
==
xx
xx
xxk
xxxk
Âû÷èñëÿåì òàíãåíñ óãëà ìåæäó êàñàòåëüíûìè:
,
7
6
421
42
tg
1
=
⋅−
−−
=
ϕ
îòêóäà
.
7
6
tgarc
1
=
ϕ
Òàêæå îïðåäåëÿåì óãîë ìåæäó êðèâûìè â òî÷êå Â:
.
7
6
tg arc
,
7
6
241
24
tg
,4)2(2
,226
2
2
42
41
−=
−=
⋅−
+
=
=−=
−=−=
=
=
ϕ
ϕ
x
x
xk
xk
Ïðèìåð 2.18.  êàêîé òî÷êå ïàðàáîëû
xy 18=
îðäèíàòà âîç-
ðàñòàåò âäâîå áûñòðåå, ÷åì àáñöèññà?
Íàéäåì ïðîèçâîäíóþ îò çàäàííîé ôóíêöèè:
()
.
2
3
182
18
18
xx
xy ==
′
=
′
Òàê êàê ïðîèçâîäíàÿ õàðàêòåðèçóåò ñêîðîñòü âîçðàñòàíèÿ îð-
äèíàòû (ôóíêöèè) ïî ñðàâíåíèþ ñ âîçðàñòàíèåì àðãóìåíòà, òî èç
óñëîâèÿ çàäà÷è èìååì:
,2
2
3
=
x
îòñþäà
8
9
=x
àáñöèññà èñêîìîé òî÷êè.
À îðäèíàòà íàõîäèòñÿ èç óðàâíåíèÿ
.
2
9
18
8
9
==
=
x
xy
Îòâåò:
.
2
9
,
8
9
== yx

89
Ïðîèçâîäíûå âûñøèõ ïîðÿäêîâ
Îïðåäåëåíèå. Ïðîèçâîäíîé âòîðîãî ïîðÿäêà (èëè âòîðîé ïðî-
èçâîäíîé) îò ôóíêöèè y = f(x) íàçûâàåòñÿ ïðîèçâîäíàÿ îò åå ïðî-
èçâîäíîé, ò.å. y″ = (y′)′.
Îáîçíà÷àåòñÿ âòîðàÿ ïðîèçâîäíàÿ òàê:
y″ èëè
,
2
2
dx
yd
èëè f ″(x).
Åñëè s = f (t) çàêîí ïðÿìîëèíåéíîãî äâèæåíèÿ òî÷êè, òî
2
2
dt
sd
åñòü óñêîðåíèå ýòîãî äâèæåíèÿ. Àíàëîãè÷íî, ïðîèçâîäíàÿ òðåòüåãî
ïîðÿäêà ôóíêöèè y = f (x) åñòü ïðîèçâîäíàÿ îò ïðîèçâîäíîé âòî-
ðîãî ïîðÿäêà y′″ = (y″)′.
Âîîáùå, ïðîèçâîäíîé n-ãî ïîðÿäêà îò ôóíêöèè y = f (x) íàçû-
âàåòñÿ ïðîèçâîäíàÿ îò ïðîèçâîäíîé (n 1)-ãî ïîðÿäêà:
)(
)1()(
′
=
−
nn
yy
.
Äëÿ n-îé ïðîèçâîäíîé óïîòðåáëÿþòñÿ îáîçíà÷åíèÿ:
y
(n)
èëè
,
n
n
dx
y
d
èëè f
(n)
(x).
Ïðîèçâîäíûå âûñøèõ ïîðÿäêîâ (âòîðàÿ, òðåòüÿ è ò.ä.) âû-
÷èñëÿþòñÿ ïîñëåäîâàòåëüíûì äèôôåðåíöèðîâàíèåì äàííîé
ôóíêöèè.
Ïðèìåð 2.19. y = (arc tg x). Íàéòè ó″.
Íàõîäèì ïåðâóþ ïðîèçâîäíóþ:
.
1
1
2
x
y
+
=
′
Âòîðàÿ ïðîèçâîäíàÿ, ïî îïðåäåëåíèþ, ðàâíà ïðîèçâîäíîé îò
ïåðâîé ïðîèçâîäíîé, ñëåäîâàòåëüíî:
[][ ]
.
)1(
2
)1()1()1(
1
1
22
22212
2
x
x
xxx
x
y
+
−=
′
++−=+=
′
+
=
′′
−−
90
Ïðèìåð 2.20. Íàéòè y′″(3), åñëè f (x) = (2x 3)
5
.
Íàõîäèì ïîñëåäîâàòåëüíî ïåðâóþ, âòîðóþ è òðåòüþ ïðîèçâîäíûå:
f ′(x) = [(2x 3)
5
]′ = 5(2x 3)
4
· 2 = 10(2x 3)
4
,
f ′′(x) = 10 · 4(2x 3)
3
· 2 = 80(2x 3)
3
,
f ′′′(x) = 80 · 3 · (2x 3)
2
· 2 = 480(2x 3)
2
.
Ïîäñòàâëÿÿ â òðåòüþ ïðîèçâîäíóþ çíà÷åíèå õ = 3, ïîëó÷èì:
f ′′′(3) = 480(2 · 3 3)
2
= 4320.
Ïðèìåð 2.21. Íàéòè y′′′′îò ôóíêöèè y = sin2x.
Íàõîäèì ïîñëåäîâàòåëüíî ïåðâóþ, âòîðóþ, òðåòüþ è ÷åòâåð-
òóþ ïðîèçâîäíûå:
y′ = 2cos2x,
y′′ = 4sin2x,
y′′′ = 8cos2x,
y′′′′ = 16sin2x.
Ïðèìåð 2.22. Ïîêàçàòü, ÷òî ôóíêöèÿ y = å
2õ
· sin5x óäîâëåòâî-
ðÿåò äèôôåðåíöèàëüíîìó óðàâíåíèþ:
y′′ 4y′ + 29y = 0.
Íàéäåì ïåðâóþ è âòîðóþ ïðîèçâîäíûå îò ôóíêöèè
y = å
2õ
· sin5x:
y′ = 2å
2õ
· sin5x + 5å
2õ
· cos5x,
y′′ = 2(2å
2õ
· sin5x + 5å
2õ
· cos5x) + 5(2å
2õ
· cos5x 5å
2õ
· sin5x) =
= 20å
2õ
· cos5x 21å
2õ
· sin5x.
Ïîäñòàâèì íàéäåííûå âûðàæåíèÿ äëÿ y′ è y′′ â äàííîå óðàâíå-
íèå è ïîëó÷èì òîæäåñòâî:
20å
2õ
· cos5x 21å
2õ
· sin5x 4(2å
2õ
· sin5x + 5å
2õ
· cos5x) +
+ 29 · e
2x
· sin5x = 0, 0 = 0.
Äèôôåðåíöèðîâàíèå íåÿâíûõ ôóíêöèé
Îïðåäåëåíèå. Åñëè çàâèñèìîñòü ó îò x çàäàåòñÿ ïîñðåäñòâîì
ñîîòíîøåíèÿ F(x, y) = 0, ãäå F(x, y) âûðàæåíèå, ñîäåðæàùåå
x è ó, òî ó íàçûâàåòñÿ íåÿâíîé ôóíêöèåé îò x. Äëÿ îïðåäåëå-
íèÿ ïðîèçâîäíîé îò íåÿâíî çàäàííîé ôóíêöèè íóæíî îáå ÷àñ-
