Siebertz K., Bebber D., Hochkirchen T. Statistische Versuchsplanung: Design of Experiments (DoE)
Подождите немного. Документ загружается.


5.3 Robustes Design 145
A B C D
− − − −
+ − − +
− + − +
+ + − −
− − + +
+
− + −
− + + −
+ + + +
N
C
+ − − +
N
B
− − + +
N
A
− + − +
y
11
y
12
y
13
y
14
y
21
y
22
y
23
y
24
y
31
y
32
y
33
y
34
y
41
y
42
y
43
y
44
y
51
y
52
y
53
y
54
y
61
y
62
y
63
y
64
y
71
y
72
y
73
y
74
y
81
y
82
y
83
y
84
Leistung Streuung
L
1
S
1
L
2
S
2
L
3
S
3
L
4
S
4
L
5
S
5
L
6
S
6
L
7
S
7
L
8
S
8
.
Tabelle 5.5 Transformation des Ergebnisfeldes zu zwei unabhängigen Qualitätsmerkmalen. Ein
Merkmal beschreibt die Systemleistung, zum Beispiel als Mittelwert der Ergebnisse für eine Steu-
ergrößenkombination. Das zweite Merkmal beschreibt die Streuung, verursacht durch die verschie-
denen Einstellungen des äußeren Feldes. Welche Transformation besonders günstig ist, hängt vom
Einzelfall ab.
Nulldurchgänge zu finden. Bei einigen Anwendungsfällen
4
beschreibt der Null-
durchgang den perfekten Auslegungspunkt.
5.3.2 Toleranzdesign
Strikte Kundenorientierung zeichnet viele erfolgreiche Qualitätsmethoden aus. To-
leranzdesign macht dabei keine Ausnahme und ersetzt die traditionelle bauteilori-
entierte Sichtweise durch eine klare Fokussierung auf die Systemleistung. Letztlich
dient jede Einengung der Bauteiltoleranzen nur dazu, die Streuung der Systemleis-
tung zu reduzieren. Wirkt sich eine Bauteiltoleranz nicht auf die Streuung der Sys-
temleistung aus, macht die Toleranzeinengung keinen Sinn, denn der Kunde merkt
nichts davon. Wenn sich hingegen eine reduzierte Streuung der Systemleistung ein-
stellt, steigt der Marktwert des Produkts, denn in fast allen Fällen erhöht sich da-
durch auch der Gebrauchswert, was der Kunde unmittelbar feststellt.
Der Mehrwert eines Produkts schafft finanziellen Spielraum für die Einengung
der Bauteiltoleranzen. Die Entscheidung wird also immer auf einer sorgfältigen
Kosten-Nutzen-Analyse beruhen. Erst durch die Quantifizierung des Nutzens in
Form einer Wertsteigerung ist diese Analyse möglich. Außerdem erzeugt die Ab-
4
Im einfachsten Fall besteht das äußere Feld aus zwei Einstellungen: ideal, mit Störung. Das
die Streuung beschreibende Qualitätsmerkmal ist dann lediglich die Differenz aus den bei-
den Ergebnissen bei gleicher Steuergrößenkombination. Diese Differenz soll bei optimaler
Auslegung verschwinden (Nulldurchgang) und kann durchaus ihr Vorzeichen wechseln.
146 5 Varianten der statistischen Versuchsplanung
7 8 9 10 11 12 13
4
6
8
10
12
14
16
normierte Streubereiche der Designvariablen (±3σ)
Streubereich des Qualit
¨
atsmerkmals
Faktor mit großem Einfluß
Faktor mit geringem Einfluß
.
.
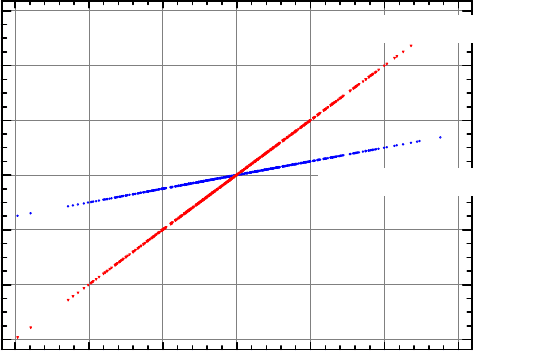
Abb. 5.10 Fiktives Beispiel für die Auswirkung mehrerer Toleranzen auf die Streuung des Quali-
tätsmerkmals. Die Abszisse ist normiert aufgetragen, denn die untersuchten Streuungen der jewei-
ligen Faktoren können durchaus völlig unterschiedliche physikalische Einheiten haben.
bildung auf die Streuung der Systemleistung einen einheitlichen Maßstab für alle
untersuchten Faktoren. Bei bauteilorientierten Toleranzenfestlegungen gelingt dies
nicht.
Die konkrete Anwendung erfolgt völlig analog zur herkömmlichen Versuchs-
planung, allerdings mit sehr kleinen Stufenabständen, entsprechend den zunächst
festgelegten Bauteiltoleranzen. Wegen der geringen Stufenabstände sind nur gerin-
ge Kontraste zu erwarten. Das Qualitätsmerkmal verändert sich also in einem sehr
schlecht messbaren, geringem Umfang. Dies macht bei realen Versuchen immer
eine Messmittelfähigkeitsanalyse erforderlich. Berechnungsverfahren sind hier im
Vorteil, weil in der Regel die Rundungsfehler weit unter den Kontrasten liegen.
Die Aufteilung der Gesamtvarianz V
ges
ergibt sich aus der additiven Überlage-
rung der Teilvarianzen. Zunächst produziert jeder untersuchte Faktor einen Varianz-
anteil V
i
. Die Auswertung der Versuchsreihe wird eine Restvarianz V
R
aufzeigen,
die durch eventuelle Versuchsstreuung, unkontrolliert schwankende Parameter und
eine begrenzte Genauigkeit des Beschreibungsmodells zu erklären ist. Möglicher-
weise wurden signifikante Parameter nicht im Rahmen der Versuchsreihe variiert.
Diese schwanken dann entweder unkontrolliert oder es ist gelungen, sie im Rah-
men der Versuchsreihe konstant zu halten. In jedem Fall treiben sie in der Realität
die Gesamtvarianz des Qualitätsmerkmals nach oben, also kommt zu den genannten
Termen noch ein unbekannter Varianzanteil V
u
hinzu.
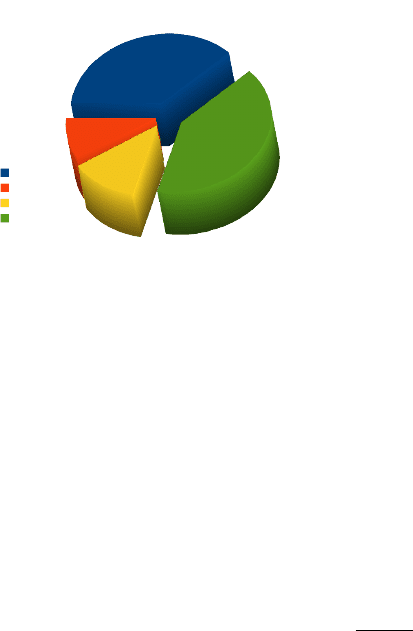
5.3 Robustes Design 147
Faktor A
Faktor B
Faktor C
Rest
Abb. 5.11 Beispiel für die Aufteilung der Ge-
samtvarianz. Die Varianzanalyse zeigt auf, wel-
che Anteile den jeweiligen Faktoren zuzuordnen
sind. Der verbleibende Rest wurde nicht durch
die untersuchten Faktoren erzeugt. Eine Tole-
ranzeinengung kann nur den jeweiligen Varian-
zanteil günstig beeinflussen. Daraus ergibt sich
das Verbesserungspotential in Bezug auf die Sys-
temleistung.
V
ges
=
n
f
∑
i=1
V
i
+V
R
+V
u
(5.4)
Die individuellen Varianzanteile V
i
der Faktoren sind proportional zum Quadrat
des Effektbetrags. Daraus lässt sich schnell ausrechnen, welchen Varianzanteil ei-
ne reduzierte Bauteiltoleranz produziert. Innerhalb der getesteten Stufenabstände ist
zunächst eine lineare Interpolation zulässig, so liefert die halbierte Bauteiltoleranz
den halben Effektbetrag und ein Viertel der Teilvarianz. Eine Extrapolation muss
immer nachträglich überprüft werden, denn eine Erweiterung der Toleranz kann zu
neuen physikalischen Effekten führen, die im Rahmen der ursprünglichen Versuchs-
reihe nicht aufgetreten sind.
V
i
neu
= V
i
orig
·
∆
2
x
i
neu
∆
2
x
i
orig
(5.5)
Die Quantifizierung des Nutzens erfordert eine Abbildung der Streuungsredukti-
on auf einen monetären Gegenwert. Natürlich ist diese Abbildung sehr produktspe-
zifisch und kann sich mit den Kundenerwartungen auch im Laufe der Zeit ändern.
Offenbar trifft die Parabel als Abbildungsfunktion in vielen Fällen recht gut und
wird üblicherweise angesetzt. Bei allen anderen Funktionen ergibt sich außerdem
ein höherer Berechnungsaufwand. Ausgangspunkt ist eine Negativbetrachtung, also
monetärer Verlust durch Streuung. Ohne Streuung ist der Verlust Null, mit Streu-
ung wächst der Verlust quadratisch an. Die Proportionalitätskonstante erhält man
durch Marktstudien oder Vergleichsmessungen an Konkurrenzprodukten. Wenn die
Bewertung der Toleranz asymmetrisch ist, wird jedem Ast der Parabel eine eigene
Konstante zugewiesen.
Abgesehen von der Kosten-Nutzen-Analyse bringt das Toleranzdesign weitere
Vorteile. Zunächst schließt die Methode mit der Unart ab, pauschal alle Bauteilto-
leranzen zu verringern, was in jedem Fall unnötige Produktionskosten erzeugt. Der
Direktvergleich der positiven Auswirkung ermöglicht eine Rangfolge der notwendi-
gen Veränderungen, auch wenn es sich um völlig unterschiedliche Bauteiltoleranzen
mit jeweils eigenen physikalischen Einheiten handelt.

148 5 Varianten der statistischen Versuchsplanung
.
.
gutes Produkt
schlechtes
Produkt
Abweichung vom Sollwert
Wertverlust
Abb. 5.12 Die grundsätzliche Idee der Kosten-Nutzen Rechnung. Jede Abweichung vom Sollwert
des Qualitätsmerkmales erzeugt einen Wertverlust des Produkts. Gute Produkte liefern hier eine
geringere Streuung. Geht man von einer quadratischen Bewertungskurve aus, ist der Wertverlust
proportional zur Gesamtvarianz des Qualitätsmerkmals. Liegen die Kosten der Abstellmaßnahme
unter dem verursachten Wertverlust, lohnt sich die Maßnahme.
Die Eingangsdaten für Computermodelle unterliegen oft einer erheblichen Unsi-
cherheit. Daraus können Variationen der Ergebnisgrößen erwachsen, die weit über
den eigenlichen Modellfehlern liegen. Kurzum, eine Verfeinerung des Modells wür-
de keinen Sinn machen, bevor die Eingangsdaten in höherer Genauigkeit verfügbar
sind. DOLTSINIS [36] und MARCZYK [105] bringen eindrucksvolle Beispiele dazu.
Toleranzdesign und die im Kapitel Sensitivitätsanalyse vorgestellte Methodik sind
artverwandt. Bei der Sensitivitätsanalyse wird der Bogen weiter gespannt. An die
Stelle von lediglich zwei Einstellungen je Faktor kommen dann sehr große Stich-
proben mit einer repräsentativen Verteilung. Bei nichtlinearen Zusammenhängen
zwischen Faktoreinstellung und Qualitätsmerkmal kommt es in der Regel zu einer
starken Verformung der Verteilungsfunktion. Die stochastische Auswertung liefert
auch in diesen Fällen ein sehr klares Bild von der der zu erwartenden Steuung des
Qualitätsmerkmals.
5.4 Umgang mit kategorialen Faktoren
In der Praxis sind die meisten Faktoren numerischer Natur, also kontinuierlich ein-
stellbar. Das lineare Modell ist auf diesen Faktortyp ausgerichtet, denn es erlaubt
Vorhersagen für Zwischenstufen. Es gibt jedoch auch kategoriale (categorical) Fak-
toren. Diese Faktoren lassen sich nicht zählen, wiegen oder messen. Ihre Einstellung
erfolgt immer in festen Stufen.
Faktor Stufe 1 Stufe 2 Stufe 3
Lieferant Müller Meier Schulze
Verbindungsart schrauben nieten kleben
Verunreinigung Ei Blut Kakao
Musikrichtung Jazz Pop Klassik
Geometrie rund eckig
Verstärkungsblech ohne mit
Tabelle 5.6 Beispiele für kategoriale Fakto-
ren.
5.4 Umgang mit kategorialen Faktoren 149
Wie wertet man diese Faktoren aus? Wie geht man mit Kombinationen aus nu-
merischen und kategorialen Faktoren um? Es gibt mehrere Lösungswege dafür.
Ein Weg besteht darin, den kategorialen Charakter zunächst zu ignorieren und
den Faktor wie einen numerischen Faktor zu behandeln. Insbesondere in der Phase
der Faktorsichtung ist dies völlig unkritisch, denn dann geht es nicht um die Ein-
stellung von mittleren Werten sondern nur um die Identifikation der signifikanten
Faktoren. Ein Mittelwert erscheint zunächst sinnlos, bei näherer Betrachtung lassen
sich aber in vielen Fällen die Eigenschaften kategorialer Faktoren auf einer nume-
rischen Skala beschreiben. Wenn der als numerischer Faktor getarnte kategoriale
Faktor eine große Bedeutung hat, wird die Abbildung auf die entsprechende nume-
rische Eigenschaft erforderlich.
Wenn zum Beispiel die Verbindungsart schrauben besser ist als die Verbindungs-
art kleben, lohnt sich eine genaue Analyse der Unterschiede. Möglicherweise ist das
charakteristische Merkmal die maximale Scherkraft, also letztlich eine numerische
Variable. Geometrien lassen sich in vielen Fällen durch Morphing stufenlos inein-
ander überführen. Clevere Formulierungen mit Shape Variablen machen dann aus
kategorialen Faktoren wieder numerische Faktoren. Ist ein Bauteil mal vorhanden
und mal nicht, kann häufig eine numerische Variable den Sachverhalt elegant be-
schreiben. Die Variable (E-Modul, Blechdicke, etc. ) wird dann so definiert, dass
sie den Wert Null annimmt, wenn das Bauteil nicht vorhanden ist. Die Produkte
verschiedener Lieferanten haben eigene charakteristische Eigenschaften, die sich
normalerweise ebenfalls in Zahlen ausdrücken lassen. Sollte der Faktor Lieferant
eine große Bedeutung haben, ist es ohnehin höchste Zeit, der Sache auf den Grund
zu gehen und die Unterschiede zu analysieren. Wenn der Faktor Musikrichtung zum
Beispiel bei der optimalen Einstellung des MP3-Players eine Rolle spielt, steckt
vermutlich das Zusammenspiel zwischen Frequenzgang und den jeweils wichtigs-
ten Frequenzbändern dahinter. Auch dies sind letztlich numerische Variablen.
Warum dieser Trick? Versuchsplan und Auswertung vereinfachen sich, wenn
man nur mit numerischen Faktoren arbeitet. Dann sind alle Versuchspläne und Be-
schreibungsmodelle einsetzbar. Auch die Optimierung funktioniert dann reibungs-
los im gesamten Faktorraum. Vereinzelte zweistufige kategoriale Faktoren kann
man bei der Optimierung nacheinander auf die beiden Stufen festsetzen und die
Optima vergleichen. Bei dreistufigen kategorialen Faktoren ist diese Taktik nicht
mehr zulässig, weil die Wechselwirkungsterme zwischen den numerischen und den
kategorialen Faktoren des Beschreibungsmodells unsinnig sind.
Sollte die Rückführung auf einen numerischen Faktor nicht möglich sein, sind
einschränkende Randbedingungen zu beachten. Zwischenwerte machen in diesem
Fall keinen Sinn. Man vergleicht lediglich die Ergebnisse der jeweiligen Stufen un-
tereinander. Die Varianzanalyse gibt dann Aufschluss über Effekte und Wechsel-
wirkungen. Als Darstellungen kommen hierbei auch Streudiagramme zum Einsatz,
aufgeteilt nach den Faktorstufen. Die Mischung von numerischen Faktoren und ka-
tegorialen Faktoren ist aufwendig, da man natürlich für die numerischen Faktoren
nach wie vor gerne ein Beschreibungsmodell hätte. Hierzu lassen sich ein belie-
biger Versuchsplan für die numerischen Faktoren mit einem Vollfaktorplan für die
150 5 Varianten der statistischen Versuchsplanung
kategorialen Faktoren multiplikativ verbinden. Für jede Einstellung der kategorialen
Faktoren folgt dann ein eigenes Beschreibungsmodell der numerischen Faktoren.
Die sauberste Lösung ist in jedem Fall der Vollfaktorplan, also ein Versuchsplan
mit allen Kombinationen. Dies ist in der Praxis jedoch nur bei einer geringen Zahl
von Faktoren durchführbar. DoE-Auswerteprogramme bieten allerdings dafür eine
eigene Analyse an, die speziell auf kategoriale Faktoren zugeschnitten ist.
Faktor_A
1
Faktor_B
2
Faktor_C P = 0,0225
1 2
-15 -10 -5 0 5 10 15
Residuen
P = 0,0000
2
P = 0,0000
1
3
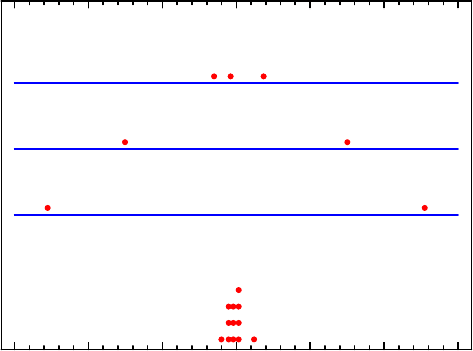
Abb. 5.13 Grafische ANOVA einer Versuchsreihe mit drei kategorialen Faktoren. Die Abbildung
zeigt die Abweichung der jeweiligen Stufenmittelwerte vom Gesamtmittelwert im Vergleich zu
den Residuen. In diesem Beispiel wurden die Faktoren A und B auf zwei Stufen und der Faktor
C auf drei Stufen variiert. Bei allen Faktoren zeigt sich eine signifikante Differenz der jeweili-
gen Stufenmittelwerte im Vergleich zur Varianz der Residuen. Folglich handelt es sich um wahre
Effekte.
Kapitel 6
Computer-Experiment
6.1 Einleitung
Seit KONRAD ZUSE’S Z3 aus dem Jahr 1941, welcher von vielen Wissenschaftlern
als erster funktionstüchtiger Computer angesehen wird, steigen die Rechenleistung
und Speicherkapazität von Computern kontinuierlich an. In den letztem Jahrzehnten
ist der Einsatz von Computersystemen für die Entwicklung technischer Systeme in
vielen Arbeitsbereichen unverzichtbar geworden. Der Einsatzbereich erstreckt sich
dabei von Prüfstandssteuerung, Datenverwaltung und -analyse bis hin zu Simulation
komplexer Systeme. Ziel des Einsatzes von Computersystemen während des Ent-
wicklungsprozesses ist unter anderem die Verbesserung der Produktqualität (zum
Beispiel die Verringerung der Ausfallwahrscheinlichkeit oder Erhöhung der Effizi-
enz). Parallel dazu werden Entwicklungszeiten und -kosten durch den gezielten Ein-
satz von Computersystemen kontinuierlich verringert. Ähnlich zu Versuchsplanun-
gen für physikalische Experimente existieren verschiedenste statistische Methoden,
die einen effizienten Einsatz von Computer-Ressourcen im Entwicklungsprozess
ermöglichen. Eine grundlegende Einführung in das Thema Computer-Experiment
bieten folgende Literaturstellen [156, 157, 92, 11].
6.2 Aufbau und Analyse von Computer-Experimenten
Technische Systeme, die während Entwicklungsprozessen analysiert werden, zeich-
nen sich häufig durch eine Vielzahl von beeinflussenden Faktoren und komple-
xen nicht-linearen Zusammenhängen aus. Simulationsmodelle (im weiteren auch
nur Modelle genannt) dieser Systeme sind dadurch ebenfalls komplex und weisen
meistens lange Rechenzeiten auf. Die Rechenleistung von Computersystemen stei-
gen zwar kontinuierlich an, jedoch entwickeln sich die eingesetzten Modelle eben-
falls weiter, was einerseits zur Erhöhung der Simulationsgüte führt, andererseits die
durchschnittliche Rechenzeit jedoch nicht verringert. Daher ist die effiziente Aus-
K. Siebertz et al., Statistische Versuchsplanung, VDI-Buch, 151
DOI 10.1007/978-3-642-05493-8_6, © Springer-Verlag Berlin Heidelberg 2010
152 6 Computer-Experiment
nutzung der vorhandenen Computer-Ressourcen auch heute noch eine entscheiden-
de Grundvoraussetzung für den sinnvollen Einsatz von Computer-Experimenten.
Die Komplexität der verwendeten Modelle verhindert meist eine direkte analyti-
sche Lösung der betrachteten Aufgabenstellungen (zum Beispiel Leistungsoptimie-
rung eines technischen Systems). Eine Optimierung der betrachteten Systeme mit-
tels des komplexen Simulationsmodells und eines klassischen Optimierungsverfah-
rens wird durch inakzeptable Rechenzeiten ineffektiv. Für den Entwicklungsprozess
werden daher häufig nicht die Originalmodelle sonder Ersatzmodelle (Approxima-
tionsmodelle) verwendet, die das technische System beziehungsweise das komple-
xe Simulationsmodell ausreichend genau beschreiben und gleichzeitig nur minima-
le Computer-Ressourcen erfordern. Ähnlich wie bei physikalischen Experimenten,
kann ein Approximationsmodell aus Experimenten mit dem Simulationsmodell er-
zeugt werden. Es wird dadurch ein vereinfachtes Modell des komplexen Simula-
tionsmodells erstellt, welches lediglich die signifikanten Effekte beinhaltet. Diese
Modelle werden in der Literatur meist als Metamodelle oder Transferfunktionen
bezeichnet [87].
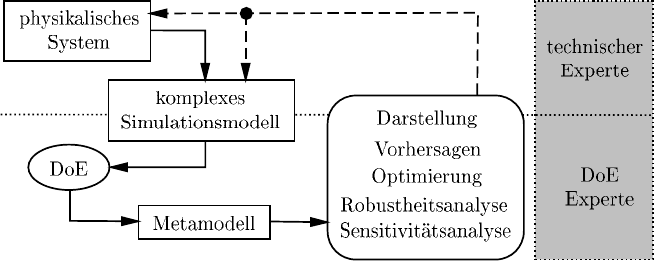
Abbildung 6.1 zeigt schematisch ein typisches Vorgehen bei Computer-Experi-
menten (CE) zur Verbesserung oder Neuentwicklung technischer Systeme.
Abb. 6.1 Computer-Experiment
Im ersten Schritt wird basierend auf physikalischen Zusammenhängen und Er-
fahrungen technischer Experten ein komplexes Simulationsmodell aufgebaut. Mit
Hilfe eines speziell für Computer-Experimente ausgelegtes Versuchsplans (Design
of Experiment) werden Datensätze erzeugt, die es ermöglichen ausreichend genaue
Metamodelle für komplexe und nichtlineare Zusammenhänge zwischen Faktoren
des Modells und der zu analysierenden Ausgangsgrößen zu ermitteln. Mit diesen
Metamodellen können anschließend verschiedenste Analysen effizient durchgeführt
werden. Die Analysen variieren dabei von einfachen grafischen Darstellungen ge-
suchter Zusammenhängen zwischen Faktoren und Ausgangsgrößen des Systems,
über Sensitivitätsanalysen der verschiedenen Faktoren bis hin zu Optimierungen
mit Berücksichtigung der Robustheit gegenüber Störgrößen. Die Ergebnisse und
Schlussfolgerungen dieser Analysen fließen anschließend in die Verbesserung des

6.2 Aufbau und Analyse von Computer-Experimenten 153
technischen Systems ein und wenn notwendig in das dazugehörige komplexe Simu-
lationsmodell. Hierbei handelt es sich meist um einen iterativen Prozess, wobei die
Anzahl der notwendigen Iterationen durch den gezielten Einsatz von Versuchsplä-
nen (DoE) und Algorithmen zur Erstellung von Metamodellen minimiert wird.
6.2.1 Vergleich von Computer- und physikalischem Experiment
Der Einsatz von Versuchsplänen, die in den letzten Jahrzehnten speziell für physika-
lische Experimente entwickelt wurden, wie zum Beispiel Teilfaktorpläne oder Cen-
tral Composite Design, sind zwar grundsätzlich auch für Computer-Experimente
(CE) verwendbar, jedoch können Sie nicht von speziellen Eigenschaften der Com-
puter-Experimente profitieren. Der direkte Vergleich zwischen Computer- und phy-
sikalischen Experimenten zeigt einige grundsätzlich unterschiedliche Eigenschaften
welche in Tabelle 6.1 aufgelistet sind.
Computer Physikalisch
deterministisch stochastisch
keine Messfehler Messfehler
hohe Faktoranzahl geringe Faktoranzahl
flexible Stufenwahl eingeschränkte Stufenwahl
einfache Änderung von Faktoren Änderung von Faktoren oft schwierig
oder zeitaufwendig
Tabelle 6.1 Vergleich von Computer- und physikalisches Experiment
Ein System beziehungsweise Modell wird als deterministisch bezeichnet, wenn
eine eindeutige Beziehung zwischen Eingangsdaten (Faktoren) und Ausgangsdaten
(Gütekriterien) vorliegt. Gleiche Eingangsdaten liefern immer identische Ausgangs-
daten. Liefert ein System hingegen für gleiche Eingangsdaten unterschiedliche Aus-
gangsdaten (zum Beispiel durch Messstreuung), wird das System als stochastisch
bezeichnet. Simulationsmodelle sind deterministisch, so dass Wiederholungsmes-
sungen beziehungsweise -simulationen mit identischen Faktoren, wie sie in phy-
sikalischen Experimenten zur Dämpfung der Versuchsstreuung notwendig sind, in
Computer-Experimenten unnötig sind.
Tendenziell ist festzustellen, dass in Computer-Experimenten mehr Faktoren
in den Untersuchungen berücksichtigt werden als in physikalischen Experimen-
ten. Dieses basiert unter anderem darauf, dass Faktoren in Simulationsmodellen
leichter zu verändern oder kontrollieren sind als in physikalischen Versuchsaufbau-
ten. Die Umgebungstemperatur oder Eigenschaften einer eingesetzten Flüssigkeit
großer technischer Systeme können im physikalischen Experiment nicht verändert
werden, was in einem Simulationsmodel jedoch meist keine Schwierigkeit darstellt.
Zusätzlich sind physikalische Experimente auf vorhandene oder kurzfristig liefer-
bare Bauteile beschränkt. Durchmesser von Rohrleitungen können beispielsweise
154 6 Computer-Experiment
kurzfristig nur in Standardmaße geliefert werden, was gerade bei engen Zeitfens-
tern in der Entwicklung neuer Produkte die Spielräume in den Versuchsplänen stark
einschränkt. Diese Einschränkungen treten bei Verwendung von Simulationsmodel-
len nicht auf.
Ein weiterer wichtiger Punkt im Vergleich zwischen Computer- und physikali-
schem Experiment ist die Veränderung von Faktoreinstellungen (Faktorstufen). Die
Änderung eines Faktors in einem physikalischen Experiment erfordert meist einen
Umbau der Prüfeinrichtung. Als Beispiel sei hier die Änderung eines Rohrdurch-
messers genannt, welcher den Wechsel der zu verändernden Rohrleitung bedingt.
Zur Minimierung des Versuchsaufwands in physikalischen Experimenten kommt
daher der genauen und geschickten Versuchsplanung (zum Beispiel Versuchsrei-
henfolge) eine hohe Bedeutung zu. Bei der Versuchsreihenfolge im physikalischem
Experiment sind jedoch zusätzlich zeitliche Veränderungen des Systems (Drift) zu
berücksichtigen, so dass Faktorvariationen randomisiert erfolgen sollten. Beim Ein-
satz von Simulationsmodellen sind Überlegungen zur Versuchsreihenfolge von nur
geringer Relevanz, da Faktoren leicht zu ändern sind und die zeitliche Reihenfolge
der Simulation keinen Einfluss auf das Simulationsergebnis hat.
6.2.2 Testfelder für Computer-Experimente
Die im Kapitel 6.2.1 aufgeführten Eigenschaften von Computer-Experimenten er-
möglichen es spezielle Testfelder einzusetzen, welche Simulationsmodelle ideal
ausnutzen und eine maximale Informationsmenge aus einer vorgegebenen Anzahl
an Versuchen liefern. Abbildung 6.2a zeigt einen klassischen Vollfaktorplan mit
zwei Faktoren und 9 Versuchsläufen. Da nur die Stufen −1,0,1 besetzt sind er-
geben sich relativ große Bereiche im Inneren des Faktorraums, die keine Testpunk-
te enthalten wodurch keine Informationen für diese Bereiche vorliegen. Weiterhin
können Pseudo Wiederholungen auftreten, die nicht zur Erhöhung der Informati-
onsmenge beitragen. Betrachtet wird dazu der Fall, dass Faktor 2 keinen oder einen
vernachlässigbaren Einfluss auf die Ausgangsvariable des betrachteten Sytem auf-
weist
z.B. y (x) = x
3
1
. Jeweils drei Testpunkte mit gleicher Faktorstufe für Faktor
x
1
liefern das gleiche Ergebnis für y. Die drei Testpunkte ergeben bei vereinfachter
Betrachtung für den Haupteffekt von x
1
auf y genauso viele Informationen wie ein
einzelner Testpunkt. Es wurden somit zwei pseudo Wiederholungen durchgeführt,
die trotz erhöhtem Testaufwand keine zusätzlichen Informationen für die Analyse
des Zusammenhangs zwischen x
1
und y liefern. Zu beachten ist, dass keine Ver-
suchsstreuung durch Mittelwertbildung gedämpft werden muss.
Abbildung
6.2b zeigt im Vergleich ein Latin Hypercube Testplan (Kapitel 7.3.3)
welcher bei 2 Faktoren und 9 Testläufen einem rotierten Vollfaktorplan ähnelt.
Im Gegensatz zum Vollfaktorplan wird hier jeder Faktor auf 9 äquidistante Stu-
fen (gleich der Anzahl an Testpunkten) getestet, die jeweils nur einmal verwendet
werden. Die Orthogonalität der Faktoren ist in diesem Beispiel weiterhin gegeben,
so dass die Haupteffekte sauber getrennt werden können. Die Testpunkte sind dabei
