Stewart J. Calculus

Подождите немного. Документ загружается.

852

VECTOR

FUNCTIONS

The functions that we have been using so far have been real-valued functions. We now

study functions whose values are vectors because such functions are needed to describe

curves and surfaces in space. We will also use vector-valued functions to describe the

motion of objects through space. In particular, we will use them to derive Kepler’s laws

of planetary motion.

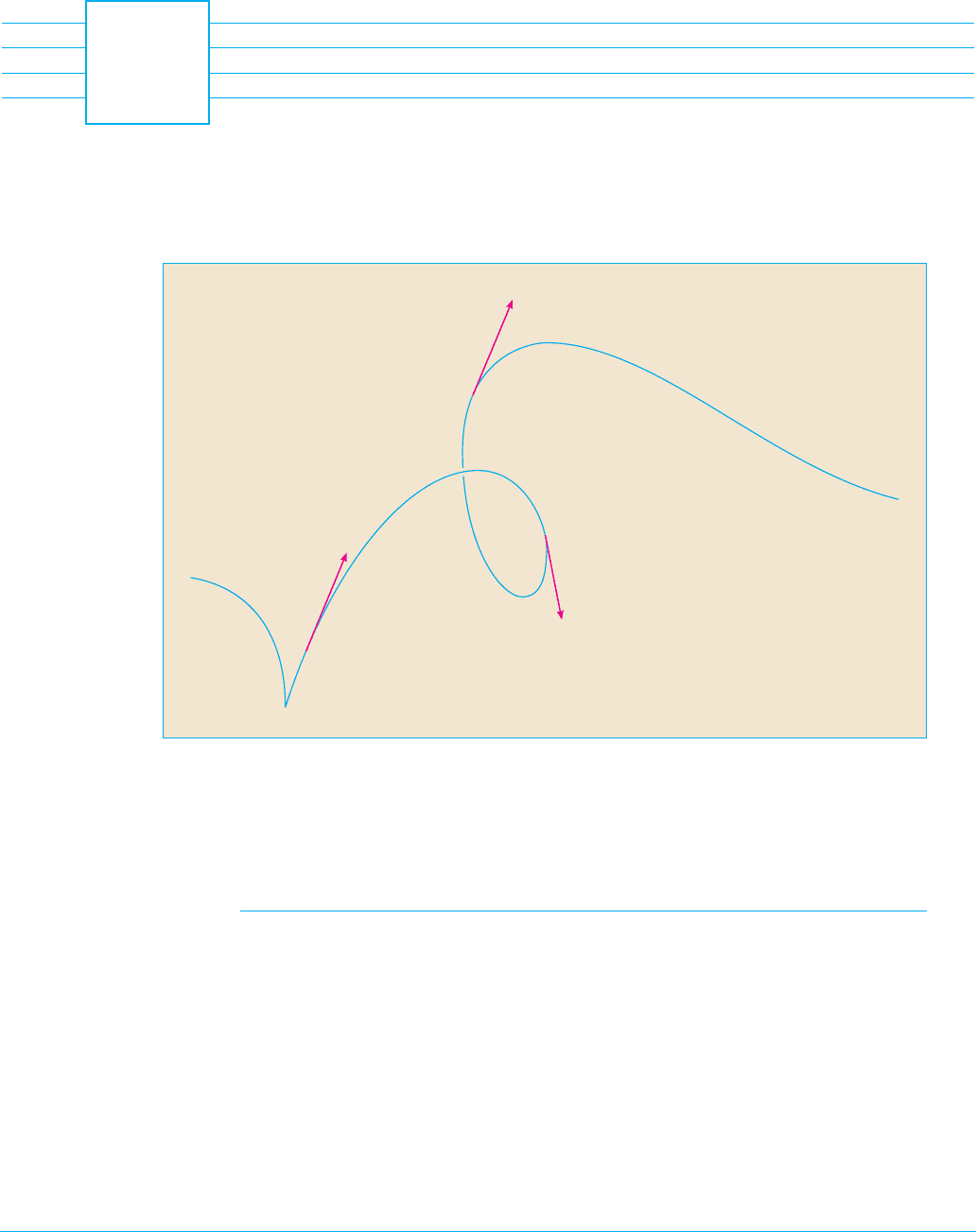
Tangent vectors show the direction in

which a space curve proceeds at any point.

VECTOR FUNCTIONS AND SPACE CURVES

In general, a function is a rule that assigns to each element in the domain an element in the

range. A vector-valued function, or vector function, is simply a function whose domain

is a set of real numbers and whose range is a set of vectors. We are most interested in vec-

tor functions whose values are three-dimensional vectors. This means that for every num-

ber in the domain of there is a unique vector in denoted by . If , , and

are the components of the vector , then , , and are real-valued functions called the

component functions of and we can write

We usually use the letter to denote the independent variable because it represents time in

most applications of vector functions.

EXAMPLE 1 If

then the component functions are

By our usual convention, the domain of consists of all values of for which the expres-

sion for is deﬁned. The expressions , , and are all deﬁned when

and . Therefore the domain of is the interval . M

The limit of a vector function is deﬁned by taking the limits of its component func-

tions as follows.

If , then

provided the limits of the component functions exist.

Equivalently, we could have used an deﬁnition (see Exercise 45). Limits of vector

functions obey the same rules as limits of real-valued functions (see Exercise 43).

EXAMPLE 2 Find , where .

SOLUTION According to Deﬁnition 1, the limit of r is the vector whose components are the

limits of the component functions of r:

(by Equation 3.4.2) M苷 i ⫹ k

lim

r共t兲苷

关

lim

共1 ⫹ t

兲

兴

i ⫹

关

lim

⫺t

兴

j ⫹

冋

lim

sin t

册

r共t兲苷共1 ⫹ t

兲

i ⫹ te

⫺t

j ⫹

sin t

klim

t l 0

r共t兲

␧-

␦

lim

t l a

r共t兲苷

具

lim

t l a

f 共t兲, lim

t l a

t共t兲, lim

t l a

h共t兲

典

r共t兲苷具 f 共t兲, t共t兲, h共t兲典

关0, 3兲rt 艌 03 ⫺ t ⬎ 0

ln共3 ⫺ t兲t

r共t兲

h共t兲苷

t共t兲苷 ln共3 ⫺ t兲f 共t兲苷 t

r共t兲苷

具

, ln共3 ⫺ t兲,

典

r共t兲苷具 f 共t兲, t共t兲, h共t兲典苷 f 共t兲

i ⫹ t共t兲

j ⫹ h共t兲

htfr共t兲

h共t兲t共t兲f 共t兲r共t兲V

14.1

853

N If , this deﬁnition is equiva-

lent to saying that the length and direction of the

vector approach the length and direction of

the vector .L

r共t兲

lim

t la

r共t兲苷 L

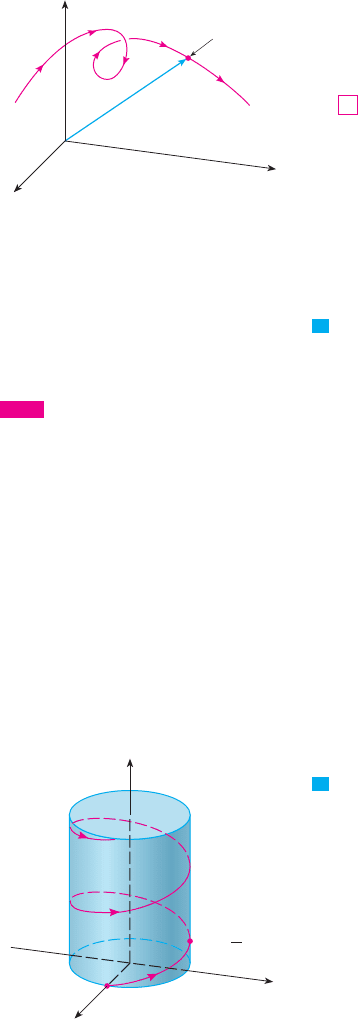
A vector function is continuous at a if

In view of Deﬁnition 1, we see that is continuous at if and only if its component func-

tions , , and are continuous at .

There is a close connection between continuous vector functions and space curves.

Suppose that , , and are continuous real-valued functions on an interval . Then the set

of all points in space, where

and varies throughout the interval , is called a space curve. The equations in (2) are

called parametric equations of C and is called a parameter. We can think of as being

traced out by a moving particle whose position at time is . If we now con-

sider the vector function , then is the position vector of the

point on . Thus any continuous vector function deﬁnes a space curve

that is traced out by the tip of the moving vector , as shown in Figure 1.

EXAMPLE 3 Describe the curve deﬁned by the vector function

SOLUTION The corresponding parametric equations are

which we recognize from Equations 13.5.2 as parametric equations of a line passing

through the point and parallel to the vector . Alternatively, we could

observe that the function can be written as , where and

, and this is the vector equation of a line as given by Equation 13.5.1. M

Plane curves can also be represented in vector notation. For instance, the curve given

by the parametric equations and (see Example 1 in Section 11.1)

could also be described by the vector equation

where and .

EXAMPLE 4 Sketch the curve whose vector equation is

SOLUTION The parametric equations for this curve are

Since , the curve must lie on the circular cylinder

. The point lies directly above the point , which moves

counterclockwise around the circle in the xy-plane. (See Example 2 in

Section 11.1.) Since , the curve spirals upward around the cylinder as increases.

The curve, shown in Figure 2, is called a helix. M

tz 苷 t

⫹ y

苷 1

共x, y, 0兲共x, y, z兲x

⫹ y

苷 1

⫹ y

苷 cos

t ⫹ sin

t 苷 1

z 苷 ty 苷 sin tx 苷 cos t

r共t兲苷 cos t i ⫹ sin t j ⫹ t k

j 苷具0, 1典i 苷具1, 0典

r共t兲苷具t

⫺ 2t, t ⫹ 1典苷共t

⫺ 2t兲

i ⫹ 共t ⫹ 1兲

y 苷 t ⫹ 1x 苷 t

⫺ 2t

v 苷具1, 5, 6典

苷具1, 2, ⫺1典r 苷 r

⫹ tv

具1, 5, 6典共1, 2, ⫺1兲

z 苷 ⫺1 ⫹ 6ty 苷 2 ⫹ 5tx 苷 1 ⫹ t

r共t兲苷具1 ⫹ t, 2 ⫹ 5t, ⫺1 ⫹ 6t典

r共t兲C

rCP

(

f 共t兲, t共t兲, h共t兲

)

r共t兲r共t兲苷具 f 共t兲, t共t兲, h共t兲典

(

f 共t兲, t共t兲, h共t兲

)

z 苷 h共t兲y 苷 t共t兲x 苷 f 共t兲

共x, y, z兲C

Ihtf

ahtf

lim

t l a

r共t兲苷 r共a兲

854

||||

CHAPTER 14 VECTOR FUNCTIONS

FIGURE 1

C is traced out by the tip of a moving

position vector r(t).

{

f(t), g(t), h(t)

}

r(t)=kf(t), g(t), h(t)

Visual 14.1A shows several curves

being traced out by position vectors,

including those in Figures 1 and 2.

TEC

FIGURE 2



”0,1, ’

(1,0,0)

The corkscrew shape of the helix in Example 4 is familiar from its occurrence in coiled

springs. It also occurs in the model of DNA (deoxyribonucleic acid, the genetic material

of living cells). In 1953 James Watson and Francis Crick showed that the structure of the

DNA molecule is that of two linked, parallel helixes that are intertwined as in Figure 3.

In Examples 3 and 4 we were given vector equations of curves and asked for a geo-

metric description or sketch. In the next two examples we are given a geometric descrip-

tion of a curve and are asked to ﬁnd parametric equations for the curve.

EXAMPLE 5 Find a vector equation and parametric equations for the line segment that

joins the point to the point .

SOLUTION In Section 13.5 we found a vector equation for the line segment that joins the tip

of the vector to the tip of the vector :

(See Equation 13.5.4.) Here we take and to obtain a

vector equation of the line segment from to :

The corresponding parametric equations are

EXAMPLE 6 Find a vector function that represents the curve of intersection of the

cylinder and the plane .

SOLUTION Figure 5 shows how the plane and the cylinder intersect, and Figure 6 shows the

curve of intersection C, which is an ellipse.

FIGURE 5 FIGURE 6

(0,_1,3)

(1,0,2)

(_1,0,2)

(0,1,1)

y+z=2

≈+¥=1

y ⫹ z 苷 2x

⫹ y

苷 1

0 艋 t 艋 1z 苷 ⫺2 ⫹ 5ty 苷 3 ⫺ 4tx 苷 1 ⫹ t

0 艋 t 艋 1r共t兲苷具1 ⫹ t, 3 ⫺ 4t, ⫺2 ⫹ 5t 典

0 艋 t 艋 1r共t兲苷共1 ⫺ t兲具1, 3, ⫺2典 ⫹ t具2, ⫺1, 3典

苷具2, ⫺1, 3典r

苷具1, 3, ⫺2典

0 艋 t 艋 1r共t兲苷共1 ⫺ t兲r

⫹ tr

Q共2, ⫺1, 3兲P共1, 3, ⫺2兲

SECTION 14.1 VECTOR FUNCTIONS AND SPACE CURVES

||||

855

FIGURE 3

N Figure 4 shows the line segment in

Example 5.

FIGURE 4

Q(2,_1,3)

P(1,3,_2)

The projection of C onto the xy-plane is the circle . So we know

from Example 2 in Section 11.1 that we can write

From the equation of the plane, we have

So we can write parametric equations for C as

The corresponding vector equation is

This equation is called a parametrization of the curve C. The arrows in Figure 6 indicate

the direction in which C is traced as the parameter t increases.

USING COMPUTERS TO DRAW SPACE CURVES

Space curves are inherently more difﬁcult to draw by hand than plane curves; for an accu-

rate representation we need to use technology. For instance, Figure 7 shows a computer-

generated graph of the curve with parametric equations

It’s called a toroidal spiral because it lies on a torus. Another interesting curve, the tre-

foil knot, with equations

is graphed in Figure 8. It wouldn’t be easy to plot either of these curves by hand.

Even when a computer is used to draw a space curve, optical illusions make it difﬁcult

to get a good impression of what the curve really looks like. (This is especially true in

Figure 8. See Exercise 44.) The next example shows how to cope with this problem.

EXAMPLE 7 Use a computer to draw the curve with vector equation

This curve is called a twisted cubic.

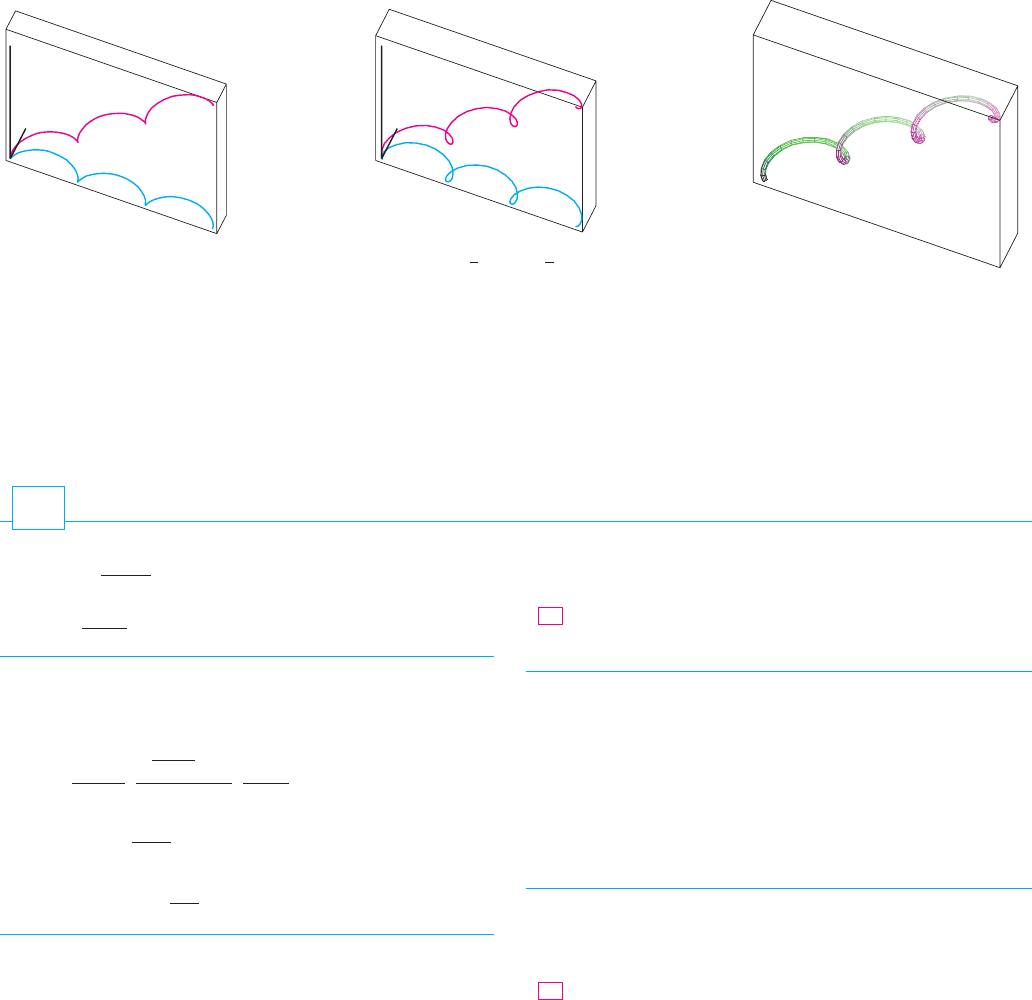
SOLUTION We start by using the computer to plot the curve with parametric equations

, , for . The result is shown in Figure 9(a), but it’s hard to

see the true nature of the curve from that graph alone. Most three-dimensional computer

graphing programs allow the user to enclose a curve or surface in a box instead of dis-

playing the coordinate axes. When we look at the same curve in a box in Figure 9(b), we

have a much clearer picture of the curve. We can see that it climbs from a lower corner

of the box to the upper corner nearest us, and it twists as it climbs.

⫺2 艋 t 艋 2z 苷 t

y 苷 t

x 苷 t

r共t兲苷具t, t

, t

典.

z 苷 sin 1.5ty 苷共2 ⫹ cos 1.5t兲 sin tx 苷共2 ⫹ cos 1.5t兲 cos t

z 苷 cos 20ty 苷共4 ⫹ sin 20t兲 sin tx 苷共4 ⫹ sin 20t兲 cos t

0 艋 t 艋 2

␲

r共t兲苷 cos t i ⫹ sin t j ⫹ 共2 ⫺ sin t兲

0 艋 t 艋 2

␲

z 苷 2 ⫺ sin ty 苷 sin tx 苷 cos t

z 苷 2 ⫺ y 苷 2 ⫺ sin t

0 艋 t 艋 2

␲

y 苷 sin tx 苷 cos t

⫹ y

苷 1, z 苷 0

856

||||

CHAPTER 14 VECTOR FUNCTIONS

FIGURE 7 A toroidal spiral

FIGURE 8 A trefoil knot

We get an even better idea of the curve when we view it from different vantage

points. Part (c) shows the result of rotating the box to give another viewpoint. Parts (d),

(e), and (f) show the views we get when we look directly at a face of the box. In par-

ticular, part (d) shows the view from directly above the box. It is the projection of the

curve on the -plane, namely, the parabola . Part (e) shows the projection on

the -plane, the cubic curve . It’s now obvious why the given curve is called a

twisted cubic. M

Another method of visualizing a space curve is to draw it on a surface. For instance, the

twisted cubic in Example 7 lies on the parabolic cylinder . (Eliminate the parame-

ter from the ﬁrst two parametric equations, and .) Figure 10 shows both the

cylinder and the twisted cubic, and we see that the curve moves upward from the origin

along the surface of the cylinder. We also used this method in Example 4 to visualize the

helix lying on the circular cylinder (see Figure 2).

A third method for visualizing the twisted cubic is to realize that it also lies on the cylin-

der . So it can be viewed as the curve of intersection of the cylinders and

. (See Figure 11.)

FIGURE 11

z 苷 x

y 苷 x

z 苷 x

y 苷 t

x 苷 t

y 苷 x

z 苷 x

y 苷 x

01234

210_1_2

01234

(a) (b) (c)

(e)(d) (f)

FIGURE 9

Views of the twisted cubic

SECTION 14.1 VECTOR FUNCTIONS AND SPACE CURVES

||||

857

In Visual 14.1B you can rotate the

box in Figure 9 to see the curve from any

viewpoint.

TEC

FIGURE 10

Visual 14.1C shows how curves

arise as intersections of surfaces.

TEC

We have seen that an interesting space curve, the helix, occurs in the model of DNA.

Another notable example of a space curve in science is the trajectory of a positively

charged particle in orthogonally oriented electric and magnetic ﬁelds E and B. Depending

on the initial velocity given the particle at the origin, the path of the particle is either a

space curve whose projection on the horizontal plane is the cycloid we studied in Section

11.1 [Figure 12(a)] or a curve whose projection is the trochoid investigated in Exercise 40

in Section 11.1 [Figure 12(b)].

For further details concerning the physics involved and animations of the trajectories of

the particles, see the following websites:

www.phy.ntnu.edu.tw/java/emField/emField.html

www.physics.ucla.edu/plasma-exp/Beam/

(a)r(t) = kt-sint, 1-cost, tl

(b)r(t) =

t- sint, 1- cost, t

858

||||

CHAPTER 14 VECTOR FUNCTIONS

N Some computer algebra systems provide us

with a clearer picture of a space curve by enclos-

ing it in a tube. Such a plot enables us to see

whether one part of a curve passes in front of or

behind another part of the curve. For example,

Figure 13 shows the curve of Figure 12(b) as ren-

dered by the tubeplot command in Maple.

9. 10.

11. 12.

14.

15–18 Find a vector equation and parametric equations for the line

segment that joins to .

15. ,

16. ,

17. ,

18. ,

19–24 Match the parametric equations with the graphs

(labeled I–VI). Give reasons for your choices.

20. ,,z 苷 e

⫺t

y 苷 t

x 苷 t

z 苷 sin 4ty 苷 tx 苷 cos 4t

19.

Q共6, ⫺1, 2兲P共⫺2, 4, 0兲

Q共4, 1, 7兲P共1, ⫺1, 2兲

Q共2, 3, 1兲P共1, 0, 1兲

Q共1, 2, 3兲P共0, 0, 0兲

r共t兲苷 cos t i ⫺ cos t j ⫹ sin t k

r共t兲苷 t

i ⫹ t

j ⫹ t

13.

r共t兲苷 t

i ⫹ t j ⫹ 2kr共t兲苷具1, cos t, 2 sin t典

r共t兲苷具1 ⫹ t, 3t, ⫺t 典r共t兲苷具t, cos 2t, sin 2t典

1–2 Find the domain of the vector function.

3–6 Find the limit.

7–14 Sketch the curve with the given vector equation. Indicate

with an arrow the direction in which increases.

7. 8. r共t兲苷具t

, t

典r共t兲苷具sin t, t典

lim

⬁

冓

arctan t, e

⫺2t

ln t

冔

lim

冉

⫺3t

i ⫹

sin

j ⫹ cos 2t k

冊

lim

冓

⫺ 1

1 ⫹ t

⫺ 1

1 ⫹ t

冔

lim

⫹

具cos t, sin t, t ln t 典

r共t兲苷

t ⫺ 2

t ⫹ 2

i ⫹ sin t j ⫹ ln共9 ⫺ t

兲 k

r共t兲苷

具

4 ⫺ t

, e

⫺3t

, ln共t ⫹ 1兲

典

EXERCISES

14.1

FIGURE 12

Motion of a charged particle in

orthogonally oriented electric

and magnetic fields

FIGURE 13

;

33.

Graph the curve with parametric equations

, ,

. Explain the appearance of the graph by

showing that it lies on a cone.

;

34.

Graph the curve with parametric equations

Explain the appearance of the graph by showing that it lies on

a sphere.

35.

Show that the curve with parametric equations ,

, passes through the points (1, 4, 0)

and (9, ⫺8, 28) but not through the point (4, 7, ⫺6).

36–38

Find a vector function that represents the curve of

intersection of the two surfaces.

36.

The cylinder and the surface

The cone and the plane

38.

The paraboloid and the parabolic

cylinder

;

Try to sketch by hand the curve of intersection of the circular

cylinder and the parabolic cylinder .

Then ﬁnd parametric equations for this curve and use these

equations and a computer to graph the curve.

;

40.

Try to sketch by hand the curve of intersection of the

parabolic cylinder and the top half of the ellipsoid

. Then ﬁnd parametric equations for

this curve and use these equations and a computer to graph

the curve.

41.

If two objects travel through space along two different curves,

it’s often important to know whether they will collide. (Will a

missile hit its moving target? Will two aircraft collide?) The

curves might intersect, but we need to know whether the

objects are in the same position at the same time. Suppose the

trajectories of two particles are given by the vector functions

for . Do the particles collide?

42.

Two particles travel along the space curves

Do the particles collide? Do their paths intersect?

43.

Suppose and are vector functions that possess limits as

and let be a constant. Prove the following properties

of limits.

(a) lim

关u共t兲 ⫹ v共t兲兴苷 lim

u共t兲 ⫹ lim

v共t兲

ct l a

共t兲苷具1 ⫹ 2t, 1 ⫹ 6t, 1 ⫹ 14t 典r

共t兲苷具t, t

, t

典

t 艌 0

共t兲苷具4t ⫺ 3, t

, 5t ⫺ 6典r

共t兲苷具t

, 7t ⫺ 12, t

典

⫹ 4y

⫹ 4z

苷 16

y 苷 x

z 苷 x

⫹ y

苷 4

39.

y 苷 x

z 苷 4x

⫹ y

z 苷 1 ⫹ y

z 苷

⫹ y

37.

z 苷 xyx

⫹ y

苷 4

z 苷 1 ⫹ t

y 苷 1 ⫺ 3t

x 苷 t

z 苷 0.5 cos 10t

y 苷

1 ⫺ 0.25 cos

10t

sin t

x 苷

1 ⫺ 0.25 cos

10t

cos t

z 苷 1 ⫹ cos 16t

y 苷共1 ⫹ cos 16t兲 sin tx 苷共1 ⫹ cos 16t兲 cos t

22.

23.

24.

Show that the curve with parametric equations ,

, lies on the cone , and use this

fact to help sketch the curve.

26.

Show that the curve with parametric equations ,

, is the curve of intersection of the

surfaces and . Use this fact to help sketch

the curve.

27.

At what points does the curve inter-

sect the paraboloid ?

28.

At what points does the helix intersect

the sphere ?

;

29–32

Use a computer to graph the curve with the given vector

equation. Make sure you choose a parameter domain and view-

points that reveal the true nature of the curve.

29.

30.

31.

32.

r共t兲苷具t, e

, cos t典

r共t兲苷具t, t sin t, t cos t典

r共t兲苷具t

, ln t, t典

r共t兲苷具cos t sin 2t, sin t sin 2t, cos 2t 典

⫹ y

⫹ z

苷 5

r共t兲苷具sin t, cos t, t典

z 苷 x

⫹ y

r共t兲苷 t i ⫹ 共2t ⫺ t

兲 k

⫹ y

苷 1z 苷 x

z 苷 sin

ty 苷 cos t

x 苷 sin t

苷 x

⫹ y

z 苷 ty 苷 t sin t

x 苷 t cos t

25.

III IV

III

VVI

z 苷 ln ty 苷 sin tx 苷 cos t

z 苷 sin 5ty 苷 sin tx 苷 cos t

z 苷 e

⫺t

y 苷 e

⫺t

sin 10tx 苷 e

⫺t

cos 10t

z 苷 t

y 苷 1兾共1 ⫹ t

兲x 苷 t

21.

CHAPTER 14 VECTOR FUNCTIONS AND SPACE CURVES

||||

859

Openmirrors.com

that the projection of the curve onto the -plane has polar

coordinates and , so varies between 1

and 3. Then show that has maximum and minimum values

when the projection is halfway between and .

;

When you have ﬁnished your sketch, use a computer to draw

the curve with viewpoint directly above and compare with your

sketch. Then use the computer to draw the curve from several

other viewpoints. You can get a better impression of the curve

if you plot a tube with radius 0.2 around the curve. (Use the

tubeplot command in Maple.)

45. Show that if and only if for every

there is a number such that

if then

ⱍ

r共t兲 ⫺ b

ⱍ

⬍

␧0

⬍

ⱍ

t ⫺ a

ⱍ

⬍

␦

⬎ 0

␧⬎0lim

t l a

r共t兲苷 b

r 苷 3r 苷 1

␪

苷 tr 苷 2 ⫹ cos 1.5t

(b)

(c)

(d)

44. The view of the trefoil knot shown in Figure 8 is accurate, but

it doesn’t reveal the whole story. Use the parametric equations

to sketch the curve by hand as viewed from above, with gaps

indicating where the curve passes over itself. Start by showing

z 苷 sin 1.5t

y 苷共2 ⫹ cos 1.5t兲 sin t

x 苷共2 ⫹ cos 1.5t兲 cos t

lim

关u共t兲 ⫻ v共t兲兴苷 lim

u共t兲 ⫻ lim

v共t兲

lim

关u共t兲 ⴢ v共t兲兴苷 lim

u共t兲 ⴢ lim

v共t兲

lim

cu共t兲苷 c lim

u共t兲

860

||||

CHAPTER 14 VECTOR FUNCTIONS

DERIVATIVES AND INTEGRALS OF VECTOR FUNCTIONS

Later in this chapter we are going to use vector functions to describe the motion of plan-

ets and other objects through space. Here we prepare the way by developing the calculus

of vector functions.

DERIVATIVES

The derivative of a vector function is deﬁned in much the same way as for real-

valued functions:

if this limit exists. The geometric signiﬁcance of this deﬁnition is shown in Figure 1. If the

points and have position vectors and , then PQ

represents the vector

, which can therefore be regarded as a secant vector. If , the scalar

multiple has the same direction as . As , it

appears that this vector approaches a vector that lies on the tangent line. For this reason,

the vector is called the tangent vector to the curve deﬁned by at the point , pro-

vided that exists and . The tangent line to at is deﬁned to be the line

through parallel to the tangent vector . We will also have occasion to consider the

unit tangent vector, which is

The following theorem gives us a convenient method for computing the derivative of a

vector function : just differentiate each component of .

THEOREM If , where , , and

are differentiable functions, then

r⬘共t兲苷具 f ⬘共t兲, t⬘共t兲, h⬘共t兲典苷 f ⬘共t兲

i ⫹ t⬘共t兲

j ⫹ h⬘共t兲

tfr共t兲苷具 f 共t兲, t共t兲, h共t兲典苷 f 共t兲

i ⫹ t共t兲

j ⫹ h共t兲

T共t兲苷

r⬘共t兲

ⱍ

r⬘共t兲

ⱍ

r⬘共t兲P

PCr⬘共t兲苷 0r⬘共t兲

Prr⬘共t兲

h l 0r共t ⫹ h兲 ⫺ r共t兲共1兾h兲共r共t ⫹ h兲 ⫺ r共t兲兲

h ⬎ 0r共t ⫹ h兲 ⫺ r共t兲

r共t ⫹ h兲r共t兲QP

苷 r⬘共t兲苷 lim

h l 0

r共t ⫹ h兲 ⫺ r共t兲

rr⬘

14.2

(b) The tangent vector

(a) The secant vector

r(t+h)-r(t)

r(t)

r(t+h)

r(t+h)-r(t)

r(t+h)

r(t)

rª(t)

FIGURE 1

Visual 14.2 shows an animation of

Figure 1.

TEC

PROOF

EXAMPLE 1

(a) Find the derivative of .

(b) Find the unit tangent vector at the point where .

SOLUTION

(a) According to Theorem 2, we differentiate each component of r:

(b) Since and , the unit tangent vector at the point is

EXAMPLE 2 For the curve , ﬁnd and sketch the position

vector and the tangent vector .

SOLUTION We have

The curve is a plane curve and elimination of the parameter from the equations ,

gives , . In Figure 2 we draw the position vector

starting at the origin and the tangent vector starting at the corresponding point .

EXAMPLE 3 Find parametric equations for the tangent line to the helix with para-

metric equations

at the point .

SOLUTION The vector equation of the helix is , so

r⬘共t兲苷具⫺2 sin t, cos t, 1典

r共t兲苷具2 cos t, sin t, t 典

共0, 1,

␲

兾2兲

z 苷 ty 苷 sin tx 苷 2 cos t

共1, 1兲r⬘共1兲

r共1兲苷 i ⫹ jx 艌 0y 苷 2 ⫺ x

y 苷 2 ⫺ t

x 苷

r⬘共1兲苷

i ⫺ jandr⬘共t兲苷

i ⫺ j

r⬘共1兲r共1兲

r⬘共t兲r共t兲苷

i ⫹ 共2 ⫺ t兲

T共0兲苷

r⬘共0兲

ⱍ

r⬘共0兲

ⱍ

苷

j ⫹ 2k

1 ⫹ 4

苷

j ⫹

共1, 0, 0兲r⬘共0兲苷 j ⫹ 2kr共0兲苷 i

r⬘共t兲苷 3t

i ⫹ 共1 ⫺ t兲e

⫺t

j ⫹ 2 cos 2t k

t 苷 0

r共t兲苷共1 ⫹ t

兲

i ⫹ te

⫺t

j ⫹ sin 2t k

苷具 f ⬘共t兲, t⬘共t兲, h⬘共t兲典

苷

冓

lim

⌬t l 0

f 共t ⫹⌬t兲 ⫺ f 共t兲

⌬t

, lim

⌬t l 0

t共t ⫹⌬t兲 ⫺ t共t兲

⌬t

, lim

⌬t l 0

h共t ⫹⌬t兲 ⫺ h共t兲

⌬t

冔

苷 lim

⌬t l 0

冓

f 共t ⫹⌬t兲 ⫺ f 共t兲

⌬t

t共t ⫹⌬t兲 ⫺ t共t兲

⌬t

h共t ⫹⌬t兲 ⫺ h共t兲

⌬t

冔

苷 lim

⌬t l 0

⌬t

关具f 共t ⫹⌬t兲, t共t ⫹⌬t兲, h共t ⫹⌬t兲典 ⫺ 具 f 共t兲, t共t兲, h共t兲典兴

r⬘共t兲苷 lim

⌬t l 0

⌬t

关r共t ⫹⌬t兲 ⫺ r共t兲兴

SECTION 14.2 DERIVATIVES AND INTEGRALS OF VECTOR FUNCTIONS

||||

861

r(1)

rª(1)

(1,1)

FIGURE 2