Stewart J. Calculus
Подождите немного. Документ загружается.

The parameter value corresponding to the point is , so the tangent
vector there is . The tangent line is the line through
parallel to the vector , so by Equations 13.5.2 its parametric equations are
M
Just as for real-valued functions, the second derivative of a vector function r is the
derivative of , that is, . For instance, the second derivative of the function in
Example 3 is
DIFFERENTIATION RULES
The next theorem shows that the differentiation formulas for real-valued functions have
their counterparts for vector-valued functions.
THEOREM Suppose and are differentiable vector functions, is a scalar,
and is a real-valued function. Then
1.
2.
3.
4.
5.
6.
(Chain Rule)
This theorem can be proved either directly from Definition 1 or by using Theorem 2 and
the corresponding differentiation formulas for real-valued functions. The proof of Formula 4
follows; the remaining proofs are left as exercises.
d
dt
关u共 f 共t兲兲兴 苷 f ⬘共t兲u⬘共 f 共t兲兲
d
dt
关u共t兲 ⫻ v共t兲兴 苷 u⬘共t兲 ⫻ v共t兲 ⫹ u共t兲 ⫻ v⬘共t兲
d
dt
关u共t兲 ⴢ v共t兲兴 苷 u⬘共t兲 ⴢ v共t兲 ⫹ u共t兲 ⴢ v⬘共t兲
d
dt
关 f 共t兲u共t兲兴 苷 f ⬘共t兲u共t兲 ⫹ f 共t兲u⬘共t兲
d
dt
关cu共t兲兴 苷 cu⬘共t兲
d
dt
关u共t兲 ⫹ v共t兲兴 苷 u⬘共t兲 ⫹ v⬘共t兲
f
cvu
3
r⬙共t兲 苷 具⫺2 cos t, ⫺sin t, 0典
r⬙ 苷 共r⬘兲⬘r⬘
FIGURE 3
z
0
12
1
0
_1
2
0
_2
y
x
8
4
_0.5
0.5
z 苷
2
⫹ ty 苷 1x 苷 ⫺2t
具⫺2, 0, 1典
共0, 1,
兾2兲r⬘共
兾2兲 苷 具⫺2, 0, 1典
t 苷
兾2共0, 1,
兾2兲
862
||||
CHAPTER 14 VECTOR FUNCTIONS
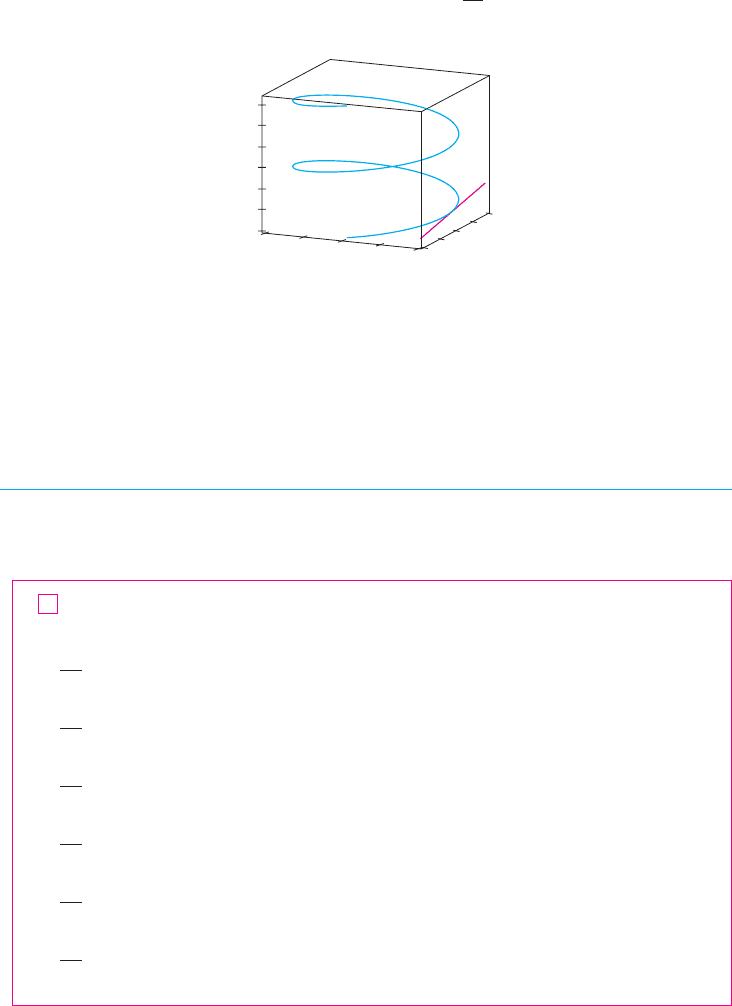
N The helix and the tangent line in Example 3
are shown in Figure 3.
N In Section 14.4 we will see how and
can be interpreted as the velocity and
acceleration vectors of a particle moving through
space with position vector at time .tr共t兲
r⬙共t兲
r⬘共t兲
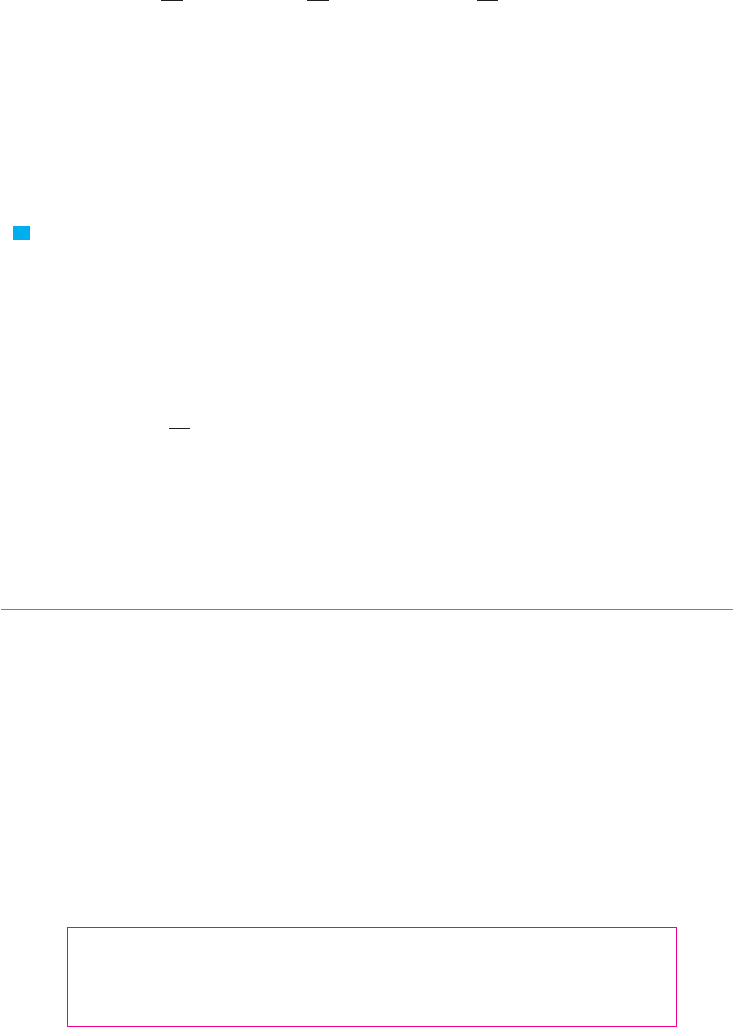
PROOF OF FORMULA 4 Let
Then
so the ordinary Product Rule gives
M
EXAMPLE 4 Show that if (a constant), then is orthogonal to for
all .
SOLUTION Since
and is a constant, Formula 4 of Theorem 3 gives
Thus , which says that is orthogonal to .
Geometrically, this result says that if a curve lies on a sphere with center the origin,
then the tangent vector is always perpendicular to the position vector . M
INTEGRALS
The definite integral of a continuous vector function can be defined in much the same
way as for real-valued functions except that the integral is a vector. But then we can
express the integral of in terms of the integrals of its component functions , , and as
follows. (We use the notation of Chapter 5.)
and so
y
b
a
r共t兲 dt 苷
冉y
b
a
f 共t兲 dt
冊
i ⫹
冉y
b
a
t共t兲 dt
冊
j ⫹
冉y
b
a
h共t兲 dt
冊
k
苷 lim
n l ⬁
冋冉
兺
n
i苷1
f 共t
*
i
兲 ⌬t
冊
i ⫹
冉
兺
n
i苷1
t共t
*
i
兲 ⌬t
冊
j ⫹
冉
兺
n
i苷1
h共t
*
i
兲 ⌬t
冊
k
册
y
b
a
r共t兲 dt 苷 lim
n l ⬁
兺
n
i苷1
r共t
*
i
兲 ⌬t
htfr
r共t兲
r共t兲r⬘共t兲
r共t兲r⬘共t兲r⬘共t兲 ⴢ r共t兲 苷 0
0 苷
d
dt
关r共t兲 ⴢ r共t兲兴 苷 r⬘共t兲 ⴢ r共t兲 ⫹ r共t兲 ⴢ r⬘共t兲 苷 2r⬘共t兲 ⴢ r共t兲
c
2
r共t兲 ⴢ r共t兲 苷
ⱍ
r共t兲
ⱍ
2
苷 c
2
t
r共t兲r⬘共t兲
ⱍ
r共t兲
ⱍ
苷 c
V
苷 u⬘共t兲 ⴢ v共t兲 ⫹ u共t兲 ⴢ v⬘共t兲
苷
兺
3
i苷1
f
⬘
i
共t兲t
i
共t兲 ⫹
兺
3
i苷1
f
i
共t兲t
⬘
i
共t兲
苷
兺
3
i苷1
关 f
⬘
i
共t兲t
i
共t兲 ⫹ f
i
共t兲t
⬘
i
共t兲兴
d
dt
关u共t兲 ⴢ v共t兲兴 苷
d
dt
兺
3
i苷1
f
i
共t兲t
i
共t兲 苷
兺
3
i苷1
d
dt
关 f
i
共t兲t
i
共t兲兴
u共t兲 ⴢ v共t兲 苷 f
1
共t兲t
1
共t兲 ⫹ f
2
共t兲t
2
共t兲 ⫹ f
3
共t兲t
3
共t兲 苷
兺
3
i苷1
f
i
共t兲t
i
共t兲
v共t兲 苷 具 t
1
共t兲, t
2
共t兲, t
3
共t兲典u共t兲 苷 具 f
1
共t兲, f
2
共t兲, f
3
共t兲典
SECTION 14.2 DERIVATIVES AND INTEGRALS OF VECTOR FUNCTIONS
||||
863
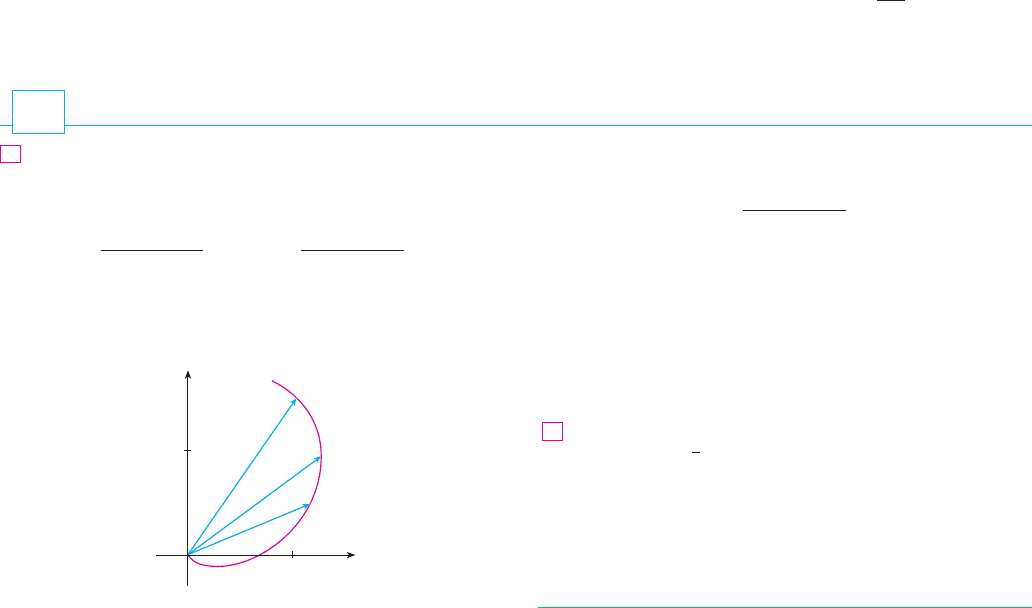
This means that we can evaluate an integral of a vector function by integrating each com-
ponent function.
We can extend the Fundamental Theorem of Calculus to continuous vector functions as
follows:
where is an antiderivative of , that is, . We use the notation for
indefinite integrals (antiderivatives).
EXAMPLE 5 If , then
where is a vector constant of integration, and
M
y
兾2
0
r共t兲 dt 苷
[
2 sin t i ⫺ cos t j ⫹ t
2
k
]
0
兾2
苷 2 i ⫹ j ⫹
2
4
k
C
苷 2 sin t i ⫺ cos t j ⫹ t
2
k ⫹ C
y
r共t兲 dt 苷
冉y
2 cos t dt
冊
i ⫹
冉y
sin t dt
冊
j ⫹
冉y
2t dt
冊
k
r共t兲 苷 2 cos t i ⫹ sin t j ⫹ 2t k
x r共t兲 dtR⬘共t兲 苷 r共t兲rR
y
b
a
r共t兲 dt 苷 R共t兲
]
b
a
苷 R共b兲 ⫺ R共a兲
864
||||
CHAPTER 14 VECTOR FUNCTIONS
(b) Draw the vector starting at (1, 1) and compare it with
the vector
Explain why these vectors are so close to each other in
length and direction.
3–8
(a) Sketch the plane curve with the given vector equation.
(b) Find .
(c) Sketch the position vector and the tangent vector for
the given value of .
,
4. ,
5. ,
6. ,
7. ,
8. ,
9–16 Find the derivative of the vector function.
9.
r共t兲 苷 具t sin t, t
2
, t cos 2t 典
t 苷
兾6r共t兲 苷 共1 ⫹ cos t兲 i ⫹ 共2 ⫹ sin t兲
j
t 苷 0r共t兲 苷 e
t
i ⫹ e
3t
j
t 苷 0r共t兲 苷 e
t
i ⫹ e
⫺t
j
t 苷
兾4r共t兲 苷 sin t i ⫹ 2 cos t
j
t 苷 1r共t兲 苷
具
1 ⫹ t,
s
t
典
t 苷 ⫺1r共t兲 苷 具t ⫺ 2, t
2
⫹ 1典
3.
t
r⬘共t兲r共t兲
r⬘共t兲
r共1.1兲 ⫺ r共1兲
0.1
r⬘共1兲
The figure shows a curve given by a vector function .
(a) Draw the vectors and .
(b) Draw the vectors
(c) Write expressions for and the unit tangent vector T(4).
(d) Draw the vector T(4).
2. (a) Make a large sketch of the curve described by the vector
function , , and draw the vectors
r(1), r(1.1), and r(1.1) ⫺ r(1).
0 艋 t 艋 2r共t兲 苷 具t
2
, t典
x
0
1
1
y
R
C
Q
P
r(4.5)
r(4.2)
r(4)
r⬘共4兲
r共4.2兲 ⫺ r共4兲
0.2
and
r共4.5兲 ⫺ r共4兲
0.5
r共4.2兲 ⫺ r共4兲r共4.5兲 ⫺ r共4兲
r共t兲C
1.
EXERCISES
14.2

33–38 Evaluate the integral.
33.
34.
35.
36.
37.
38.
39. Find if and .
40. Find if and .
41. Prove Formula 1 of Theorem 3.
42. Prove Formula 3 of Theorem 3.
43. Prove Formula 5 of Theorem 3.
44. Prove Formula 6 of Theorem 3.
45. If and , use
Formula 4 of Theorem 3 to find
46. If and are the vector functions in Exercise 45, use
Formula 5 of Theorem 3 to find
47. Show that if is a vector function such that exists, then
48. Find an expression for .
If , show that .
[
Hint:
]
50. If a curve has the property that the position vector is
always perpendicular to the tangent vector , show that
the curve lies on a sphere with center the origin.
51. If , show that
u⬘共t兲 苷 r共t兲 ⴢ 关r⬘共t兲 ⫻ r共t兲兴
u共t兲 苷 r共t兲 ⴢ 关r⬘共t兲 ⫻ r⬙共t兲兴
r⬘共t兲
r共t兲
ⱍ
r共t兲
ⱍ
2
苷 r共t兲 ⴢ r共t兲
d
dt
ⱍ
r共t兲
ⱍ
苷
1
ⱍ
r共t兲
ⱍ
r共t兲 ⴢ r⬘共t兲r共t兲 苷 0
49.
d
dt
关u共t兲 ⴢ 共v共t兲 ⫻ w共t兲兲兴
d
dt
关r共t兲 ⫻ r⬘共t兲兴 苷 r共t兲 ⫻ r⬙共t兲
r⬙r
d
dt
关u共t兲 ⫻ v共t兲兴
vu
d
dt
关u共t兲 ⴢ v共t兲兴
v共t兲 苷 具t, cos t, sin t典u共t兲 苷 具sin t, cos t, t典
r共0兲 苷 i ⫹ j ⫹ kr⬘共t兲 苷 t i ⫹ e
t
j ⫹ te
t
kr共t兲
r共1兲 苷 i ⫹ jr⬘共t兲 苷 2t
i ⫹ 3t
2
j ⫹
s
t
kr共t兲
y
共cos
t i ⫹ sin
t j ⫹ t k兲 dt
y
共e
t
i ⫹ 2t j ⫹ ln t k兲 dt
y
2
1
(
t
2
i ⫹ t
s
t ⫺ 1 j ⫹ t sin
t k
)
dt
y
兾2
0
共3 sin
2
t cos t i ⫹ 3 sin t cos
2
t j ⫹ 2 sin t cos t k兲 dt
y
1
0
冉
4
1 ⫹ t
2
j ⫹
2t
1 ⫹ t
2
k
冊
dt
y
1
0
共16t
3
i ⫺ 9t
2
j ⫹ 25t
4
k兲 dt
10.
11.
12.
13.
14.
16.
17–20 Find the unit tangent vector at the point with the
given value of the parameter .
17.
,
18.
,
,
20. ,
21. If , find and
22. If , find , , and
23–26 Find parametric equations for the tangent line to the curve
with the given parametric equations at the specified point.
23. ,,;
24. ,, ;
,,;
26. ,,;
;
27–29 Find parametric equations for the tangent line to the
curve with the given parametric equations at the specified point.
Illustrate by graphing both the curve and the tangent line on a
common screen.
27. ,, ;
28. ,, ;
29. ,, ;
30. (a) Find the point of intersection of the tangent lines to the
curve at the points
where and .
;
(b) Illustrate by graphing the curve and both tangent lines.
31. The curves and
intersect at the origin. Find their angle of intersection correct
to the nearest degree.
32. At what point do the curves and
intersect? Find their angle of
intersection correct to the nearest degree.
r
2
共s兲 苷 具3 ⫺ s, s ⫺ 2, s
2
典
r
1
共t兲 苷 具t, 1 ⫺ t, 3 ⫹ t
2
典
r
2
共t兲 苷 具sin t, sin 2t, t 典r
1
共t兲 苷 具t, t
2
, t
3
典
t 苷 0.5t 苷 0
r共t兲 苷 具sin
t, 2 sin
t, cos
t典
共⫺
,
, 0兲z 苷 t sin ty 苷 tx 苷 t cos t
(
s
3
, 1, 2
)
z 苷 4 cos 2ty 苷 2 sin tx 苷 2 cos t
共0, 1, 0兲z 苷 2t ⫺ t
2
y 苷 e
⫺t
x 苷 t
共0, 2, 1兲z 苷 t
2
y 苷 2
s
t
x 苷 ln t
共1, 0, 1兲z 苷 e
⫺t
y 苷 e
⫺t
sin tx 苷 e
⫺t
cos t
25.
共1, 0, 0兲z 苷 te
t
2
y 苷 te
t
x 苷 e
t
共3, 0, 2兲z 苷 t
3
⫹ ty 苷 t
3
⫺ tx 苷 1 ⫹ 2
s
t
r⬘共t兲 ⴢ r⬙共t兲.r⬙共0兲T共0兲r共t兲 苷 具e
2t
, e
⫺2t
, te
2t
典
r⬘共t兲 ⫻ r⬙共t兲.r⬘共t兲, T共1兲, r⬙共t兲, r共t兲 苷 具t, t
2
, t
3
典
t 苷
兾4r共t兲 苷 2 sin t i ⫹ 2 cos t j ⫹ tan t k
t 苷 0r共t兲 苷 cos t i ⫹ 3t j ⫹ 2 sin 2t k
19.
t 苷 1r共t兲 苷 4
s
t
i ⫹ t
2
j ⫹ t k
t 苷 0r共t兲 苷 具te
⫺t
, 2 arctan t, 2e
t
典
t
T共t兲
r共t兲 苷 t a ⫻ 共b ⫹ t c兲
r共t兲 苷 a ⫹ t b ⫹ t
2
c
15.
r共t兲 苷 at cos 3t i ⫹ b sin
3
t j ⫹ c cos
3
t k
r共t兲 苷 e
t
2
i ⫺ j ⫹ ln共1 ⫹ 3t兲
k
r共t兲 苷 sin
⫺1
t i ⫹
s
1 ⫺ t
2
j ⫹ k
r共t兲 苷 i ⫺ j ⫹ e
4t
k
r共t兲 苷 具tan t, sec t, 1兾t
2
典
SECTION 14.2 DERIVATIVES AND INTEGRALS OF VECTOR FUNCTIONS
||||
865
ARC LENGTH AND CURVATURE
In Section 11.2 we defined the length of a plane curve with parametric equations ,
, , as the limit of lengths of inscribed polygons and, for the case where
and are continuous, we arrived at the formula
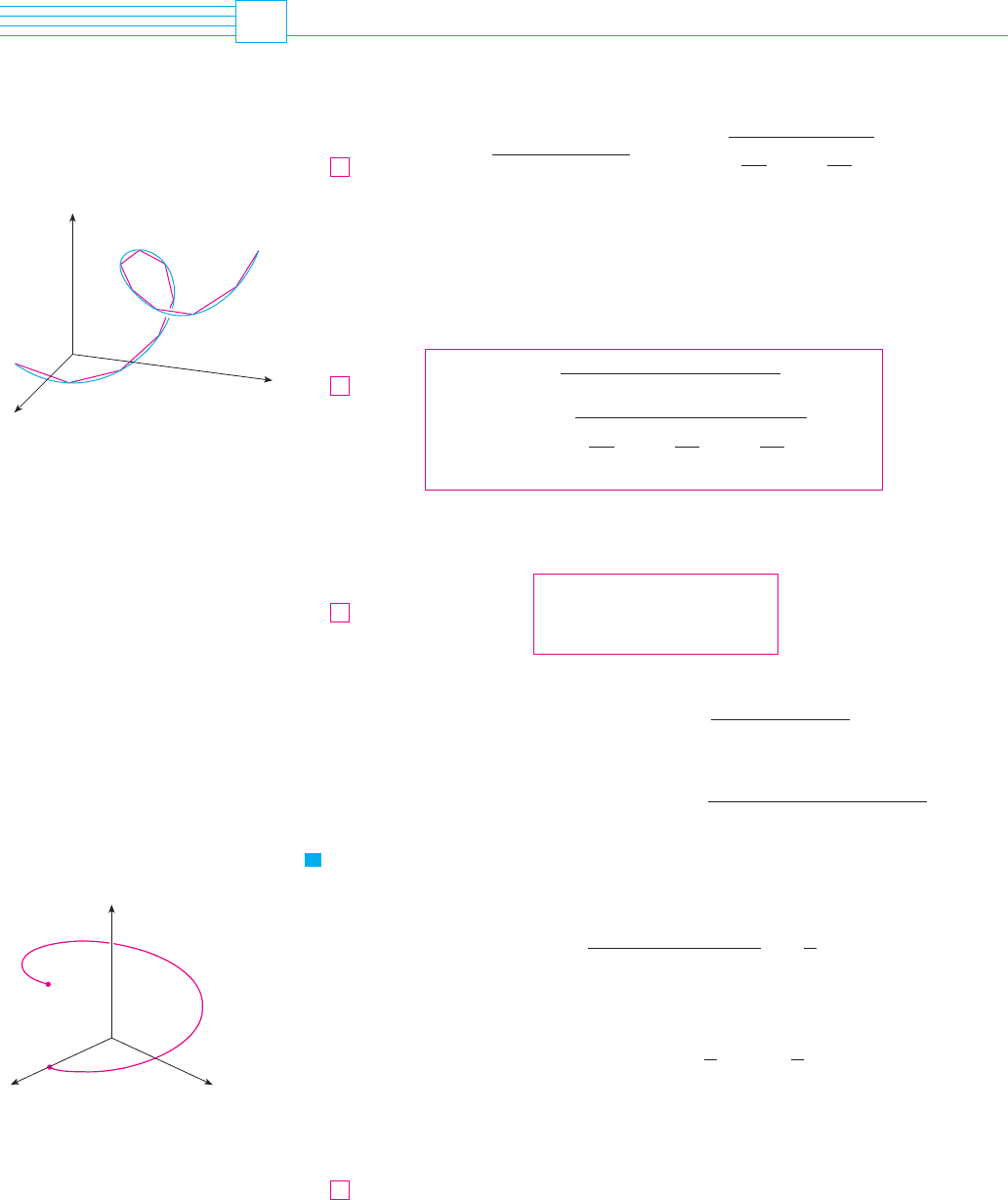
The length of a space curve is defined in exactly the same way (see Figure 1). Suppose
that the curve has the vector equation , , or, equivalently,
the parametric equations , , , where , , and are continuous.
If the curve is traversed exactly once as increases from to , then it can be shown that
its length is
Notice that both of the arc length formulas (1) and (2) can be put into the more com-
pact form
because, for plane curves ,
and for space curves ,
EXAMPLE 1 Find the length of the arc of the circular helix with vector equation
from the point to the point .
SOLUTION Since , we have
The arc from to is described by the parameter interval
and so, from Formula 3, we have
M
A single curve can be represented by more than one vector function. For instance, the
twisted cubic
1 艋 t 艋 2r
1
共t兲 苷 具t, t
2
, t
3
典
4
C
L 苷
y
2
0
ⱍ
r⬘共t兲
ⱍ
dt 苷
y
2
0
s
2
dt 苷 2
s
2
0 艋 t 艋 2
共1, 0, 2
兲共1, 0, 0兲
ⱍ
r⬘共t兲
ⱍ
苷
s
共⫺sin t兲
2
⫹ cos
2
t ⫹ 1 苷
s
2
r⬘共t兲 苷 ⫺sin t i ⫹ cos t j ⫹ k
共1, 0, 2
兲共1, 0, 0兲r共t兲 苷 cos t i ⫹ sin t j ⫹ t k
V
ⱍ
r⬘共t兲
ⱍ
苷
ⱍ
f ⬘共t兲i ⫹ t⬘共t兲 j ⫹ h⬘共t兲 k
ⱍ
苷
s
关 f ⬘共t兲兴
2
⫹ 关t⬘共t兲兴
2
⫹ 关h⬘共t兲兴
2
r共t兲 苷 f 共t兲i ⫹ t共t兲j ⫹ h共t兲 k
ⱍ
r⬘共t兲
ⱍ
苷
ⱍ
f ⬘共t兲i ⫹ t⬘共t兲 j
ⱍ
苷
s
关 f ⬘共t兲兴
2
⫹ 关t⬘共t兲兴
2
r共t兲 苷 f 共t兲i ⫹ t共t兲j
L 苷
y
b
a
ⱍ
r⬘共t兲
ⱍ
dt
3
苷
y
b
a
冑
冉
dx
dt
冊
2
⫹
冉
dy
dt
冊
2
⫹
冉
dz
dt
冊
2
dt
L 苷
y
b
a
s
关 f ⬘共t兲兴
2
⫹ 关t⬘共t兲兴
2
⫹ 关h⬘共t兲兴
2
dt
2
bat
h⬘t⬘f ⬘z 苷 h共t兲y 苷 t共t兲x 苷 f 共t兲
a 艋 t 艋 br共t兲 苷 具 f 共t兲, t共t兲, h共t兲典
L 苷
y
b
a
s
关 f ⬘共t兲兴
2
⫹ 关t⬘共t兲兴
2
dt 苷
y
b
a
冑
冉
dx
dt
冊
2
⫹
冉
dy
dt
冊
2
dt
1
t⬘f ⬘
a 艋 t 艋 by 苷 t共t兲
x 苷 f 共t兲
14.3
866
||||
CHAPTER 14 VECTOR FUNCTIONS
FIGURE 1
The length of a space curve is the limit
of lengths of inscribed polygons.
0
z
x
y
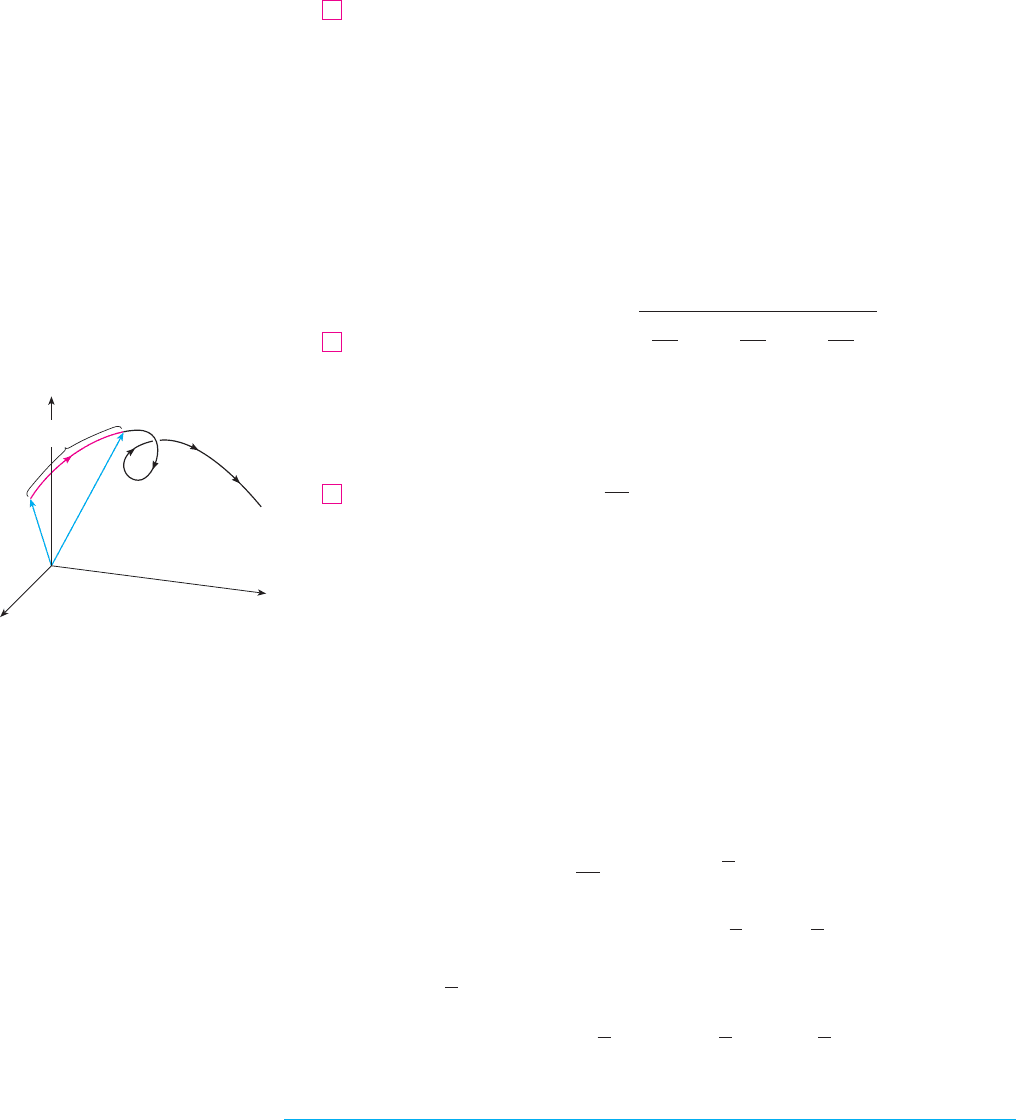
N Figure 2 shows the arc of the helix
whose length is computed in Example 1.
FIGURE 2
(1,0,2π)
z
x
y
(1,0,0)
could also be represented by the function
where the connection between the parameters and is given by . We say that
Equations 4 and 5 are parametrizations of the curve . If we were to use Equation 3 to
compute the length of using Equations 4 and 5, we would get the same answer. In gen-
eral, it can be shown that when Equation 3 is used to compute arc length, the answer is
independent of the parametrization that is used.
Now we suppose that is a curve given by a vector function
where is continuous and is traversed exactly once as increases from to . We define
its arc length function by
Thus is the length of the part of between and . (See Figure 3.) If we differ-
entiate both sides of Equation 6 using Part 1 of the Fundamental Theorem of Calculus, we
obtain
It is often useful to parametrize a curve with respect to arc length because arc length
arises naturally from the shape of the curve and does not depend on a particular coordinate
system. If a curve is already given in terms of a parameter and is the arc length
function given by Equation 6, then we may be able to solve for as a function of :
Then the curve can be reparametrized in terms of by substituting for : . Thus,
if for instance, is the position vector of the point 3 units of length along the
curve from its starting point.
EXAMPLE 2 Reparametrize the helix with respect to arc
length measured from in the direction of increasing .
SOLUTION The initial point corresponds to the parameter value . From
Example 1 we have
and so
Therefore and the required reparametrization is obtained by substituting for :
M
CURVATURE
A parametrization is called smooth on an interval if is continuous and
on . A curve is called smooth if it has a smooth parametrization. A smooth curve has no
sharp corners or cusps; when the tangent vector turns, it does so continuously.
I
r⬘共t兲 苷 0r⬘Ir共t兲
r共t共s兲兲 苷 cos
(
s兾
s
2
)
i ⫹ sin
(
s兾
s
2
)
j ⫹
(
s兾
s
2
)
k
tt 苷 s兾
s
2
s 苷 s共t兲 苷
y
t
0
ⱍ
r⬘共u兲
ⱍ
du 苷
y
t
0
s
2
du 苷
s
2
t
ds
dt
苷
ⱍ
r⬘共t兲
ⱍ
苷
s
2
t 苷 0共1, 0, 0兲
t共1, 0, 0兲
r共t兲 苷 cos t i ⫹ sin t j ⫹ t k
r共t共3兲兲s 苷 3
r 苷 r共t共s兲兲ts
t 苷 t共s兲.st
s共t兲tr共t兲
ds
dt
苷
ⱍ
r⬘共t兲
ⱍ
7
r共t兲r共a兲Cs共t兲
s共t兲 苷
y
t
a
ⱍ
r⬘共u兲
ⱍ
du 苷
y
t
a
冑
冉
dx
du
冊
2
⫹
冉
dy
du
冊
2
⫹
冉
dz
du
冊
2
du
6
s
batCr⬘
a 艋 t 艋 br共t兲 苷 f 共t兲i ⫹ t共t兲j ⫹ h共t兲k
C
C
C
t 苷 e
u
ut
0 艋 u 艋 ln 2r
2
共u兲 苷 具e
u
, e
2u
, e
3u
典
5
SECTION 14.3 ARC LENGTH AND CURVATURE
||||
867
FIGURE 3
z
0
x
y
C
r(t)
r(a)
s(t)

If is a smooth curve defined by the vector function , recall that the unit tangent vec-
tor is given by
and indicates the direction of the curve. From Figure 4 you can see that changes direc-
tion very slowly when is fairly straight, but it changes direction more quickly when
bends or twists more sharply.
The curvature of at a given point is a measure of how quickly the curve changes direc-
tion at that point. Specifically, we define it to be the magnitude of the rate of change of the
unit tangent vector with respect to arc length. (We use arc length so that the curvature will
be independent of the parametrization.)
DEFINITION The curvature of a curve is
where is the unit tangent vector.
The curvature is easier to compute if it is expressed in terms of the parameter instead
of , so we use the Chain Rule (Theorem 14.2.3, Formula 6) to write
But from Equation 7, so
EXAMPLE 3 Show that the curvature of a circle of radius is .
SOLUTION We can take the circle to have center the origin, and then a parametrization is
Therefore
so
and
This gives , so using Equation 9, we have
M
The result of Example 3 shows that small circles have large curvature and large circles
have small curvature, in accordance with our intuition. We can see directly from the defi-
共t兲 苷
ⱍ
T⬘共t兲
ⱍ
ⱍ
r⬘共t兲
ⱍ
苷
1
a
ⱍ
T⬘共t兲
ⱍ
苷 1
T⬘共t兲 苷 ⫺cos t i ⫺ sin t j
T共t兲 苷
r⬘共t兲
ⱍ
r⬘共t兲
ⱍ
苷 ⫺sin t i ⫹ cos t j
ⱍ
r⬘共t兲
ⱍ
苷 aandr⬘共t兲 苷 ⫺a sin t i ⫹ a cos t j
r共t兲 苷 a cos t i ⫹ a sin t j
1兾aa
V
共t兲 苷
ⱍ
T⬘共t兲
ⱍ
ⱍ
r⬘共t兲
ⱍ
9
ds兾dt 苷
ⱍ
r⬘共t兲
ⱍ
苷
冟
dT
ds
冟
苷
冟
dT兾dt
ds兾dt
冟
and
dT
dt
苷
dT
ds
ds
dt
s
t
T
苷
冟
dT
ds
冟
8
C
CC
T共t兲
T共t兲 苷
r⬘共t兲
ⱍ
r⬘共t兲
ⱍ
T共t兲
rC
868
||||
CHAPTER 14 VECTOR FUNCTIONS
FIGURE 4
Unit tangent vectors at equally spaced
points on C
z
0
x
y
C
Visual 14.3A shows animated unit
tangent vectors, like those in Figure 4, for
a variety of plane curves and space curves.
TEC

nition of curvature that the curvature of a straight line is always 0 because the tangent vec-
tor is constant.
Although Formula 9 can be used in all cases to compute the curvature, the formula
given by the following theorem is often more convenient to apply.
THEOREM The curvature of the curve given by the vector function is
PROOF Since and , we have
so the Product Rule (Theorem 14.2.3, Formula 3) gives
Using the fact that (see Example 2 in Section 13.4), we have
Now for all , so and are orthogonal by Example 4 in Section 14.2.
Therefore, by Theorem 13.4.6,
Thus
and M
EXAMPLE 4 Find the curvature of the twisted cubic at a general point
and at .
SOLUTION We first compute the required ingredients:
ⱍ
r⬘共t兲 ⫻ r⬙共t兲
ⱍ
苷
s
36t
4
⫹ 36t
2
⫹ 4
苷 2
s
9t
4
⫹ 9t
2
⫹ 1
r⬘共t兲 ⫻ r⬙共t兲 苷
ⱍ
i
1
0
j
2t
2
k
3t
2
6t
ⱍ
苷 6t
2
i ⫺ 6t j ⫹ 2k
ⱍ
r⬘共t兲
ⱍ
苷
s
1 ⫹ 4t
2
⫹ 9t
4
r⬙共t兲 苷 具0, 2, 6t典 r⬘共t兲 苷 具1, 2t, 3t
2
典
共0, 0, 0兲
r共t兲 苷 具t, t
2
, t
3
典
苷
ⱍ
T⬘
ⱍ
ⱍ
r⬘
ⱍ
苷
ⱍ
r⬘⫻r⬙
ⱍ
ⱍ
r⬘
ⱍ
3
ⱍ
T⬘
ⱍ
苷
ⱍ
r⬘⫻r⬙
ⱍ
共ds兾dt兲
2
苷
ⱍ
r⬘⫻r⬙
ⱍ
ⱍ
r⬘
ⱍ
2
ⱍ
r⬘⫻r⬙
ⱍ
苷
冉
ds
dt
冊
2
ⱍ
T ⫻ T⬘
ⱍ
苷
冉
ds
dt
冊
2
ⱍ
T
ⱍⱍ
T⬘
ⱍ
苷
冉
ds
dt
冊
2
ⱍ
T⬘
ⱍ
T⬘Tt
ⱍ
T共t兲
ⱍ
苷 1
r⬘⫻r⬙ 苷
冉
ds
dt
冊
2
共T ⫻ T⬘兲
T ⫻ T 苷 0
r⬙ 苷
d
2
s
dt
2
T ⫹
ds
dt
T⬘
r⬘ 苷
ⱍ
r⬘
ⱍ
T 苷
ds
dt
T
ⱍ
r⬘
ⱍ
苷 ds兾dtT 苷 r⬘兾
ⱍ
r⬘
ⱍ
共t兲 苷
ⱍ
r⬘共t兲 ⫻ r⬙共t兲
ⱍ
ⱍ
r⬘共t兲
ⱍ
3
r
10
SECTION 14.3 ARC LENGTH AND CURVATURE
||||
869
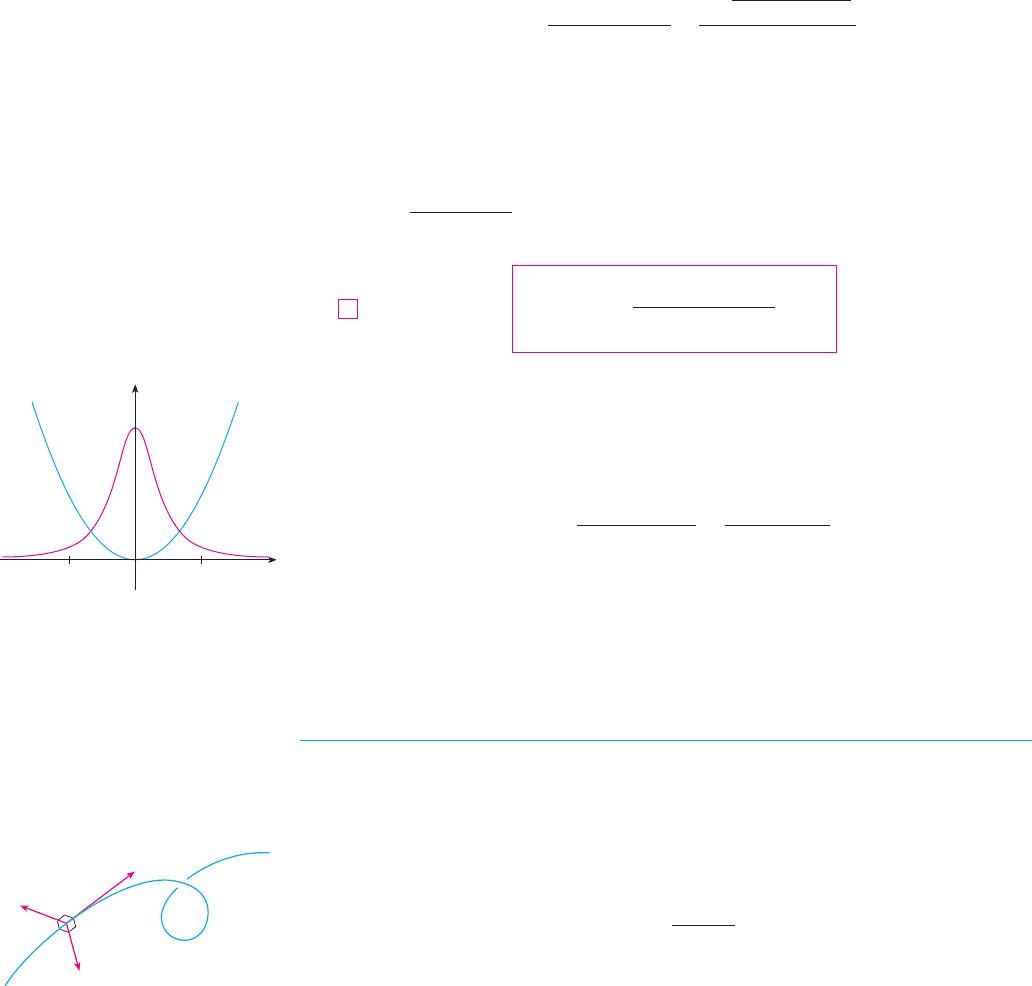
Theorem 10 then gives
At the origin, where , the curvature is .
M
For the special case of a plane curve with equation , we choose as the
parameter and write . Then and .
Since and , we have . We also have
and so, by Theorem 10,
EXAMPLE 5 Find the curvature of the parabola at the points , ,
and .
SOLUTION Since and , Formula 11 gives
The curvature at is . At it is . At it is
. Observe from the expression for or the graph of in Fig-
ure 5 that as . This corresponds to the fact that the parabola appears
to become flatter as . M
THE NORMAL AND BINORMAL VECTORS
At a given point on a smooth space curve , there are many vectors that are orthogonal
to the unit tangent vector . We single out one by observing that, because
for all , we have by Example 4 in Section 14.2, so is orthogonal to
. Note that is itself not a unit vector. But if is also smooth, we can define the
principal unit normal vector (or simply unit normal) as
The vector is called the binormal vector. It is perpendicular to both
and and is also a unit vector. (See Figure 6.)
EXAMPLE 6 Find the unit normal and binormal vectors for the circular helix
r共t兲 苷 cos t i ⫹ sin t j ⫹ t k
N
TB共t兲 苷 T共t兲 ⫻ N共t兲
N共t兲 苷
T⬘共t兲
ⱍ
T⬘共t兲
ⱍ
N共t兲
r⬘T⬘共t兲T共t兲
T⬘共t兲T共t兲 ⴢ T⬘共t兲 苷 0t
ⱍ
T共t兲
ⱍ
苷 1T共t兲
r共t兲
x l ⫾⬁
x l ⫾⬁
共x兲 l 0
共x兲
共2兲 苷 2兾17
3兾2
⬇ 0.03
共2, 4兲
共1兲 苷 2兾5
3兾2
⬇ 0.18共1, 1兲
共0兲 苷 2共0, 0兲
共x兲 苷
ⱍ
y⬙
ⱍ
关1 ⫹ 共y⬘兲
2
兴
3兾2
苷
2
共1 ⫹ 4x
2
兲
3兾2
y⬙ 苷 2y⬘ 苷 2x
共2, 4兲
共1, 1兲共0, 0兲y 苷 x
2
共x兲 苷
ⱍ
f ⬙共x兲
ⱍ
关1 ⫹ 共 f ⬘共x兲兲
2
兴
3兾2
11
ⱍ
r⬘共x兲
ⱍ
苷
s
1 ⫹ 关 f ⬘共x兲兴
2
r⬘共x兲 ⫻ r⬙共x兲 苷 f ⬙共x兲 kj ⫻ j 苷 0i ⫻ j 苷 k
r⬙共x兲 苷 f ⬙共x兲 jr⬘共x兲 苷 i ⫹ f ⬘共x兲 jr共x兲 苷 x i ⫹ f 共x兲 j
xy 苷 f 共x兲
共0兲 苷 2t 苷 0
共t兲 苷
ⱍ
r⬘共t兲 ⫻ r⬙共t兲
ⱍ
ⱍ
r⬘共t兲
ⱍ
3
苷
2
s
1 ⫹ 9t
2
⫹ 9t
4
共1 ⫹ 4t
2
⫹ 9t
4
兲
3兾2
870
||||
CHAPTER 14 VECTOR FUNCTIONS
FIGURE 5
The parabola y=≈ and its
curvature function
2
1
x
0
y
y=≈
y=k(x)
N We can think of the normal vector as indi-
cating the direction in which the curve is
turning at each point.
N(t)
T(t)
B(t)
FIGURE 6

SOLUTION We first compute the ingredients needed for the unit normal vector:
This shows that the normal vector at a point on the helix is horizontal and points toward
the -axis. The binormal vector is
M
The plane determined by the normal and binormal vectors and at a point on a
curve is called the normal plane of at . It consists of all lines that are orthogonal
to the tangent vector . The plane determined by the vectors and is called the oscu-
lating plane of at . The name comes from the Latin osculum, meaning “kiss.” It is the
plane that comes closest to containing the part of the curve near . (For a plane curve, the
osculating plane is simply the plane that contains the curve.)
The circle that lies in the osculating plane of at , has the same tangent as at , lies
on the concave side of (toward which points), and has radius (the reciprocal
of the curvature) is called the osculating circle (or the circle of curvature) of at . It is
the circle that best describes how behaves near ; it shares the same tangent, normal,
and curvature at .
EXAMPLE 7 Find the equations of the normal plane and osculating plane of the helix
in Example 6 at the point .
SOLUTION The normal plane at has normal vector , so an equation
is
The osculating plane at contains the vectors and , so its normal vector is
. From Example 6 we have
A simpler normal vector is , so an equation of the osculating plane is
M
z 苷 ⫺x ⫹
2
or1共x ⫺ 0兲 ⫹ 0共y ⫺ 1兲 ⫹ 1
冉
z ⫺
2
冊
苷 0
具1, 0, 1典
B
冉
2
冊
苷
冓
1
s
2
, 0,
1
s
2
冔
B共t兲 苷
1
s
2
具sin t, ⫺cos t, 1典
T ⫻ N 苷 B
NTP
z 苷 x ⫹
2
or⫺1共x ⫺ 0兲 ⫹ 0共y ⫺ 1兲 ⫹ 1
冉
z ⫺
2
冊
苷 0
r⬘共
兾2兲 苷 具⫺1, 0, 1典P
P共0, 1,
兾2兲
V
P
PC
PC
苷 1兾
NC
PCPC
P
PC
NTT
PCC
PBN
苷
1
s
2
具sin t, ⫺cos t, 1典B共t兲 苷 T共t兲 ⫻ N共t兲 苷
1
s
2
冋
i
⫺sin t
⫺cos t
j
cos t
⫺sin t
k
1
0
册
z
N共t兲 苷
T⬘共t兲
ⱍ
T⬘共t兲
ⱍ
苷 ⫺cos t i ⫺ sin t j 苷 具⫺cos t, ⫺sin t, 0典
ⱍ
T⬘共t兲
ⱍ
苷
1
s
2
T⬘共t兲 苷
1
s
2
共⫺cos t i ⫺ sin t j兲
T共t兲 苷
r⬘共t兲
ⱍ
r⬘共t兲
ⱍ
苷
1
s
2
共⫺sin t i ⫹ cos t j ⫹ k兲
ⱍ
r⬘共t兲
ⱍ
苷
s
2
r⬘共t兲 苷 ⫺sin t i ⫹ cos t j ⫹ k
SECTION 14.3 ARC LENGTH AND CURVATURE
||||
871
N Figure 7 illustrates Example 6 by showing
the vectors , , and at two locations on the
helix. In general, the vectors , , and , start-
ing at the various points on a curve, form a set of
orthogonal vectors, called the frame, that
moves along the curve as varies. This
frame plays an important role in the branch of
mathematics known as differential geometry and
in its applications to the motion of spacecraft.
TNBt
TNB
BNT
BNT
N
N
B
T
T
B
FIGURE 7
x
y
z
Visual 14.3B shows how the TNB
frame moves along several curves.
TEC
FIGURE 8
y
P
x
z=_x+
π
2
z
N Figure 8 shows the helix and the osculating
plane in Example 7.
