Sundararaja D. The Discrete Fourier Transform. Theory, Algorithms and Applications

194

DFT Algorithms for Real Data - II

processing tends to become a smaller proportion of the total com-

plexity.

• Between algorithms of the same order of complexity, in general,

the algorithm with better regularity should be preferred even if it

requires slightly more number of arithmetic operations as irregular-

ity also increases execution time in terms of overhead operations.

Therefore, for large N, the indirect use of algorithms for complex

data is preferred. For small N, PM RDFT and PM RIDFT algo-

rithms are preferred, since the arithmetic advantage is significant

and the irregularity may not be a problem as the algorithm can be

implemented as one block in hardware or software. While the user

has to make the final choice for a specific application, we recom-

mend the PM RDFT and PM RIDFT algorithms for N less than

or equal to 16 and the indirect use of algorithms for complex data

for N greater than or equal to 32.

References

(1) Sundararajan, D., Ahmad, M. O. and Swamy, M. N. S. (1994)

"Computational Structures for Fast Fourier Transform Analyzers",

U.S. Patent, No. 5,371,696.

(2) Sundararajan, D., Ahmad, M. O. and Swamy, M. N. S. (1997)

"Fast Computation of the discrete Fourier Transform of Real Data",

IEEE Trans. Signal Processing, vol. 45, No. 8, pp. 2010-2022.

Programming Exercises

9.1 Write a 3-butterfly program to implement the 2 x 1 PM DIT RDFT

algorithm.

9.2 Write a 3-butterfly program to implement the 2 x 1 PM DIF RIDFT

algorithm.

9.3 Write a 3-butterfly program to implement the 2 x 2 PM DIT RDFT

algorithm.

9.4 Write a 3-butterfly program to implement the 2 x 2 PM DIF RIDFT

algorithm.

Chapter 10

Two-Dimensional Discrete Fourier

Transform

The theory of 2-D signals, for the most part, is a straightforward extension

of the theory of 1-D signals. In this chapter, we refer to the spatial time-

domain 2-D discrete signal as image. In Sec. 10.1, the definitions of 2-D

DFT and IDFT are given. In Sec. 10.2, the physical interpretation of

2-D DFT is presented. The DFT of some simple 2-D signals are derived

analytically. In Sec. 10.3, the row-column approach of computing the 2-D

DFT is described. The properties and theorems of 2-D DFT are presented

in Sec. 10.4. The 2-D PM DFT algorithms are developed in Sec. 10.5.

10.1 The 2-D DFT and IDFT

The 2-D DFT of an

iV

x

JV

image (for simplicity, we assume that, unless oth-

erwise stated, the dimensions are the same in the two directions) {x(ni, n

2

),

ni,

n

2

=

0,1,...,

N

—

1} is defined as

JV-l N-l

X(k

u

k

2

)=Y,

E

x

(

ni

'

ri2

W*

1

^

2

^i^2=0,l,-,iV-l (10.1)

ni=0 ri2=0

The 2-D IDFT is defined as

.. N-l N-l

*(m,na) = j^Y,

J2

X

^

k

^

W

N

nikxW

N

n2k2

^

ki =0ifc

2

=0

ni,n

2

=0,1,...,7V-1 (10.2)

195

196

Two-Dimensional Discrete Fourier Transform

Center-zero format of the 2-D DFT and IDFT

The 2-D DFT, in the center-zero format with N even, is defined as

X(k

u

k

2

) = £ E

<ri

u

n

2

)W^W^

k

\

«! =

-«-

712

N N

-,

N

,

The 2-D IDFT, in the center-zero format with N even, is defined as

*(m,n

2

) = 4 E E ^i-M^"

1

*

1

^"

2

*

2

,

«1——"2"

«2

——"2"

N N , N

n

1

,n

2

= -

T

,-y +

l,...,

y

-l

Getting one format from the other involves the swapping of the quadrants

of the image or the spectrum.

10.2 DFT Representation of Some 2-D Signals

The physical interpretation of the 1-D DFT representation of a signal is that

the signal, which is a curve, is a linear combination of a set of sinusoidal

curves of various frequencies, phase shifts, and amplitudes. The physical

interpretation of the 2-D DFT representation of a signal is that the signal,

which is a surface, is a linear combination of a set of sinusoidal surfaces

of various frequencies, phase shifts, amplitudes, and directions. Given an

image, therefore, the problem of Fourier analysis is the determination of the

coefficients of its constituent sinusoidal surfaces. The problem of Fourier

synthesis is, given the coefficients of a set of sinusoidal surfaces, the building

of the corresponding image. A sinusoidal surface is a stack of shifted

sinusoidal waveforms of the same amplitude and frequency. Assuming N

is even, the constituent sinusoidal surfaces of a real image is obtained from

Eq. (10.2).

x(n

u

n

2

) =

j^{X(0,0)

+ X{-, 0) cos{-K

ni

) + X(0, -) cos(7m

2

)

+ X{-^, y) cos(7r(ni + n

2

))

DFT Representation

of

Some

2-D

Signals

197

*

_1

27T

+

2 J2

(l*(*i.O)| cos(— mfci

+

Z(X(fc!,0)))

2

27T

+

2 ^

(|X(0,fc

2

)| cos( —

n

2

fc

2

+

Z(X(0,

fe)))

fe

2

=i

N

y

N 2ir N N

+ 2^(|X(

Y

,fc

2

)|cos(-(n

1

-

+

n

2

fc

2

)

+

Z(X(-,fe

2

)))

fc

2

=i

+

2 ^

^(|X(fc

1

,fc

2

)|cos(-^(n

1

fc

1

+n

2

fe

2

)

+

Z(X(fc

1

,A

;2

)))},

fc

1=

ifc

2

=i

m,n

2

=

0,l,...,iV-l (10.3)

Note that X(0,0),X(f ,0),X(0, f

),X(f,

f) are

real

for

real images.

Therefore,

an N x N

real image, where

TV is

even, consists

of ^- + 2

sinusoidal surfaces.

To

avoid

the

aliasing effect,

the

indices,

fci and fc

2

, of

the constituent frequency components

of a 2-D

signal must

be

less than

y.

Note that

in Eq.

(10.3),

we

have used

the

coefficients

of the

upper half

of

the spectrum

but the

left half also will

do.

The

DFT of

x(ni,n

2

)

=

<5(rii,n

2

)

is

given

by

o

X(k

1

,k

2

)= ^2 53

X = 1 and

S(ni,n

2

)<$l

m=0n

2

=0

Since

the

impulse signal

is

zero except with

n\ = 0 and n

2

= 0, for all

&i,fc

2

,

the DFT

coefficient

is

unity.

Example

10.1

Identify

the

sinusoidal surfaces that constitute

the 4x4

impulse signal.

Solution

Figures 10.1(a)

and (b)

show, respectively,

the 2-D

impulse signal

and its

spectrum.

(In the

representation

of the

image matrix,

we

assume, unless

otherwise stated, that

the

origin

is at the

upper left-hand corner.

The

index

ni increases downward

and the

index

n

2

increases

to the

right.)

All the

frequency components exist

and

have equal amplitude

and

zero phase.

In

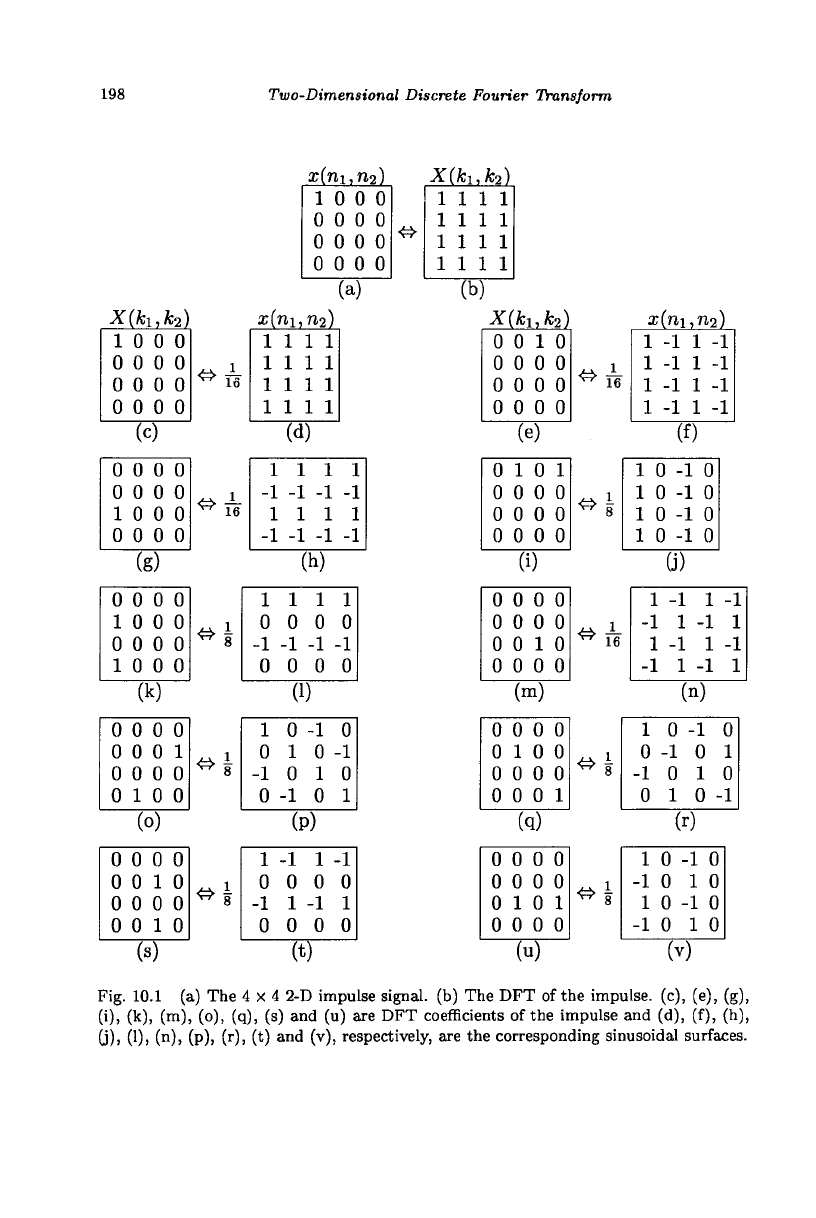
198 Two-Dimensional Discrete Fourier Transform

X(h

1 0

0 0

7*2)

0 0

(c)

(g)

(k)

0

1

0

1

0

(o)

0 0

0

rH

0

rH

0

(s)

*>TS

0

1

0

<$

0

1

0

1

0

W

8

<S>

<$

x{

1

0

rc,

0

,n

2

)

0

(a)

x(ni,n

2

)

1-H

1

rH

1

rH

1-H

1

h-i

1

(d)

1

16

rH

-1

1

-1

1

-1

1

-1

1

-1

1

-1

-

-1

1

-1

(h)

1-H

0

-1

0

1

0

-1

0

1 1

0 0

-1 -1

0 0

(1)

1

8

1

0

-1

0

1

0

-1

0

1

0

-1

0

1

(p)

1

0

-1

0

-1

0

1

0

rH

0

-1

0

T

0

1

0

(t)

t>

X(kufa)

1111

(b)

X

0

(*

0

,fc

2

)

1 0

0 0

(e)

0

1

0

1

0

(i)

0

1

0

(m)

0

1

0

1

(q)

0

1

0

1

0

(u)

w

16

<S>

w

16

<£>

s(ni,n

2

)

1

-1 1

-1

(f)

1

0

-1

0

(j)

1

-1

1

-1

1

-1

1

1-H

-1

1

-1

1

-1

1

(n)

1

8

1

0

-1

0

0 -1

-1 0

0 1

1 0

0

1-H

0

-1

(r)

1

-1

1

-1

0

-1

1

-1

1

0

(v)

Fig. 10.1 (a) The 4 x 4 2-D impulse signal, (b) The DFT of the impulse, (c), (e), (g),

(i),

(k), (m), (o), (q), (s) and (u) are DFT coefficients of the impulse and (d), (f), (h),

0)i (')> (

n

)>

(P)>

(

r

)> M

an

^ (

v

)> respectively, are the corresponding sinusoidal surfaces.

DFT Representation of Some 2-D Signals

199

terms of complex exponentials, the impulse signal is represented as

3 3

*(ni,«2) = i£ ^

e

i»f(m*

1

+n

9

fa)

> ni

,

n2=

0,1,2,3

kr =0*2=0

We can find the real sinusoidal surfaces that constitute the impulse signal

using this equation or Eq. (10.3) with N = 4. Each separate frequency

coefficient or a pair and the corresponding sinusoidal surface are shown in

Figs.

10.1(c) to (v).

Figure 10.1(c) shows X(0,0) = 1 and the corresponding surface is the dc

component having sample value i- at all points, shown in Fig. 10.1(d).

Figure 10.1(e) shows X(0,2) = 1 and the corresponding surface is ^ cos(7rn

2

),

shown in Fig. 10.1(f). This is a stack, in the vertical direction, of four co-

sine waveforms with frequency index two.

Figure 10.1(k) shows X(1,0) =

1,X(3,0)

= 1 and the corresponding sur-

face is |cos(fni), shown in Fig. 10.1(1). This is a stack, in the horizontal

direction, of four cosine waveforms with frequency index one.

Figure 10.1(o) shows X(l,3) =

1,X(3,1)

= 1 and the corresponding sur-

face is |cos(|(ni + 3n

2

)), shown in Fig. 10.1(p). This is a stack, in the

horizontal direction, of four cosine waveforms with frequency index one

with a shift of §3n

2

.

Figure 10.1(s) shows X(l, 2) = 1, X(3,2) = 1 and the corresponding surface

is |cos(|(ni + 2n

2

)), shown in Fig. 10.1(t). This is a stack, in the hor-

izontal direction, of four cosine waveforms with frequency index one with

a shift of |2n2- The other sinusoidal surfaces, shown in Fig. 10.1, can be

identified similarly. I

The DFT of z(m,n

2

) = e^

ini+m

"

2

\ni, n

2

=

0,1,...,

TV

- 1, where I

and m are positive integers, is similar to that of the 1-D complex sinusoids.

e

j^(ln

1+

mn,) ^ ^2^ _

j^

_

m)

With — I and —m, we get

e

i^(-(ni-mn

2

) ^ ^2^ _ ^ _ ^ ^ _

(j

y _

m))

The DFT of x(n

u

n

2

) = cos(^(/m +mn

2

) + 6),n

l

,n

2

=

0,1,..

.,N - 1,

where I and m are positive integers, is deduced from the previous result.

27T

cos( —(Zni + mn

2

) + 6) O-

TV

2

—(e^(J(fci - I, fc

2

- m) + e-

j9

<5(fci - (N - I), h - (JV - m)))

200

Two-Dimensional Discrete Fourier Transform

With 0 = 0,

cos(^(ln

1

+

mn

2

))<^^-(d(ki-l,k

2

-m)

+

6{k

1

-(N-l),k

2

-(N-m))).

With0 = -f,

sin(^(Zm+mn

2

))

<S>

^-(-jS(k

1

-l,k

2

-m)+j6{k

1

-{N-l),k

2

-{N-m))).

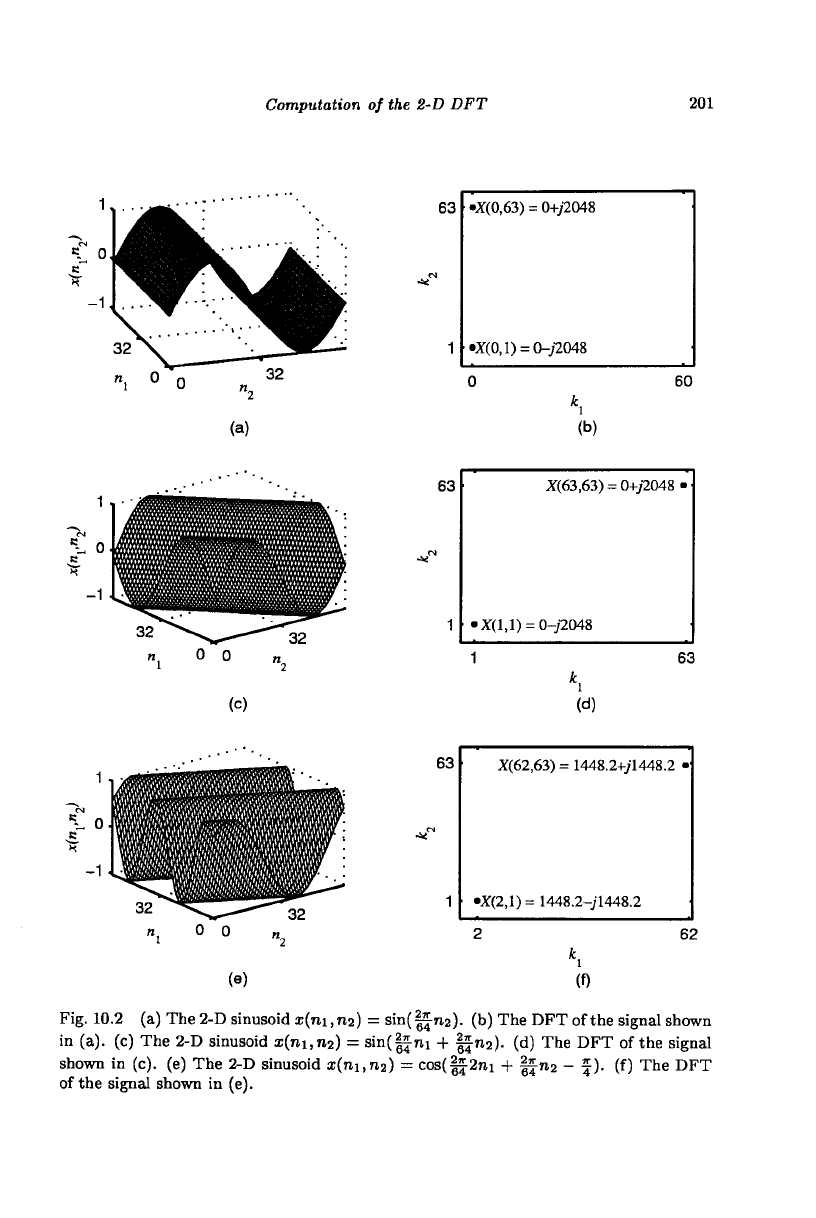
Example 10.2 Consider the 64x64 sinusoidal surface shown in Fig. 10.2(a)

and its DFT shown in Fig. 10.2(b). The coefficients X(0,1) = O-j'2048 and

X(0,63) = 0+J2048 represent a stack, along the ni direction, of 64 shifted

(with zero shift) sine waveforms with frequency index one and amplitude

one,

resulting in the sinusoidal surface, x{n\,n

2

) = sin(|yn

2

). An alternate

view of a sinusoidal surface is of a plane wave with frequency \f{u\ + w

2

)

in the direction 6 = tan

-1

^ to the n\ axis. The sinusoidal surface shown

in Fig. 10.2(a) is a plane wave with frequency |f radians per sample in the

direction 90 degrees to the n\ axis.

Consider the sinusoidal surface shown in Fig. 10.2(c) and its DFT shown

in Fig. 10.2(d). The coefficients X(l,l) = 0 - j'2048 and X(63,63) =

0 + j'2048 represent a stack, in the n

2

direction, of 64 phase shifted sine

waves, sin(|jni), (with |fn

2

radians shift) with frequency index one and

amplitude one, resulting in the sinusoidal surface, x(ni,n

2

) = sin(|jni +

|j7i2).

This sinusoidal surface is a plane wave with frequency

2

^

2

radians

per sample in the direction 45 degrees to the n\ axis.

Consider the sinusoidal surface shown in Fig. 10.2(e) and its DFT shown

in Fig. 10.2(f). The coefficients X(2,1) = 1448.2-J1448.2 and X(62,63) =

1448.2 + j'1448.2 represent a stack, in the n

2

direction, of 64 phase shifted

cosine waves, cos(||2ni), (with (§fn

2

—

j) radians shift) with frequency in-

dex two and amplitude one, resulting in the sinusoidal surface, x(ni,n

2

) =

cos(|^2ni + |f

n

2

— \). This sinusoidal surface is a plane wave with fre-

quency 2sxl radians per sample in the direction tan

-1

\ = 26.565 degrees

to the ni axis. I

10.3 Computation of the 2-D DFT

The direct computation of Eq. (10.1), obviously, has the complexity of

0(AT

4

).

The basis functions, ar

fcllfc2

(ni,n

2

) = e^

(

*

ini+

*

2n2)

,ni,n

2

, h, k

2

=

0,1,...,

N — 1, are separable. Therefore, the 2-DFT can be obtained

by computing the 1-D DFT of each row of the image followed by the com-

putation of the 1-D DFT of each column of the resulting data and vice

Computation of the 2-D DFT

201

« 0

-1

32

", ° 0

32

63 [ »X(0,63) = 0+/2048

1 f»X(0,l) = 0-;2048

60

(a)

(b)

(c)

63

X(63,63) = 0+/2048

<

1 \ •X(l,l) = 0-;2048

1

63

(d)

63 | X(62,63) = 1448.2+/1448.2

1 f •X(2,l)= 1448.2-;1448.2

62

(•)

(f)

Fig. 10.2 (a) The 2-D sinusoid 1(111,712) = sin(||ri2). (b) The DFT of the signal shown

in (a), (c) The 2-D sinusoid 1(711,712) = sin(||ni + §Jri2). (d) The DFT of the signal

shown in (c). (e) The 2-D sinusoid x(ni,n

2

) = cos(|f 2ni + |jn

2

- \). (f) The DFT

of the signal shown in (e).

202

Two-Dimensional Discrete Fourier Transform

versa. This method

is

called the row-column method. Equation (10.1) can

be rewritten

in

two different forms

as

JV-l

X(k

u

k

2

)

=

X^E^'^TO

1

*

1

}^*'

(10.4)

n

2

=0

m=0

JV-l

X(h,k

2

)

= J2{T,

x

^

n

^

W

N

2k2

}

W

N

kl

(10-5)

ni=0 712=0

The expression inside the braces

is

1-D DFT

of

each column

in

Eq. (10.4)

and of each row in Eq. (10.5). The DFT of the

N xN

matrix x(rii,

n

2

)

can

be computed

in

two stages. One way

is to

compute the

1-D

DFT

of

each

column of the matrix

to

get

JV-l

X(h,n

2

)=

^2

x(

ni

,n

2

)W^

k

\

k

lt

Ti2

=

0,l,...,N-l

ni=0

Then, compute the 1-D DFT

of

each row of the resulting matrix

to

get

JV-l

X(h,k

2

)=

J2

x

(

k

uri2)W^

k

\

k

1

,k

2

=

0,l,-..,N-l

712=0

Just

by

decomposing the problem into

2JV

1-D

DFTs,

the

computational

complexity

of

2-D DFT has been reduced

to

0(N

3

).

Example 10.3 Compute

the

2-D DFT

of

the following matrix

of

data

using the row-column method.

n

2

->

2

14 3"

10

2 2

3

10 1

2

0 13.

Compute the IDFT of the transform

to

get back the original image.

Solution

As

the

kernel

is

separable

and

symmetric,

Eq.

(10.1)

can be

written

in

Computation of the 2-D DFT

203

ix form as

" 1 1

1 -3

1 -1

. 1 3

1

-1

1

-1

1 "

3

-1

-3 .

"2143"

10 2 2

3 10 1

.2013.

" 1

1

. 1

1

-3

-1

3

1

-1

1

-1

1

3

-1

-3

Post-multiplying the image matrix by the right kernel matrix is computing

1-D DFT of the rows and we get

1

-3

-1

3

1

-1

1

-1

1 "

3

-1

-3 .

' 10

5

6

-2+J2

-1+J2

3

1+J"3

2

1

0

-2-j2

-1-32

3

1-J3

Pre-multiplying the partially transformed image matrix by the left kernel

matrix is computing 1-D DFT of the columns. The 2-D DFT of the image

is given by

26

5 + jl

4

5-jl

l+j'7

-6+j4

1-J3

-4-jO

4

1-J'l

2

1+jl

1-J'7

-4 + jO

1+J3

-6 - j4

The original image can be obtained by computing row and column 1-D

IDFTs of the transform matrix and vice versa. Note that the kernel matri-

ces of the IDFT are the same as those of the DFT with the difference that

each matrix is to be conjugated. However, similar to the case of computing

the 1-D IDFT, the 2-D IDFT can be obtained using the DFT simply by

swapping the real and imaginary parts in reading the input and writing the

output values. The DFT after swapping the real and imaginary parts is

given by

0 + J26

1+J5

O+j/4

-1+J5

7 + jl

4-j6

-3 + jl

0-J4

0 + j4

-1+jl

0+j2

1+jl

-7 + jl

0-j4

3 + jl

-4 - j6

Sundararaja D. The Discrete Fourier Transform. Theory, Algorithms and Applications

Подождите немного. Документ загружается.