Szilas A.P. Production and transport of oil and gas, Gathering and Transportation
Подождите немного. Документ загружается.


220
7.
PIPELINE TRANSPORTATION
OF
OIL
whence thermal conductivity can
be
calculated
if
@*
is known. In reality, steady heat
flow will take some time to set in and the relationship will become linear after some
time only. This time is, however, short enough (of the order of
10s).
In pipeline-
industry practice, the equation is used in a modified form which takes into account
that the thermal properties ofthe probe differ from those ofthe soil, and contains the
electric current generating the heat flow
-
a directly measurable quantity
-
rather
than the heat flow itself. The depth of penetration of the heat flow into the soil is a
mere
20-
30
mm, and
so
the measurement is to be repeated a number of times at any
location in order to provide a meaningful mean value.
Thermal conductivity in the undisturbed soil is a function
of
instantaneous
humidity, which is affected by the weather. Accordingly,
it
is necessary to take soil
samples simultaneously with the probe measurements, and to determine on these
the humidity of the soil, the bulk density of the dry substance, the clay-to-sand ratio
and the specific heat. In the knowledge
of
these data and using Eqs 7.6-7 and 7.6
-
11,
the thermal conductivity and diffusivity of the soil may
be
extrapolated to any
humidity (Davenport and Conti 1971).
A
longer-term average diffusivity may be
determined recording a full temperature wave on the surface and simultaneously at
a depth of
h
m below ground. Both Eqs 7.6
-
5
and 7.6
-
6 are suitable for calculating
us
in the knowledge of temperature period
t,
and amplitude ratio
AT,,/AT,,
and
phase shift
At,.
-
The temperature wave may be recorded over a full year, or over
the duration of a shorter ‘harmonic’ wave.
7.6.2.
Temperature
of
oil
in steady-state
flow,
in buried pipelines
The flow temperature
of oil
injected into a pipeline will usually differ from soil
temperature, the soil being mostly cooler than the oil. Assuming the heat flow
pattern to
be
steady-state in and around the pipeline, the variation
of
axial oil
temperature in the pipe can be determined along the pipeline as follows. Part of the
potential energy
of
oil flowing in the pipeline, transformed into heat, will warm the
oil.
A
relative increase in temperature will result also from the solid components’
separating out of the oil.
Oil
temperature is reduced, on the other hand, by the
transfer
of
heat from the pipeline into the lower-temperature environment.
In calculating the heat generated by friction let us assume the friction gradient
along the pipeline to be constant on an average.
A
pressure-force differential
Apd?n/4
along a length
1
of pipe generates heat in the amount
Q=
Apd?nl/4.
Neglecting the reduction in flow rate due to the increasing density of the cooling
liquid, we have
l=ut
and
4

7.6.
NON-ISOTHERMAL OIL TRANSPORT
22
I
Using this relationship we may write up the heat generated by friction per
unit
of
time over unit distance of flow:
Q
AP
It
1
@*=
-
=
-q[W/m].
7.6-
12
Let us assume that a temperature drop of
1
"C
=
1
K
causes the solidification of
c
kg of solids (to be called paraffin for simplicity) per kg of oil. Let the heat liberated by
the solidification
of
1
kg of paraffin be
K,
in which case a temperature drop of
1
"C
will liberate heat
in
the amount of qpx, W/K
in
a liquid ofgravity
p
flowing at a rate
q
per second;
t'
and
K
are temperature-dependent, but we shall assume their mcan
values to be constant over the temperature range we are concerned with.
Let
k
denote the heat flow per unit
of
time into the soil from a
unit
length of pipe
per
unit temperature difference,
if
the whole difference is
T,
-
(where T, is the axial
temperature of the
oil
in the pipeline, and is the original soil temperature at the
same depth).
k
is the heat transfer coefficient per unit length of pipe, which we
assume to be constant all along the line. The temperature of flowing oil will decrease
by dT, over a length dl. The change in heat content of liquid flowing at the rate
4
under the influence
of
this temperature difference equals the algebraic sum of the
heat generated, on the one hand, and the heat lost to the environment, on the other,
over an infinitesimal length of pipe dl, that is,
qpc
dT,=
@*
dl+EqpK dT,
-
k(T,
-
T,)
dl
7.6-
13
or,
in a different formulation,
Let
qpc
dT,
-
EqpK
dT/=
@*
dl-
kTJ
dl
-I-
kT,
dl
qpc-&qpK=A
and
@*+kT,=B.
Rearranging and writing up the integration, we have
dT,= dl.
B-kT,
s
Solving this equation under the initial conditions
1
=
0,
T,
=
TJ1
,
and resubstituting
the values
of
A
and
B,
the flow temperature at the end of a pipeline of length
1
turns
out
to
be
T,]-T,-- exp
7.6-
14
@*)
k
[
-qfl(CktEK)]
+
?
'
Let
us
point out that oil temperature will vary also radially
in
any cross-section of
the pipeline. In turbulent flow, radial decrease is slight, but
it
may be significant
in
laminar flow.
Figure
7.6
-
4
shows one of the possible combinations
of
flow-velocity
and temperature-distribution profiles after Chernikin
(1958).
Clearly,
in
this case the
axial temperature
T,
of the oil is somewhat higher than the average temperature.
Example
7.6
-
2.
Let the
ID
of
the pipeline be
di
=
0.2
m, and its length
I
=
20
km.
Oil
of
gravity
p=850
kg/m3 flows at a steady rate of
q=
100
m3/h through the

222
7.
PIPELINE TRANSPORTATION
OF
OIL
pipeline. Injection temperature,
T,
,
=
50
"C; soil temperature,
=
2
"C;
@*
=
7
W/m;
E=
3.0
x
I/T;
C=
1900
J/(kg "C);
2
=
2.3
x
10'
J/kg;
k
=
2
W/(m
T).
Find the tail-end temperature
T,,
of the oil
(i)
assuming that paraffin deposition
takes place over the entire temperature range
of
flow,
(ii)
assuming that paraffin
deposition is negligible, and
(iii)
neglecting both the effects of paraflin deposition
and friction
loss.
-
V=
0
317m/s
T=
55
60
6570
75
''2
Fig.
7.6
-
4.
Rate-of-flow
.-
I
V=
01
02
03
04
05
06
0.7mls
and temperature traverses
of
oil
Ti-
55
5
OC
flowing in a pipeline,
after
Chernikin
(1958)
(i) By
Eq.
7.6- 14,
T',
=
2
+
(50-
2
-
i)
x
+
~
=
28.6
"C
1'
e~p[-0.0278x850(1900+3.0xlo-'x2.3x10~)
2
2X2x
104
(ii)
Assuming that
E
=
0,
+
-
=23'7"C.
I'
2x2x104
T,,
=
2
+
(50
-
2
-
$)
exp
[
-
0.0278
x
850
x
1900 2
(iii)
Assuming that
E
=
0
and
@*
=
0,
=21.7
"C
1
2x2x104
[
-
00278
x
850
x
1900
Tf2
=
2
+(50-
2)
exp
The heat
of
solidification of paraffin (Chernikin
1958)
is rarely taken into account
in practical calculations. It may, however, be of considerable importance, as
revealed by Example
7.6- 2.
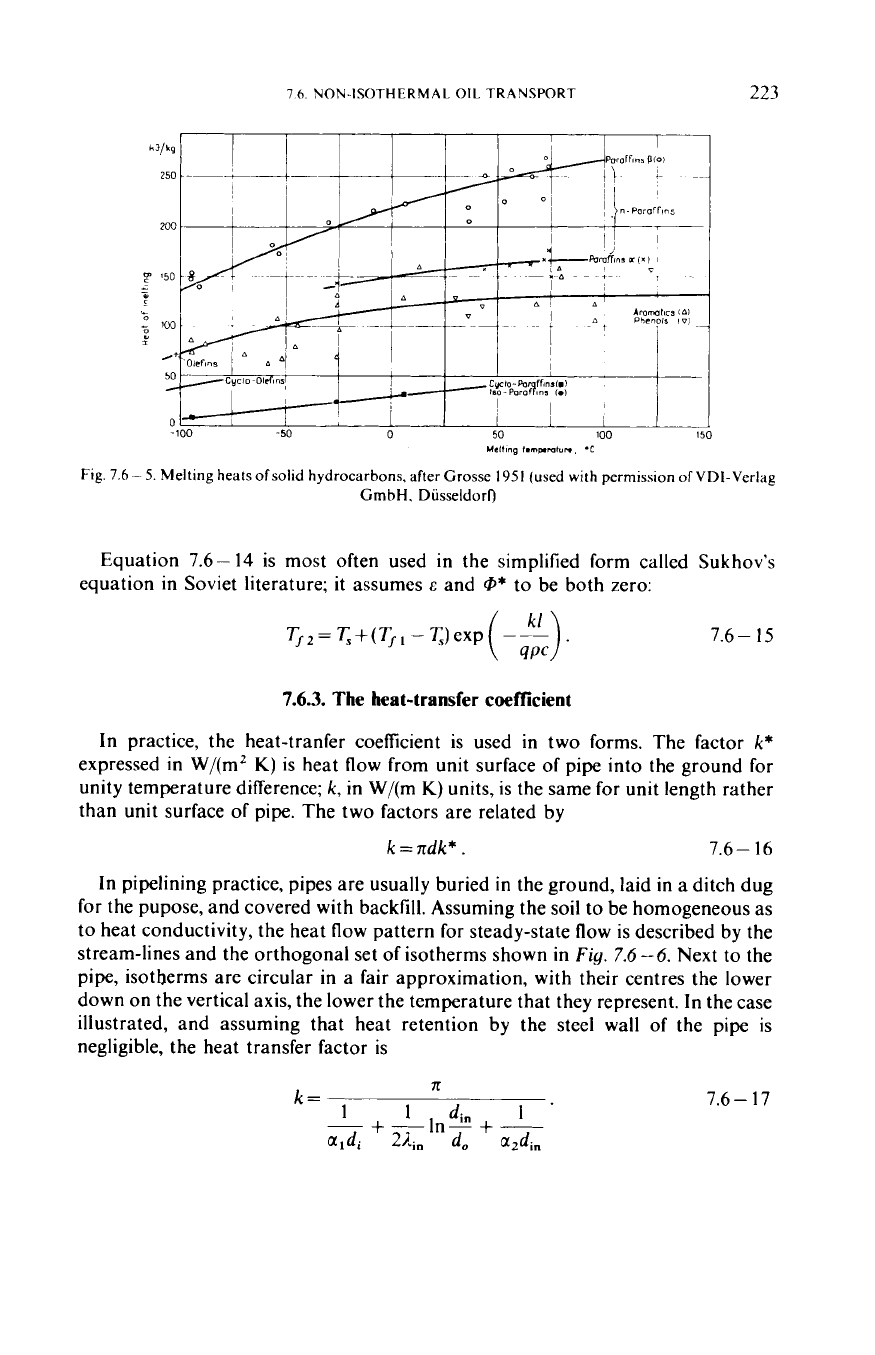
Figure
7.6
-5
is a diagram
of
heats of solidification
v.
melting temperature (after Grosse
1951)
for various paraffins and other high-
molecular-weight hydrocarbons. The latent heat of the components forming
deposits in oil may, according to the data in the Figure, vary rather considerably
depending on solid-phase composition. This enhances the importance
of
knowing
the composition and/or thermal behaviour of the components solidifying within
the
pipeline's temperature range.
As a preliminary indication whether
or
not the heat generated by friction should
be
taken into account, the following rule of thumb may be helpful: heat generated by
100
bars of friction
loss
will raise the tail-end temperature
of
oil flowing
in
the
pipeline by round
4
"C,
irrespective of pipe size and throughput (Haddenhorst
1962).
7
6.
NON-ISOTHERMAL OIL TRAYSPORT
0
-
50
0
50
100
I'
223
Hdhg
1.mpmtun.
.C
Fig.
7.6-
5.
Melting heats ofsolid hydrocarbons. after
Grosse
1951
(used
with
permission
of
VDI-Verlag
GrnbH.
DiisseldorQ
Equation
7.6-
14
is most often used
in
the simplified form called Sukhov's
equation in Soviet literature;
it
assumes
E
and
@*
to be both zero:
T,,
=
T,
+(
T,
,
-
T,)
exp
---
(
3.
7.6-
15
7.6.3.
The heat-transfer
coefficient
In
practice, the heat-tranfer coefficient is used in two forms. The factor
k*
expressed in W/(m2
K)
is heat flow from unit surface of pipe into the ground for
unity
temperature difference;
k,
in W/(m
K)
units, is the same for unit length rather
than unit surface of pipe. The two factors are related by
k
=
ndk*
.
7.6- 16
In pipelining practice, pipes are usually buried in the ground, laid
in
a ditch dug
for the pupose, and covered with backfill. Assuming the soil to be homogeneous as
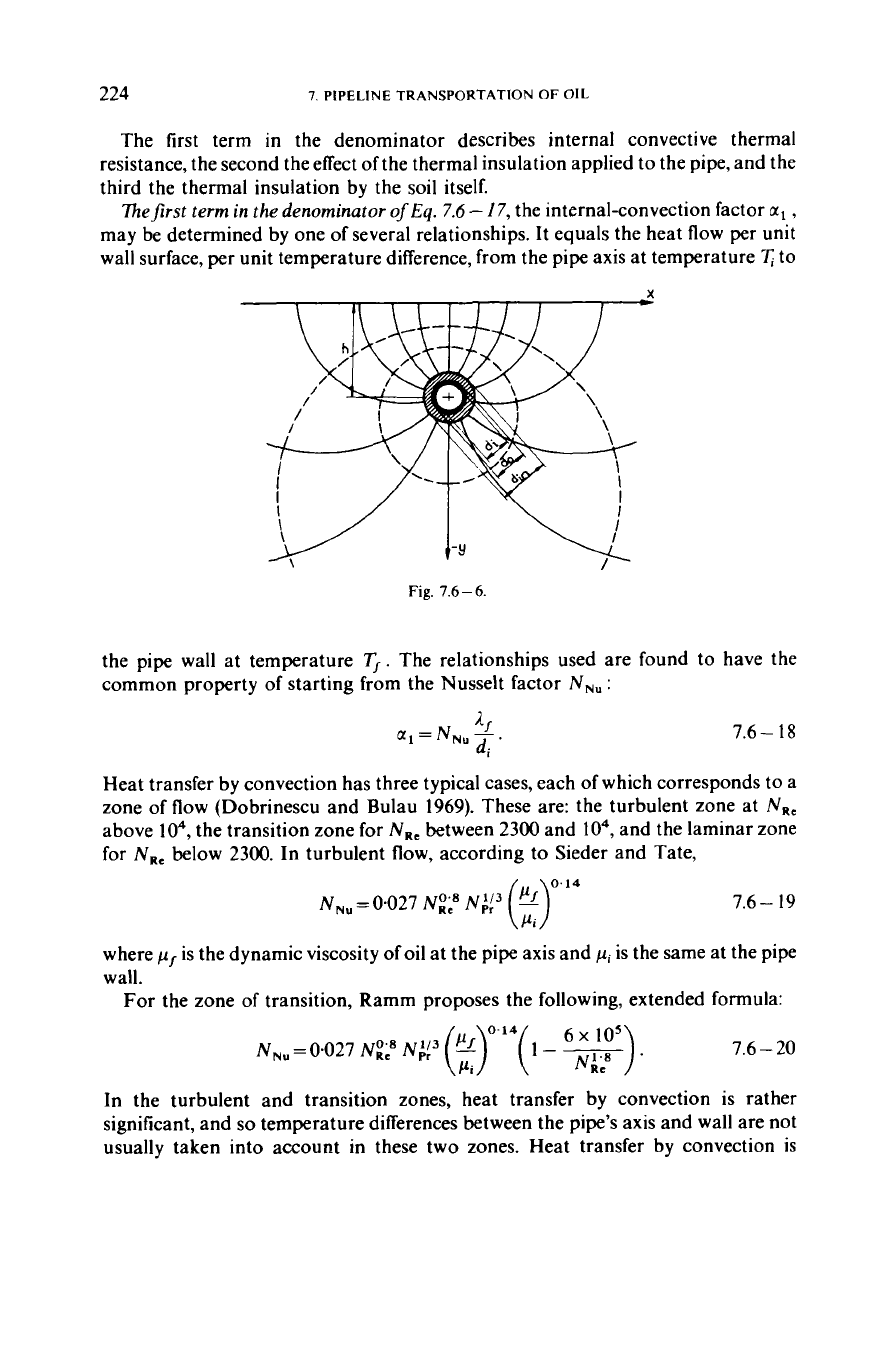
to heat conductivity, the heat flow pattern for steady-state flow is described by the
stream-lines and the orthogonal set of isotherms shown in
Fig.
7.6
-6.
Next to the
pipe, isotherms are circular in a fair approximation, with their centres the lower
down on the vertical axis, the lower the temperature that they represent. In the case
illustrated, and assuming that heat retention by the steel wall of the pipe is
negligible, the heat transfer factor is
n
1 1
din
1
~ +--In-
+
___
a,di 24, do azdin
k=
7.6- 17
224
7.
PIPELINE TRANSPORTATION
OF
OIL
The first term
in
the denominator describes internal convective thermal
resistance, the second the effect of the thermal insulation applied to the pipe, and the
third the thermal insulation by the soil itself.
ntefirst
term
in
the
denominator
ofEq.
7.6
-
17,
the internal-convection factor
a,
,
may be determined by one of several relationships. It equals the heat flow per unit
wall surface, per unit temperature difference, from the pipe axis at temperature to
Fig.
7.6-6.
the pipe wall at temperature
Tf.
The relationships used are found to have the
common property of starting from the Nusselt factor
NNu
:
Jf
di
a1
=
NN,
-.
7.6-
18
Heat transfer by convection has three typical cases, each of which corresponds to a
zone of flow (Dobrinescu and Bulau
1969).
These are: the turbulent zone at
NRe
above
lo",
the transition zone for
N,,
between 2300 and
lo4,
and the laminar zone
for
N,,
below 2300.
In
turbulent flow, according to Sieder and Tate,
7.6-
19
where
p,
is the dynamic viscosity of
oil
at the pipe axis and
pi
is the same at the pipe
wall.
For the zone of transition, Ramm proposes the following, extended formula:
6x
10'
N,,
=
0.027
NE;' N;i3
7.6
-
20
In the turbulent and transition zones, heat transfer by convection is rather
significant, and
so
temperature differences between the pipe's axis and wall are not
usually taken into account in these two zones. Heat transfer by convection is

7
6.
NON-ISOTHERMAL.
OIL
TRANSPORT
225
significantly less in laminar flow; moreover, in liquid undergoing a forced motion.
free convection currents
will
also form, which will modify the velocity profile. This
modification is more significant in vertical than in horizontal flow strings, though.
It
is most expediently characterized in horizontal pipelines by the product
of
the
Prandtl and Grashof numbers (Ford
1955):
7.6-21
For laminar flow,
N,,
v. the product
N,,N,,
can be determined using the Gill-
Russell relationship illustrated by
Fig.
7.6
-
7
(Ford
1955).
If
the abscissa is greater
than
5
x
lo4,
then
N,,
=0.184(N,,Np1)0~32. 7.6
-
22
""
10'
8
6
4
2
10
6
4
2
Fig.
7.6-
7.
Relationship
N,,
=
f(N,,N,,)
for
finding
z,,
according
to
Gill and Russell; after Ford
(1955)
Of
the factors figuring in Eqs
7.6-21
and
7.6-22,
specific heat c and thermal
conductivity
2,
can be calculated using Cragoe's formula transformed into the
SI
system, by Dobrinescu and Bulau
(1
969):
762.5+3.38T
C=
Jz
1
"
=
2583--
6340
p:"
+
5965(pio)'
-
T
.
0134-6.31
x
lO-'T
A/
=
-
Pi0
[J/(kg
K)] 7.6
-
23
[1/K] 7.6-24
[W/(m
K)] 7.6-25
Furthermore
PT=Pn-aT(T-T,)+XpP.
[kg/m3
J
7.6
-
26
The physical state of the oil would, at a first glance, be described in terms of the
average temperature between the head and tail ends of the pipeline section.
IS

226
7
PIPIlLINE
~I
RANSPORTATION
01.
OIL
According to Orlicek and Poll (1959, however, heat transfer depends primarily on
the nature and state of the liquid film adhering to the pipe wall. The correct
procedure would consequently be to determine the physical parameters of the oil at
the mean film temperature.
No
relationship suitable for calculating this temperature
has
so
far been established, however.
For
practice
it
seems best to establish
parameters for the mean wall temperature of the pipeline section examined.
Viscosity depends markedly on temperature, less
so
on pressure
in
the range of oil
transmission in pipelines. The v=f(p,
7)
graphs state results of laboratory
measurements. The temperature-dependence
of
viscosity
in
Newtonian liquids is
best described by Walther's equation
Ig
Ig(106v++)=b+cIg
T
a,
b
and
c
are constants depending on the nature of the oil;
a
ranges from 0.70 to 0.95:
putting
it
equal to
0.8
gives an accuracy sufficient
for
practical purposes. Hence,
Ig
Ig(lO"~+0~8)=b+~Ig
T.
7.6
-
27
This equation implies that
oil
viscosity
v.
temperature will be represented by a
straight line
in
an orthogonal system of coordinates whose abscissa
(7)
axis is
logarithmic and whose ordinate (viscosity) axis is doubly logarithmic. This is the
Walther-Ubbelohde diagram, whose variant conformable to Hungarian standard
MSz-3258-53 is shown as
Fig.
7.6-8.
In principle, two viscosity values
determined at two different temperatures, plotted in this diagram, define a straight
line representing the viscosity v. temperature function. In practice,
it
is indicated to
measure viscosity at three temperatures at least, and to use the straight lines joining
the three points plotted merely as an aid
in
interpolating between plots.
It
should be
ascertained whether or not the oil exhibits anomalous flow behaviour at the lowest
temperature
of
measurement,
or
evaporation losses at the highest.
-
Pressure tends
to increase viscosity somewhat. According to Dobrinescu and Bulau (l969),
dynamic viscosity at pressure
p
is described by
p,,=p,,(O.9789+0~0261
p:')'
OZp.
7.6
-
28
This relationship gives a 13-percent increase
in
the viscosity of a 900 kg/m3 density
oil between atmospheric pressure and
p
=
50
bars.
The second term in the denominator
ojEq.
7.6-
I7
is proportional to the thermal
resistance
of
the heat insulation about the pipe; in addition, to the nature
of
the
insulator matrix, the thermal conductivity of the material as
it
is dependent
primarily on pore volume and pore distribution.
It
is primarily the air
in
the pores
that insulates. The thermal conductivity coefficient ofair at room temperature
(A,,)
is
as low as 0.023 W/(m
K).
If
temperature differences between different points of the
hole wall make the air in the pores form conduction currents, then heat will
flow
through the pores by free convection in addition to conduction. The less the mean
pore size, the less significant is convection. The resultant thermal conductivity of
'series-connected' small pores and the pore walls separating them is less than
it
would
be
for the same overall pore volume
if
the pores were larger.
On
the other

1.6.
NON-ISOTHERMAL
OIL
TRANSPORI
227
Fig.
7.6
-
8.
Walther
-
Ubbelohde grid according
to
Hungarian Standard
MSZ-3258-53
hand, the smaller the pores in a given matrix, the less the compressive strength of the
insulator. Low-strength insulators will be crushed
or
pulverized by comparatively
weak forces. Hence, reducing pore size in a given matrix is limited by the minimum
requirement as
to
compressive strength.
A
material is a good thermal insulator
if
its
conductivity is less than
0.08
W/(m
K);
if
it
contains no substance that corrodes the
pipe;
if
it
is chemically inert vis-a-vis air and water;
if
its compressive strength
exceeds a prescribed minimum;
if
it
keeps its properties over long periods of time;
and
if
it
can be fitted snugly against the pipe wall.
P-C
E
-z
i:
oz
~
5
I
L-P
P-
i
Y
9
\Jl’q
U
,
111
iiy
“I
I
Let us point out that water infiltratcd into the pores
will
considerably impair
insulation, since the thermal conductivity
of
water at room temperature is about
0.58
W/(m
K),
that is, about
25
times that of air. The exclusion of water from the
insulator pores must thercforc
be ensured. This
is
achieved partly by choosing
insulators with closed, unconnected pores, and partly by providing a waterproof
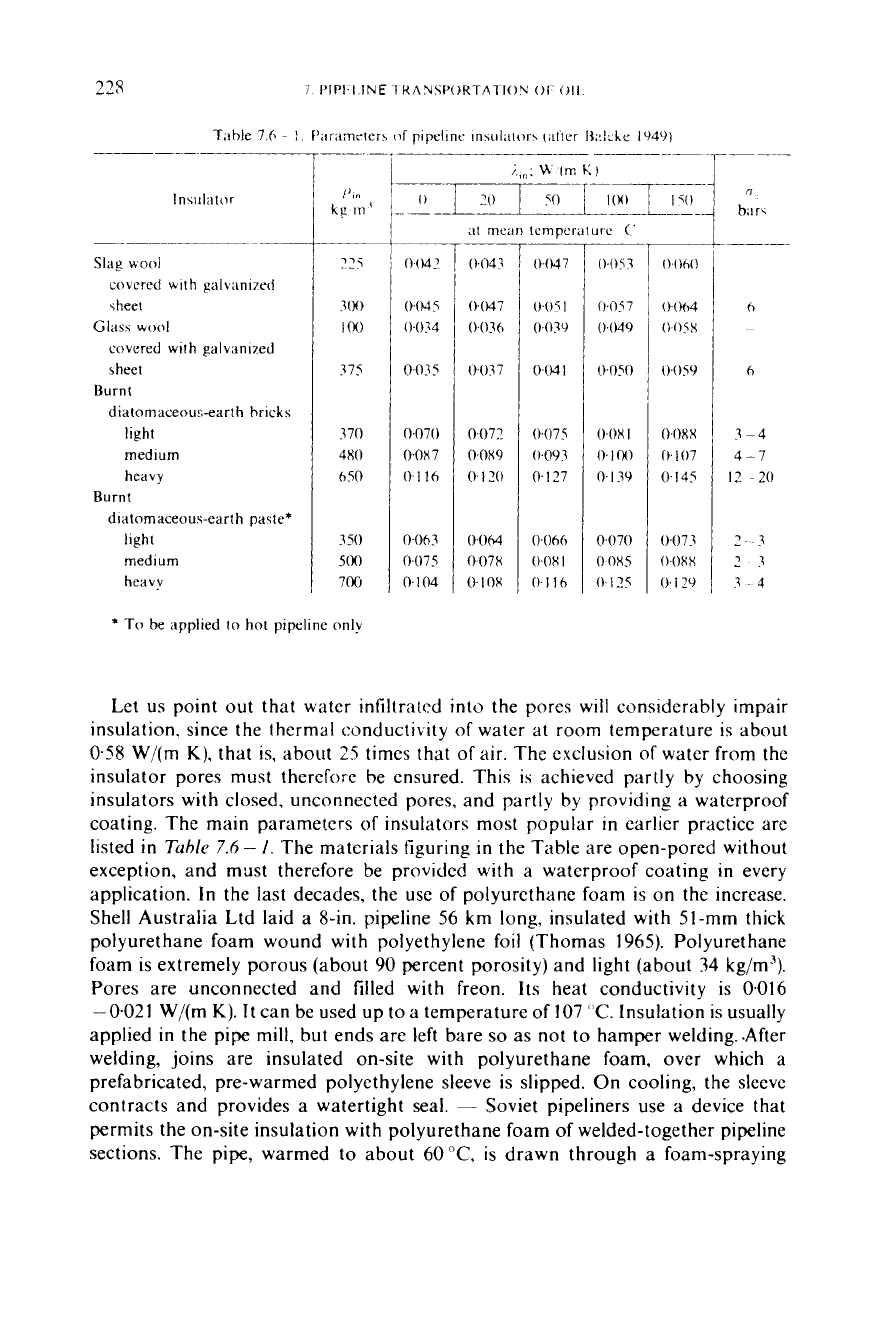
coating. The main parameters
of
insulators most popular
in
earlicr practice are
listed
in
Rihle
7.6
-
I.
The materials figuring
in
the Table are open-pored without
exception, and must therefore be provided
with
a waterproof coating
in
every
application. In the last decades, the use of polyurethane foam is
on
the increase.
Shell Australia Ltd laid a 8-in. pipeline
56
km long, insulated
with
51-mm
thick
polyurethane foam wound with polyethylene
foil
(Thomas
1965).
Polyurethane
foam is extremely porous (about
90
percent porosity) and light (about 34 kg/m').
Pores are unconnected and filled
with
freon. Its heat conductivity is
0.016
-0.021
W/(m
K).
It
can be used up
to
a temperature of 107
"C.
Insulation is usually
applied
in
the pipe mill, but ends are left bare
so
as
not
to
hamper welding..After
welding, joins are insulated on-site
with
polyurethane foam, over which
a
prefabricated, pre-warmed polyethylene sleeve is slipped.
On
cooling, the sleeve
contracts and provides
a
watertight seal.
-
Soviet pipeliners use a device that
permits the on-site insulation with polyurethane foam
of
welded-together pipeline
sections. The pipe, warmed
to
about
60°C
is drawn through a foam-spraying

7 h
NON
1\01
HI
RMAL
011
TR4U\I’OKT
229
chamber. Correct size
is
ensured
by
a
tenlpiate fixed on the chamber wall (Zeinalov
et
ul.
1965).
High-grade heat insu!ation
is
cxpensivc;
it
costs
approximately
as
much
again
3s
the pipelinc itself (Gautrcr
1970)
11ic
(hid
fc’rm
;17
the
dcriomiriutor.
(!/‘E4.
7.6
-
/7describes the thermal resistrincc
of
soil
hurrounding
the
pipeline. Assuming thc original undisturbed tcmperuturc
of
thc
soil
at
pipcline depth
:o
bt:
‘<.
and the ground-surface tcmpcraturc to
be
equal
to
this value,
it
ciin
be
shown that
7.6
-
79
The approxim
;1
t‘
Ion
x2=
4h
di,,
In
-
din
7.6
~
30
will
be
the better, the greater is
h/d,,
.
In most practical cases, that is. at about
h/di,
2
2.
the two formulae
will
furnish closely agreeing results;
din
denotes the
OD
of
thc
pipeline as installed. together
with
insulation and coatings. In the absence of such,
d,,=d,,,
the
OD
of the pipe. Determining the heat conductivity of the soil was
discussed
in
Section 7.6.1,
~~~
In
determining the hcat transfer factor
k
valid when the
pipeline
is
operative, one should keep in mind that the porosity
of
the backfill
is
greater than that of the undisturbed soil, and that its thermal conductivity
is
consequently lower.
A
procedure accounting for this circumstance has been devised
by Ford,
Ells
and Russell (Davenport and Conti 1971). The backfill
will
compact
with
time, and the effcctivc heat-transfer factor
will
slightly increase
in
consequence.
The heat transfer factor is affected by the wind, the plant cover, snow
if
any,
soil
moisture and the state of aggregation of water. Under a temperate climate, soil frost
will
rarely enter into consideration, but
in
permafrost regions
it
may play an
important role. The way wind increases
k,
or the plant
or
snow cover decrease
it,
are
too little known as yet to be evaluated in quantitative terms. The influence of soil
moisture
is
known, however
(it
was discussed
in
Section 7.6.1).
It
is accordingly to
be
expected that the heat transfer factor will vary over the year as a function of
soil
moisture, influenced in its
turn
by
the weather.
Figure
7.6
-
9
is a plot of
k*
factors
measured over three years along threc sections of the Friendship pipeline.
It
is seen
that the factor
is
lowest
in
June,
July
and August, the hot dry months of a Northern
hemisphere continental climate.
If
the heat transfer factor
k
is
to be determined by calculation, and flow is laminar,
then the computation of
s(,
requires the knowledge ofthe inside wall temperature
71,
too
(cf. Eq. 7.6
-
21).
Under steady conditions, heat flow from a one-metre pipeline
section into the soil is
27r4,,(
T,
-
T,,)
In
~~
@*
=
k(
T,
-
T,)
=
a,d,n(
T,
-
7;)
=
=
a2di,,n(7;,
-
T,)
.
7.6-31
d,
n
do
