Tan S.T. Finite Mathematics for the Managerial, Life, and Social Sciences
Подождите немного. Документ загружается.


272 3 MATHEMATICS OF FINANCE272 5 MATHEMATICS OF FINANCE
63. E
FFECTIVE
R
ATE OF
I
NTEREST
Suppose an initial investment
of $P grows to an accumulated amount of $A in t yr. Show
that the effective rate (annual effective yield) is
r
eff
(A/P)
1/t
1
Use the formula given in Exercise 63 to solve Exercises
64–68.
64. E
FFECTIVE
R
ATE OF
I
NTEREST
Martha invested $40,000 in a
boutique 5 yr ago. Her investment is worth $70,000 today.
What is the effective rate (annual effective yield) of her
investment?
65. H
OUSING
A
PPRECIATION
Georgia purchased a house in Janu-
ary, 2000 for $200,000. In January 2006 she sold the house
and made a net profit of $56,000. Find the effective annual
rate of return on her investment over the 6-yr period.
66. C
OMMON
S
TOCK
T
RANSACTION
Steven purchased 1000
shares of a certain stock for $25,250 (including commis-
sions). He sold the shares 2 yr later and received $32,100
after deducting commissions. Find the effective annual rate
of return on his investment over the 2-yr period.
67. Z
ERO
C
OUPON
B
ONDS
Nina purchased a zero coupon bond
for $6724.53. The bond matures in 7 yr and has a face
value of $10,000. Find the effective annual rate of interest
for the bond.
Hint: Assume that the purchase price of the bond is the initial
investment and that the face value of the bond is the accumulated
amount.
68. M
ONEY
M
ARKET
M
UTUAL
F
UNDS
Carlos invested $5000 in
a money market mutual fund that pays interest on a daily
basis. The balance in his account at the end of 8 mo
(245 days) was $5170.42. Find the effective rate at which
Carlos’s account earned interest over this period (assume a
365-day year).
In Exercises 69–72, determine whether the statement is
true or false. If it is true, explain why it is true. If it is
false, give an example to show why it is false.
69. When simple interest is used, the accumulated amount is a
linear function of t.
70. If interest is compounded annually, then the accumulated
amount after t yr is the same as the accumulated amount
under simple interest over t yr.
71. If interest is compounded annually, then the effective rate
is the same as the nominal rate.
72. Susan’s salary increased from $50,000/year to $60,000/year
over a 4-yr period. Therefore, Susan received annual in-
creases of 5% over that period.
(Optional) In Exercises 73–80, use logarithms to solve
each problem.
73. How long will it take $5000 to grow to $6500 if the invest-
ment earns interest at the rate of 12%/year compounded
monthly?
74. How long will it take $12,000 to grow to $15,000 if the
investment earns interest at the rate of 8%/year com-
pounded monthly?
75. How long will it take an investment of $2000 to double if
the investment earns interest at the rate of 9%/year com-
pounded monthly?
76. How long will it take an investment of $5000 to triple if the
investment earns interest at the rate of 8%/year com-
pounded daily?
77. Find the interest rate needed for an investment of $5000 to
grow to an amount of $6000 in 3 yr if interest is com-
pounded continuously.
78. Find the interest rate needed for an investment of $4000 to
double in 5 yr if interest is compounded continuously.
79. How long will it take an investment of $6000 to grow to
$7000 if the investment earns interest at the rate of %
compounded continuously?
80. How long will it take an investment of $8000 to double if
the investment earns interest at the rate of 8% compounded
continuously?
7
1
2
1. Using Equation (7) with A 20,000, r 0.12, and m
12 so that i and n (3)(12) 36, we find the
required present value to be
or $13,978.50
2. The accumulated amount of Paul’s current investment is
found by using Equation (3) with P 100,000, r 0.106,
and m 365. Thus, i and n 365, so the required
accumulated amount is given by
0.106
365
P 20,000 a1
0.12
12
b
36
⬇ 13,978.50
0.12
12
5.1 Solutions to Self-Check Exercises
or $111,180.48. Next, we compute the accumulated amount
of Paul’s reinvestment. Now using (3) with P 100,000,
r 0.092, and m 365 so that i and n 365, we find
the required accumulated amount in this case to be
or $109,635.21. Therefore, Paul can expect to experience a
net decrease in yearly income of
111,180.48 109,635.21,
or $1545.27.
A 100,000 a1
0.092
365
b
365
0.092
365
A 100,000 a1
0.106
365
b
365
⬇ 111,180.48
87533_05_ch5_p257-312 1/30/08 9:55 AM Page 272

Finding the Accumulated Amount of an Investment,
the Effective Rate of Interest, and the Present Value
of an Investment
Graphing Utility
Some graphing utilities have built-in routines for solving problems involving the
mathematics of finance. For example, the TI-83/84
TVM SOLVER
function incorporates
several functions that can be used to solve the problems that are encountered in Sec-
tions 5.1–5.3. To access the
TVM SOLVER
on the TI-83 press , press ,
and then select . To access the TVM Solver on the TI-83 plus and the
TI-84, press , press , and then select . Step-by-step
procedures for using these functions can be found on our Companion Website.
EXAMPLE 1
Finding the Accumulated Amount of an Investment Find the
accumulated amount after 10 years if $5000 is invested at a rate of 10% per year
compounded monthly.
Solution
Using the TI-83/84
TVM SOLVER
with the following inputs,
(10)(12)
Recall that an investment is an outflow.
The number of payments each year
The number of conversion periods each year
PMT:END BEGIN
we obtain the display shown in Figure T1. We conclude that the required accumu-
lated amount is $13,535.21.
EXAMPLE 2
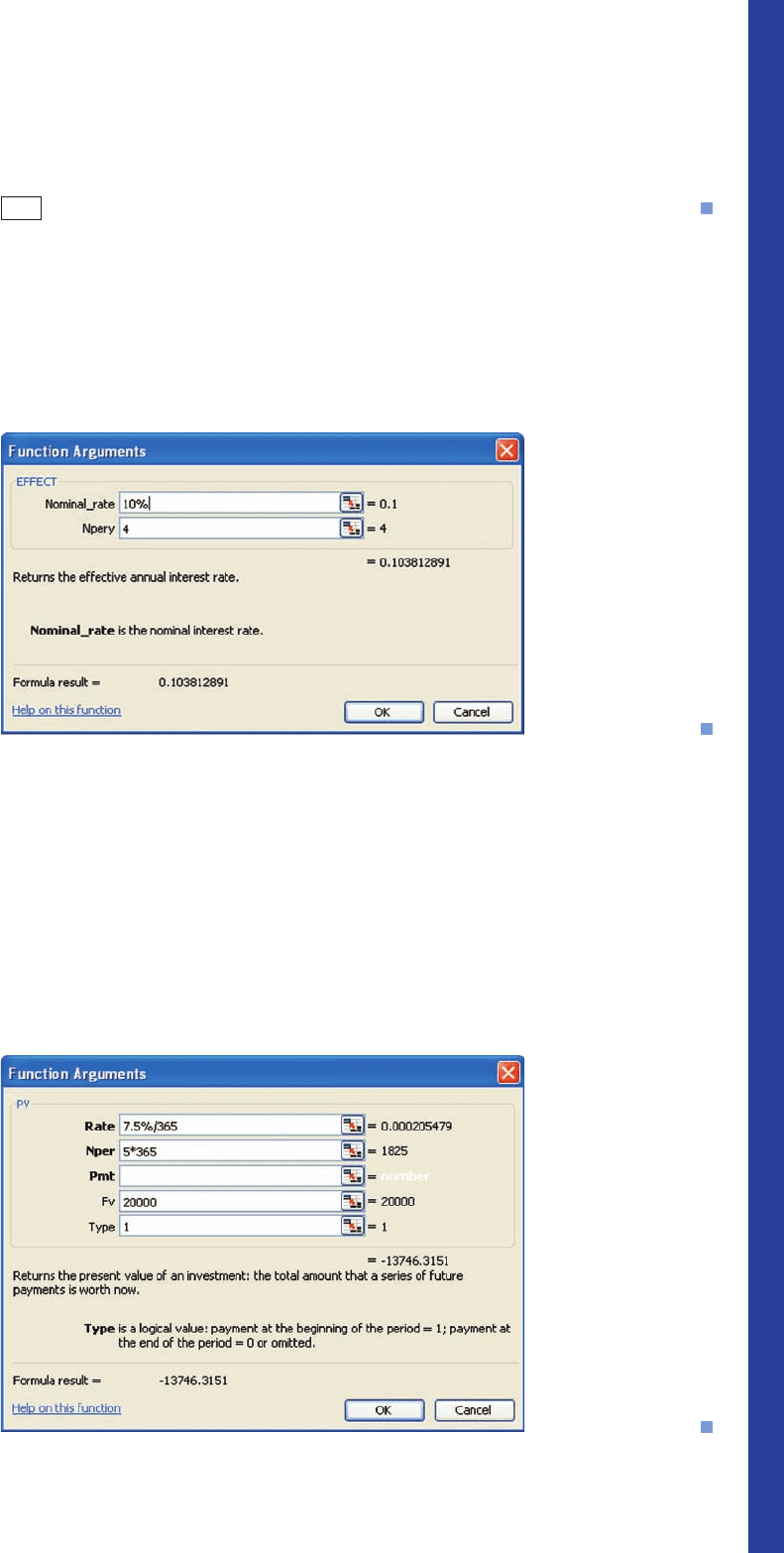
Finding the Effective Rate of Interest Find the effective rate of
interest corresponding to a nominal rate of 10% per year compounded quarterly.
Solution
Here we use the Eff function of the TI-83/84 calculator to obtain the
result shown in Figure T2. The required effective rate is approximately 10.38% per
year.
EXAMPLE 3
Finding the Present Value of an Investment Find the present
value of $20,000 due in 5 years if the interest rate is 7.5% per year compounded
daily.
Solution
Using the TI-83/84
TVM SOLVER
with the following inputs,
(5)(365)
The number of payments each year
The number of conversions each year
PMT:END BEGIN
C/Y 365
P/Y 365
FV 20000
PMT 0
PV 0
I% 7.5
N 1825
C/Y 12
P/Y 12
FV 0
PMT 0
PV 5000
I% 10
N 120
1: TVM Solver1: FinanceAPPS
1: TVM Solver
FINANCE2nd
5.1 COMPOUND INTEREST 273
Eff (10, 4)
10.38128906
FIGURE T2
The TI-83/84 screen showing the effec-
tive rate of interest (Eff)
N = 120
I% = 10
PV = −5000
PMT = 0
FV = 13535.20745
P/Y = 12
C/Y = 12
PMT : END BEGIN
FIGURE T1
The TI-83/84 screen showing the future
value (FV) of an investment
(continued)
USING
TECHNOLOGY
87533_05_ch5_p257-312 1/30/08 9:55 AM Page 273
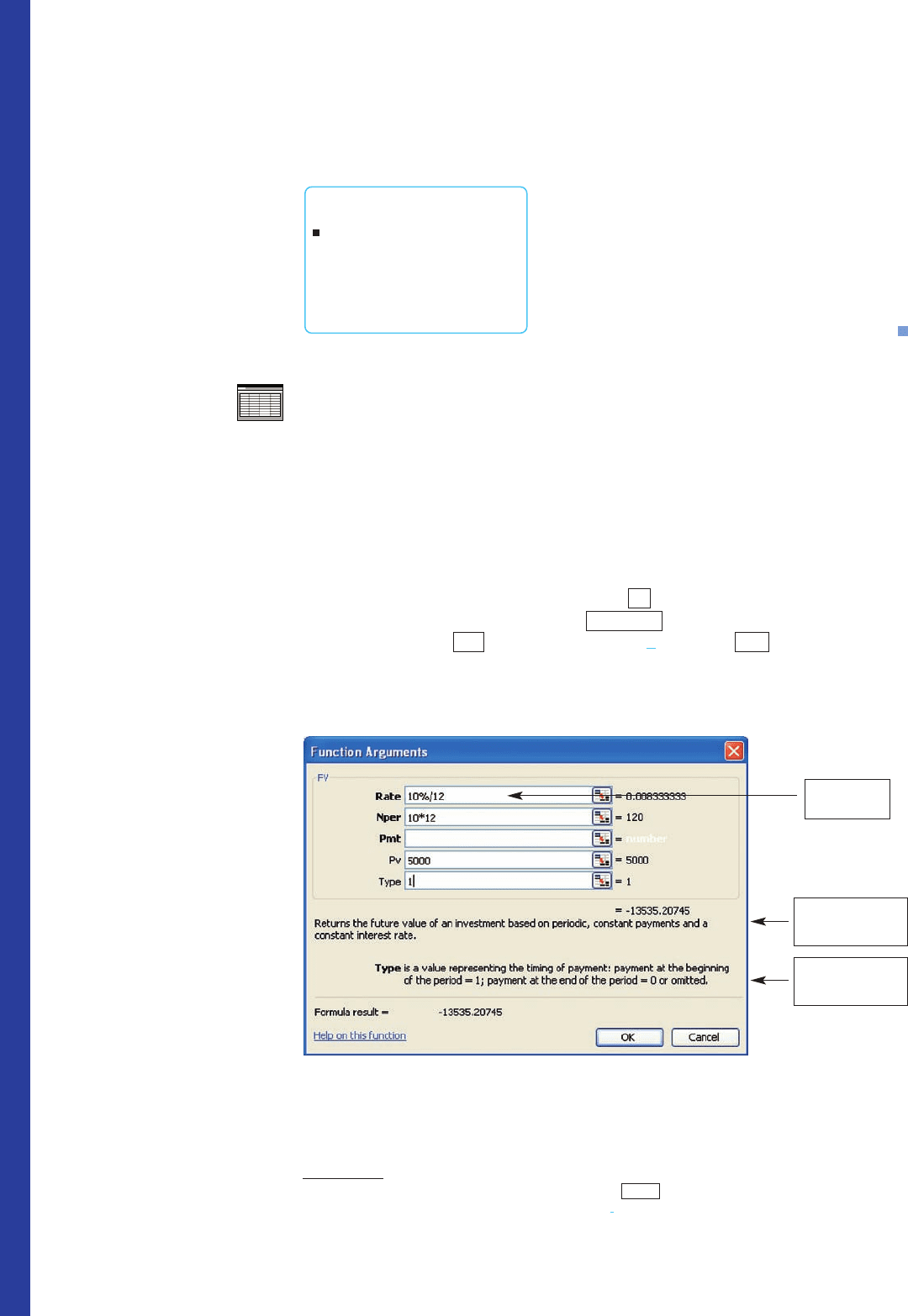
we obtain the display shown in Figure T3. We see that the required present value is
approximately $13,746.32. Note that PV is negative because an investment is an out-
flow (money is paid out).
Excel
Excel has many built-in functions for solving problems involving the mathematics of
finance. Here we illustrate the use of the FV (future value), EFFECT (effective rate),
and the PV (present value) functions to solve problems of the type that we have
encountered in Section 5.1.
EXAMPLE 4
Finding the Accumulated Amount of an Investment Find the
accumulated amount after 10 years if $5000 is invested at a rate of 10% per year
compounded monthly.
Solution
Here we are computing the future value of a lump-sum investment, so
we use the FV (future value) function. Select from the toolbar to obtain the
Insert Function dialog box. Then select from the Or select a category:
list box. Next, select under Select a function
: and click . The Function
Arguments dialog box will appear (see Figure T4). In our example, the mouse cursor
is in the edit box headed by Type, so a definition of that term appears near the bot-
tom of the box. Figure T4 shows the entries for each edit box in our example.
Note that the entry for Nper is given by the total number of periods for which
the investment earns interest. The Pmt box is left blank since no money is added to
the original investment. The Pv entry is 5000. The entry for Type is a 1 because the
OKFV
Financial
f
x
N = 1825
I% = 7.5
PV = −13746.3151
PMT = 0
FV = 20000
P/Y = 365
C/Y = 365
PMT : END BEGIN
274 5 MATHEMATICS OF FINANCE
FIGURE T4
Excel’s dialog box for computing the
future value (FV) of an investment
Edit box
Definition of
function
Definition of
term
Note: Boldfaced words/characters enclosed in a box (for example, ) indicate that an action (click, select, or press) is
required. Words/characters printed blue (for example, Chart sub-t
ype:) indicate words/characters appearing on the screen.
Enter
FIGURE T3
The TI-83/84 screen showing the present
value (PV) of an investment
87533_05_ch5_p257-312 1/30/08 9:55 AM Page 274
lump-sum payment is made at the beginning of the investment period. The answer,
$13,535.21, is shown at the bottom of the dialog box. It is negative because an
investment is considered to be an outflow of money (money is paid out). (Click
and the answer will also appear on your spreadsheet.)
EXAMPLE 5
Finding the Effective Rate of Interest Find the effective rate of
interest corresponding to a nominal rate of 10% per year compounded quarterly.
Solution
Here we use the EFFECT function to compute the effective rate of inter-
est. Accessing this function from the Insert Function dialog box and making the
required entries, we obtain the Function Arguments dialog box shown in Figure T5.
The required effective rate is approximately 10.38% per year.
EXAMPLE 6
Finding the Present Value of an Investment Find the present
value of $20,000 due in 5 years if the interest rate is 7.5% per year compounded
daily.
Solution
We use the PV function to compute the present value of a lump-sum
investment. Accessing this function from the Insert Function dialog box and making
the required entries, we obtain the PV dialog box shown in Figure T6. Once again,
the Pmt edit box is left blank since no additional money is added to the original
investment. The Fv entry is 20000. The answer is negative because an investment is
considered to be an outflow of money (money is paid out). We deduce that the re-
quired amount is $13,746.32.
OK
5.1 COMPOUND INTEREST 275
FIGURE T5
Excel’s dialog box for the effective rate of
interest function (EFFECT)
FIGURE T6
Excel dialog box for the present value
function (PV)
(continued)
87533_05_ch5_p257-312 1/30/08 9:55 AM Page 275

Future Value of an Annuity
An annuity is a sequence of payments made at regular time intervals. The time period
in which these payments are made is called the term of the annuity. Depending on
whether the term is given by a fixed time interval, a time interval that begins at a def-
inite date but extends indefinitely, or one that is not fixed in advance, an annuity is
called an annuity certain, a perpetuity, or a contingent annuity, respectively. In gen-
eral, the payments in an annuity need not be equal, but in many important applications
they are equal. In this section we assume that annuity payments are equal. Examples
of annuities are regular deposits to a savings account, monthly home mortgage pay-
ments, and monthly insurance payments.
Annuities are also classified by payment dates. An annuity in which the payments
are made at the end of each payment period is called an ordinary annuity, whereas
an annuity in which the payments are made at the beginning of each period is called
an annuity due. Furthermore, an annuity in which the payment period coincides with
the interest conversion period is called a simple annuity, whereas an annuity in which
the payment period differs from the interest conversion period is called a complex
annuity.
In this section, we consider ordinary annuities that are certain and simple, with
periodic payments that are equal in size. In other words, we study annuities that are
subject to the following conditions:
1. The terms are given by fixed time intervals.
2. The periodic payments are equal in size.
3. The payments are made at the end of the payment periods.
4. The payment periods coincide with the interest conversion periods.
To find a formula for the accumulated amount S of an annuity, suppose a sum of
$100 is paid into an account at the end of each quarter over a period of 3 years. Fur-
thermore, suppose the account earns interest on the deposit at the rate of 8% per year,
compounded quarterly. Then, the first payment of $100 made at the end of the first
276 5 MATHEMATICS OF FINANCE
1. Find the accumulated amount A if $5000 is invested at the
interest rate of %/year compounded monthly for 3 yr.
2. Find the accumulated amount A if $2850 is invested at the
interest rate of %/year compounded monthly for 4 yr.
3. Find the accumulated amount A if $327.35 is invested at the
interest rate of %/year compounded daily for 7 yr.
4. Find the accumulated amount A if $327.35 is invested at the
interest rate of %/year compounded daily for 8 yr.
5. Find the effective rate corresponding to %/year com-
pounded quarterly.
6. Find the effective rate corresponding to %/year com-
pounded monthly.
10
5
8
8
2
3
6
7
8
5
1
3
6
5
8
5
3
8
7. Find the effective rate corresponding to %/year com-
pounded monthly.
8. Find the effective rate corresponding to %/year com-
pounded quarterly.
9. Find the present value of $38,000 due in 3 yr at %/year
compounded quarterly.
10. Find the present value of $150,000 due in 5 yr at %/year
compounded monthly.
11. Find the present value of $67,456 due in 3 yr at %/year
compounded monthly.
12. Find the present value of $111,000 due in 5 yr at %/year
compounded monthly.
11
5
8
7
7
8
9
3
8
8
1
4
4
3
8
9
3
4
TECHNOLOGY EXERCISES
5.2 Annuities
87533_05_ch5_p257-312 1/30/08 9:55 AM Page 276

quarter earns interest at the rate of 8% per year compounded four times a year (or
8/4 2% per quarter) over the remaining 11 quarters and therefore, by the compound
interest formula, has an accumulated amount of
dollars at the end of the term of the annuity (Figure 2).
The second payment of $100 made at the end of the second quarter earns interest
at the same rate over the remaining 10 quarters and therefore has an accumulated
amount of
dollars at the end of the term of the annuity, and so on. The last payment earns no
interest because it is due at the end of the term. The amount of the annuity is obtained
by adding all the terms in Figure 2. Thus,
S 100 100(1 0.02) 100(1 0.02)
2
100(1 0.02)
11
The sum on the right is the sum of the first n terms of a geometric progression with
first term 100 and common ratio (1 0.02). We show in Section 5.4 that the sum S
can be written in the more compact form
or approximately $1341.21.
To find a general formula for the accumulated amount S of an annuity, suppose a
sum of $R is paid into an account at the end of each period for n periods and that the
account earns interest at the rate of i per period. Then, proceeding as we did with the
numerical example, we obtain
(9)
The expression inside the brackets is commonly denoted by (read “s angle n
at i ”) and is called the compound-amount factor. Extensive tables have been
constructed that give values of for different values of i and n (see, for example,
Table 1 on our Companion Web site). In terms of the compound-amount factor,
(10)S Rs
n
|i
s
n
|i
s
n
|i
R c
11 i2
n
1
i
d
R11 i2
n 1
S R R11 i2 R11 i2
2
⬇ 1341.21
S 100 c
11 0.022
12
1
0.02
d
Quarters
Payments
Periods
0123 910 11 12
$100 $100 $100 $100 $100 $100 $100
Accumulated
amounts
100
100 (1 + 0.02)
100 (1 + 0.02)
2
100 (1 + 0.02)
9
100 (1 + 0.02)
10
100 (1 + 0.02)
11
•
•
•
10011 0.022
10
100 a1
0.08
4
b
11
or
10011 0.022
11
5.2 ANNUITIES 277
FIGURE 2
The sum of the accumulated amounts is
the amount of the annuity.
87533_05_ch5_p257-312 1/30/08 9:55 AM Page 277

The quantity S in Equations (9) and (10) is realizable at some future date and is
accordingly called the future value of an annuity.
EXAMPLE 1
Find the amount of an ordinary annuity consisting of 12 monthly
payments of $100 that earn interest at 12% per year compounded monthly.
Solution
Since i is the interest rate per period and since interest is compounded
monthly in this case, we have . Using Equation (9) with R 100,
n 12, and i 0.01, we have
or $1268.25. The same result is obtained by observing that
1268.25
100112.68252
S 100s
12
|
0.01
⬇ 1268.25
S
100311.012
12
1 4
0.01
i
0.12
12
0.01
278 5 MATHEMATICS OF FINANCE
Use a calculator.
Use Table 1 from the Companion Web site.
Future Value of an Annuity
The future value S of an annuity of n payments of R dollars each, paid at the
end of each investment period into an account that earns interest at the rate of i
per period, is
S R c
11 i2
n
1
i
d
Explore & Discuss
Future Value S of an Annuity Due
1. Consider an annuity satisfying conditions 1, 2, and 4 on page 276 but with condition 3
replaced by the condition that payments are made at the beginning of the payment peri-
ods. By using an argument similar to that used to establish Formula (9), show that the
future value S of an annuity due of n payments of R dollars each, paid at the beginning
of each investment into an account that earns interest at the rate of i per period, is
2. Use the result of part 1 to see how large your nest egg will be at age 65 if you start sav-
ing $4000 annually at age 30, assuming a 10% average annual return; if you start saving
at 35; if you start saving at 40. [Moral of the story: It is never too early to start saving!]
S R11 i2c
11 i 2
n
1
i
d
Exploring with
TECHNOLOGY
Refer to the preceding Explore & Discuss problem.
1. Show that if R 4000 and i 0.1, then S 44,000[(1.1)
n
1]. Using a
graphing utility, plot the graph of f(x) 44,000[(1.1)
x
1], using the view-
ing window [0, 40] [0, 1,200,000].
2. Verify the results of part 1 by evaluating f(35), f (30), and f (25) using the
EVAL
function.
87533_05_ch5_p257-312 1/30/08 9:55 AM Page 278
Present Value of an Annuity
In certain instances, you may want to determine the current value P of a sequence of
equal periodic payments that will be made over a certain period of time. After each
payment is made, the new balance continues to earn interest at some nominal rate. The
amount P is referred to as the present value of an annuity.
To derive a formula for determining the present value P of an annuity, we may
argue as follows. The amount P invested now and earning interest at the rate of i per
period will have an accumulated value of P(1 i )
n
at the end of n periods. But this
must be equal to the future value of the annuity S given by Formula (9). Therefore,
equating the two expressions, we have
Multiplying both sides of this equation by (1 i )
n
gives
(1
i
)
n
(1
i
)
n
1
where the factor (read “a angle n at i”) represents the expression inside the brack-
ets. Extensive tables have also been constructed giving values of for different val-
ues of i and n (see Table 1 on the Companion Web site).
EXAMPLE 2
Find the present value of an ordinary annuity consisting of 24
monthly payments of $100 each and earning interest at 9% per year compounded
monthly.
Solution
Here, R 100, , and n 24, so by Formula (11)
we have
or $2188.91. The same result may be obtained by using Table 1 from the Com-
panion Web site. Thus,
2188.91
100121.88912
P 100a
24
|
0.0075
⬇ 2188.91
P
10031 11.00752
24
4
0.0075
i
r
m
0.09
12
0.0075
a
n
|i
a
n
|i
Ra
n
|i
R c
1 11 i 2
n
i
d
R c
11 i2
n
11 i2
n
11 i 2
n
i
d
P R11 i2
n
c
11 i2
n
1
i
d
P11 i2
n
R c
11 i2
n
1
i
d
5.2 ANNUITIES 279
Present Value of an Annuity
The present value P of an annuity consisting of n payments of R dollars each,
paid at the end of each investment period into an account that earns interest at
the rate of i per period, is
(11)
P R c
1 11 i2
n
i
d
87533_05_ch5_p257-312 1/30/08 9:55 AM Page 279

APPLIED EXAMPLE 3
Saving for a College Education As a savings
program toward Alberto’s college education, his parents decide to deposit
$100 at the end of every month into a bank account paying interest at the rate of
6% per year compounded monthly. If the savings program began when Alberto
was 6 years old, how much money would have accumulated by the time he
turns 18?
Solution
By the time the child turns 18, the parents would have made 144 de-
posits into the account. Thus, n 144. Furthermore, we have R 100, r 0.06,
and m 12, so i 0.005. Using Equation (9), we find that the amount of
money that would have accumulated is given by
or $21,015.
APPLIED EXAMPLE 4
Financing a Car After making a down
payment of $4000 for an automobile, Murphy paid $400 per month for
36 months with interest charged at 12% per year compounded monthly on the
unpaid balance. What was the original cost of the car? What portion of Murphy’s
total car payments went toward interest charges?
Solution
The loan taken up by Murphy is given by the present value of the
annuity
or $12,043. Therefore, the original cost of the automobile is $16,043 ($12,043
plus the $4000 down payment). The interest charges paid by Murphy are given
by (36)(400) 12,043, or $2,357.
One important application of annuities arises in the area of tax planning. During
the 1980s, Congress created many tax-sheltered retirement savings plans, such as
Individual Retirement Accounts (IRAs), Keogh plans, and Simplified Employee
Pension (SEP) plans. These plans are examples of annuities in which the individual is
allowed to make contributions (which are often tax deductible) to an investment ac-
count. The amount of the contribution is limited by congressional legislation. The
taxes on the contributions and/or the interest accumulated in these accounts are
deferred until the money is withdrawn—ideally during retirement, when tax brackets
should be lower. In the interim period, the individual has the benefit of tax-free growth
on his or her investment.
Suppose, for example, you are eligible to make a fully deductible contribution to
an IRA and you are in a marginal tax bracket of 28%. Additionally, suppose you
receive a year-end bonus of $2000 from your employer and have the option of deposit-
ing the $2000 into either an IRA or a regular savings account, where both accounts
earn interest at an effective annual rate of 8% per year. If you choose to invest your
bonus in a regular savings account, you will first have to pay taxes on the $2000, leav-
ing $1440 to invest. At the end of 1 year, you will also have to pay taxes on the inter-
est earned, leaving you with
⬇ 12,043
P
40031 11.012
36
4
0.01
400a
36
|
0.01
⬇ 21,015
S
100311.0052
144
1 4
0.005
0.06
12
280 5 MATHEMATICS OF FINANCE
87533_05_ch5_p257-312 1/30/08 9:55 AM Page 280

1555.20 32.26 1522.94
or $1522.94.
On the other hand, if you put the money into the IRA, the entire sum will earn
interest, and at the end of 1 year you will have (1.08)($2000), or $2160, in your
account. Of course, you will still have to pay taxes on this money when you withdraw
it, but you will have gained the advantage of tax-free growth of the larger principal
over the years. The disadvantage of this option is that if you withdraw the money
before you reach the age of , you will be liable for taxes on both your contributions
and the interest earned, and you will also have to pay a 10% penalty.
Note
In practice, the size of the contributions an individual might make to the vari-
ous retirement plans might vary from year to year. Also, he or she might make the con-
tributions at different payment periods. To simplify our discussion, we will consider
examples in which fixed payments are made at regular intervals.
APPLIED EXAMPLE 5
IRAs Caroline is planning to make a contribu-
tion of $2000 on January 31 of each year into an IRA earning interest at
an effective rate of 9% per year. After she makes her 25th payment on January 31
of the year following her retirement, how much will she have in her IRA?
Solution
The amount of money Caroline will have after her 25th payment into
her account is found by using Equation (9) with R 2000, r 0.09, m 1,
and t 25, so that i 0.09 and n mt 25. The required amount is
given by
or $169,401.79.
After-tax-deferred annuities are another type of investment vehicle that allows an indi-
vidual to build assets for retirement, college funds, or other future needs. The advan-
tage gained in this type of investment is that the tax on the accumulated interest is
deferred to a later date. Note that in this type of investment the contributions them-
selves are not tax deductible. At first glance, the advantage thus gained may seem to
be relatively inconsequential, but its true effect is illustrated by the next example.
APPLIED EXAMPLE 6
Investment Analysis Both Clark and Colby
are salaried individuals, 45 years of age, who are saving for their retirement
20 years from now. Both Clark and Colby are also in the 28% marginal tax
bracket. Clark makes a $1000 contribution annually on December 31 into a sav-
ings account earning an effective rate of 8% per year. At the same time, Colby
makes a $1000 annual payment to an insurance company for an after-tax-deferred
annuity. The annuity also earns interest at an effective rate of 8% per year.
(Assume that both men remain in the same tax bracket throughout this period,
and disregard state income taxes.)
a. Calculate how much each man will have in his investment account at the end
of 20 years.
⬇ 169,401.79
S
2000311.092
25
1 4
0.09
r
m
59
1
2
Accumulated Tax on Net
amount interest amount
5.2 ANNUITIES 281
87533_05_ch5_p257-312 1/30/08 9:55 AM Page 281
