Teodorescu P.P. Mechanical Systems, Classical Models Volume I: Particle Mechanics
Подождите немного. Документ загружается.

MECHANICAL SYSTEMS, CLASSICAL MODELS
90
If a vector
V
′
, equipollent to V (hence
′
=
VV as free vectors), is applied at the
point
P
′
, then we may write (Fig.2.6,b)
()
(
)
O
OP OP PP OP PP
′′′ ′′ ′′′
=×= + ×=×+×
MV V V V V
OP PP
′
=
×+ ×
VV,
hence
()
()
OO
PP
′′
=
+×
MV MV V;
(2.2.3)
the variation of the moment of a bound vector with respect to a given pole, by a change
of the point of application of the vector is thus emphasized. The moment
O
M remains
invariant by a change of the point of application of the vector
V if PP
′
×=
V0; this
condition holds if
=V0 or PP
′
=
0 (trivial cases) or if P
′
belongs to the support of
the vector
V . It results that the above given definition of the moment of a bound vector
with respect to a pole remains valid also in the case of a sliding vector, because we can
thus take an arbitrary point of application of the latter vector on its support.
Let be a pole
O
′
, another one than the pole O . We can write (Fig.2.6,c)
()
(
)
O
OP OO OP OO OP
′
′′ ′
=×= +×=×+×
MV V V V V,
hence
() ()
O
O
OO
′
′
=
+×
MV MV V;
(2.2.4)
this relation shows the variation of the moment of a bound vector by a change of the
pole with respect to which it is taken. The moment
()MV remains invariant if we have
OO
′
×=
V0; this condition is fulfilled if
=
V0 or OO
′
=
0 (trivial cases) or if the
vectors
OO
′
and V are collinear. Hence, the moment ()MV remains invariant if the
pole with respect to which it is calculated is moving along an axis parallel to the support
of the vector
V .
Let
V be the resultant of n bound vectors
i
V , 1,2,...,in
=
, applied at the same
point
P of position vector r with respect to the pole O . Let us perform a vector
product at the left of relation (1.1.5) by
r and take into consideration the distributivity
of the vector product with respect to the vector summation; if we denote
()
ii
O
=×MV rV,
1,2,...,in
=
,
(
)
O
=
×MV rV,
(2.2.5)
then we may write (Fig.2.7,a)
()
(
)
() ()
12
...
n
OO O O
+++ =MV MV MV MV
(2.2.5')
and state

Mechanics of the systems of forces
91
Theorem 2.2.1 (Varignon). The sum of the moments of n bound vectors, having the
same point of application, with respect to a pole, is equal to the moment of their
resultant with respect to the same pole.
Figure 2.7. Theorem of Varignon (a). Case of two vectors V and
−
V , applied at
the same point (b) or at two distinct points on the same support (c).
In the case of two bound vectors V and −V , which are applied at the same point
P and verify the relation (1.1.11), we can write (Fig.2.7,b)
(
)
(
)
OO
+
−=MV M V 0;
(2.2.6)
the result holds also in the case of two sliding vectors having the same support, as well
in the case in which the points of application
1
P and
2
P of two bound vectors are
distinct, but belong to their common support (Fig.2.7,c).
2.1.2 Moment of a vector with respect to an axis
Let be an oriented axis
Δ , of unit vector u , and a bound vector V , applied at a
point
P of position vector r with respect to a pole O arbitrary chosen on the axis. The
moment of the vector
V with respect to the axis Δ is, by definition, the scalar equal to
the projection on the axis of the moment of the vector
V with respect to the point O ,
hence (Fig.2.8,a)
()
(
)
(
)
(
)
pr , ,
O
MM
ΔΔ Δ
≡= =⋅×=VMVurVurV;
(2.2.7)
Figure 2.8. Moment of a vector with respect to a directed axis (a). Variation of
the point of application (b) or of the axis (c).
this definition is correct only if M
Δ
does not depend on the choice of the pole O on
the axis
Δ . Let be another pole O
′
on this axis; a scalar product of the relation (2.2.4)

MECHANICAL SYSTEMS, CLASSICAL MODELS
92
by
u leads to
()
(
)
O
O
′
⋅=⋅uM V uM V, because
(
)
,, 0OO
′
=
uV, hence the
definition is correct. Because the definition given to the moment of a vector with respect
to a pole holds also for a sliding vector, we can state that the definition given for the
moment of a vector with respect to an axis remains valid in the case of a sliding vector
too. In general, the scalar product of the relation (2.2.3) by the unit vector
u leads to
()
()
(
)
,,MM PP
ΔΔ
′′
=+
VVuV,
(2.2.8)
that is to the variation of the moment of a bound vector with respect to an axis by a
change of its point of application (Fig.2.8,b). It results that the moment
M
Δ
remains
invariant if the point of application of the vector
V is moving along an axis parallel to
the axis
Δ (in this case
()
,, 0PP
′
=
uV).
As well, taking an axis
Δ
′
of unit vector
′
=
uu
(equality as free vectors), a scalar
product of the relation (2.2.4) by this unit vector leads to (Fig.2.8,c)
() ()
(
)
,,MM OO
Δ
Δ
′
′
=+
VVuV;
(2.2.9)
hence, the moment
()
M
Δ
V
remains invariant if we can choose two poles
O
and O
′
so that the vectors
OO
′
and V be collinear, hence if the axis Δ with respect to which
this moment is calculated is moving parallel to itself, in a plane parallel to the vector
V .
Taking into account (2.2.1'), we notice that the moments of a vector with respect to
the co-ordinate axes
i
Ox , 1, 2, 3i
=
, are given by
,
i
Ox O i
MM
=
, 1, 2, 3i
=
.
(2.2.10)
Let
i
u , 1, 2, 3i
=
, be the components of the unit vector
u
; taking into account the
relation of definition (2.2.7), we may write the moment of the vector
()
i
VV with
respect to the axis
Δ passing through the point O in the form
()
123
123
123
ij
ijk k
uuu
MxxxuxV
VVV
Δ
==∈V .
(2.2.7')
We will consider a plane
Π normal to the axis Δ at the point O
′
of it and let be the
projection vector
PQ
′′ ′
=
V
of the vector PQ
=
V
on this plane (Fig.2.9); taking into
account the properties of the mixed product, it follows that
()
()
(
)
,, , ,MOPOOOPPPPPQQ
Δ
′
′′ ′ ′ ′ ′
==++++
VuVu V
(
)
,,OP
′
′′
=
uV,
Mechanics of the systems of forces
93
the eight non-written mixed products (obtained taking into account the property of
distributivity of the mixed product with respect to the addition of vectors) vanishing.
Because
u and
()
O
′
′
MV are parallel, we have
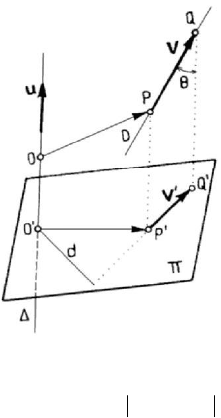
Figure 2.9. Moment of a vector of support D with respect to a directed axis Δ .
()
(
)
(
)
O
MM M
ΔΔ
′
′
′
=
=±VV V,
(2.2.11)
taking the sign + or – as the rotation indicated by the vector
V
′
(hence the vector V )
about the axis
Δ (oriented by the unit vector u ) is positive or negative. Hence, the
modulus of the moment of a vector
V with respect to the axis Δ is equal to the
modulus of the moment of the projection vector of
V on a plane normal to the axis,
with respect to the trace of the axis on the plane. If
D is the support of the vector V ,
we denote by
(
)
,DθΔ= the least angle between the two axes. Let d be the
distance from the point
O
′
to the support of the vector V
′
; we notice that d is just the
length of the common normal to the axes
D and Δ (the least distance between the
points of the two axes). Observing that
sinVV θ
′
=
, taking into account the
expression (2.2.2) of the modulus of the moment of a vector with respect to a pole and
using the formula (2.2.11), we may write
(
)
sinMVd
Δ
θ
=
±V ;
(2.2.11')
one takes the sign + or –, using the criterion enounced above. Hence, the moment of a
vector with respect to an axis vanishes if
0V
=
(trivial case), if 0d
=
(the axes D
and
Δ are concurrent), or if 0θ
=
(the axes D and Δ are parallel); hence, the
moment of a vector with respect to an axis vanishes if and only if the support of the
vector and the axis are coplanar.
2.1.3 The torsor of a sliding vector
Introducing the moment of a sliding vector with respect to a pole, we may give a new
representation for such a vector. Let thus be a sliding vector
V , of components
i
V ,
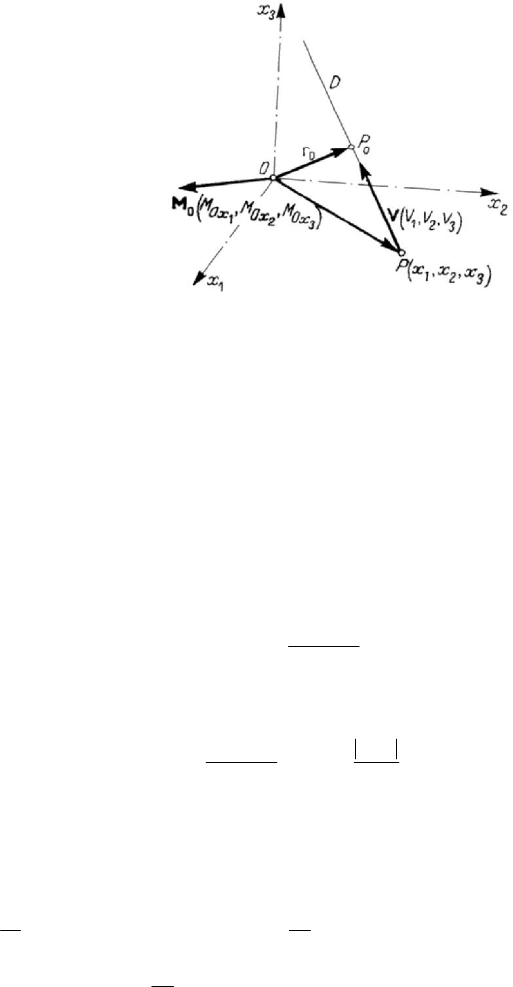
MECHANICAL SYSTEMS, CLASSICAL MODELS
94
1, 2, 3i = , with respect to an orthonormed frame of reference, and let be
O
M
the
moment of this vector with respect to the pole
O (Fig.2.10); we may write the obvious
relation
Figure 2.10. Torsor of a sliding vector with respect to a pole O .
0
i
i
OOx
VM
⋅
==VM .
(2.2.12)
Starting from the expression (2.2.1) of the moment
O
M , we can write the vector
equation
O
×
=−Vr M,
(2.2.13)
where
r is an unknown vector; if we take into account the relation (2.2.12), we may
affirm that this equation, which must determine the support of the sliding vector
V , has
a solution. Using the formula (2.1.54'), the general solution of the equation (2.2.13) can
be written in the form
2
O
V
λ
×
=+
VM
rV
,
(2.2.13')
obtaining thus the equation of the axis
D (the support of the vector V ). We may write
0
2
O
V
×
=
VM
r
,
0
O
r
V
=
M
(2.2.13'')
for
0λ = ; it follows that
(
)
00
P r is the projection of
O
on the axis
D
, because
0
0⋅=rV . Starting from (2.2.13'), we can write the equations of the axis D also in
the form
()()
32 13
22
12 3 23 1
12
11
Ox Ox Ox Ox
Vx VM VM Vx VM VM
VV
−+ = −+
()
21
2
31 2
3
1
Ox Ox
Vx VM VM
V
=−+
.
(2.2.13''')
r
Mechanics of the systems of forces
95
Hence, a sliding vector is characterized by the vectors
V and
O
M
which verify the
relation (2.2.12); such a vector is thus given by two ordered triplets of numbers
(
)
123
123
,,, , ,
Ox Ox Ox
VVV M M M , which verify the relation (2.2.12), hence by five
independent numbers. The six numbers mentioned above are called the co-ordinates of
the sliding vector or Plücker’s co-ordinates.
Since
O
M is the result of the application of an operator on the vector V , the couple
of vectors
{
}
,
O
RM represents the result of the application of another operator on the
same vector
V ; these vectors form the torsor (wrench) of the vector V at the point
(pole)
O ,
()
{
}
,
OO
τ
≡VRM,
(2.2.14)
characterizing entirely the sliding vector. The quantity
O
⋅
RM is called torsor’s scalar
and it vanishes in case of a single sliding vector. Taking into account (2.2.4), we may
write
() ()
{
}
,
O
O
OO
′
′
τ=τ+ ×
VV0R;
(2.2.15)
this relation shows the variation of the torsor of a sliding vector by a change of the pole
with respect to which it is calculated. If the torsor of a sliding vector vanishes at a point,
then it vanishes at any other point; therefore, the necessary and sufficient condition for a
sliding vector to be zero is the vanishing of its torsor at a point.
We also introduce a scalar, called virial, by the relation of definition (Fig.2.10)
()
j
j
OO
xV≡=⋅=VrVVV ;
(2.2.16)
in this case, if we add the number
O
V to the co-ordinates of a sliding vector, then we
obtain the point of application on the support
D . We have thus a new possibility to
represent a bound vector (by six independent numbers).
2.2 Reduction of systems of forces
The forces are modelled with the aid of bound or sliding vectors as they are applied
upon a deformable or non-deformable mechanical system, respectively; a study of the
equivalence of systems of forces (in particular, the equivalence to zero), these ones
being modelled correspondingly, is made. We consider also the systems of free vectors,
because of their importance.
2.2.1 Systems of free vectors
Let
{}
{
}
, 1,2,...,
i
in≡=VV and
{}
{
}
, 1,2,...,
j
jm
′′
≡=VV
be two systems of
free vectors. By definition, we say that the two systems are equivalent if they have the
same resultant
11
nm
ij
ij
==
′
==
∑
∑
RV V;
(2.2.17)
MECHANICAL SYSTEMS, CLASSICAL MODELS
96
in this case, we write
{}
{
}
′
∼VV.
(2.2.18)
The operations of passing from a system of vectors to another system, equivalent to the
first one, are operations of vector addition (composition and decomposition of vectors);
these operations are called elementary operations of equivalence. We consider also the
system of free vectors
{}
{
}
, 1,2,...,
k
kp
′′ ′′
≡
=VV . We mention following properties:
i)
{} {}
∼VV
(reflexivity);
ii)
{}
{} {}
{}
′′
⇔
∼∼VV V V (symmetry);
iii)
{}
{}{}
{
}
{}
{
}
,
′′ ′′ ′′
⇒
∼∼ ∼VVV V VV (transitivity).
Taking into account these properties, we may affirm that the set of elementary
operations of equivalence forms a group.
The simplest system of free vectors equivalent to a given system of free vectors is the
resultant of the latter one. In particular, the resultant of a system of free vectors can be
equal to zero. By definition, we say that a system of free vectors is equivalent to zero
and we may write
{
}
{
}
∼V0
(2.2.19)
if its resultant vanishes
=
R0.
(2.2.19')
A system of free vectors equivalent to zero can be eliminated from computation by
elementary operations of equivalence.
2.2.2 Mathematical modelling of systems of forces
The forces acting upon the mechanical systems have been represented by bound
vectors, and their points of application are the very same points of the system (the
points at which are the particles of a discrete system or the points of a continuous
system). We are thus led to the study of a system of forces modelled by bound vectors.
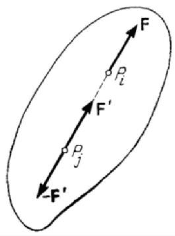
Figure 2.11. Mathematical modelling of a force acting upon a rigid solid.
In the case of a rigid solid, let
i
P be a point of it at which acts a force F (Fig.2.11);
we suppose that at the point
j
P of this solid, on the support of F , is acting a system of
Mechanics of the systems of forces
97
two forces
{
}
{}
,
′′
−
∼FF 0 (system equivalent to zero), considered as bound vectors
and for which holds the relation
′
=
FF, as free vectors. We may write the following
relations of equivalence of the systems of forces
{} {}
{
}
{
}
{
}
{
}
,,
′
′′′′
+− −+
∼∼∼FFFF FFF F,
taking into account the relation
{
}
{}
,
′
−
∼FF 0, because – from a mechanical point of
view – the forces are applied at points which are at an invariable distance between them
(the modelling of the solid as a rigid); by way of consequence, the effect of the force
F
can be replaced by the effect of the force
F
′
. In the case of a rigid solid, the forces will
be thus modelled by sliding vectors. Hence, a force acting upon a rigid solid can be
applied at any point of it, if this point is on the support of the force; this result may be
applied also to a non-deformable discrete system if two or several particles of it are on
the support of the force. Hence, the necessity to study a system of forces modelled by
sliding vectors is put into evidence.
2.2.3 Systems of forces modelled by bound vectors
Let
{}
{}
, 1,2,..., , 1,2,...,
ij i
injn≡= =FF and
{
}
{
, 1,2,..., ,
ik
in
′
′
≡
=FF
}
1,2,...,
i
kn
′
= be two systems of forces modelled by bound vectors; the first index
corresponds to the point
i
P
at which are applied the forces
ij
F and
ik
F
′
, while the
second index individualises the force in the respective system. By definition, we say
that the two systems of forces modelled by bound vectors are equivalent if they have the
same resultant at each point of application
11
ii
nn
iij
ik
jk
′
==
′
==
∑∑
RF F,
1,2,...,in
=
,
(2.2.20)
and this is written in the form
{}
{
}
′
∼FF.
(2.2.21)
The operations of passing from a system of forces to another system of forces,
equivalent to the first one, are operations of vector addition at each point
i
P of the
system; these operations are elementary operations of equivalence in the case of
systems of forces modelled by bound vectors. Let be also the system of forces modelled
by bound vectors
{}
{}
, 1,2,..., , 1,2,...,
i
il
inln
′′ ′′ ′′
≡= =FF . The properties mentioned
in Subsec. 2.2.1 still hold; also in this case, the set of elementary operations of
equivalence forms a group.
The simplest system of forces modelled by bound vectors is formed by the resultants
i
R applied at the points , 1,2,...,
i
Pi n
=
. If
i
=
R0
, 1,2,...,in
=
,
(2.2.22)
then we say, by definition, that the system of forces modelled by bound vectors is
equivalent to zero, and we may write

MECHANICAL SYSTEMS, CLASSICAL MODELS
98
{
}
{
}
∼F0.
(2.2.23)
These results hold also for an arbitrary system of bound vectors. In general, a system of
bound vectors equivalent to zero can be eliminated from computation by elementary
operations of equivalence.
2.2.4 Systems of forces modelled by sliding vectors
Let
{}
{}
, 1,2,...,
i
in≡=FF be a system of forces modelled by sliding vectors.
Besides the operations of vector addition (including composition and decomposition of
vectors), we introduce also the operations of sliding along the support, obtaining thus
the enlarged set of elementary operations of equivalence, which forms a group too.
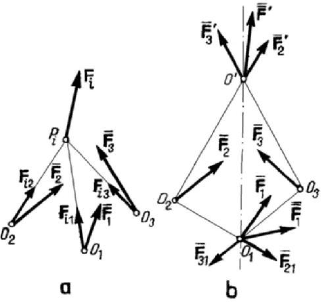
Let us consider three non-collinear points
123
,,,OOO so that the plane Π
determined by them do not contain the supports of the forces
i
F
. We choose the point
of application
i
P of the force
i
F on its support (eventually, we perform a sliding along
this support), so that
i
P Π∉ ; in this case, the force
i
F can be decomposed univocally
along
1
i
PO ,
2
i
PO ,
3
i
PO (Fig.2.12,a) (if the support of the force
i
F is contained in the
plane
Π , then the decomposition remains possible, but it is no more unique). Thus, the
system of forces
{}
F
, modelled by sliding vectors, may be replaced, after sliding along
the supports
1
i
PO ,
2
i
PO ,
3
i
PO , by three subsystems of forces of the same type, applied
at the points
1
O ,
2
O ,
3
O ; summing the forces at these points, we obtain a system of
three forces modelled by sliding vectors
{
}
{
}
123
,,≡FFFF, equivalent to the given
system of forces
{}
F . Because of the arbitrariness in the choice of the points
1
O
,
2
O
,
3
O and
i
P , there exists an infinity of such systems of three forces, which have the
above mentioned property. Let
2
Π and
3
Π be the planes determined by the point
1
O
and the forces
2
F and
3
F , respectively; the intersection of these planes is a straight line
1
OO
′
(the point O
′
is arbitrary on this line) (Fig.2.12,b). We decompose the forces
2
F
and
3
F , along
21
OO and
2
OO
′
, and along
31
OO and
3
OO
′
, in the planes
2
Π and
3
Π ,
respectively; by sliding, these components will be applied at the points
1
O and O
′
,
where we are summing them, together with
1
F . We obtain thus a system of two forces
modelled by sliding vectors
{
}
{
}
1
,
′
≡FFF, equivalent to the system
{}
F , as well as
to the system
{}
F
; the point O
′
is arbitrarily chosen, so that there is an infinity of such
systems of two forces, modelled by sliding vectors.
Let
{}
{}
, 1,2,...,
j
jm
′′
≡=FF
be also a system of forces modelled by sliding
vectors. We say, by definition, that two systems of forces modelled by sliding vectors
are equivalent if, by operations belonging to the enlarged set of elementary equivalence
operations, they can be reduced to the same system of three (or two) forces modelled by
sliding vectors, and we may write a relation of the form (2.2.21). We introduce also the
system of forces
{}
{}
, 1,2,...,
k
kp
′′ ′′
≡=FF
, modelled by sliding vectors; then the
three properties mentioned at Subsec. 2.2.1 hold.
Mechanics of the systems of forces
99
The simplest system of forces modelled by sliding vectors equivalent to a given one
is formed by two forces modelled by sliding vectors. In particular, this system of two
vectors modelled by sliding vectors is equivalent to zero if the two forces have the same
support, the same modulus and opposite directions; in this case, we say that the system
{}
F
of forces modelled by sliding vectors is equivalent to zero, and we write it in the
form (2.2.23). These results hold for any system of sliding vectors. In general, a system
of sliding vectors equivalent to zero can be eliminated from computation by operations
belonging to the enlarged group of elementary operations of equivalence.
Figure 2.12. Systems of forces modelled by sliding vectors. Equivalent systems
of three (a) or two (b) sliding vectors.
2.2.5 Torsor of a system of vectors. The minimal form of the torsor
Because the “torsor” operator appears in connection with any systems of vectors, not
only in connection with systems of forces, we will study this notion for arbitrary
systems of vectors. Let thus
{}
{
}
, 1,2,...,
i
in
≡
=VV be a system of n bound
vectors, applied at the points
i
P
of position vectors
i
r , or of n sliding vectors on
supports passing through these points. We introduce also the resultant
R of the system
of vectors, in the form of a free vector given by (in this relation the vectors
i
V are
considered as free vectors)
1
n
i
i =
=
∑
RV,
(2.2.24)
as well as the resultant moment of the system of vectors, in the form of a bound vector,
applied at the point
O and given by
1
n
ii
O
i =
=×
∑
MrV.
(2.2.24')
We notice that the pair of vectors
{
}
,
O
RM is the result of the application of an
operator
O
τ on a system
{}
V of vectors; this pair of vectors is called, by definition,
the torsor (wrench) of the system of vectors
{
}
V at the pole (point)
O
