Teodorescu P.P. Mechanical Systems, Classical Models Volume I: Particle Mechanics

Подождите немного. Документ загружается.

MECHANICAL SYSTEMS, CLASSICAL MODELS

where

ϕ is an non-dimensional function; applying once again the Π theorem (

,,lmg

are independent dimensional quantities), we obtain

()

ϕθ= .

(1.2.22')

The function

()

ϕθ can be determined only theoretically (by solving the

corresponding mechanical problem) or experimentally. We notice that one can obtain

the formula (1.2.22') also starting from the first formula (1.2.21'). By considerations of

symmetry, one has

()

(

)

ϕθ ϕ θ

− , the function ϕ being an even one; we may thus

admit a development of the form (valid for large oscillations)

()

000

12 3

...cc cϕθ θ θ

+++.

In case of small oscillations, there results

= ,

(1.2.23)

the period

T being thus determined, abstraction making of a multiplicative constant;

the study of this problem leads to

2c π

. Admitting initially that T depends on

,,lgm, but does not depend on

θ , we can write T

cl g m

αβ γ

= ; considerations of

dimensional homogeneity lead to the same formula (1.2.23).

2.3 Similitude

In what follows we make some general considerations and introduce the models of

Froude, Cauchy, Reynolds, Weber etc.; we use thus the geometric, the kinematic and

the dynamic similitude.

2.3.1 General considerations

In many problems of the theory of mechanical systems, the physical phenomenon is

very complex and depends on many parameters, a study of theoretical nature being

extremely difficult; in such cases, it is useful to make an experimental study on

technical models, which reproduce at a reduced scale the considered construction or

element of construction. To do this, we must observe that, generally, any physical

phenomenon is expressed by a system of functional equations, which establish relations

between various physical quantities which appear; the development of the respective

physical phenomenon does not depend on the system of units used.

The models, which will be labelled by index m , will be, at a reduced scale,

constructions similar to the

real ones (original, prototypes), which will be labelled by

index

r . At the basis of a study by modelling, considerations of similitude must be

taken into consideration. The study of physical phenomena on models is made in a

laboratory and is simpler and more economic; but the results thus obtained must be

suitable to the real constructions.

Newtonian model of mechanics

In general, two bodies (the real one and its model) are geometrically similar if their

corresponding lengths are in the same ratio (have the same scale). Analogously to the

geometrical similitude, one can introduce a physical one; we say that two physical

phenomena are similar if it is possible to obtain the characteristics of one from the

characteristics of the other one, on the basis of the respective scales. If

A is an arbitrary

physical quantity, we may write

AkA

(1.2.24)

where

is a coefficient of similitude corresponding to this quantity. An ideal model

must have a perfect similitude (for instance, a

general mechanical similitude) that is the

constant

k must not depend on the particular physical quantity A ; the laws governing

the model are in this case identical to those governing the real object. Practically, such a

model cannot be realized, because one cannot reduce in the same ratio quantities as

lengths, areas, volumes, velocities, accelerations, forces, densities, coefficients of

friction, unit weights etc.; one is thus obliged to use an

incomplete mechanical

similitude

. Taking into account the importance of a quantity or of another one in the

study of a mechanical phenomenon, we may consider a geometric, static, kinematic,

dynamic, thermic similitude etc.; thus, various

similitude criteria are put into evidence.

Newton noticed (1686) that the values of the similitude criteria, homologous to two

similar physical processes, are equal. Federman shows in 1911 that any physical process

can be described with the aid of a functional relation between the respective similitude

criteria.

As V.L. Kirpichev noticed in 1874, two physical processes are similar if and only if

they are qualitatively similar and their homologous similitude criteria have equal values.

We will denote by

,,,λμτχ the similitude coefficients (the respective scales) for

lengths, masses, time and forces, respectively; hence

λ =

μ =

τ =

χ =

(1.2.25)

If for a physical quantity of a special interest we put the condition to have the same

values for the model and for the real object, then there result certain relations between

these coefficients. We put thus in evidence various

laws of similitude (modelling laws),

corresponding to various models.

2.3.2 Geometric, static and kinematic similitude

In the geometric similitude appears only the space and the only basic quantity is the

length. Thus, the scale for lengths will be

ll λ

, the scale for areas

AA λ=

and the scale for volumes

VV λ= .

In the case of

the static similitude, besides lengths one introduces also the forces; in

this case, the independent scales

λ and χ are introduced.

The kinematic similitude introduces the length (scale λ ) and the time (scale τ );

these scales are also independent. One obtains thus: for velocities

vv λτ

−

, for

MECHANICAL SYSTEMS, CLASSICAL MODELS

accelerations

aa λτ

−

= , for angular velocities

ωω τ

−

= , for angular

accelerations

εε τ

−

= etc.

2.3.3 Dynamic similitude. Newton’s similitude law

The dynamic similitude contains the static similitude, as well as the kinematic one;

the ratios between the homologous masses must be also equal, hence the scale

μ of the

masses intervenes. But only three scales are basic, for instance

λ , μ and τ ; taking into

account the basic law (1.1.89) and the accelerations scale, the relation

χλμτ

−

(1.2.26)

called

Bertrand’s characteristic equation, must take place. In this case, the similitude

sets also for the forces. One obtains corresponding scales for various derived quantities

with a dynamical character. Thus, the scale of the unit masses will be

λμ

−

, while the

scale of the unit weights will have the form

λμτ

−

; analogously, one obtains the

scale of the work

λμτ

−

, the scale of the powers

λμτ

−

etc.

To can establish a dynamic similitude between two mechanical systems, one of them

being the real one and the other one the model, it is necessary and sufficient that the

forces acting upon the model do have the same direction as those on the prototype, the

ratio of their moduli being constant and given by the relation (1.2.26); this relation is

called also

Newton’s law of similitude.

For instance, let be

the central motion of a system of particles, the modulus of each

central attractive force being proportional to the mass of the particle and to the distance

at the

nth power with respect to a fixed pole; the ratio χ of the attraction forces

corresponding to the real mechanical system and to its model, respectively, is given by

χλμ

(1.2.27)

Taking into account the relation (1.2.26), we find the condition relation

21n

τλ

−

= ;

(1.2.28)

noting that the particles describe orbits around the attraction centre, we may affirm that

τ is equal to the ratio of the revolution times of these ones. In the particular case of

Newtonian attraction forces (in inverse proportion to the square of distances

2n =− ),

the relation (1.2.28) becomes

τλ=

;

(1.2.28')

hence, the squares of revolution times are proportional to the cubes of the lengths,

corresponding to the third law of Kepler.

Newtonian model of mechanics

2.3.4 Particular models

Newton’s similitude law asks that all the forces which are acting upon the real

mechanical system and upon the model, respectively, be in the ratio

χ given by relation

(1.2.26). Practically, not all the forces can be reduced in the same ratio; hence, from

case to case, one considers only the similitude of those forces which are prevailing in

the phenomenon to study. Thus, we may use various similitude laws (particular

models), which are – in general – of the form

()τϕλ

If we put the condition to obtain the same acceleration for the model and for the real

object (for example, if

the gravity forces are predominant), then we may write

aa λτ

−

, hence

τλ=

;

(1.2.29)

we obtain thus

Froude’s mechanical model. For //

rm rrmm

MM V Vχμ μ μ

()

μμλ=

, in the case in which the model is of the same material as the real

object, we may write

χμλ==.

(1.2.30)

Putting the condition to obtain the same stresses (equal to the ratio between the

forces and the areas of the surfaces upon which they are applied) on the model and on

the real object, we may write

LMT L

rrr r

mmm m

λμτ

−

−−

−

==;

if we use the same material for the model as for the real object, hence if relation (1.2.30)

takes place, then we obtain the law

τλ

(1.2.31)

corresponding to

Cauchy’s elastic model.

If the

internal friction forces have a dominant action (in case of viscous fluids

intervene the

kinematic viscosity coefficient ν ), then we impose the condition

rrr

λτ

−

==;

obtaining thus

Reynold’s hydraulic model for which the relation

τλ=

(1.2.32)

takes place. If the model and the real object are of the same material, the relation

(1.2.30) remains still valid.

The condition that the

superficial tension (equal to the ratio between the force and

the length) measured on the model be equal to that on the real object

MECHANICAL SYSTEMS, CLASSICAL MODELS

LMT L

rrr r

mmm m

μτ

−

leads to

μτ= ;

(1.2.33)

for liquids (the same real object and model) the relation (1.2.30) takes place, so that

τλλ= ,

(1.2.34)

corresponding to

Weber’s model.

Chapter 2

MECHANICS OF THE SYSTEMS OF FORCES

The study of the systems of forces is of a special interest in mechanics because,

applying them upon a body, this one maintains its state of rest or motion or is changing

this state; moreover, the equivalence of the systems of forces represents one of the

objects of study of mechanics, as it was shown in Chap. 1, Subsec. 1.2.3. Taking into

account the vectorial modelling of forces, their algebra is – in fact – a vector algebra.

1. Introductory notions

In what follows we will deal with some applications of the principle of the

parallelogram of forces and of the product of a scalar by a force; one observes thus that

the forces are elements of a vector space. As well, we introduce some important

products of forces, modelled as vectors.

1.1 Decomposition of forces. Bases

The elementary operations which can be effected with forces are the basis for the

study of equivalence of the systems of forces; the decomposition of forces is realized

with the aid of such operations and allows the introduction of the notion of basis of a

system of forces. We notice that all the results which will be given in this section

remain valid for any system of vectors.

1.1.1 Decomposition of forces. Linear dependence

Let us consider the decomposition of a force

F into a sum of n forces

F ,

1,2,...,in= , of given directions. If 3n

and if we admit that the three directions are

non-coplanar, then we obtain a unique decomposition, observing that the force

F is the

diagonal of the parallelepipedon formed with the forces

and

(in general, an

oblique parallelepipedon) (Fig.2.1,a); we thus write

123

++FF F F.

(2.1.1)

3n > , then we may always choose the forces

F , F

,…, F

arbitrarily, and the

decomposition is no more unique; as well, the decomposition is not unique neither for

3n = if the three directions initially chosen are coplanar with the force F . If 2n =

and the chosen directions are coplanar with the force

F , but not collinear, then we

obtain a unique decomposition in the plane (the force

is the diagonal of the

MECHANICAL SYSTEMS, CLASSICAL MODELS

parallelogram formed with

and

) (Fig.2.1,b); if the two directions are collinear

with

F , then the decomposition is no more unique.

Figure 2.1. Decomposition of forces. Three-dimensional (a) and plane (b) case.

Let be

n non-zero forces F

, F

,…, F

. We say that these forces are linear

independent if the relation

11 22

...

λλ λ

++ =FF F0

(2.1.2)

can take place only for zero values of the scalars

λ ,

λ ,…,

λ . From the relation

(2.1.2), it follows

11 22

... 0

FF Fλλ λ+++=

, 1, 2, 3i

(2.1.2')

This linear system in

λ , 1,2,...,jn

, admits only vanishing solutions if and only if

the rank of the matrix of the coefficients of the system is equal to

n ; because this rank

is less or equal to three, it follows that in the three-dimensional space there exist at most

three linear independent forces.

We say that the forces

, F

,…, F

are linear dependent if the relation (2.1.2)

holds, but not all the scalars

,…,

λ vanish. Thus, for

the condition of

linear dependence of the forces

, F

is written in the form

11 22 3 3

λλλ

+=FFF0

;

(2.1.3)

assuming, for instance, that

0λ

≠

, we may express the force F

as follows

123

λμ

+FFF,

(2.1.3')

where

λ , μ are also scalars. It is easy to see that the force F

is contained in the plane

formed by the forces

and

, admitting that these ones are applied in the very same

point. Hence, the necessary and sufficient condition for the three forces to be coplanar

is that they verify the relation (2.1.3), the scalars

λ ,

λ non-vanishing

simultaneously, or the relation (2.1.3'); returning to the system (2.1.2'), the condition is

fulfilled if

Mechanics of the systems of forces

11 21 31

12 22 32

13 23 33

FFF

(2.1.3'')

We notice also that the condition (2.1.3'') is equivalent to

[]

11 12 13

21 22 23

31 32 33

det 0

FFF

FFFF

FFF

= .

(2.1.3''')

In the case

2n = (case considered in Chap. 1, Subsec. 1.1.2), we obtain the

condition of linear dependence

11 22

λλ

=FF0

;

(2.1.4)

this is the necessary and sufficient condition (if the scalars

λ ,

λ do not vanish

simultaneously) for the forces

and

to be collinear. This condition can be written

in the form

FF,

(2.1.4')

where

λ is also a scalar; returning to the system (2.1.2'), the condition becomes

11 12 13

21 22 23

FFF

(2.1.4'')

1.1.2 Basis. Canonical representation of forces

An ordered triplet of linear independent forces

, F

constitutes a basis. In this

case, we can express an arbitrary force

in the form

11 22 33

λλλ

++FF F F

(2.1.5)

where

λ ,

λ are scalars, called the numerical components of the force F in the

given basis. Such a representation can be obtained for an arbitrary vector

V , with the

aid of some vectors

, 1, 2, 3i

, which determine a basis. If the basis’ vectors are

orthogonal one to each other, then the basis is called orthogonal. If the basis’ vectors

are unit vectors, then the basis is called normed. An orthogonal and normed basis is

called orthonormed.

Taking into account the fact that many other mechanical quantities are modelled with

the aid of vectors, we will consider, in what follows, the vectors as abstract

mathematical entities. Let thus be right-handed (or positive) orthonormed bases (if the

vectors are in the order

, V

, then an observer, situated – for instance – along

MECHANICAL SYSTEMS, CLASSICAL MODELS

the vector

, sees the superposition of the vector

onto the vector

, after a

rotation of

/2π in the positive direction, from right to left). More general, a triad of

arbitrary vectors

, V

forms a positive basis, in the given order, if an observer,

situated along the vector

, sees the superposition of the vector V

onto the vector

by a rotation less than π , in the positive direction; the property must be maintained

for a circular permutation of the three vectors.

For a system of Cartesian co-ordinates

Ox , the orthonormed basis’ vectors will be

formed by the unit vectors

i , 1, 2, 3j

, of canonical co-ordinates (1,0,0), (0,1,0),

(0,0,1), respectively, located at O ; in this case, a vector of canonical co-ordinates

V ,

1, 2, 3j = , can be written in the form

(

)

()()()

123 1 2 3

,, 1,0,0 0,1,0 0,0,1

VVV V V V V==++=Vi

;

(2.1.6)

this is the canonical representation of the vector and is unique. In particular, we obtain

the canonical representation of a force

Fi.

(2.1.6')

We notice that the canonical co-ordinates

V ,

V are just the numerical (scalar)

components of the vector,

V i ,

V i being its vector components; because i

, i

are fixed given unit vectors, it is sufficient to use numerical components, which –

for the sake of simplicity – will be called components.

If the vector

V and the unit vectors i

are directed segments, then the numerical

components are numbers; but we mention that, from a dimensional point of view, these

components are not always numbers, their dimensions depending on the physical

dimension of the vector and of the unit vectors of the chosen basis.

In the case of a bound vector

PQ=





, we may write

(

)

() ()QP

xx=−=−= −Vr r QP i,

(2.1.7)

where we have put into evidence the co-ordinates of the origin and of the extremity of

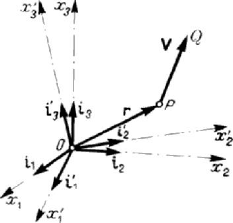
Figure 2.2. A bound vector V in two right-handed systems of co-ordinate axes.

Mechanics of the systems of forces

the vector; this is also the representation of a directed segment. We observe that we may

note a position vector also by the point indicated by it.

Let be a positive orthonormed basis of unit vectors

, hence a right-handed system

of orthogonal co-ordinate axes

Ox , 1, 2, 3j

; let also be a second positive

orthonormed basis of unit vectors

′

, to which corresponds a second right-handed

system of orthogonal Cartesian axes

′

Ox ,

1, 2, 3k

(Fig.2.2). Obviously, we have

kkj

′

ii, 1, 2, 3k

(2.1.8)

where we have introduced the cosines

(

)

cos ,

kj k

′

= ii

, ,1,2,3jk

;

(2.1.9)

analogously, we may write

kj k

′

ii, 1, 2, 3j

(2.1.8')

Let be the position vector

r of a point P ; we obtain, in the two systems of co-

ordinates,

′

=ri i,

(2.1.10)

where

x ,

x , and

′

x ,

′

x ,

′

x , respectively, are the co-ordinates of the point in

each of the two systems. Taking into account (2.1.8) and (2.1.8'), respectively, we find

the relations allowing to pass from a system of co-ordinates to another one

kkj

xxα

′

kj k

xxα

′

, ,1,2,3jk

;

(2.1.11)

these linear transformations are orthogonal.

1.2 Products of vectors

The conditions of orthogonality or of collinearity of two vectors can be expressed

with the aid of their scalar or vector products, respectively; the condition of coplanarity

of three vectors introduces their scalar triple product. One may conceive also a vector

triple product.

1.2.1 Scalar product of two vectors

The scalar product (internal product, dot product) of the (free, bound or sliding)

vectors

and V

is a scalar (which does no more belong to the vector space) defined

by the relation

(

)

12 12 12

cos ,VV⋅=VV VV.

(2.1.12)

In particular, we obtain the projection of a vector

V on a directed axis Δ of unit

vector

u in the form (Fig.2.3)