Teodorescu P.P. Mechanical Systems, Classical Models Volume I: Particle Mechanics

Подождите немного. Документ загружается.

MECHANICAL SYSTEMS, CLASSICAL MODELS

542

In the particular case of the equation (8.2.93), the approximation of second order is

given by

222

cos cos

ττ

τωω

+= −

22 2

00 0

cos cos 3

ττ

ωω ω

⎡

⎛⎞ ⎤

=− −

⎜⎟

⎢

⎥

⎣

⎝⎠ ⎦

wherefrom, taking into account the initial conditions, it results

222

000

() (cos3 cos) sin

τττ τ

ωωω

⎛⎞

=−+−

⎜⎟

⎝⎠

Equating to zero the secular term, we obtain

3/4aω = , so that, in the second

approximation, we have

() 1 cos cos3

32 32

xt a t t

εωεω

ωω

⎡⎛ ⎞ ⎤

=− +

⎜⎟

⎢⎥

⎣⎝ ⎠ ⎦

(8.2.102)

with the pulsation (8.2.94); we find again the period (8.2.94'). The dependence of the

pulsation on the amplitude is thus put into evidence.

The perturbations method may be applied also in case of non-autonomous systems,

the motion of which is modelled by differential equations of the form

(,;) 0xxfxxtωε++ =  ,

(8.2.103)

where the function

is periodic with respect to t and has a known pulsation. By a

phase shifting of the periodic solution with respect to the perturbing force, we may

introduce the phase shift

...δδ εδ εδ=+ + +,

(8.2.104)

the computation procedure being, further, similar to that above.

Among the computation methods which may be applied, we mention also the

graphic methods (the isoclinic lines method, the delta method, the graphic methods for

non-autonomous systems etc.).

Chapter 9

NEWTONIAN THEORY OF UNIVERSAL

ATTRACTION

In the preceding chapter, we have considered the action of an elastic force of

attraction upon a particle, case in which, after Bertrand’s theorem, the orbit is a closed

curve. We will now study the action of forces of Newtonian attraction which, on the

basis of the same theorem, lead to analogous trajectories; we pay a particular attention

to those forces, because they are the most important ones of mechanical nature which

are exerted by a body upon another one. The mathematical modelling of the universal

forces of attraction corresponds to the classical model of mechanics (as it has been

conceived by Newton) and to its gorgeous verification by astronomical observations

(Kepler’s laws). The results thus obtained will be applied to the study of planets’

motions, to the problems of the artificial Earth satellites and of the interplanetary

vehicles, to the motion at the atomic level etc.

1. Newtonian model of universal attraction

After considerations concerning the classical model of universal attraction, a study of

the Newtonian potential is made; the modelling as particles of celestial bodies is just

justified.

1.1 Principle of universal attraction

Starting from Kepler’s laws, considered as laws of experimental nature (obtained by

astronomical observations), we deduce – in what follows – the law of Newtonian

attraction; we can make thus the connection with the gravitational fields.

1.1.1 Law of Newtonian attraction

Starting from the astronomical observations of his predecessors (especially those of

the Dane Tycho Brahe at his observatory on the Ven isle, between Denmark and

Sweden, and then as astronomer at the Imperial Court in Prague), Johann Kepler

enounced three laws which are modelling the motion of planets in the solar system.

Thus, the planets (modelled as particles) describe ellipses with respect to the Sun

(considered to be situated at one of the foci), the motion being governed by the law of

areas; the ratio of the cube of the semi-major axis to the square of the revolution time

is the same for all planets. However, Kepler tried to obtain a synthesis of these laws,

without obtaining a final result (in an Aristotelian conception, he thought that the force

543

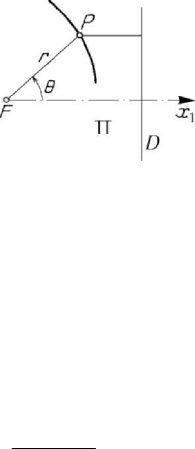
MECHANICAL SYSTEMS, CLASSICAL MODELS

544

is directed along the tangent to the trajectory). But Newton, using Kepler’s laws,

succeeded to set up the mathematical model of classical mechanics, deducing the

expression of the force of universal attraction too; these results (taking into account the

modality to obtain them, they may be considered as deriving from Kepler’s laws, the

latter ones being a mathematical model of mechanics) represent, in fact, the most

important contributions of Newton to the development of mechanics. In

contradistinction to Kepler’s model, the Newtonian one has a general character and may

be applied to all bodies of the real world.

Figure 9.1. Conics.

To can express mathematically Kepler’s laws, it is useful to introduce the equation of

an ellipse and – in general – the equation of a conic in polar co-ordinates. To do this,

we remember that a conic represents the locus of the points

P of a plane Π for which

the ratio of the distances to a fixed point

P Π

∈

(called focus) and to a fixed straight

line

D Π∈ (called directrix), respectively, is constant (the respective constant,

denoted by

e , is called eccentricity) (Fig.9.1); if 01e

≤

≤ , then the conic is an ellipse

(

0e = corresponds to a circle), if 1e

, then it is a parabola, while if 1e > , then it is

a hyperbola. The equation of the conic with respect to the focus

F is written in the

form

1cos

e θ

(9.1.1)

where

0p > is the conic parameter (the semilatus rectum).

Observing that the Sun is at the focus

F , while the planet of mass m is at the point

P , the forces which represent the action of one of the bodies upon the other one are

internal forces in the system formed by the two bodies, modelled as particles. Assuming

that the point

F is fixed (we consider the motion of the planet relative to this point),

the force

F which acts upon the planet is a central force. Because the trajectory of the

planet is an ellipse, it results that the point

F represents a position of stable

equilibrium, the force

F being directed towards this point. The law of areas leads also

to the conclusion that the force

F is a central one. Replacing r given by (9.1.1) in

Binet’s formula (8.1.8), we get

/FmCpr=− ; hence, the magnitude F of the force

is inverse-square to the distance between the Sun and the planet. As we have seen in

Chap. 5, Subsec. 1.1.4,

AΩ



, where the area A is the measure of the surface

described by the radius vector; if that radius describes the whole ellipse, then, by

integrating on the interval

[

]

0,T , where T is the revolution time of the planet (the

time in which the whole ellipse is described), we obtain

2 ab CTπ

, where (6.1.57'')

has been taken into account (the area of the ellipse of semiaxes

a and b is abπ ).

Newtonian theory of universal attraction

545

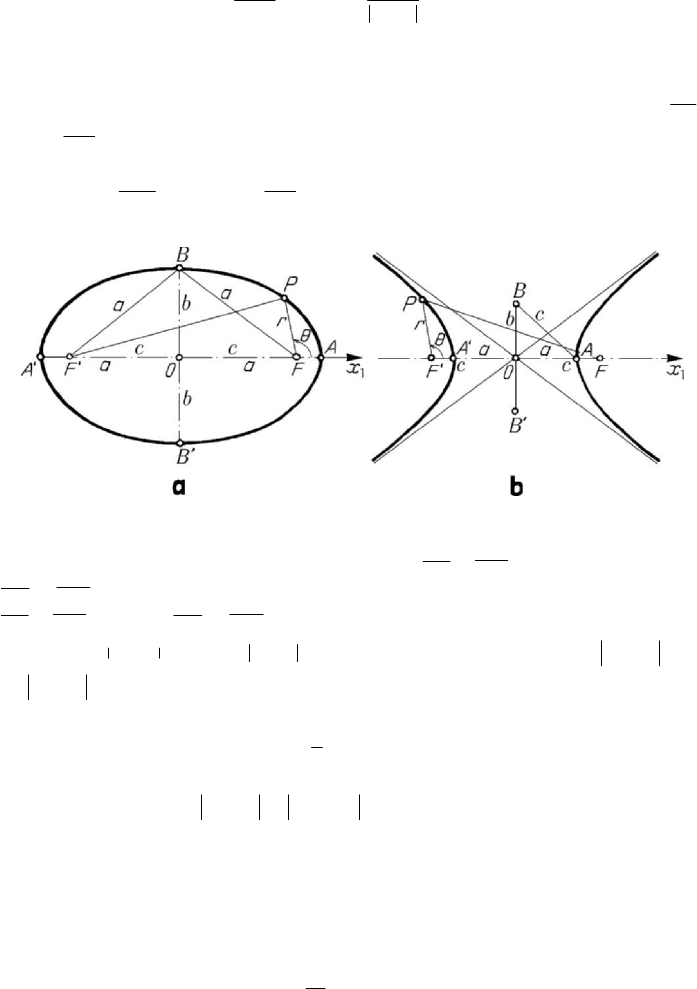
From (9.1.1), one obtains (for

0θ

and θπ

, respectively)

min

max

−

(9.1.1')

corresponding to the apsidal points, called pericentres and apocentres, respectively. It

results

max

min

2rr a±=, as we have to do with an ellipse or a hyperbola, respectively,

0a > being the semi-major axis; in the first case, we have 0r > , so that

min

rFA= ,

max

rFA

′

= (Fig.9.2,a), while in the second case we have

0r ≷

as it corresponds to

the branch of the hyperbola the focus of which is taken as origin or to the other branch,

so that

min

rFA

′′

and

max

rFA

′

= (Fig.9.2,b). We also notice that

Figure 9.2. Conics. Ellipse (a). Hyperbola (b).

the ellipse is the locus of the points for which

2constPF PF a

′

(so that

BF BF a

′

==), while the hyperbola is the locus of the points for which

2PF PF a

′

−=. If 0FO F O c

′

==> is the focal distance to the centre, it results

/(1 )peac+=−, /1peac

−

=+, wherefrom

/1pe e c−=

/1pea−=; for both conics we get thus the eccentricity

(9.1.2)

and the parameter

222

1/pa e a c a=−=− . Observing that

222

acb

± ,

(9.1.2')

where

0b > is the semi-minor axis (the semi-major axis of the conjugate hyperbola, in

case of a hyperbola), we may write

(9.1.2'')

MECHANICAL SYSTEMS, CLASSICAL MODELS

546

In this case,

22222232

/4 / 4 /Cp abpT aTππ==, so that

π=− ;

(9.1.3)

taking into account the third law of Kepler (see Subsec. 2.1.4), there results

μ=− ,

(9.1.3')

where

() 0Mμμ

> , M being the Sun mass ( μ depends only on the Sun, because

it is independent of the particular planet considered). Newton assumed that this

independence is linear, so that

()MfMμ

, the force exerted by the Sun upon the

planet of mass

m , situated at the distance r , being thus given by

=−

(9.1.3'')

and corresponding to the formula (1.1.84'). Indeed, if the action of the Sun upon a

planet

P of mass

m is a force of modulus

mrμ , ()Mμμ

, and if the planet

P acts upon the Sun with a force of modulus

Mrμ

, ()

mμμ

, then,

corresponding to the principle of action and reaction, we may write

mr Mrμμ= , 1,2,...,j = wherefrom

11 22

/ / / ...Mm mμμ μ

==; the

common ratio is just the constant

of universal attraction, which leads to the

expression of the universal (Newtonian) law of attraction. This model of the force of

attraction of the bodies in Universe has been extended by Newton for all the bodies,

immaterial of the magnitudes of their masses, in the form (corresponding to the formula

(1.1.84))

=−

(9.1.4)

where

m and

m are the masses of two bodies situated at the distance r one of the

other (the distance between their centres of mass, the bodies being modelled as

particles). As we have seen in Chap. 1, Subsec. 1.1.12, these forces are conservative.

One obtains thus the universal (Newtonian) law of attraction.

The coefficient

may be obtained experimentally in a particular case and is given,

in the CGS – system, by

6.6732 10

−

=⋅

1/ 3871 cm/g s

≅

⋅ . The first

determination in a laboratory has been made a century later by Cavendish, in 1798, with the

aid of a balance of torsion. The apparatus is formed by a thread

AB suspended at A

and supporting at the end

B a horizontal bar at the ends of which are two small spheres

and

(

BP BP= ) of masses

m and

m , respectively. If we put in the vicinity

of these spheres a fork with two spheres

′

and

′

of masses

′

 and

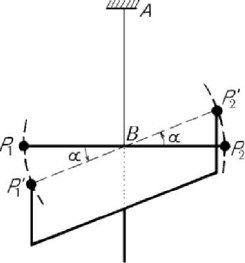
Newtonian theory of universal attraction

547

′

 , respectively (usually,

and

′

), then, due to the forces of

Newtonian attraction which arise, the sphere

P is attracted by the sphere

′

and the

sphere

P is attracted by the sphere

′

; thus, a circular motion of angle α takes place

(Fig.9.3). The thread

AB is subjected to torsion, wherefrom the denomination of the

apparatus. Because the angle

α is proportional to the couple formed by the Newtonian

forces of attraction applied upon the particles

P and

P , one can calculate the

coefficient

Figure 9.3. Balance of torsion.

Building up a mathematical model of universal attraction, in the frame of a classical

model of mechanics, Newton opened a large outlook to the development of science;

among others, this model is the basis of celestial mechanics, where the fundamental

problem is that of

n particles (e.g., The Sun, the Earth and the Moon – the problem of

the three bodies, modelled as particles). Starting from the Newtonian theory of

universal attraction, one could show, only by computation, that the Earth is an oblate

spheroid (it is oblate at the poles), one could discover, only by computation too, new

planets (thus, Leverrier discovered, in 1846, the planet Neptune, and – recently – a

tenth planet has been intuited), one could predict the trajectories of the interplanetary

vehicles (stating thus the basis of the theory of cosmic motions) etc.

In the following section we show that all celestial bodies, considered to be of quasi-

spherical form, may be modelled as particles situated at their centres of mass and

having a mass equal to that of the respective body.

1.1.2 Law of universal gravitation

We have seen in Chap. 1, Subsec. 1.1.12 that the gravity forces, due to the presence

of a gravitational field, may be considered as particular cases of forces of Newtonian

attraction (which, by extension, are called forces of universal gravitation too); one

obtains thus the law of universal gravitation. Hence, it results the remarkable relation

(1.1.85), which links the constant

to the mass

of the Earth, considered as a

sphere of radius

R , and to the gravity acceleration g .

The potential

mM R (m is the mass of a body situated at the distance H from

the Earth surface, along the local vertical) must be replaced by

MECHANICAL SYSTEMS, CLASSICAL MODELS

548

(

)

(

)

mM mM H mM H

ff f

RH R R R R

−

=+≅−

mM mM mM

fHf mgH

=− ≅−,

where we took into account (1.1.85). This potential differs from that known (see

formula (1.1.83)) by the additive constant term

mM R . We notice that in case of the

potential

/( )

mM R H+ the zero level is at infinity, while in case of the potential

mgH− the zero level is at the Earth surface.

The motion of a particle in a gravitational field leads to the equation

mm=ag,

where, due to the equality between the inertial mass and the gravitational one (the

relation (1.1.24)), these ones disappear from computation. In case of a motion in an

electric field

, which acts upon the particle with the force

, where e is the electric

charge, the equation of motion is of the form

aE; (9.1.5)

in this case, the inertial mass does no more disappear, being different from the electric

charge

e .

Let us consider the motion of the Moon around the Earth; a force of attraction of the

form (9.1.3), (9.1.3'), for which

23 2

4/aTμπ= , arises. A particle of mass equal to

unity at the Earth surface is attracted to that one by a force equal to

11/gRμ⋅=⋅ ,

being a constant which depends on the mass of the Earth of radius

R . We obtain thus

the relation

π= ,

(9.1.6)

which allows to calculate the gravity acceleration. The trajectory of the Moon is quasi-

circular, with

60 384 000 kmaR≅≅ ; it results

23 2

460 /gRTπ≅ . Because

6370 kmR ≅ and 2 40 000 kmRπ ≅ , the time of revolution of the Moon being 27

days 7 hours 43 minutes

39 343 60 s=⋅, Newton has obtained

9.8 m/sg ≅ , in a

good concordance with the result previously obtained by Galileo. Taking into account

what was shown above, it results that the ratio of the acceleration

γ of a free fall of the

Moon on the Earth to the gravity acceleration

g is equal to the ratio

(/) 1/60Ra ≅

;

taking

9.81 m/sg = , we get

2.72 10 m/sγ

−

=⋅ , result which corresponds to that

obtained in the study of Moon’s trajectory. Thus, we get a brilliant confirmation for the

coincidence of the two forces (the gravitational attraction and the weight at the Earth

surface).

The relation (1.1.85) allows to determine the mass of the Earth in the form

/MgRf≅ ; observing that

4/3MRπμ= , where μ is the mean unit mass, it

results

Newtonian theory of universal attraction

549

= .

(9.1.6')

We get thus

5.51 g/cmμ = . This density is much greater than that of the superior

spherical strata of the Earth; we may thus conclude that the density is much greater

towards the centre of the Earth.

As we have seen in Chap. 1, Subsec. 2.1.3, the mass can be taken as derived unit,

which is expressed by means of units of length and of time as basic units, so that the

universal constant

becomes equal to unity. We introduce thus the natural hour

(which is approx. equal to 3871 seconds of mean time); this is the unit of time which

must be adopted so that, for an arbitrary unit of length and a unit of mass corresponding

to a cube of di1stillated water at

4C° , equal to unity, to obtain 1

1.2 Theory of Newtonian potential

To justify the modelling of celestial bodies as particles, we introduce – in what

follows – the Newtonian potential and put into evidence some of its properties; we

consider especially the surface and the volume potentials of the homogeneous sphere,

as well as the potential of the spherical stratum. We give some results concerning the

potential of the terrestrial spheroid too.

1.2.1 Newtonian potential

Corresponding to the universal gravitation law, a particle

Q of position vector ξ

and mass

m acts upon a particle P of position vector r and mass equal to unity with a

force of attraction given by

vers grad grad

mfm

QP f U

=− = =

JJG

F , R

−r

(9.1.7)

where the potential (see the formula (1.1.84'))

(9.1.7')

has been introduced (we have neglected an additive constant); thus, the projection of

the force

F on a direction of unit vector n is given by grad /

UfUn

⋅

=∂ ∂n .

In case of several centres of attraction

Q of position vectors

and masses

m ,

1,2,...,jn= , we obtain (in conformity with the principle of the parallelogram of

forces)

grad

U=F ,

∑

R =−r

(9.1.8)

Let be, in general, a mechanical system

S of geometric support Ω , at a finite

distance; the potential of the force of attraction

F exerted by S on the particle P is

given by the Stieltjes integral

MECHANICAL SYSTEMS, CLASSICAL MODELS

550

()

Ω

∫

r , R

−r

(9.1.9)

where ()mm

ξ is a distribution. Introducing the unit mass (1.1.71), (1.1.71''), we

obtain the relation (9.1.8) for a discrete mechanical system of

n particles

Q of

position vectors

ξ and masses

m , 1,2,...,jn

, or

()

() d

∫∫∫

, R

−r

(9.1.8')

in case of a continuous mechanical system of unit mass

() ( )CV Sμ ∈+ξ

(S is the

frontier of the domain of volume

V and verifies conditions of Lyapunov type).

If the continuum is homogeneous, then it results

()

μ=

∫

∫∫

r , R

−r

(9.1.8'')

We obtain thus the general form of the Newtonian potential, that is the volume potential

given by the formula (A.2.86). In case of a two-dimensional mechanical system

S, we

replace the volume integral by a surface one (it results a simple stratum potential of the

form (A.2.87)), using a superficial unit mass; if the mechanical system is plane, then the

integral is a double one. As well, in case of a one-dimensional mechanical system

S we

replace the volume integral by a curvilinear one, introducing a linear unit mass.

One can put in evidence following properties:

()U r is a continuous function in the whole space and vanishes at infinity.

ii)

The derivatives of first order of

()U r (hence, the vector field grad ( )U r too)

are continuous functions in the whole space and vanish at infinity; they are

calculated by differentiation under the integral sign.

iii)

The derivatives of second order of

()U r have jumps by crossing the surface

; in particular, (one can make the connection with the formula (A.2.85))

4 ( ) in the interior of ,

()

0 in the exterior of .

πμ−

⎧

⎪

Δ=

⎨

⎪

⎩

(9.1.10)

iv) The behaviour at infinity of the potential is given by

(

)

() vers

=+ ⋅ +rrρ

O .

(9.1.11)

For the first two properties we assume that

()μ

is a bounded and integrable on V

function, while for the property iii) we consider that

()μ

is a function differentiable

V , their derivatives being bounded and differentiable functions. The first three

Newtonian theory of universal attraction

551

properties may easily be proved for particles

P in the exterior of the system S. If the

particle

P belongs to the interior of the system S, then that one becomes a singular

point (

), and we isolate it by a sphere containing it; the volume integral must be

calculated for the domain of volume

from which one subtracts the interior of that

sphere, while the surface integral (which appears by using a formula of Gauss-

Ostrogradskiĭ type) must be calculated for the sphere too. The integrands have no

singularities in this case, no matter how small is the radius of the sphere; then, this

radius is equated to zero.

Concerning the property iv), we denote

OQξ ==

JJG

ξ , (, )ϕ

) r ξ . From the

triangle

OPQ , it results (assuming that r is sufficiently great,

being bounded, we

may use a binomial expansion or a Maclaurin series)

(

)

11 1 1 1

2cos

Rrr

ξξψ

== = =

−

+−

JJJG

r ξ

(

)

(

)

1/2

()

1111

12cos (0) (cos)

rrr rn rr

ξξ ξ

ψψ

−

∞∞

⎡⎤

=+ − = =

⎢⎥

⎣⎦

∑∑

where

(cos )

P ψ are Legendre’s polynomials; we have

()

(cos ) (0)

ψ = , (0) 1

, (0) cos

′

(0) 3cos 1

′′

−

,...

Replacing in (9.1.8'), we get

(

)

11 1

() ()d cos ()d

UV V

μξψμ=+ +

∫∫∫ ∫∫∫

r ξξO ,

so that

()U r tends to zero as 1/r at infinity; observing that

()d

mVμ=

∫∫∫

ξ ,

()d

OC V

μ==

∫∫∫

JJG

ρξξ,

where

C is the centre of mass of the system S, we obtain the formula (9.1.11).

If, in particular, we choose the origin at the point

C , then we may write

(

)

() ()

UUr

==+

r O .

(9.1.12)

We may thus state that one obtains a sufficient good approximation by replacing the

mechanical system

S of attraction by its centre of mass C , at which we assume to be

concentrated the whole mass

m of the system (especially if the distance from the centre

of attraction

C to the particle P is sufficiently great). We show in the next subsection

that this result is rigorous if the mechanical system

S is with spherical symmetry.