Тевяшев А.Д., Литвин О.Г. Вища математика у прикладах та задачах. Ч 1
Подождите немного. Документ загружается.


§1.
Визначники
IV.
Задачі
для
практичних занять
У задачах
3.1-3.4
обчислити визначники другого порядку.
-14
а+Ь а-Ь
3.2.
52
а-Ь а+Ь
3.1.
3.3.
соза
-зіпа
зіпа соза
3.4.
2зіпфсозф 2зіп
ф-1
2
2С08
ф-1
2зІПфСОЗф
У задачах 3.5-3.6 розв'язати рівняння.
соз8х -зіп5х
3.5.
X
х +
1
-4
х +
1
=
0. 3.6.
8Іп8х соз5х
0.
У задачах
3.7-3.11
обчислити визначники третього порядку.
1
0
2 2 1 0 9
10 11
3.7.
0 2 0 .
3.8.
1
2
1 .
3.9.
1 1
1
2
0
3 0
1
2 2 3
4
3.10.
2
-2 1
3
4 2
-1
0 1
3.11.
2
3 4
1
2 5
4
1 6
У задачах
3.12-3.13
розв'язати рівняння:
3.12.
З
2
х
+ 2
х
-1
1
=
0.
3.13.
х
х+1 х+2
х+3
х+4 х+5
х+6
х+7 х+8
=
0.
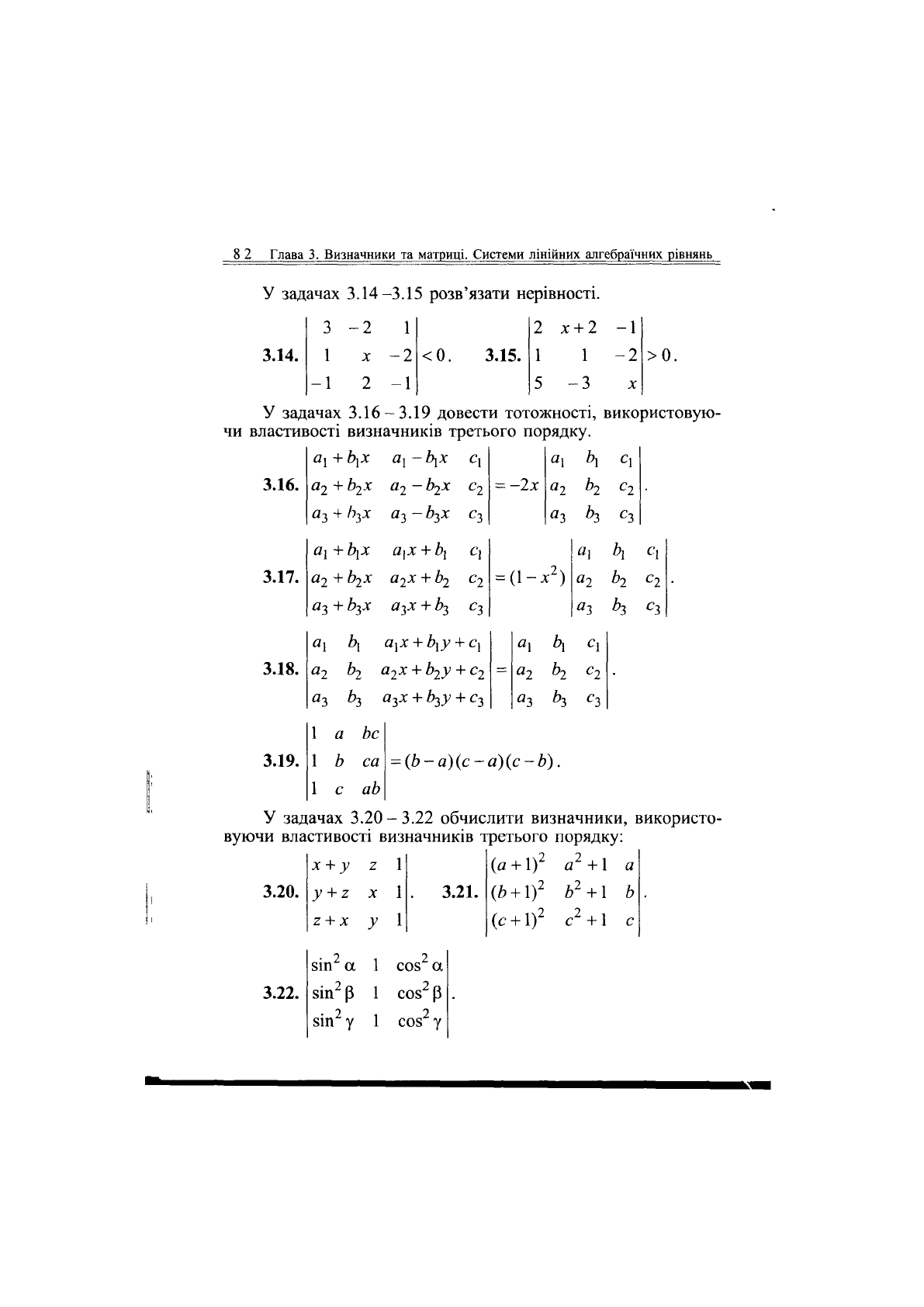
8
2 Глава 3. Визначники та матриці. Системи лінійних алгебраїчних рівнянь
У задачах 3.14-3.15 розв'язати нерівності.
3 -2
1
2 х
+
2 -1
3.14.
1
X
-2
<0.
3.15.
1 1
-2
>0
-1
2 -1
5 -3
X
У задачах 3.16-3.19 довести тотожності, використовую-
чи властивості визначників третього порядку.
«і
+ Ь\Х
сі\
-
}\х с
х
а
\
С\
3.16.
«2
+ Ь
2
х а
2
—
Ь
2
х с
2
-2х
а
2
Ь
2
с
2
«3
+ Ь
3
х
а
3
- Ь
3
х с
3
«3
Ь,
с
3
«1
+ Ь
1
х а
х
х +
Ь\
с
і
«1
С\
3.17.
а
2
+ Ь
2
х а
2
х + Ь
2
с
2
=
(\-х
2
)
а
2
Ь
2
с
2
а
3
+ Ь
3
х а
3
х + Ь
3
с
3
а
3
Ь
3
с
3
щ
Ьі
а
х
х + Ь\у + С]
а
\
Ьі
С\
3.18.
а
2
Ь
2
а
2
х + Ь
2
у + с
2
а
2
Ь
2
с
2
а
3
Ь
3
а
3
х + Ь
3
у + с
3
«3
Ь
3
с
3
1
а Ьс
3.19.
1
Ь са
= (*-а)(с-а)(
с-Ь).
1 с аЬ
У задачах 3.20 - 3.22 обчислити визначники, використо-
вуючи властивості визначників третього порядку:
ч2
х
+
у
2
1
3.20.
У
+
2
X
1 3
2
+ X
У
1
зіп
2
а 1
соз
2
а
3.22.
8іп
2
р
1
С08
2
(3
зіп
2
у
1
соз
2
у
3.21.
(а + іу
(Ь
+
\)
2
(с
+
1)
2
а
2
+\
Ь
2
+
1
с
2
+ 1
§1.
Визначники
83
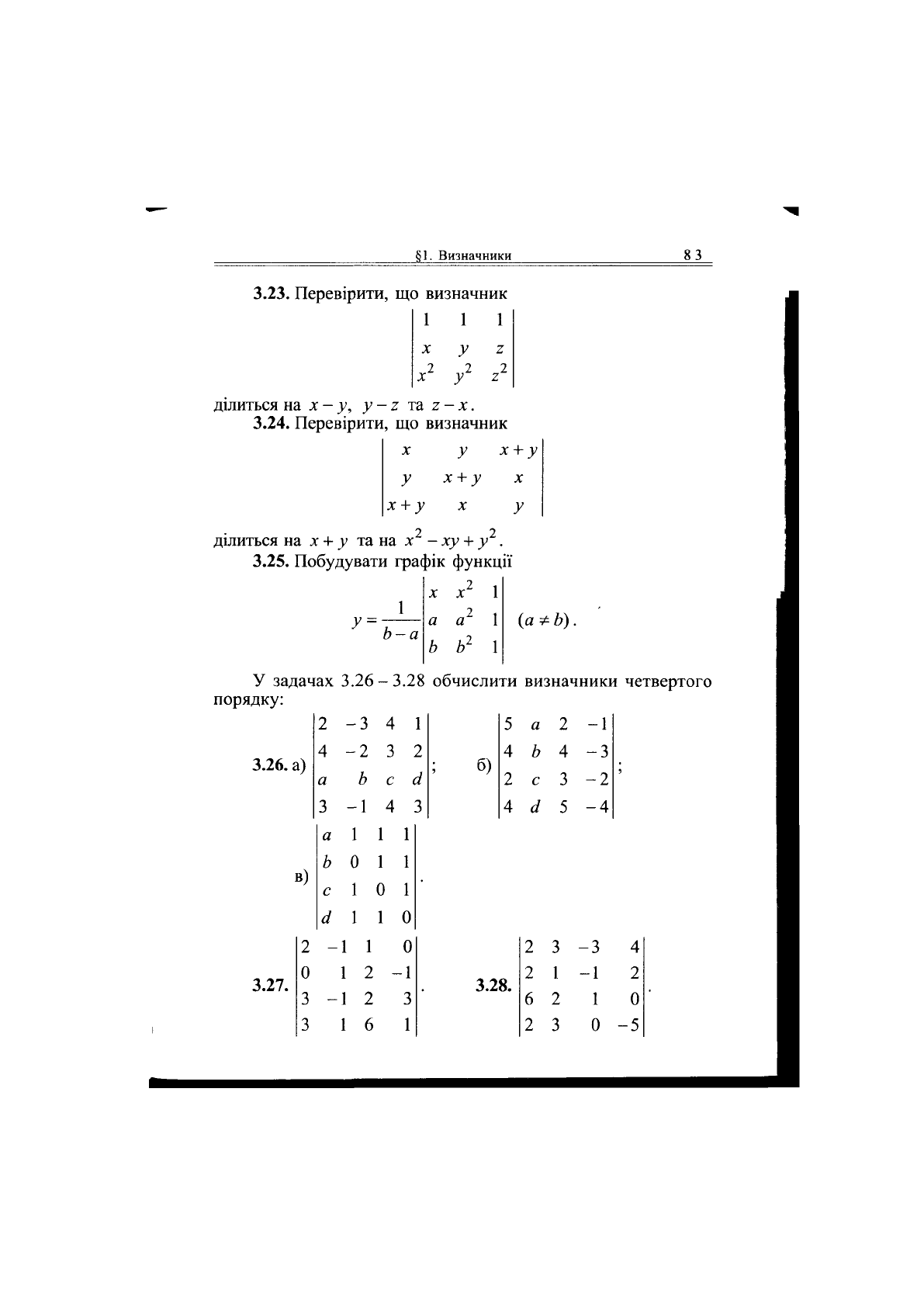
3.23.
Перевірити, що визначник
1 1 1
X
У
2
2 2 2
X
У
2
ділиться на х-у, у-2
та
2-х.
3.24.
Перевірити, що визначник
х у х + у
у х + у X
х + у х у
2 2
ділиться на х + у
та
на х - ху + у .
3.25. Побудувати графік функції
х г
2
1
У а а
Ь Ь
1
У задачах 3.26-3.28 обчислити визначники четвертого
порядку:
3.26. а)
-З
-2
Ь
-1
в)
3.27.
2
4
а
З
а
Ь
с
й
2 -1 1
0 1 2
3-12
3 1 6
4
З
с
4
б)
а
Ь
с
а
2
4
З
5
-1
-З
-2
-4
1 1 1
0 1 1
1 0 1
1 1 0
о
1
з
1
3.28.
2 3 -3 4
2 1 -1 2
6
2
1 0
2
3 0 -5

8 4 Глава 3. Визначники та матриці. Системи лінійних алгебраїчних рівнянь
У задачах 3.29 - 3.34 обчислити визначники, використовую-
чи теорему Лапласа.
3.29.
3.31.
0 - а -Ь
-а
а 0
- с
- е
Ь с 0
0
а
1
е 0
0
1 0 0
-1
-1 3 2 2
2 0 0 3
4
-2 3
1
3.30.
5 6 0 0 0
1 5 6 0 0
0 15 6 0
0 0 15 6
0 0 0 1 5
3.32.
-1
З
2
2
-1
З 1 1
0 0 0
1 3 2
0 0 0
0 0 0
2 1
1
1 1
X
0
-1
1
0
1 3 1 1 1
1 X -1
1
0
1 1 4 1 1
3.34.
1 0
х-1
0
1
1
1 1
5
1 0
1 -1 X 1
1
1 1 1 6
0 1 -1
0
X
3.33.
У задачах 3.35-3.36 обчислити визначники зведенням до
трикутного вигляду.
1
2 3 .
. п 3
2 2 . . 2
-1
0 3 .
. п 2
3 2 .
. 2
3.35. -1
-2 0 . . п
. 3.36.
2 2 3 .
. 2
-1
-2 -3 . . 0 2 2
2 .
. 3
3.37. Обчислити визначник, елементи якого задані умова-
ми ац = тіп (/',/).
3.38. Обчислити визначник, елементи якого задані умовами
а
ц
=тах(і,у)-

§2.
Матриці 85
У задачах 3.39-3.40 обчислити визначники п-го порядку
методом рекурентних співвідношень.
а еф 0 0
0
1 а +
р
ар ...
0 0
3.39.
0 1 а +
р
...
0 0
0 0 0 ...
1
а
+ Р
а +
р
ар 0
0
0
2 а +
р
ар
0
0
3.40.
0 1 а + р
0 0
0 0 0 1
а
+ Р
§2. Матриці
І. Короткі теоретичні відомості
Означення. Дії над матрицями. Матрицею розміру тхп називаєть-
ся таблиця чисел а
у
, і = 1,/я , у =
1,
л , вигляду
'«11 «12
«21 «22
А =
у
а
т\
«т2
Коротко:
А
тхп
,
(а
ц
)
тп
або (а
у
).
Якщо т=п , матриця називається квадратною порядку п .
Якщо всі елементи матриці дорівнюють нулю, матриця називається
нульовою. Позначення: О.
1
2п

V
<Г<3
(лава
У.
Шзначккш
та
матркдс.
Сїїстє&ґк лсксяккк
аягевржчнкк
(гсв(шг&
Квадратна матриця £) називається діагональною, якщо всі її елементи,
що не лежать на головній діагоналі, дорівнюють нулю, тобто
«11
о
0 «22
0 0
о
= с!іа§(а
1
ь «22
,...
,а
пп
).
Якщо діагональна матриця така, що всі а,-,- = 1,
і*
=
1,
л
,
то матриця нази-
вається одиничною. Позначення: Е . Таким чином,
(1 0 ... 0^
0 1 ... о
Е =
0 0
Матриця називається дійсною, якщо всі її елементи дійсні числа, в про-
тивному випадку, коли серед елементів є комплексні числа, матриця називаєть-
ся комплексною.
Сумою А + В матриць А=(а у)
тп
і В=(Ьу)
т п
називається матриця
с=
(
с
у)т,п
,така, що с
ц
- = ау
+
Ьу.
Добутком а А матриці А={а у)
тп
на число а називається матриця
С=(с,у)„,,„, така, що
Су=аау.
Добутком АВ матриці
А=(ау)
т
п
на В=(Ьу)
п
/ називається матриця
п
С
=(су)
т
і,
де
Сц
= ^а
ік
Ь
кі
, і=\,т , у =
1,/,
тобто елемент Су дорівнює
к=\
сумі добутків відповідних елементів / -го рядка матриці А і у -го стовпця мат-
риці В.
Мають місце такі властивості операцій над матрицями:
Г. А
+
В
=
В
+
А:
2
й
.
А
+
(В
+
С) = (А
+
В)
+
С;
3° (а + Р)Л = аЛ + рЛ; 4°. а(А
+
В)
=
аА
+
аВ;
6°.
А(ВС) = (АВ)С;
7". А(В
+
С) = АВ
+
АС .
Тут А , В , С - матриці, а, Р - числа.
Матриці А та В називаються переставними, якщо А В = В А
5° (ар)Л = афА);
і0

Степенем к матриці А називається матриця
С = А
к
=.А-А-...-А,
к раз
де к - ціле додатне число ; А
0
= Е.
Многочленом від матриці А називається вираз, що має вигляд
Р(А) =
а
0
А
к
+
а
х
А
к
'
х
+
а
2
А
к
'
2
+...
+
а
к
_
і
А
+
а
к
Е ,
де к - ціле додатне число, А
0
= Е.
Матриця, що отримана з даної матриці А заміною її рядків стовпця-
ми,
називається транспонованою до даної.
Позначення:
А'
або А'.
Мають місце властивості:
1°.
(А
Т
)
Т
=А; 2°. (А + В)
т
= А
т
+ В
т
; 3°. (АВ)
Т
=В
Т
А
Т
.
Приєднаною до квадратної матриці А називається матриця
(
А
\\ А
п
А
2
і
А
22
*л1
*п2
А
пп
)
А
\\ А
21
А\2
А
22
\А\„
Чп
А
п
\
Л
А
„2
А
П
п
)
де Ау - алгебраїчні доповнення елементів ау матриці А.
Квадратна матриця А називається невиродженою, якщо аеі А
Ф
0 .
Оберненою до квадратної матриці А називається матриця А~
х
така,
що АА"
Х
= А"
Х
А = Е.
Теорема. Для того щоб квадратна матриця А мала обернену, необ-
хідно та достатньо, щоб матриця А була невиродженою.
Метод приєднаної матриці для обернення матриць. Згідно з цим мето-
дом обернена матриця знаходиться за формулою
А~'
=•
аеіЛ
-А=-
аеіЛ
А
2
1
А
22
А ^
Т
Ч
2Я
\А
п
\
Ьі2
пп
у

8 8 Глава 3. Визначники та матриці. Системи лінійних алгебраїчних рівнянь
А,
А
'21
'12
А
'22
сІеіЛ
Обернені матриці мають такі властивості:
А,
ПП
)
1°.
(А-
Х
У
Х
=А;
2°
(А
Т
Т'=(А-
Х
)
Т
;
3°. (АВ)~
[
= В~
х
А~
х
.
Ранг матриці та його знаходження. Рангом матриці називається найви-
щий з порядків її мінорів, відмінних від нуля. Позначення К§ А .
Відмінний від нуля мінор матриці А
,
порядок якого г = Я§ А
,
називається
базисним мінором.
Теорема про базисний мінор. Базисні рядки матриці А лінійно не-
залежні. Будь-який рядок матриці А може бути представлений у вигляді
лінійної комбінації базисних рядків.
З теореми випливає, що максимальна кількість лінійно незалежних
рядків матриці дорівнює її рангу. Система рядків матриці, яка містить у
собі базисний мінор, утворює базис у системі рядків цієї матриці. Анало-
гічні твердження мають місце для стовпців.
Елементарні перетворення матриць:
1) перестановка рядків (стовпців);
2) множення рядка (стовпця) на число, відмінне від нуля;
3) додавання до елементів рядка (стовпця) відповідних елементів іншо-
го рядка (стовпця), помножених на деяке число.
Теорема. Елементарні перетворення не змінюють рангу матриці.
Основними методами обчислення рангу являються метод обвідних
мінорів та метод елементарних перетворень.
Метод обвідних мінорів обчислення рангу. Нехай в матриці знайдено
мінор к -го порядку М , відмінний від нуля. Розглянемо тільки ті мінори
(к + і)-го порядку, які містять у собі (обводять) мінор М . Якщо усі вони
дорівнюють нулю, то ранг матриці дорівнює к . В протилежному випадку
серед обвідних мінорів знайдеться ненульовий мінор (к + і)-го порядку, і
вся процедура повторюється.
Метод елементарних перетворень для знаходження рангу. Метод ба-
зується на теоремі про незмінність рангу при елементарних перетвореннях.
З допомогою елементарних перетворень дану матрицю А перетворюють у
матрицю В , ранг якої легко знаходиться. Тоді, К§ А = К§ В.
Матриці А
та
В, для яких Я§ А = К§ В називають еквівалентними: А~ В.

§2. Матриці
89
Метод елементарних перетворень для обернення матриць. Для заданої
матриці А п
-то
порядку будується прямокутна матриця Г
А
= (А
\
Е) роз-
міром п х 2л, приписуванням до А праворуч одиничної матриці. Далі, вико-
ристовуючи елементарні перетворення над рядками, матриця Г
А
зводиться
до вигляду (Е
|
В), що завжди можливо, якщо А невироджена. Тоді В = А~
]
.
Зауважимо, що метод елементарних перетворень для обернення мат-
риць має також назву метод Жордина - Гаусса або метод повного виклю-
чення. В методі повного виключення процес отримання оберненої матриці
формалізовано і весь процес представляється у вигляді деякої системи пра-
вил. Алгоритм методу і приклад розглянуто у §3 цієї глави.
Комплексні числа. Комплексним числом називається число вигляду
г = х
+
іу, (3.1)
де х,у - дійсні числа, / - уявна одиниця, причому і = -1.
Число х називається дійсною частиною, а у - уявною частиною
комплексного числа.
Два комплексних числа г
х
та г
2
називаються рівними, якщо рівні їх
дійсні та уявні частини.
Число г = х -
і
у називається спряженим до комплексного числа 2 .
Вигляд комплексного числа г = х +
і у
називають алгебраїчною фор-
мою комплексного числа.
Дії над комплексними числами у алгебраїчній формі виконуються
таким чином
2
Х
+2
2
=(х, + х
2
)+і(у
х
+у
2
);
г
\
~
2
2 = (*] -
х
г)+і{у\ -Уг)\
г
Х
2
2
= (х
х
+іу
х
)(х
2
+іу
2
)={х
х
х
2
-у
х
у
2
)+
і(
х
]У2
+>'і*2);
£і_
=
2
1 '^2
=
*1*2 + У\У2
+ І
Х
2У\ -
Х
\У2
2
2
2
2
-І
2
ХІ+уІ
Х
2+У2
Кожному комплексному числу 2 = х + іу може бути поставлена у
відповідність точка М(х, у) у декартовій прямокутній системі координат.
уА

9 0 Глава 3. Визначники та матриці. Системи лінійних алгебраїчних рівнянь
Модулем комплексного числа називається число |г| = Г = -^ґ
2
+ у
2
.
~
х
• У
ОчЄВИДНО,
ЩО
СОЗ
ф = — , 8111 ф = — .
Г
Г
Число ф називається аргументом комплексного числа. Враховуючи, що
х = гсо8ф, 7 = г8Іпф, комплексне число (3.1) представляється у вигляді
г = г(со8ф + /зіпф), (3.2)
який називається тригонометричною формою комплексного числа.
Дії над комплексними числами, заданими у тригонометричній формі ви-
конуються так:
2,
г
2
=,} г
г
[сов (ф,
+ ф
2
) + і
8ІП (ф,
+ ф
2
)];
-і-
= -Цсо8(ф, -ф
2
) +
/8іп(фі
-ф
2
)];
2
2
Г
2
2
п
= г" (соз «ф + /зіп пф) - формула Муавра;
пГ
пГ (
<р
+ 2кк . . ф + 2£лЛ --
<]2=Щг
соз- +
гзіп-
, к =
0,п-\.
Комплексні матриці. Деякі типи матриць. Нехай С = {
с
к/}
т
„ -комплексна
матриця. Тоді = + іЬщ V к,
у .
Тобто С = А + іВ,де А
та
В - дійсні мат-
риці: А - (а^ ] , В = (й
І7
) ;
У4
- дійсна, 5 - уявна частина матриці С.
Матриця С
—
А-іВ називається комплексно-спряженою до матриці С .
Матриця С
т
=С* називається спряженою до матриці С .
У таблиці 3.1 наведено важливі типи квадратних матриць як для ви-
падку, коли матриця А - дійсна, так і для випадку, коли матриця А - ком-
плексна. Ці типи матриць будуть використані в подальшому у гл. 5.
Таблиця 3.1
Номер
типу
Матриця А - дійсна
Номер
типу
Матриця А - комплексна
1. Симетрична матриця:
А
= А
Т
(а
ц
=а„ V/,./)
1.
Ермітова матриця
А
= А* (я,у =а
л
У/,у)
2.
Кососиметрична матриця:
А
= ~А
Т
(й
у
=-а
р
У і,])
2.
Косоермітова матриця
А
= -А* {ау =-а
7
-,- У і, у)
3.
Ортогональна матриця:
АА
Т
=А
Т
А
= Е (л
г
=/Г')
3.
Унітарна матриця
АА* = А*А = Е (а'=А~
}
)
